文章目录
好,大家请坐下,我要问一个问题,懂我 80% 英文的请举手 ,远不到一半,接下来多半讲中文,再逐步增加使用英文的比例。
!NOTE
此处部分内容省略,主要是第一讲的复习与强化;下文中杨老授课中将中英文混杂在一起,由于音频整体为 AI 转录,存在将中文转录为英文的情况,后翻译为中文。
此外,由于原视频示意图存在被水印遮挡干扰以及清晰度问题,大部分示意图我通过 Excalidraw 画板重新手绘制作,并尽量接近杨老手绘原图,但可能存在细节缺失。
加速度
Now we go to uniform or constant acceleration. Acceleration is acceleration. We have to ask what acceleration is. Acceleration means that if a person goes from this point to this point, he will have an instantaneous velocity at every point. (现在我们转向匀加速或恒加速。Acceleration 就是加速度。我们必须先问加速度是什么。加速度意味着,如果一个人从这一点移动到另一点,他在每一点都有一个瞬时速度。但这个速度不一定是一样的。)
For example, if a ball falls from the top to the bottom, we all know that it moves faster and faster. In the process of falling from the top to the bottom, its velocity is different at every point. It is getting faster and faster.(例如,如果一个球从顶部落到底部,我们都知道它会越来越快。在从顶部落到底部的过程中,它在每一点的速度都是不同的。它变得越来越快。)
So I can ask, for example, what is the average velocity between the height of the ground and the height of the ground? What is its average velocity? It has a velocity. It has an average velocity. We already have the concept of average velocity and instantaneous velocity.(所以我可以问,比如说,在离地面 1 尺高的地方和地面之间的平均速度是多少?我们已经有了平均速度和瞬时速度的概念。)
But if I draw it now, this side is x, this side is t. For example, this is t, one second, two seconds, three seconds. This is one meter, two meters, three meters. If there is a line, it is a straight line.(但如果我现在画出来,这边是 x x x,这边是 t t t。例如,这是 t t t,一秒、两秒、三秒。这是一米、两米、三米。如果有一条线,那就是一条直线。)
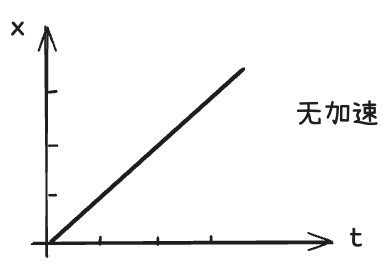
Can you tell me what are the characteristics of such a movement? It has a fixed instantaneous velocity. Why? Because it moves one meter in the first second, one meter in the second second, and one meter in the third second. So its movement is uniform.(你能告诉我这种运动有什么特点吗?它有一个固定的瞬时速度。为什么?因为它在第一秒移动一米,第二秒移动一米,第三秒移动一米。所以它的运动是匀速的。)
In other words, it has no acceleration. Such a movement has no acceleration. What kind of movement has acceleration? It moves faster and faster. So, for example, such a movement has acceleration. Why? Because it moves only a little distance in the first second. In the second second, it moves from here to here.(换句话说,它没有加速度。这样的运动没有加速度。什么样的运动有加速度呢?运动速度越来越快。例如,这样的运动就有加速度(抛物线曲线)。为什么?因为它在第一秒内只移动了一小段距离。在第二秒内,它从这里移动到这里。)
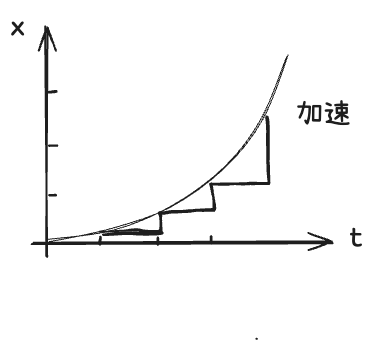
In the third second, it moves from here to here. In the second second, it moves from here to here. In the third second, it moves from here to here. So its speed is getting faster and faster. So this is an acceleration. This kind of acceleration is called concave upwards.(第三秒时,它从这里移动到这里。第二秒时,它从这里移动到这里。第三秒时,它从这里移动到这里。所以它的速度越来越快。这是一种加速运动。这种加速被称为向上凹。)
Concave upwards. If it is like this, this is called concave downwards. If you move it like this every second, you will see that it moves in the first second, in the second second, in the third second, and in the fourth second.(向上凹。如果是这样,这就叫做向下凹。如果你每秒这样移动它,你会看到它在第一秒、第二秒、第三秒和第四秒移动。)
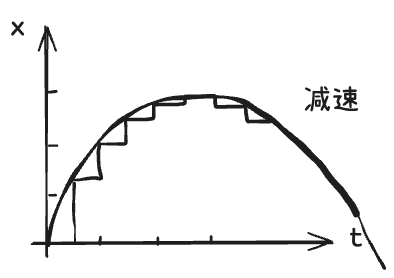
It moves less and less. So its speed is decreasing. So, if you draw a line like this, if it is concave upwards, it is an acceleration movement. If it is concave downwards, it is a deceleration movement. You have to pay attention to this. If you extend it like this, if you extend it like this, it doesn't move at all.(它移动得越来越少。所以它的速度在降低。因此,如果你这样画一条线,如果它是向上凹的,那就是加速运动。如果它是向下凹的,那就是减速运动。你必须注意这一点。如果你这样延伸它,如果你这样延伸它,它根本不动。)
If you extend it like this, it moves downwards. If you extend it like this, This is still a deceleration movement. But its speed is increasing. It moves one meter per second. Then it moves half a meter per second. Then it moves a quarter of a meter per second.(如果你这样伸展它,它会向下移动。如果你这样伸展它,这仍然是一个减速运动。但它的速度在增加。它每秒移动一米。然后每秒移动半米。接着每秒移动四分之一米。)
After a few seconds, it doesn't move at all. It doesn't move at all. It doesn't move at all. If you extend it downwards, its speed becomes negative. This is a deceleration movement. Decreasing velocity.(几秒钟后,它完全不动了。完全不动了。完全不动了。如果你向下延伸它,它的速度会变成负数。这是一种减速运动。速度在减小。)
Decreasing velocity is not only positive, it can also be negative. So, if you throw a ball, and it falls down, its speed goes downwards. Then it becomes more and more powerful. When it goes upwards, if you extend it downwards, I have introduced a new concept to you. The speed can be positive or negative. If I extend it outwards, extend it inwards, if I throw a ball, it will go upwards.(速度的减小不仅可以是正向的,也可以是负向的。所以,如果你扔一个球,球下落时,它的速度是向下的。然后它会变得越来越快。当球向上运动时,如果你向下延伸,我就向你介绍了一个新概念。速度可以是正的也可以是负的。如果我扔一个球,它就会向上运动。)
In the beginning, dy dt is one meter per second. Obviously, it is getting slower and slower. So the picture is like this. We will discuss this in the future.(一开始, d y / d t \mathrm{d}y/\mathrm{d}t dy/dt 是每秒一米。显然,它变得越来越慢。所以图像是这样的。我们以后会讨论这个问题。)
加速运动的位移、速度、加速度曲线示意图
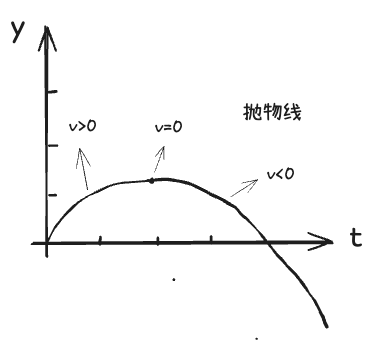
Do you know this line? This Y, a ball is thrown up. This is T. Do you know what is the name of this line? It is called the bubble line. Parabola. We will talk about this later. So I want to tell you that when it is here, its speed is positive. Its dx dt is positive.(你知道这条线吗?这个 y y y 轴,一个球被抛上去。这是 t t t 轴。你知道这条线的名字吗?它被称为抛物线。我们稍后会讨论这个。所以我想告诉你,当它在这里时,它的速度是正的。它的 d x / d t \mathrm{d}x/\mathrm{d}t dx/dt 是正的。)
At this point, its dx dt is zero. At this point, its dx dt is negative. Its instantaneous speed is positive here. It is zero here. It is negative here. Actually, you can understand it at a glance. When it goes up, its instantaneous speed is positive. At this point, when it is flat, its instantaneous speed is zero. At this point, its instantaneous speed is negative.(此时,它的 d x / d t \mathrm{d}x/\mathrm{d}t dx/dt 为零。此时,它的 d x / d t \mathrm{d}x/\mathrm{d}t dx/dt 为负。在这里,它的瞬时速度为正。在这里为零。在这里为负。实际上,你一眼就能明白。当它上升时,瞬时速度为正。在这一点上,当它是平的时,瞬时速度为零。在这一点上,它的瞬时速度为负。)
You must be able to understand it to a degree that you know it at a glance. If I don't plot Y now, I plot its speed, its dy dt. Its instantaneous speed. Its instantaneous speed, its dy dt, is one. At t equals zero, at t equals zero, its speed is one meter per second. But later on, it goes slower and slower.(你必须达到一眼就能理解的程度。如果我现在不画 y y y,而是画它的速度,即 d y / d t \mathrm{d}y/\mathrm{d}t dy/dt。它开始的速度, d y / d t = 1 \mathrm{d}y/\mathrm{d}t=1 dy/dt=1。在 t = 0 t=0 t=0 时,它的速度是每秒 1 米。但之后,它会越来越慢。)
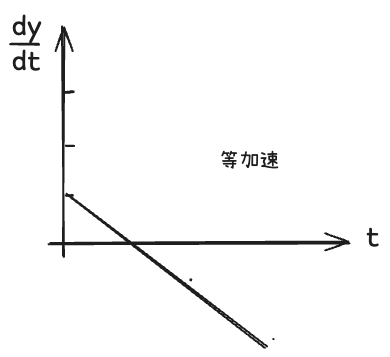
At this point, its speed becomes zero. From this point to this point, it goes slower and slower. If you want to plot it, it is like this. If you throw something away, its dy dt is a straight line. This is called constant acceleration. What is constant acceleration? At each point, there is a position.(此时,它的速度变为零。从这一点到这一点,它变得越来越慢。如果你想绘制它,它看起来是这样的。如果你扔出某物,它的 d y / d t \mathrm{d}y/\mathrm{d}t dy/dt 是一条直线。这被称为恒定加速度。什么是恒定加速度?在每一个点上都有一个位置。)
This is the position. This is the speed. The one below is acceleration. The relation between speed and position is that speed is dy dt. The relation between acceleration and speed is that acceleration is dy dt. Speed is the derivative of position.(这是位置。这是速度。下面的是加速度。速度与位置的关系是速度等于 d y / d t \mathrm{d}y/\mathrm{d}t dy/dt。加速度与速度的关系是加速度等于 d 2 y / d t 2 \mathrm{d}^2y/ \mathrm{d}t^2 d2y/dt2。速度是位置的导数。)
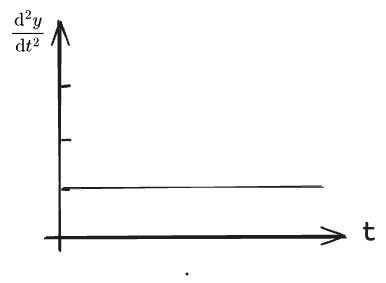
Acceleration is the derivative of speed. Does everyone understand this? Yes. Is there anyone who doesn't understand? If you have a little problem with this, after the class, find a student who understands and explain it to you.(加速度是速度的导数。大家都明白了吗?明白了。有没有人不明白?如果你对这一点有点问题,下课后找一个明白的同学给你解释一下。)
This is the most basic concept. You have to become intuitive with this concept. At each point, its instantaneous velocity is dy dt. In fact, what I am telling you now is the most basic concept of calculus. If this motion is like this, at this point, its velocity is between this point and this point. What is its average velocity? Okay.(这是最基本的概念。你必须对这个概念有直觉性的理解。在每一点上,它的瞬时速度是 d y / d t \mathrm{d}y/\mathrm{d}t dy/dt。实际上,我现在告诉你的正是微积分中最基本的概念。如果运动是这样的,在这个点上,它的速度介于这个点和这个点之间。那么它的平均速度是多少呢?好的。)
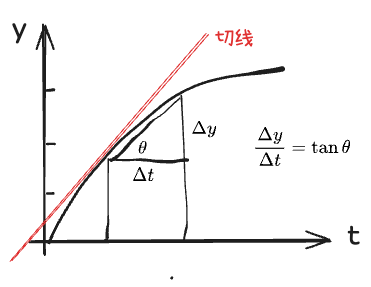
This is delta t. This is delta x. At this point, it is delta y. From here to here, the time is delta t because this is t. If it goes up, this is delta y. So its average velocity is delta y divided by delta t. What does this mean? If I draw a straight line here and it becomes a triangle. This triangle has this angle. This angle is called theta.(这是 Δ t \Delta t Δt。在这一点上,它是 Δ y \Delta y Δy。从这里到这里,时间是 Δ t \Delta t Δt,因为这是 t t t。如果它上升,这就是 Δ y \Delta y Δy。所以它的平均速度是 Δ y \Delta y Δy 除以 Δ t \Delta t Δt。这是什么意思?如果我在这里画一条直线,它就变成了一个三角形。这个三角形有这个角度。这个角度叫做 θ \theta θ。)
This straight triangle, this side is delta y, this side is delta t. This angle is theta. So what is the relationship between delta y and delta t? What is the relationship with theta? It is tangent. This is what you learned in the triangle.(这个直角三角形,这条边是 Δ y \Delta y Δy,这条边是 Δ t \Delta t Δt。这个角是 θ \theta θ。那么 Δ y \Delta y Δy 和 Δ t \Delta t Δt 之间的关系是什么?与 θ \theta θ 的关系又是什么?是正切。这就是你在三角形中学到的内容。)
So if you draw a straight line, this angle is tangent theta. Okay. If I don't move this point and reduce this delta t, if I reduce it, I can't draw it clearly. The triangle is enlarged. If I reduce it, for example, if delta t is half, then it comes here. So it becomes like this.(所以如果你画一条直线,这个角度就是 tan θ \tan\theta tanθ。好的。如果我不移动这个点,减小这个 Δ t \Delta t Δt,如果我减小它,我无法清晰地画出来。三角形被放大了。如果我减小它,比如 Δ t \Delta t Δt 减半,那么它就会到这里。所以它变成这样。)
If I try my best to reduce it to the end, I am asking a question. What does this line become? It is called tangent. What does tangent mean? If you draw this line, the further you go, the closer it becomes.(如果我尽力把它简化到最后,我在问一个问题。这条线会变成什么?它被称为切线。切线是什么意思?如果你画这条线,走得越远,它就越接近。)
In the end, it becomes a tangent. So what is the limit of this? So, dy dt is equal to what? It is equal to tangent of which angle? It is the tangent of which angle? It is the tangent of which angle? Because theta becomes the tangent. This concept, tangent of which angle and the t-axis, the whole tangent is called slope.(最终,它变成了一条切线。那么这个的极限是什么?所以, d y / d t \mathrm{d}y/\mathrm{d}t dy/dt 等于什么?它等于哪个角的正切?因为 θ \theta θ 变成了切线。这个概念,哪个角的正切与 t t t 轴,整个切线被称为斜率。)
d y d t = tan ( 切线与 t 轴之间的夹角 ) \frac{\mathrm{d}y}{\mathrm{d}t}=\tan(\text{切线与 t 轴之间的夹角}) dtdy=tan(切线与 t 轴之间的夹角)
Why is it called slope? What does slope mean? Is it the slope? What is it in Chinese? Is it called slope? I use the word slope. If you go up a slope, that slope is called slope. The word slope in the order is tangent.(为什么叫斜率?斜率是什么意思?是那个坡吗?中文叫什么?我用slope这个词。如果你上一个坡,那个坡就叫 slope。数学里的 slope 这个词是切线。)
So if you see a line, draw this line, there is a curve at that point. The curve is the direction it is going at that time. The tangent between the t-axis and the curve is the derivative at that point. After you understand this, you will know that the movement is here. Because its theta is 20 degrees. If you go here, the theta becomes smaller, so the tangent becomes smaller.(所以如果你看到一条线,就画这条线,那里有一个曲线。这个曲线就是它当时的方向。 t t t 轴和曲线之间的切线就是该点的导数。理解了这一点,你就会知道运动在这里。因为它的 θ \theta θ 角是 20 度。如果你到这里, θ \theta θ 角变小,所以切线也变小。)
If you go here, the tangent is like this. If the tangent is like this, the theta becomes zero. So the tangent of theta is zero. So at this point, the slope is zero. At this point, the slope becomes negative. Because the angle is going to the bottom.(如果你走到这里,切线的方向是这样的。如果切线是这样的,那么 θ \theta θ 角就变成了零。因此, θ \theta θ 的正切值为零。所以在这一点的斜率为零。而在这一点,斜率变为负值。因为角度开始向下倾斜。)
So the theta becomes negative. So in fact, the concept of derivative is very simple. If there is a curve, the slope goes up at this point, so it is positive. Its slope is positive. At this point, the slope is zero. At this point, the slope is negative. At this point, the slope is zero. This slope is positive. This slope is zero. It is negative. It is zero. And so on.(所以 θ \theta θ 就变成了负值。实际上,导数的概念非常简单。如果有一条曲线,在某一点的斜率上升,那么它就是正的。它的斜率是正的。在这一点,斜率为零。在这一点,斜率为负。在这一点,斜率为零。这个斜率是正的。这个斜率为零。它是负的。它是零。以此类推。)
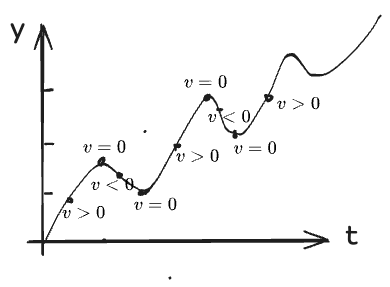
So you understand this. So this is the picture of location. The picture of location versus time. This is its speed. So the speed at this point is positive. So it is positive. At this point, the speed is zero. At this point, the speed becomes negative. So dy dt is the slope of this thing. The slope of this thing is always the same. Because its tangent is always in the same direction. So dy dt is a negative number. And it is a fixed number. So it does not change for time. So the acceleration is this picture.(所以你明白这一点。这是位置随时间变化的图像。这是它的速度。在这个点上,速度是正的。所以它是正的。在这个点上,速度为零。在这个点上,速度变为负的。 d y / d t \mathrm{d}y/\mathrm{d}t dy/dt 就是这条线的斜率。这条线的斜率始终相同。因为它的切线始终在同一方向上。所以 d y / d t \mathrm{d}y/\mathrm{d}t dy/dt 是一个负数。而且它是一个固定的数字。所以它不随时间变化。加速度就是这个图像。)
Do you understand the three pictures I just mentioned? If you don't understand this, I suggest that you find a classmate who will definitely understand. Before Galileo, everyone was not clear about the speed of a falling object. Why was it not clear at that time? For example, everyone knows that Galileo put down two things from the top of the Pisa tower.(我刚才提到的三张图你明白了吗?如果你不明白这个,我建议你找一个肯定明白的同学。在伽利略之前,大家对物体下落的速度都不清楚。为什么当时不清楚呢?比如说,大家都知道伽利略从比萨斜塔上放下两样东西。)
One is heavy and the other is light. This is true. So you have to ask if the two things fall to the bottom at the same time. So before that, I think everyone outside China has an impression that the heavy object falls to the ground first and the light object falls to the ground later. It proves that it is not true. The two things fall to the ground at the same time.(一个重,一个轻。这是事实。所以你要问这两样东西是否会同时落地。在此之前,我想中外的所有人都有一种印象,即重的物体先落地,轻的物体后落地。事实证明并非如此。两样东西会同时落地。)
So why did it have a wrong impression before? Someone will answer this question. No. Why did you have an impression that the heavy object fell to the ground first and the light object fell to the ground later? Because of the resistance of the air.(那么为什么之前会有错误的印象呢?有人会回答这个问题。不。为什么你会觉得重的物体先落地,轻的物体后落地?因为空气的阻力。)
Because of the resistance of the air, if you use a very light object, if you use a very light balloon, it will fall very slowly. So of course it will fall to the ground later. So in the past, we didn't know the effect of the resistance of the air.(由于空气阻力的存在,如果你用一个非常轻的物体,比如一个很轻的气球,它会下落得非常缓慢。因此,它当然会更晚落到地面。所以过去我们并不知道空气阻力的影响。)
What Galileo did was that he used two different weights but they were both quite heavy. So the resistance of the air was not an important factor in his experiment. In this case, he proved that the two things fell to the ground at the same time.(伽利略所做的就是使用两个不同但都很重的重量。因此,空气阻力在他的实验中并不是一个重要因素。在这种情况下,他证明了两样东西同时落地。)
So he proved that if the resistance of the air was not important, the object that fell to the ground would look like this. If you draw it as a position, it would be a parabola. If you draw it as a speed, it would be a constant speed.(所以他证明了,如果空气阻力不重要,那么落向地面的物体看起来会是这样。如果画成位置图,就是一条抛物线。如果画成速度图,就是匀速运动。)
If you draw it as an acceleration, the acceleration would be a constant negative number. This was discovered only after Galileo. Today, of course, it is very easy to do this experiment. Because at that time, measuring time was quite complicated. Usually, if you want to put a ball on the ground, it will fall to the ground in a very short time, so it is very difficult to measure. Today, with a very simple method, you can measure it very accurately and you will know that the acceleration is indeed a constant.(如果你把它画成加速度,加速度将是一个恒定的负数。这是在伽利略之后才被发现的。当然,今天做这个实验非常容易。因为在那时,测量时间相当复杂。通常,如果你想将一个球放在地上,它会在极短的时间内落到地面,所以很难测量。如今,用一个非常简单的方法,你就可以非常精确地测量它,并且你会知道加速度确实是一个常数。加速度的数目,你得看书并记住这个数字。因为这个数字非常重要。)
匀加速运动(重要公式)
Below, I want to talk about the rate, the rate of acceleration. We need to discuss the rate of acceleration. Uniform acceleration motion. If at the beginning, its speed is V0, original velocity.But, uniform acceleration means that for every unit of time, the velocity is increased by a certain amount, a. a is equal to uniform acceleration. Uniform means that it is uniform. Okay.(接下来,我想谈谈等加速,我们需要讨论匀加速运动。如果开始时,它的速度是 v 0 v_0 v0,即初速度。但是,匀加速意味着在每单位时间内,速度都会增加一定的量,即 a a a。 a a a 等于匀加速度。"匀"意味着它是均匀的。好的。)
Now, if the original velocity is V0, what is the velocity after one second? What is the velocity after two seconds? Therefore, the velocity after T seconds is, you might say that is the definition. This is the definition of uniform acceleration motion. That is to say, the original velocity is V0, the final velocity is V, the final velocity is V, then the final velocity is equal to V0 plus a times T. This is the, you might say this is the definition of uniform motion.(现在,如果初速度为 v 0 v_0 v0,那么一秒后的速度是多少?两秒后的速度又是多少?因此, t t t 秒后的速度,你可以说这就是定义。这就是匀加速运动的定义。也就是说,初速度为 v 0 v_0 v0,末速度为 v v v,那么末速度等于 v 0 + a t v_0+at v0+at。这就是,你可以说这就是匀速运动的定义。)
v = v 0 + a t v=v_{0} + at v=v0+at
Okay. Do we know what is the distance traveled? What is the distance traveled in T? The distance traveled is X. I will not talk about Y now. I will talk about X. X minus X0. X0 is the original position. X is the later position. So X minus X0 is the distance traveled during the period P. This is easy to calculate because the initial velocity is V0.(好的。我们是否知道行驶的距离是多少?在时间 t t t 内行驶的距离是多少?行驶的距离是 x x x。我现在不会谈论 y y y。我要谈论的是 x x x。 x − x 0 x-x_0 x−x0, x 0 x_{0} x0 是初始位置。 x x x 是后来的位置。所以 x − x 0 x-x_0 x−x0 就是在时间段 t t t 内行驶的距离。这很容易计算,因为初始速度是 v 0 v_{0} v0。)
Final velocity is V0 plus a times T. This is initial velocity. This is final velocity. So what is the average velocity? Average velocity is the average of these two numbers. So it's V0 plus V0 plus a times T divided by two. That's average velocity. Average velocity times the time is the distance traveled.(末速度等于初速度 v 0 v_{0} v0 加上加速度 a a a 乘以时间 t t t。这是初速度,这是末速度。那么平均速度是多少呢?平均速度就是这两个数的平均值。所以它是 v 0 v_{0} v0 再加上 a a a 乘以 t t t,然后除以二。这就是平均速度。平均速度乘以时间等于行驶的距离。)
x − x 0 = v 0 + v 0 + a t 2 t = v 0 t + 1 2 a t 2 x-x_{0}=\frac{v_{0}+v_{0}+at}{2}t=v_{0}t+\frac{1}{2}at^2 x−x0=2v0+v0+att=v0t+21at2
Therefore, the distance traveled is equal to T times this quantity, which therefore is equal to... Does everybody understand what we just did? So now there are two important formulas. This is one formula. This is another formula.(因此,行驶的距离等于 t 乘以这个量,因此等于......大家都明白我们刚才做了什么吗?所以现在有两个重要的公式。这是一个公式。这是另一个公式。)
This formula gives you the final velocity. This formula gives you the distance traveled. This may sound very simple, but actually we have made an assumption. The assumption is that it's a uniform acceleration. If it were not a uniform acceleration, this average velocity calculation is not correct. The reason that... No, the average velocity is always this.(这个公式给出了最终速度。这个公式给出了行进距离。这听起来可能很简单,但实际上我们做了一个假设。这个假设是加速度是均匀的。如果加速度不均匀,这个平均速度的计算就不正确。原因是......不,平均速度总是这样。)
The average velocity is always equal to... The average velocity... Can somebody tell me? If it were not a uniform acceleration, which step I just mentioned is incorrect? OK, let's review. If it were not a uniform velocity, and not a uniform acceleration, then this formula is incorrect. Because this formula is the definition of a uniform acceleration.(平均速度总是等于...平均速度...有人能告诉我吗?如果不是匀加速运动,我刚才提到的哪一步是错误的?好,我们来回顾一下。如果不是匀速运动,那么这个公式就是错误的。因为这个公式是匀加速运动的定义。)
(上面的公式都要求 a a a 是固定的,否则末速度和平均速度的计算都不对)
So this formula is incorrect from the beginning. And this formula is also incorrect. But the spirit of this formula says that the initial velocity plus the final velocity is divided by 2, which is the average velocity. Is this correct? Who agrees that it's correct? Who disagrees that it's incorrect? It's incorrect. It's incorrect. Because... Anyway, if you think it's incorrect, then it's correct. Because it's a uniform acceleration, that's why it's correct. That's why there is this formula. OK.(所以这个公式从一开始就是错的。这个公式也是错的。但这个公式的精神是说初速度加末速度除以 2,就是平均速度。这个对吗?谁同意这是对的?谁不同意这是错的?这是错的。这是错的。因为......总之,如果你觉得这是错的,那它就是对的。因为是匀加速运动,所以它是对的。所以才有这个公式。好吧。)
OK. For the following questions, so that you know whether you understand or not, I will give you a question. This question is... Use these two formulas. There are two formulas in the square. Use these two formulas to prove. Prove that it's V2 minus V02.(好的。接下来的问题是为了确认你是否理解,我会给你一个问题。这个问题是...使用这两个公式。方框中有两个公式。用这两个公式来证明。证明它是 v 2 − v 0 2 v^2-v_0^2 v2−v02。)
v 2 − v 0 2 = 2 a ( x − x 0 ) x − x 0 = v t − 1 2 a t 2 v^2-v_{0}^2=2a(x-x_{0}) \quad\quad\quad x-x_{0} = vt-\frac{1}{2}at^2 v2−v02=2a(x−x0)x−x0=vt−21at2
With these two formulas, it's easy for you to prove this. You don't need to teach this topic. But if you do this exercise, you would understand the thing better. I think we are going faster than I originally thought we would go. So I will see whether you... The exercises that you are going to handle next Monday. Prove that you have no problem.(有了这两个公式,你很容易就能证明这一点。这部分内容不需要专门讲解。但如果你做这个练习,你会更好地理解这个问题。我觉得我们的进度比我原先预想的要快。所以我要看看你是否...下周一你要处理的练习题。证明你没问题。)
If the exercise next Monday is not good, then we have to find another way. If it's good, then I think we can continue at this speed. In fact, there is little content in this book. If you know the source of the two formulas I just mentioned, and you know how to apply them, then you basically know everything in the second chapter. As I said before, at the end of every chapter, there is a review and summary. You should take a look at the review and summary.(如果下周一练习效果不佳,我们就得另寻他法。如果效果理想,我认为可以继续保持这个进度。其实这本书内容并不多,只要掌握我刚才提到的两个公式的来源和应用方法,第二章的内容就基本掌握了。正如我之前所说,每章末尾都有复习总结部分,你们应该好好看看这些复习总结。)
If you want to know if you fully understand that chapter, you should take a look at the review and summary. I hope as time goes on, you will understand my English better and better. As I said, these days English becomes a sort of an international language for science. So it would be very important for you to brush up your English as fast as possible. I have my office hours on the syllabus. Professor Ruan and Professor An also have their office hours. So if you have any questions, you can come to us. Okay, good luck. (如果你想确认自己是否完全理解了那一章的内容,应该看看复习和总结部分。我希望随着时间的推移,你会越来越理解我的英语表达。正如我所说,如今英语已成为科学界的国际通用语言。因此,尽快提高你的英语水平对你来说非常重要。我的办公时间在教学大纲上。阮教授和安教授也有他们的办公时间。所以如果你有任何问题,都可以来找我们。好的,祝你好运。)