下面我们专注于麦克斯韦方程组，尝试找到散度和旋度后面的东西。
已知麦克斯韦方程组的四个方程，
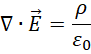
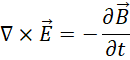
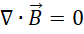
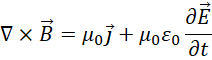
前后两对各自合成为del算子对函数应用的形式，
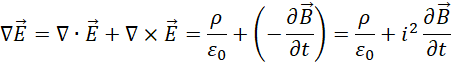
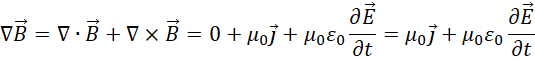
根据两个方程的对称性，对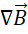 
进行重新组合（数学方法，不代表物理上的可验证性），
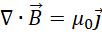
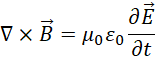
考虑，
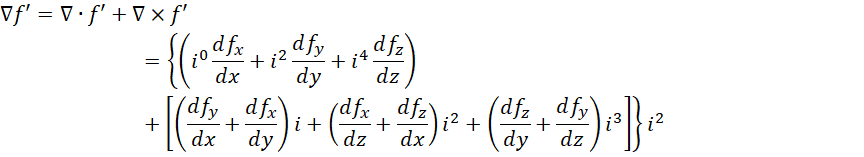
应用于，
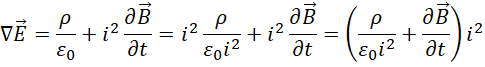
在三维空间，
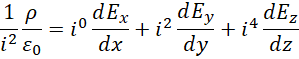
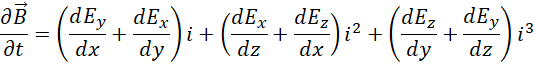
再应用于，
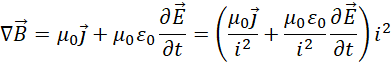
在三维空间，
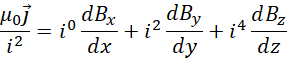
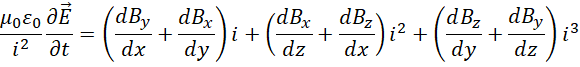
假定（后面会验证其正确性），
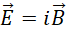
也就是，
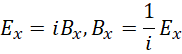
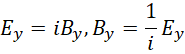
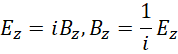
代入散度，
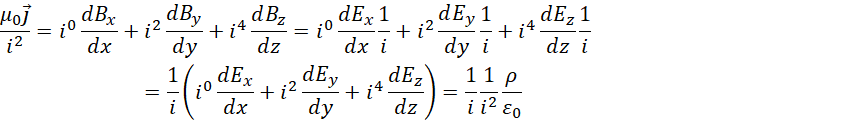
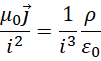
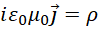
代入旋度，
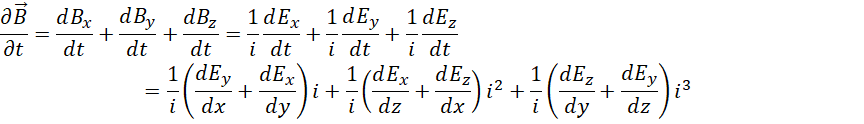
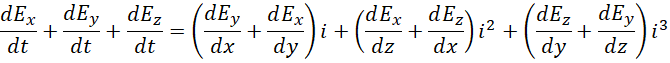
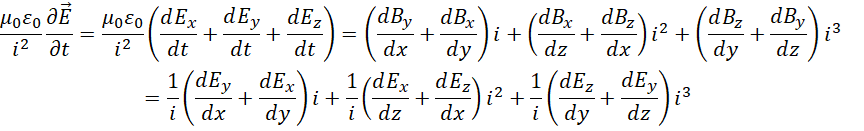
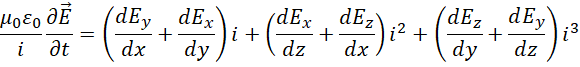
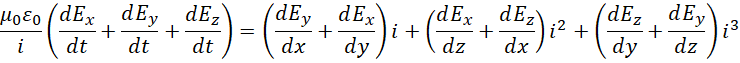
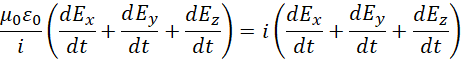
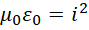
配合，
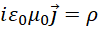
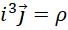
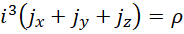
假定，
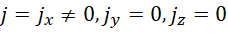
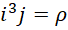
其中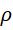 
为电荷密度，也就是单位体积中的电量， 
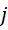为电流密度，也就是单位面积上流过的电流，
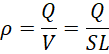
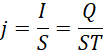
所以，
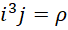
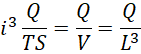
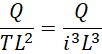
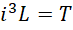
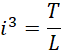
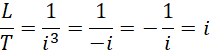
我们最初假定，
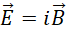
得到，
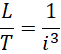
所以，
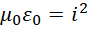
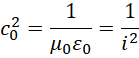
实际上是，
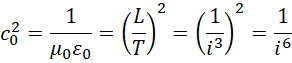
得到光速的确切表达，
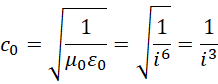
对高次幂进行折叠，
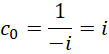
看来我们假定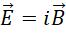
也就是，
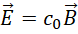
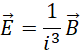
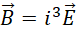
是正确的选择。回到，
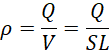
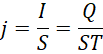
根据电荷的量子性，电荷密度的极限为电子的密度，也就是电子电量比上电子体积，电流密度的极限也是电子单位时间上走过的面积也就是电子运动方向上的截面积，也就是电子电量比上截面积和时间。所以这里的，
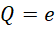
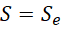
长度和时间的量子步长，就是对应的微分，
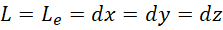
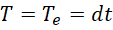
量子步长的比值，
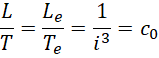
就是光速。也就是说，光速就是电子的长度和电子周期的比值，虚数单位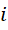 
是电子周期和电子长度的比值。从物理量角度来说，
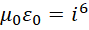
其中真空磁导率和真空介电常数都是常数，所以这个虚数单位的实际数值也是定值。我们知道电子运动起来之后会有狭义相对论效应，也就是长度和时间发生变化，但是这里的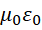 
也就是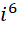 
为定值，就保证了长度和时间的比例关系不变。由此来说，只要是电子，它的光速就是不变的，或者反过来说，我们认为电子就是其长度和时间（周期）的比例为这个特殊虚数单位的数值的粒子。我们用的所有的电子系统都依赖于电子的运动或者变化，所以我们的所有电子系统的速度都不会超过这个速度。但是如果给一个电子加速，它的长度会变短，它的周期也会对应变小。那么那些更快的电子构成的长度和时间系统，相对于静止电子来说，就会具有更短的长度，以及更小的光速，因为我们会认为它们的系统的时间单位长度和我们的系统的时间单位长度是一样的。