从黎曼泽塔函数,
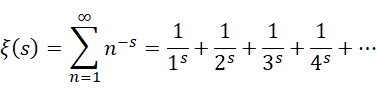
导出自然数的全加和,
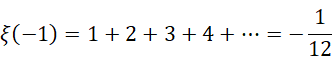
我们知道,黎曼泽塔函数的求值方程里面的数,等号左边是常规意义下的自然数或者自然数倒数幂次的全加和,等号右面是它的某种特殊对应物,而右边的数值,如果出现负数,这个负数也是复数意义上的负数,不是整数意义上的负数,也就是说,这里的 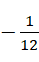 实际上是
实际上是
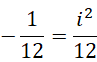
以下我们用最简单的方法解释这个数值的由来。
我们知道自然数序列的前 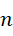 项之和为,
项之和为,
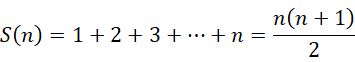
现在我们要求的是,
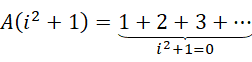
因为虚数单位具有分位的能力,对于复数形式的高维数值,我们要计算的是,首先求从1加到虚数单位 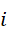 的结果,然后是求从虚数单位
的结果,然后是求从虚数单位 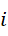 加到
加到 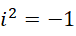 的结果,这就是两位
的结果,这就是两位 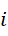 进制数的大小,也就是说,我们要的是,
进制数的大小,也就是说,我们要的是,
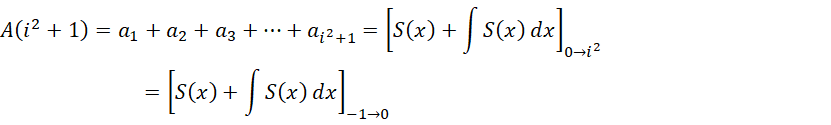
其中,
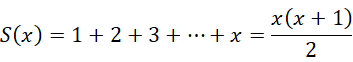
计算,
这就是 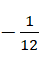 的由来。这个结果中,其它都是可想而知的,只有一点必须强调,就是,
的由来。这个结果中,其它都是可想而知的,只有一点必须强调,就是,
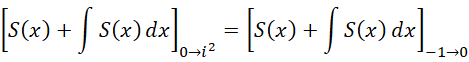
从0到 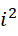 的积分,就等于从-1到0的积分,也就是说,这个结果实际上求的就是积分的补数。而这个补数是
的积分,就等于从-1到0的积分,也就是说,这个结果实际上求的就是积分的补数。而这个补数是 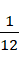 ,所以结果就是补数的相反数,也就是这个数值本身,就是
,所以结果就是补数的相反数,也就是这个数值本身,就是 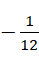 。至于为什么可以用积分算整数的全加和,这是因为相对于虚数单位以及虚数单位的平方,整数就是一阶无穷小和二阶无穷小,所以可以用积分。
。至于为什么可以用积分算整数的全加和,这是因为相对于虚数单位以及虚数单位的平方,整数就是一阶无穷小和二阶无穷小,所以可以用积分。
为了把这个事情说的更清楚一些,让我们考虑另一个序列,
同理,
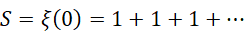
它的前 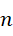 项和为,
项和为,
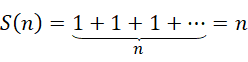
应用相同的模式,
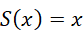
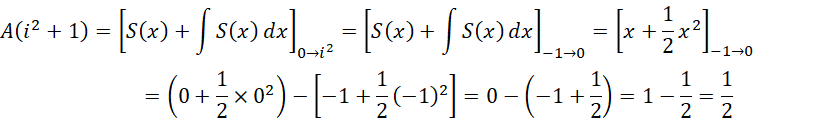
就是这个我们熟悉的结果,看来这理解目前来说是正确的。
总结来说,就是:这个"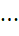 "说的是从第一项加到第
"说的是从第一项加到第 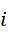 项再从第
项再从第 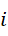 项加到第
项加到第 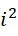 项。而第
项。而第 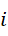 项就相当于一种无穷大,但它只是真正无穷大与一的差的平方根,也就是虚数单位;要计真正的无穷多项的和,则需要像虚数单位进制数两位那样计算这些数的累积,最后还得加上一个虚数单位项数的和。
项就相当于一种无穷大,但它只是真正无穷大与一的差的平方根,也就是虚数单位;要计真正的无穷多项的和,则需要像虚数单位进制数两位那样计算这些数的累积,最后还得加上一个虚数单位项数的和。
所以,

这就把 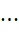 的不确定计数,变成了基于变量的确定计数,由此来说,无限项的求和问题就可以认为是变上限有限项的求和问题了。
的不确定计数,变成了基于变量的确定计数,由此来说,无限项的求和问题就可以认为是变上限有限项的求和问题了。
但是,这个S明显是,
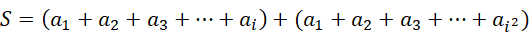
所以其实结果是除以 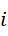 之后的结果,因为,
之后的结果,因为,
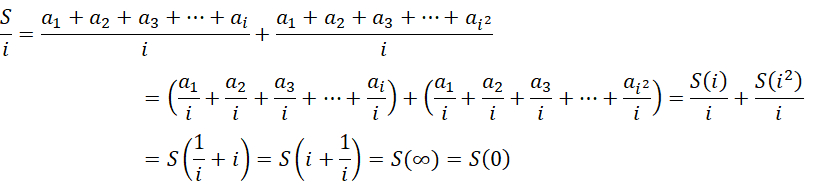
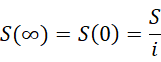
所以严格来说,
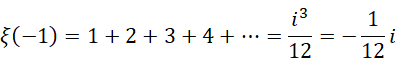
至于结果,只剩下 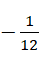 ,则意味着它是虚数单位的
,则意味着它是虚数单位的 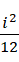 倍,或者说是单位1的
倍,或者说是单位1的 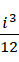 倍,结果被模掉了虚数单位。经过两次修正,我们终于得到了正确的形式。也就是说,就像我们计算质能方程的时候得到,
倍,结果被模掉了虚数单位。经过两次修正,我们终于得到了正确的形式。也就是说,就像我们计算质能方程的时候得到,
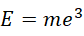
这是包含观察者在内的结果,而不包含观察者的结果则是,
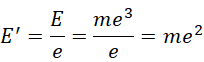
而,
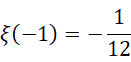
就相当于 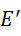 ,它是无限项之和与虚数单位的比值。这就对了,因为无限项之和等于有限的结果是非常反直觉的,但是,如果它是虚数单位的倍数,也就是说,它是某个无限项的倍数,才是它的实际值,那么这个有限的结果,就是它和无限之间的相对结果。所以还原这个结果,就是,
,它是无限项之和与虚数单位的比值。这就对了,因为无限项之和等于有限的结果是非常反直觉的,但是,如果它是虚数单位的倍数,也就是说,它是某个无限项的倍数,才是它的实际值,那么这个有限的结果,就是它和无限之间的相对结果。所以还原这个结果,就是,
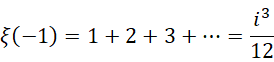
同理,
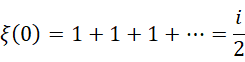
既然如此,它当然也可以等于虚数单位平方的倍数,也就是,
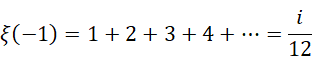
所以三个结果都是对的,
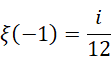
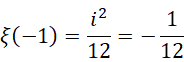
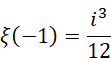
差别在于选取了不同单位。如果按照 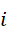 进制的向量形式来写,就是,
进制的向量形式来写,就是,
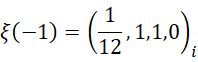
由此,这个无限项和的结果为有限项的现象就不再神秘了。
我们知道这类运算都是带有周期性的,就算是结果中带有 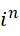 ,也一点都不奇怪,而这三个结果本质上都是纯虚数结果,只是
,也一点都不奇怪,而这三个结果本质上都是纯虚数结果,只是 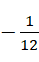 这个结果投射在了实数范围。这一点也充分证实了黎曼泽塔函数是高维结果到低维空间的投射这样一个事实。反观虚数单位,它也只是比较大的数而已,比如计算光速数值的时候推导出来的
这个结果投射在了实数范围。这一点也充分证实了黎曼泽塔函数是高维结果到低维空间的投射这样一个事实。反观虚数单位,它也只是比较大的数而已,比如计算光速数值的时候推导出来的 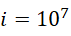 ,那么这就说明,若出现卡西米尔效应,计算卡西米尔效应的力的大小的时候,能够得到
,那么这就说明,若出现卡西米尔效应,计算卡西米尔效应的力的大小的时候,能够得到 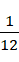 这个数值,则相关的两个单位之间,具有,
这个数值,则相关的两个单位之间,具有,
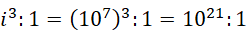
的倍数关系。换句话说,若频率出现光速数值对应的叙述单位的立方次,则有十二分之一的可能性出现卡西米尔效应。
再验证一个,
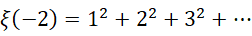
有限项和公式为,
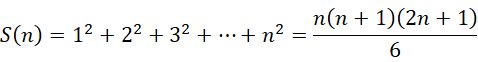
计算,
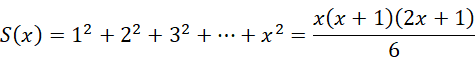
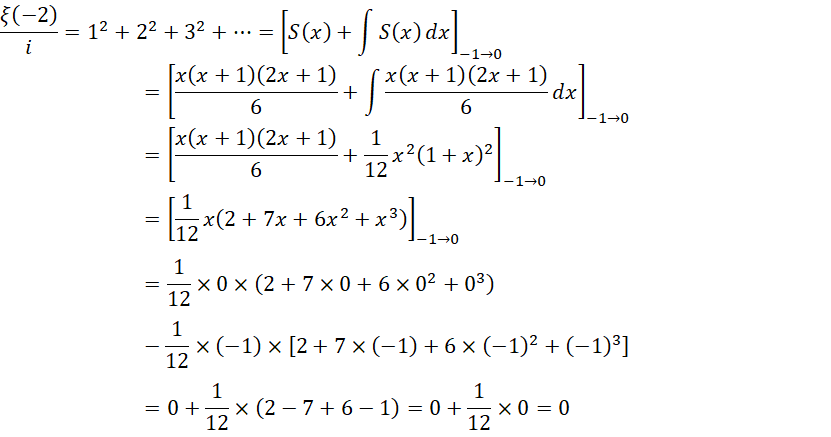
所以实际值,
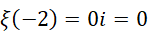
看来又对了。再看一个有争议的,
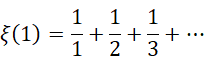
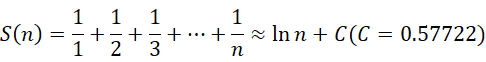
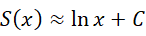
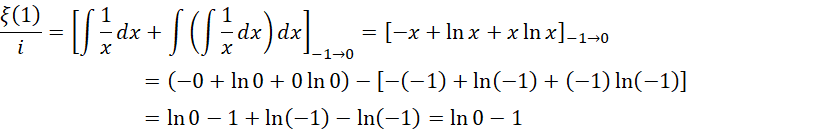
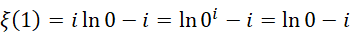
对于一阶情况,0可以被认为是虚数单位的倒数,所以它的完整形式为,
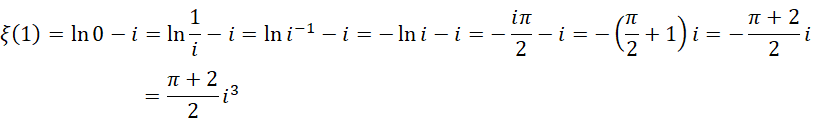
它的常规形式为,
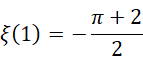
可见,虽然调和数列是发散的,但在一阶无穷小为虚数单位的倒数的前提下,仍然有确定数值。如果认为一阶无穷小为虚数单位的平方,
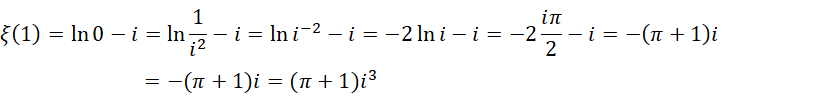
其常规形式为,
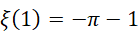
到此,再综合一下,
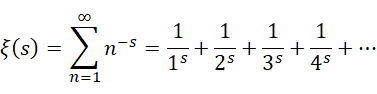
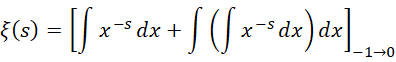
若要考虑它的数值,比如等于0,
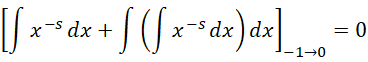
可以得出,
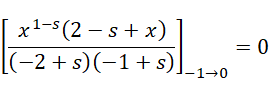
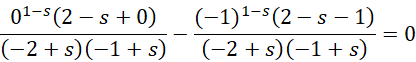
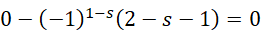
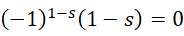
根据分母不能为0,
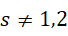
假定s可以等于1,这就对应了调和级数,这时候0的意义就是发散的或者随虚数单位的大小而定义的周期。假定s可以等于2,
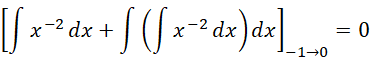
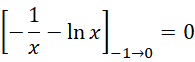
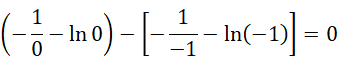
如果它严格成立,则只能是,
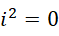
也就是,
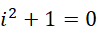
其中 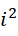 太大而忽略1的结果。目前来说这种情况不用这个算法最好。当然本来这个数值也不等于0.
太大而忽略1的结果。目前来说这种情况不用这个算法最好。当然本来这个数值也不等于0.
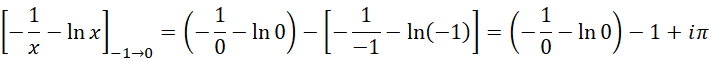
考虑二阶情况,
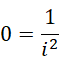
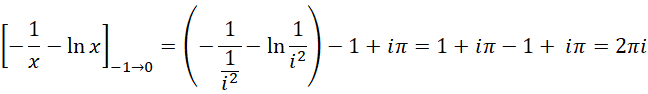
若认为 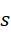 为不等于1的复数,
为不等于1的复数,
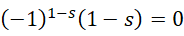
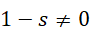
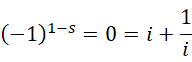
此时的0为给定虚数单位前提下的周期,方程中 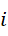 为主值,
为主值,  为微小偏移量,则方程可以写成,
为微小偏移量,则方程可以写成,
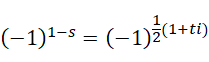
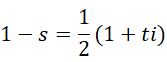
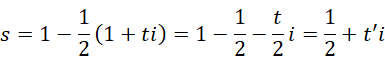
这是泽塔函数的非平凡零点。原方程还可以理解为,
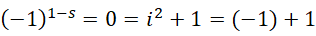
此时-1就是周期,+1是一个极小的量,忽略这个+1,
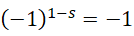
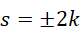
考虑到泽塔函数构成的求值方程的左右两侧的的数值大小应当相应,此时右侧是一个较大的数,左侧也必须是较大的数,所以只能取,
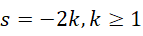
这就是泽塔函数的平凡零点。
总结一下,实际上这个做法就是显示升维解法。
我们知道对于普通自然数以及它的倒数的幂次之和,无限多个,就意味着升维。如果我们把乘以虚数单位当成一次升维,那么乘以它的平方就是二次升维,如果我们把二次升维理解为从1到无穷,那么二次升维就被认为是一次升维,而原来的一次升维就被理解为半次升维,它其实就是几何意义上的一次升维。
不难看出,
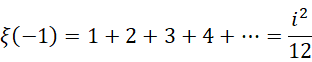
是一个几何上的二维结构,就像一个金字塔,最高一层1块砖,次高层2块砖,一直向着无限的方向延展。为了调和积分产生的三位i 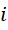 进制数结果和图像上的二维面积,我们需要对结果进行右移,而这个右移又等价于观察者的视角造成了原结果的左移。所以若是考虑观察者造成的影响,结果就是
进制数结果和图像上的二维面积,我们需要对结果进行右移,而这个右移又等价于观察者的视角造成了原结果的左移。所以若是考虑观察者造成的影响,结果就是 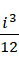 ,如果去除这个影响,结果就是
,如果去除这个影响,结果就是 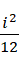 。
。