麦克斯韦方程组中电场磁场对时间的偏导数等于磁场电场的旋度这两个方程在特定的电磁过程中交替使用，就体现为电磁波的方程。我们知道电磁波是横波，也就是震动的方向垂直于其传播的方向。这里横波就对应于，
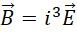
也就是磁场的每一个分量都垂直于电场的对应分量，这时我们假定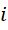 
是常量。而如果由于某些原因， 
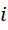成为变量，那么震动的方向就不会只是垂直于运动的方向，而在运动的方向上还会出现疏密的震荡，这时的电磁波就具有了纵波的性质。然而，我们知道这个虚数单位对于电子来说总是定值，不管是否对其加速，都是定值，或者说，我们选择了具有这样的时空比例的震动来充当电子。所以说从电子的外部改变这个虚数单位的数值，进而产生纵波是不可能的。但是，通过调节磁场和电场的比例，进而创造或者选择特定的电磁比例模式，是完全可能的。用这种模式创造或者选择这样的电子，也是完全可能的。而此时，光速就是可变的了。
回到，
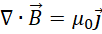
这个方程不是麦克斯韦方程组原始的方程，而是根据电磁对称性写出的方程。这个方程意味着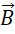 
具有非零的散度，也就是说，磁场是有源有宿的，但是我们知道，在空间中，磁场是无源无宿的。若它有源有宿，就只能不在三维空间中。但若考虑到，
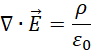
以及，
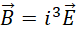
则可以认为，
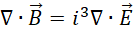
也就是，
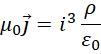
由此可以知道的是，
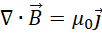
的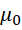 
中是含有虚数单位 
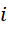的。有旋无源的 
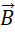，无源的原因，是因为它的方向正交于 
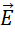。我们知道 
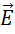在三维空间中，而 
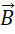与其正交，那么 
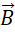的散度方向，就只能在第四维上。回到，
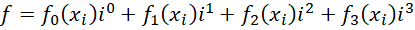
它已经有四个维数，第一个维数是0维，现在将其扩展到第四维（一共五维），
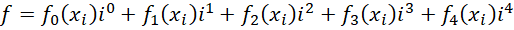
由于，
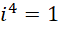
合并同类项，得到五维表达式，
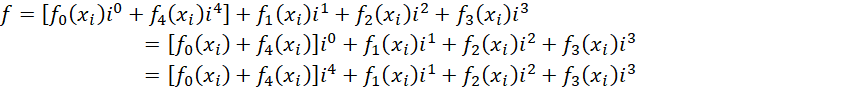
可见，若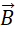 
的散度不为0，则必定导致单位1的变化，或者说，方程组可以产生纵波。而这个产生纵波的能力，也就是定义单位1的能力。
对于，
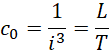
来说，虽然不会改变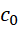 
的大小，但是 
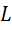和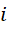 
不变的前提下，它可以决定 
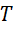的大小，也就是时间流逝的快慢。这个场景指的是，相对于观察者静止的惯性系，却有不同于观察者时间流逝的速度，这是因为决定时间的磁场与通常意义下的磁场不同。
考虑质能方程，
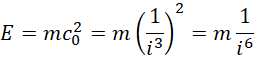
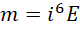
对比电磁关系，
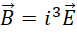
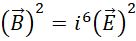
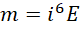
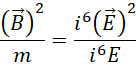
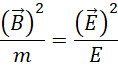
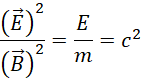
观察这一步，
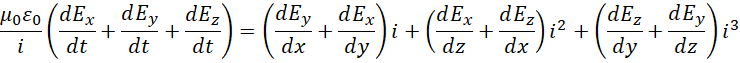
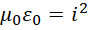
以及后来得到的，
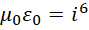
将其泛化，
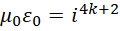
代入，
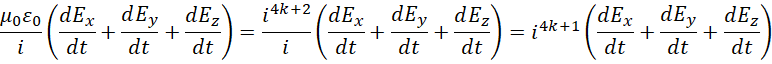
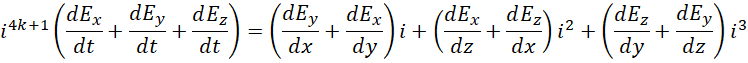
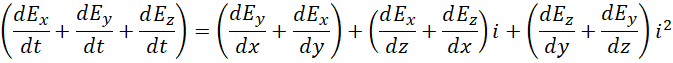
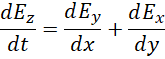
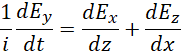
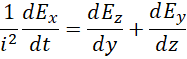
根据以上提示，假定，
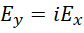
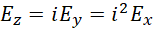
重写三个关系，
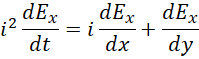
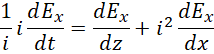
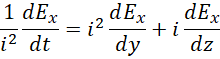
约去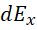 
，
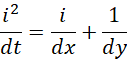
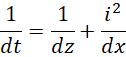
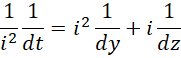
左边对齐，
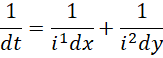
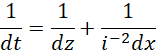
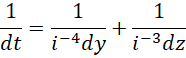
两边取倒数，
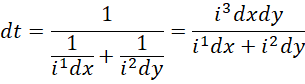
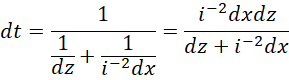
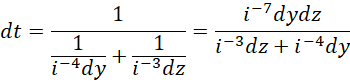
得到，
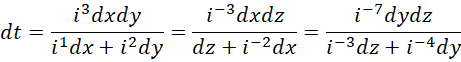
假设，
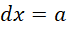
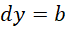
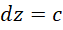
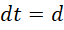
我们把虚数单位的高次幂和负数幂约化到常规的形式，
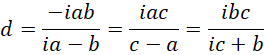
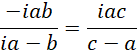
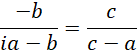
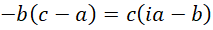
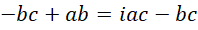
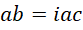
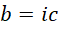
试着解，
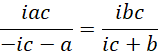
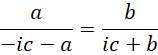
代入，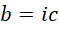
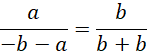
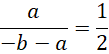
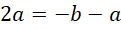
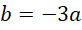
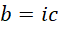
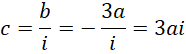
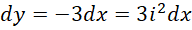
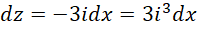
我们知道，方程的左边是，
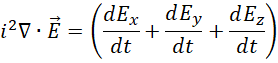
右边是，
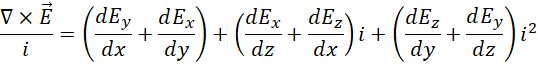
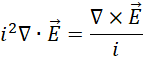
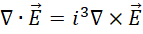
这里不只是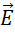 
而是任何向量，所以
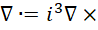
或者，
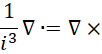
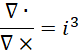
也就是说，一个向量场的散度和它的旋度的所有分量的比值都是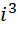 
。
用电磁学的图像来描述，可以认为那个环绕电流的磁场（物质），之所以出现环绕的效果，其必要条件，是它的频率或者周期，是构成电流的电子的频率或者周期的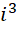 
倍。在常规形式（虚数单位幂次被正规化到0到3区间）下，只要满足这个条件，无论空间长度在三个维数上的最小单位取任何数值，都可以获得有效的最小单位时间。