第二届电力电子技术与电网系统国际学术会议（PETGS 2026）

重要信息

官网： https://ais.cn/u/ERRza2

**时间：**2026年1月9-11日

**地点：**安徽·蚌埠

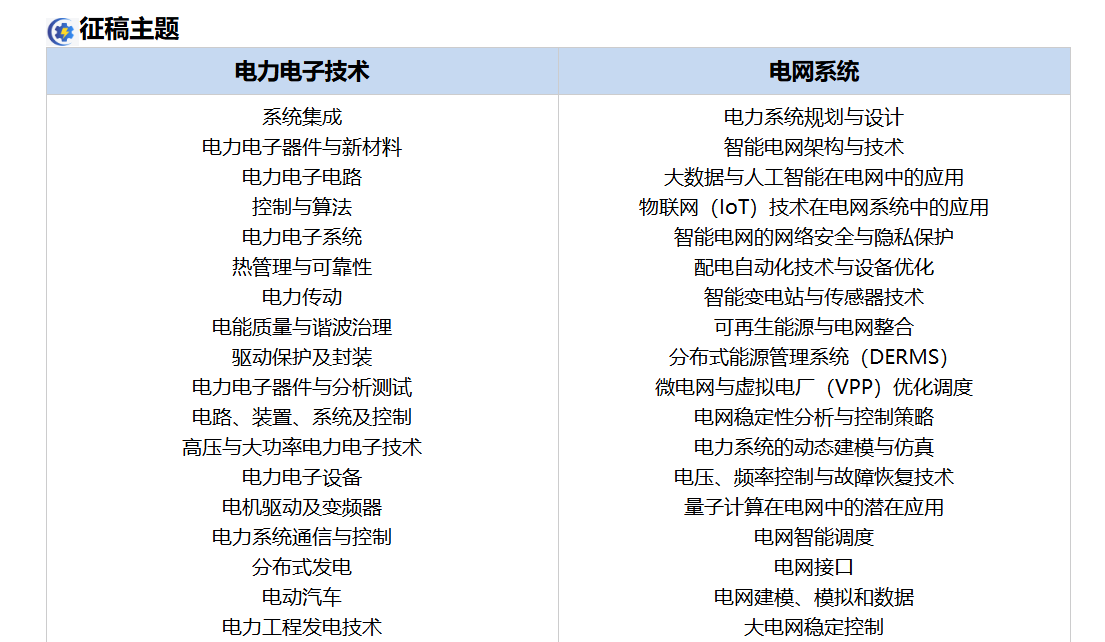
征稿主题

一、电力电子技术与电网系统的融合背景

电力电子技术是实现电能变换、控制与优化的核心技术，涵盖整流、逆变、斩波等核心拓扑；电网系统则是电能生产、传输、分配的基础设施，正朝着智能化、柔性化、低碳化方向转型。第二届电力电子技术与电网系统国际学术会议（PETGS 2026）聚焦该领域前沿技术与工程应用，本文从技术原理、算法实现、工程落地维度，解析电力电子装置控制、电网谐波治理、新能源并网等核心知识点，结合 Python 代码实现关键技术场景落地。

二、核心技术方向及知识点解析

2.1 电力电子装置的建模与控制（以三相 PWM 整流器为例）

三相 PWM 整流器是新能源并网、电网无功补偿的核心电力电子装置，其精准建模与控制是保障电网电能质量的关键。

2.1.1 三相 PWM 整流器核心参数与控制维度

控制维度	核心参数	控制目标	常用算法
直流侧电压控制	直流母线电压、电压纹波	稳定直流侧电压，纹波最小化	PI 控制、滑模控制
交流侧电流控制	并网电流、功率因数	单位功率因数并网，谐波最小	电流内环 PI、PR 控制
网侧谐波抑制	谐波含量（THD）、畸变率	降低并网电流 THD 至国标以内	重复控制、有源滤波
故障容错控制	开关管故障、电压暂降	保障装置持续稳定运行	模型预测控制、容错拓扑

2.1.2 Python 实现三相 PWM 整流器仿真与控制

以下代码实现三相 PWM 整流器的数学建模与 PI 控制仿真，涵盖交流侧电流、直流侧电压的闭环控制：

python

运行

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# 1. 三相PWM整流器参数定义
class PWMRectifier:
    def __init__(self):
        # 电网参数
        self.Vs = 220  # 电网相电压有效值(V)
        self.fs = 50   # 电网频率(Hz)
        self.w = 2 * np.pi * self.fs  # 角频率(rad/s)
        # 整流器参数
        self.L = 0.005  # 网侧电感(H)
        self.R = 0.1    # 电感等效电阻(Ω)
        self.C = 2000e-6 # 直流侧电容(F)
        self.RL = 100   # 直流侧负载电阻(Ω)
        # 控制参数
        self.kp_v = 0.8  # 电压环PI比例系数
        self.ki_v = 20   # 电压环PI积分系数
        self.kp_i = 0.2  # 电流环PI比例系数
        self.ki_i = 100  # 电流环PI积分系数
        # 状态变量
        self.vdc = 600   # 初始直流侧电压(V)
        self.id = 0      # d轴电流(A)
        self.iq = 0      # q轴电流(A)
        self.err_v_int = 0  # 电压环积分误差
        self.err_id_int = 0 # d轴电流积分误差
        self.err_iq_int = 0 # q轴电流积分误差

    # 三相abc转dq0坐标变换
    def abc2dq(self, ia, ib, ic, theta):
        T = 2/3 * np.array([
            [np.cos(theta), np.cos(theta-2*np.pi/3), np.cos(theta+2*np.pi/3)],
            [-np.sin(theta), -np.sin(theta-2*np.pi/3), -np.sin(theta+2*np.pi/3)],
            [0.5, 0.5, 0.5]
        ])
        iabc = np.array([ia, ib, ic]).reshape(3,1)
        idq0 = T @ iabc
        return idq0[0,0], idq0[1,0]

    # dq0转abc坐标变换
    def dq2abc(self, id, iq, theta):
        T = np.array([
            [np.cos(theta), -np.sin(theta), 1],
            [np.cos(theta-2*np.pi/3), -np.sin(theta-2*np.pi/3), 1],
            [np.cos(theta+2*np.pi/3), -np.sin(theta+2*np.pi/3), 1]
        ])
        idq0 = np.array([id, iq, 0]).reshape(3,1)
        iabc = T @ idq0
        return iabc[0,0], iabc[1,0], iabc[2,0]

    # PI控制器
    def pi_controller(self, ref, feedback, kp, ki, err_int):
        err = ref - feedback
        err_int += err * 1e-5  # 积分项（步长1e-5s）
        output = kp * err + ki * err_int
        return output, err_int

    # 整流器状态更新
    def update(self, t):
        # 电网电压瞬时值
        theta = self.w * t
        va = self.Vs * np.sqrt(2) * np.cos(theta)
        vb = self.Vs * np.sqrt(2) * np.cos(theta - 2*np.pi/3)
        vc = self.Vs * np.sqrt(2) * np.cos(theta + 2*np.pi/3)

        # 电压环控制（直流电压参考值600V）
        vdc_ref = 600
        id_ref, self.err_v_int = self.pi_controller(vdc_ref, self.vdc, 
                                                    self.kp_v, self.ki_v, self.err_v_int)
        # q轴电流参考值为0（单位功率因数）
        iq_ref = 0

        # 电流环控制
        vd_ref, self.err_id_int = self.pi_controller(id_ref, self.id, 
                                                      self.kp_i, self.ki_i, self.err_id_int)
        vq_ref, self.err_iq_int = self.pi_controller(iq_ref, self.iq, 
                                                      self.kp_i, self.ki_i, self.err_iq_int)

        # 电流状态方程
        did_dt = (1/self.L) * (va - self.R * self.id + self.w * self.L * self.iq - vd_ref)
        diq_dt = (1/self.L) * (vb - self.R * self.iq - self.w * self.L * self.id - vq_ref)
        
        # 直流侧电压状态方程
        id_abc, iq_abc, _ = self.dq2abc(self.id, self.iq, theta)
        p_ac = 1.5 * (self.Vs * self.id)  # 交流侧输入功率
        p_dc = self.vdc**2 / self.RL      # 直流侧输出功率
        dvdc_dt = (p_ac - p_dc) / (self.C * self.vdc)

        # 更新状态
        self.id += did_dt * 1e-5
        self.iq += diq_dt * 1e-5
        self.vdc += dvdc_dt * 1e-5

        return self.vdc, self.id, self.iq

# 2. 仿真运行
rectifier = PWMRectifier()
t_sim = np.arange(0, 0.5, 1e-5)  # 仿真时间0.5s，步长1e-5s
vdc_list = []
id_list = []
iq_list = []

for t in t_sim:
    vdc, id, iq = rectifier.update(t)
    vdc_list.append(vdc)
    id_list.append(id)
    iq_list.append(iq)

# 3. 仿真结果分析
print("三相PWM整流器仿真结果：")
print(f"直流侧电压稳态值：{np.mean(vdc_list[-1000:]):.2f} V（参考值600V）")
print(f"d轴电流稳态值：{np.mean(id_list[-1000:]):.2f} A")
print(f"q轴电流稳态值：{np.mean(iq_list[-1000:]):.2f} A（参考值0A）")

# 计算直流电压纹波
vdc_ripple = np.max(vdc_list[-1000:]) - np.min(vdc_list[-1000:])
print(f"直流侧电压纹波：{vdc_ripple:.2f} V")

2.2 电网系统的谐波检测与治理

电网谐波是电力电子装置并网带来的核心电能质量问题，精准的谐波检测是治理的前提，常用方法包括快速傅里叶变换（FFT）、小波变换等。

2.2.1 Python 实现电网谐波检测与 THD 计算

以下代码实现基于 FFT 的电网电流谐波检测，计算总谐波畸变率（THD），为有源电力滤波器（APF）治理提供依据：

python

运行

import numpy as np
from scipy.fftpack import fft, fftfreq
from scipy.signal import butter, filtfilt

# 1. 构建含谐波的电网电流数据
np.random.seed(42)
fs = 10000  # 采样频率(Hz)
t = np.linspace(0, 1, fs, endpoint=False)
f0 = 50     # 基波频率(Hz)

# 基波+3/5/7次谐波+噪声
i_grid = (10 * np.sin(2 * np.pi * f0 * t) +          # 基波（50Hz）
          2 * np.sin(2 * np.pi * 3*f0 * t) +         # 3次谐波（150Hz）
          1.5 * np.sin(2 * np.pi * 5*f0 * t) +       # 5次谐波（250Hz）
          1 * np.sin(2 * np.pi * 7*f0 * t) +         # 7次谐波（350Hz）
          0.5 * np.random.normal(0, 1, len(t)))      # 测量噪声

# 2. 谐波检测（FFT）
def harmonic_detection(signal, fs, f0):
    # FFT计算
    N = len(signal)
    yf = fft(signal)
    xf = fftfreq(N, 1/fs)[:N//2]
    yf_amp = 2.0/N * np.abs(yf[:N//2])  # 幅值谱

    # 提取各次谐波幅值
    harmonics = {}
    for n in [1,3,5,7,9]:  # 1(基波)、3、5、7、9次谐波
        freq = n * f0
        # 找到最接近的频率点
        idx = np.argmin(np.abs(xf - freq))
        harmonics[f'n{n}'] = yf_amp[idx]
    
    # 计算THD（总谐波畸变率）
    fundamental = harmonics['n1']
    harmonic_sum = sum([v**2 for k,v in harmonics.items() if k!='n1'])
    thd = np.sqrt(harmonic_sum) / fundamental * 100

    return harmonics, thd, xf, yf_amp

# 3. 执行谐波检测
harmonics, thd, xf, yf_amp = harmonic_detection(i_grid, fs, f0)

# 4. 结果输出
print("\n电网电流谐波检测结果：")
for n, amp in harmonics.items():
    print(f"{n}次谐波幅值：{amp:.2f} A")
print(f"总谐波畸变率（THD）：{thd:.2f} %")

# 5. 谐波治理（模拟APF补偿）
# 设计陷波滤波器去除3/5/7次谐波
def butter_notch_filter(data, fs, freq_list):
    filtered_data = data.copy()
    for freq in freq_list:
        nyq = 0.5 * fs
        freq = freq / nyq
        # 陷波滤波器设计
        b, a = butter(4, [freq-0.01, freq+0.01], btype='bandstop')
        filtered_data = filtfilt(b, a, filtered_data)
    return filtered_data

# 补偿3/5/7次谐波
compensated_current = butter_notch_filter(i_grid, fs, [150, 250, 350])
# 计算补偿后THD
_, thd_compensated, _, _ = harmonic_detection(compensated_current, fs, f0)
print(f"谐波补偿后THD：{thd_compensated:.2f} %")

2.3 新能源并网的电网稳定性分析

风电、光伏等新能源并网易引发电网电压波动、频率偏移等稳定性问题，基于暂态稳定分析的控制策略是保障电网安全的核心。

2.3.1 Python 实现新能源并网暂态稳定分析

以下代码实现基于改进欧拉法的新能源并网电网暂态稳定仿真，分析故障下电网频率、电压的暂态响应：

python

运行

import numpy as np
import pandas as pd

# 1. 电网暂态稳定模型
class GridStability:
    def __init__(self):
        # 电网参数
        self.f_nom = 50  # 额定频率(Hz)
        self.V_nom = 380 # 额定线电压(V)
        self.H = 5       # 系统惯性时间常数(s)
        self.D = 2       # 阻尼系数
        # 新能源参数（风电+光伏）
        self.P_wind = 20 # 风电出力(MW)
        self.P_pv = 15   # 光伏出力(MW)
        self.P_load = 30 # 负荷功率(MW)
        # 暂态参数
        self.f = 50      # 初始频率(Hz)
        self.df_dt = 0   # 频率变化率
        self.V = 380     # 初始电压(V)

    # 暂态稳定状态方程
    def transient_model(self, t, fault_type=None):
        # 功率不平衡计算
        P_gen = self.P_wind + self.P_pv
        if fault_type == '三相短路' and (t > 0.1 and t < 0.2):
            # 0.1-0.2s发生三相短路故障，新能源出力骤降
            P_gen *= 0.2
        
        P_imbalance = P_gen - self.P_load

        # 频率动态方程
        df_dt = (P_imbalance) / (2 * self.H) - (self.D / (2 * self.H)) * (self.f - self.f_nom)
        self.df_dt = df_dt
        self.f += df_dt * 1e-3

        # 电压动态方程（简化模型）
        dv_dt = -0.1 * (self.V - self.V_nom) - 0.05 * P_imbalance
        self.V += dv_dt * 1e-3

        return self.f, self.V

# 2. 暂态仿真
stability = GridStability()
t_sim = np.arange(0, 2.0, 1e-3)  # 2s仿真时长，步长1ms
freq_list = []
volt_list = []
fault_flag = []

for t in t_sim:
    # 0.1-0.2s模拟三相短路故障
    fault = '三相短路' if (t > 0.1 and t < 0.2) else None
    f, v = stability.transient_model(t, fault)
    freq_list.append(f)
    volt_list.append(v)
    fault_flag.append(1 if fault else 0)

# 3. 稳定性分析
df_result = pd.DataFrame({
    'time(s)': t_sim,
    'frequency(Hz)': freq_list,
    'voltage(V)': volt_list,
    'fault': fault_flag
})

# 关键指标计算
freq_drop = np.min(freq_list) - stability.f_nom
volt_drop = np.min(volt_list) - stability.V_nom
recovery_time_freq = np.where(np.abs(np.array(freq_list) - 50) < 0.1)[0][-1] * 1e-3
recovery_time_volt = np.where(np.abs(np.array(volt_list) - 380) < 5)[0][-1] * 1e-3

print("\n新能源并网暂态稳定分析结果：")
print(f"故障期间最大频率跌落：{freq_drop:.2f} Hz（国标允许±0.5Hz）")
print(f"故障期间最大电压跌落：{volt_drop:.2f} V")
print(f"频率恢复至额定值±0.1Hz时间：{recovery_time_freq:.2f} s")
print(f"电压恢复至额定值±5V时间：{recovery_time_volt:.2f} s")

# 稳定性判定
if np.min(freq_list) > 49.5 and np.min(volt_list) > 360:
    print("电网暂态稳定：满足新能源并网稳定要求")
else:
    print("电网暂态失稳：需优化新能源并网控制策略")

三、技术挑战与发展趋势

3.1 现存技术挑战

1. 宽频带谐波治理：电力电子装置多频段谐波叠加，传统滤波方法难以实现全频段精准治理；
2. 新能源并网稳定性：高比例新能源并网导致电网惯性降低，频率 / 电压调节能力不足；
3. 电力电子装置可靠性：高温、高电压工况下，功率器件寿命衰减快，故障预警难度大；
4. 电网柔性控制：多端柔直电网的协调控制，面临时延、信息不对称等问题；
5. 数字化转型瓶颈：电网海量数据采集与实时分析，受限于边缘算力与通信带宽。

3.2 未来发展趋势

1. 碳化硅（SiC）/ 氮化镓（GaN）器件应用：宽禁带半导体器件提升电力电子装置效率、降低体积，适配新能源并网需求；
2. 虚拟同步机技术（VSG）：为新能源电站赋予虚拟惯性，提升电网频率 / 电压支撑能力；
3. 数字孪生电网：构建电力电子装置 - 电网系统数字孪生体，实现全生命周期仿真与优化；
4. AI 驱动的自适应控制：基于强化学习的电力电子装置控制策略，自适应电网工况变化；
5. 光储充一体化管控：融合电力电子变换、储能调度、充电桩控制，提升分布式能源利用率；
6. 电网韧性提升技术：基于电力电子装置的电网故障快速隔离与自愈控制，降低停电损失。

四、总结

电力电子技术与电网系统的深度融合，是实现电网智能化、低碳化转型的核心路径。从电力电子装置的精准控制，到电网谐波的高效治理，再到新能源并网的稳定保障，技术创新正在重构电网运行的底层逻辑。PETGS 2026 会议聚焦该领域的前沿研究与工程实践，为全球电力电子与电网领域的研究者、工程师搭建了交流平台。未来需突破器件、控制、系统协同等核心瓶颈，推动电力电子技术更好地服务于新型电力系统建设，实现电网安全、高效、低碳运行。

五、国际交流与合作机会

作为国际学术会议，将吸引全球范围内的专家学者参与。无论是发表研究成果、聆听特邀报告，还是在圆桌论坛中与行业大咖交流，都能拓宽国际视野，甚至找到潜在的合作伙伴。对于高校师生来说，这也是展示研究、积累学术人脉的好机会。