动态规划（一）算法设计与分析 国科大

这篇文章并不是老师讲述的内容，主要是我DP学的太差了，所以补一篇来强化基础

首先先介绍一下动态规划：

和分治一样，动态规划也是将大问题拆分成小问题，不同的是，动态规划专门对付那些 "小问题会重复出现" 的情况，核心是 "把小问题的答案记下来，不用反复算，再用小问题的答案拼出大问题的答案"。而分治的子问题通常是独立不重复的。

下面看一个动态规划的例子

爬楼梯

假设你要爬 10 级楼梯，每次只能爬 1 级或 2 级，问有多少种不同的爬法？

• 如果你用 "暴力试"：想知道爬 10 级的方法，得先算爬 9 级和爬 8 级的方法（因为最后一步要么从 9 级爬 1 级，要么从 8 级爬 2 级）；而算爬 9 级的方法，又得先算爬 8 级和 7 级的方法...... 这里 "爬 8 级的方法" 会被算两次（算 10 级时要算 8 级，算 9 级时也要算 8 级），反复计算会浪费很多时间。

• 而用动态规划：

  1. 先算 "小问题" 的答案：
     • 爬 1 级：只有 1 种方法（直接爬 1 级），记下来：dp[1]=1；
     • 爬 2 级：有 2 种方法（1+1，或直接爬 2 级），记下来：dp[2]=2；
  2. 用小问题的答案拼大问题：
     • 爬 3 级 = 爬 2 级的方法 + 爬 1 级的方法 → dp[3]=dp[2]+dp[1]=3；
     • 爬 4 级 = 爬 3 级的方法 + 爬 2 级的方法 → dp[4]=dp[3]+dp[2]=5；
     • ...... 以此类推，直到算出dp[10]。

可以看到，我们通过利用之前求解过的子问题，极大减少了计算步骤。（这个例子和求解斐波那契数列几乎一致）

再看一个例子：

凑零钱

要凑出 10 块钱，只有 1 块、2 块、5 块的硬币，问最少需要几个硬币？

• 动态规划的思路是：
  1. 先算 "凑出小金额" 的最少硬币数：
     • 凑 1 块：最少 1 个（1 块），记dp[1]=1；
     • 凑 2 块：最少 1 个（2 块），记dp[2]=1；
     • 凑 3 块：要么 "凑 2 块 + 1 块"（1+1=2 个），要么 "凑 1 块 + 2 块"（1+1=2 个），记dp[3]=2；
  2. 凑 10 块的最少硬币数 = 以下三种情况的最小值：
     • 凑 9 块的最少硬币数 + 1 个 1 块 → dp[9]+1；
     • 凑 8 块的最少硬币数 + 1 个 2 块 → dp[8]+1；
     • 凑 5 块的最少硬币数 + 1 个 5 块 → dp[5]+1。

同样的，也是利用已知的小问题来拼接成我们要求的大问题

总结一下动态规划的特点：

1. 能拆：大问题可以拆成多个小问题；
2. 重复：小问题会被反复用到，所以记下来省时间；
3. 能拼：大问题的答案，能从 "小问题的答案" 里组合出来。

一般来说，我们会用一个数据结构来记录重复的子问题。（本文中涉及的问题都比较基础，因此都用数组dpn来进行记录，求解动态规划问题的核心，也就是求解dpn）

下面看一个爬楼梯的进阶版

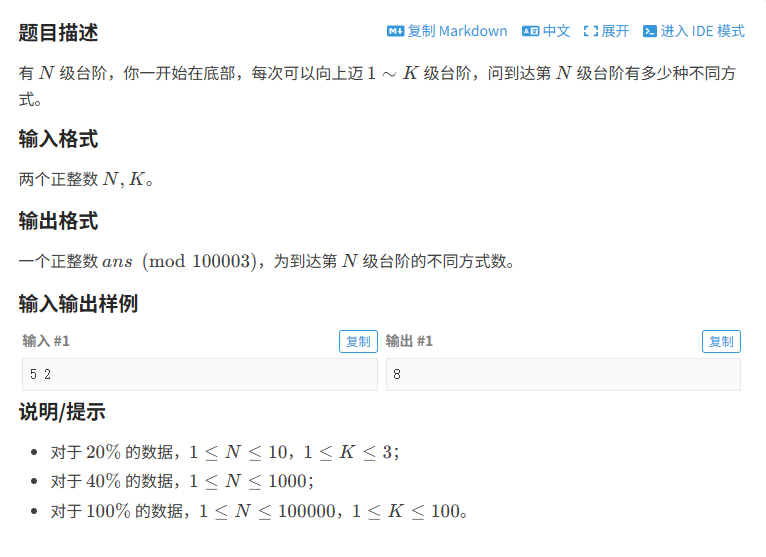
现在一次最多可以爬上的台阶从2变为了k，但是逻辑是一样的。

当处于第i个台阶时，共有k种情况可以爬到：

从第i-k阶直接爬k个台阶；

从第i-k+1阶直接爬k+1个台阶

从第i-k+2阶直接爬k-2个台阶

..............

总结一下，要到达第 i 级台阶，最后一步的步数只能是 1~K 中的某一个（假设最后一步迈了 j 级，j∈1,K），因此：到达第 i 级的方式数 = 所有 "到达第 i-j 级的方式数" 之和（j 从 1 到 K，但需满足 i-j ≥ 0，否则 i-j 不存在）

因此，我们可以尝试写出一种计算dpn（假设K=3）：

dp1，即爬上第1个台阶有几种方式，显然只有1种方式，从最底（dp0）一次爬1个台阶，因此dp1=dp0=1；

dp2，即爬上第2个台阶有几种方式，可以从最底（dp0）一次爬两个台阶，也可以从第1个台阶（dp1）再爬一个台阶，因此dp2=dp1+dp0=2；

dp3，即爬上第3个台阶有几种方式，可以从最底（dp0）一次爬3个台阶，也可以从第1个台阶（dp1）再爬两个台阶，还可以从第2个台阶（dp2）爬一个台阶，因此dp3=dp2+dp1+dp0=4；

dp4，即爬上第4个台阶有几种方式，可以从第1个台阶（dp1）一次爬3个台阶，也可以从第2个台阶（dp2）再爬两个台阶，还可以从第3个台阶（dp3）爬一个台阶，因此dp4=dp3+dp2+dp1=7；

dp5，即爬上第5个台阶有几种方式，可以从第2个台阶（dp2）一次爬3个台阶，也可以从第3个台阶（dp3）再爬两个台阶，还可以从第4个台阶（dp4）爬一个台阶，因此dp5=dp4+dp3+dp2=13；

............

dpn，即爬上第n个台阶有几种方式，可以从第n-3个台阶（dpn-3）一次爬3个台阶，也可以从第n-2个台阶（dpn-2）再爬两个台阶，还可以从第n-1个台阶（dpn-1）爬一个台阶，因此dpn=dpn-3+dpn-2+dpn-1；

---

上例中K=3，那么能直接写出K=4时候的dpn吗？大家可以尝试一下：

dpn=dpn-4+dpn-3+dpn-2+dpn-1；

同样的，K=5、K=6也很容易写出，我们把这样的等式称为状态转移方程。

到达第 i 级的方式数 = 所有 "到达第 i-j 级的方式数" 之和（j 从 1 到 K，但需满足 i-j ≥ 0，否则 i-j 不存在）

由此可以通过双循环，外部循环控制数组dp的值，内部循环j 从 1 到 K来计算。

代码如下：

#include<bits/stdc++.h>
using namespace std;

int n, k, dp[1000000];
int ans = 100003;

int main()
{
    cin >> n >> k;
    dp[0] = 1;
    dp[1] = 1;
    for(int i = 2; i <= n; i++)
    {
        for(int j = 1; j <= k; j++)
        {
            if(i >= j)
            dp[i] = (dp[i] + dp[i - j]) % ans;
        }
    }
    cout << dp[n] % ans;
}

下一篇文章仍会有两个较为简单的例子来理解DP。