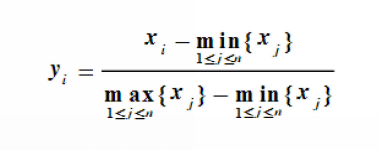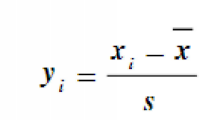介绍线性回归
线性回归是利用数理统计中回归分析，来确定两种或两种以上变量 间相互依赖的定量关系的一种统计分析方法
相关关系：包含因果关系和平行关系
因果关系：回归分析（原因引起结果，需要明确自变量和因变量）
平行关系：相关分析（无因果关系，不区分自变量和因变量）
一元线性回归模型
一元线性回归模型是分析一个自变量（X） 与一个因变量（Y） 之间线性关系的统计模型，核心表达式为：Y = β₀ + β₁X + ε
其中：
• β₀ 是截距项（X=0时Y的估计值），β₁ 是斜率（X每变化1单位，Y的平均变化量）；
• ε 是随机误差项（表示模型无法解释的Y的变异，满足均值为0、方差恒定等假设）。
误差项：除线性因素外的随机因素所产生的误差
多元线性回归模型
多元线性回归模型是分析多个自变量（X₁, X₂, ..., Xₖ） 与一个因变量（Y） 之间线性关系的统计模型，核心表达式为：Y = β₀ + β₁X₁ + β₂X₂ + ... + βₖXₖ + ε
其中：
β₀ 是截距项（所有自变量为0时Y的估计值），β₁~βₖ 是偏回归系数（某一自变量变化1单位、其他自变量固定时，Y的平均变化量）；
ε 是随机误差项（满足均值为0、方差恒定、独立性、正态性等假设）。
误差项分析
1.误差项可以省略吗？
答：误差项不可省略，误差是必然产生的。并且由于产生了误差项，我们便可以基于误差的特点来进行对线性回归的参数估计的。
2.误差项有什么特点？
答：独立同分布。
独立：每个样本点都是独立的；
例：贷款，每个人与每个人之间是没有联系的，贷多少钱完全基于你的工资。
同分布：同分布就是我的这套估计体系是我人民银行的估计体系，每个人都是服从我的分布体系，不会使用别人的，也就是说每个样本点都处于同一个分布函数下。
3.误差项满足高斯分布
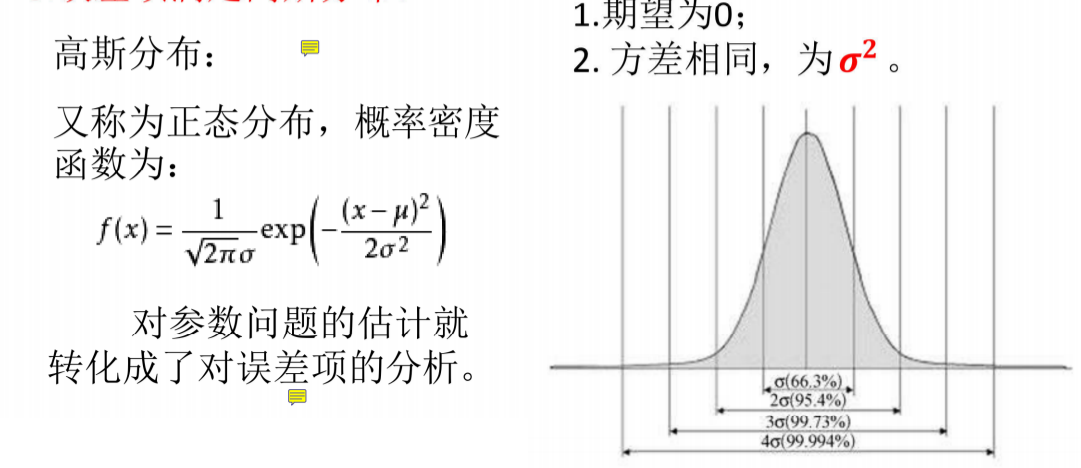
极大似然估计
极大似然估计是一种统计方法，用于估计概率模型的参数。其核心思想是选择能够使观测数据出现概率最大的参数值。通过最大化似然函数或对数似然函数，找到最符合数据的参数估计。
似然函数求解
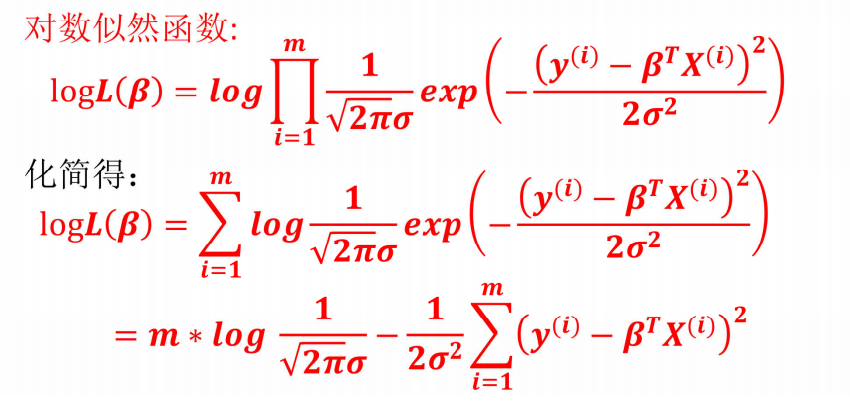
解答：
1、对数函数y=ln x是严格单调递增函数，原似然函数L(β)的最大值点与对数似然函数log L(β)的最大值点完全相同。
对数变换能将似然函数的乘积运算转化为加法运算，大幅简化极大似然估计的计算过程，不改变极值点的位置。
2、保留1/2是为了简化求导预算
3、对数似然函数中的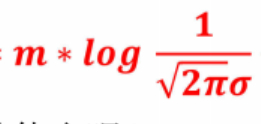
是与参数β无关的常数项，在对\beta求极值时，常数项的导数为0，不影响极值点的求解，因此可从目标函数中删除。
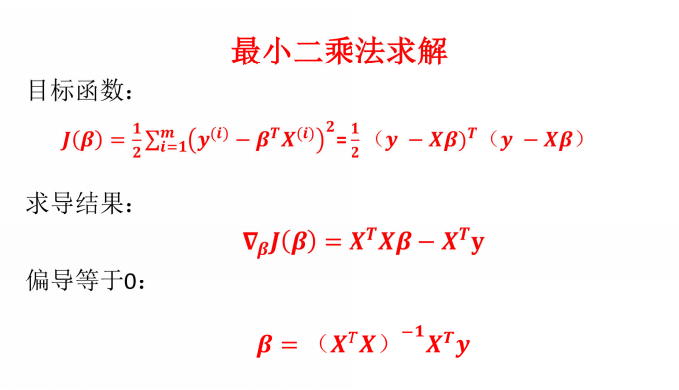
相关系数
又称皮尔逊相关系数，是研究变量之间相关关系的度量，一般用字母r表示
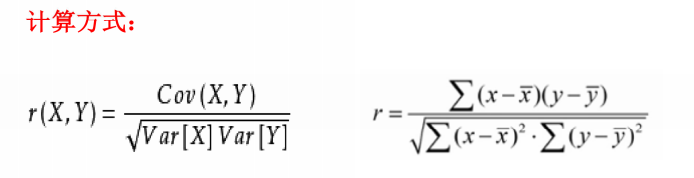
Cov（X,Y）为X与Y的协方差
Var[X]为X的方差
Var[Y]为Y的方差
相关系数的解释：
-
|r|≥0.8时，视为两个变量之间高度相关
-
0.5≤|r|<0.8时，视为中度相关
-
0.3≤|r|<0.5时，视为低度相关
-
|r|<0.3时，说明两个变量之间的相关程度极弱，可视为不相关
拟合优度
其中，分子第一个y表示预测值，第二个y表示平均值，分母第一个y表示真实值
statsmodels
statsmodels是一个有很多统计模型的python库，能完成很多统计测试，数据探索以及可视化。它也包含一些经典的统计方法，比如贝叶斯方法等。
• 线性模型
• 线性混合效应模型
• 方差分析方法
• 时间序列模型
• 广义矩阵估计方法
三种检验方法
前面计算的前提是：数据集中的数据都是独立同分布的。并且误差都是满足正太分布的。
但是这个前提是否能100%确定呢。所以提出如下的检验方法：
假设检验
原理：小概率原理：小概率事件在一次抽样中不会发生。
H0：原假设 【希望原假设被接受】
H1：备择假设 【与原假设对立】
接受H0与拒绝H0的判别方法：看小概率事件是否发生。
假设检验的步骤
- 先假设H0是真的，然后判别小概率事件是否发生，如果发生，就拒绝H0，接受H1，如果没有发生，就接受H0。
解释：整体的思想为小概率事件在一次抽样中不发生，小概率事件不发生是极大概率事件，所以上面的假设就是合理的。
- 深入思考，如果小概率事件发生了，此时却拒绝了H0，就是拒绝了真实的情况，那么就犯了第一类错误，即拒真；拒真的概率就是我们所定的\alpha，即显著性水平，一般\alpha=0.05。
第一类错误：P(\text{拒绝}H0|H0\text{真})=\alpha
第二类错误：P(\text{接受}H0|H0\text{假})=\beta
F检验（线性关系）
目的：检验自变量x与因变量y之间的线性关系是否显著，或者说，他们之间能否用一个线性模型来表示。【对于整个方程显著性的检验】
T检验（回归系数）
目的：通过对回归系数\beta与0的检验，看其是否有显著性差异，来判断回归系数是否显著。【检验系数是否显著】
调整R方
-
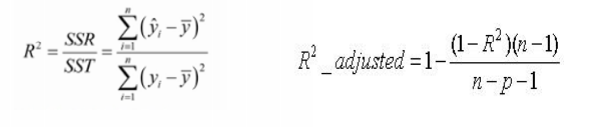
简单来说，使用R^2时，不断添加变量能让模型的效果看似提升，但这种提升是虚假的。
-
利用调整后的决定系数（adjusted r square），能对添加的非显著变量给出惩罚，即随意添加一个变量不一定能让模型拟合度上升。
注意：针对多元线性回归，调整R方效果更好
数据标准化
0~1标准化：
也叫离差标准化，是对原始数据的线性变换，使结果映射到[0,1]区间
Z标准化：
这种方法基于原始数据的均值和标准差进行数据的标准化。将A的原始值x使用z-score标准化到x'