
💡Yupureki:个人主页
🌸Yupureki🌸的简介:

目录
[1. 普通枚举](#1. 普通枚举)
[1.1 铺地毯](#1.1 铺地毯)
[1.2 回文日期](#1.2 回文日期)
[1.3 扫雷](#1.3 扫雷)
[2. 二进制枚举](#2. 二进制枚举)
[2.1 子集](#2.1 子集)
[2.2 费解的开关](#2.2 费解的开关)
前言
枚举,顾名思义,就是把所有可能的条件统统列出来并判断。因此这是个比较暴力的解法。如果数据范围较大,极有可能超时,因此我们常常需要优化算法,减少不必要的计算。
1. 普通枚举
1.1 铺地毯
题目链接:

算法原理
如果地毯覆盖某个点,那么我们按照初中数学学过的知识,其实就很容易推导出来
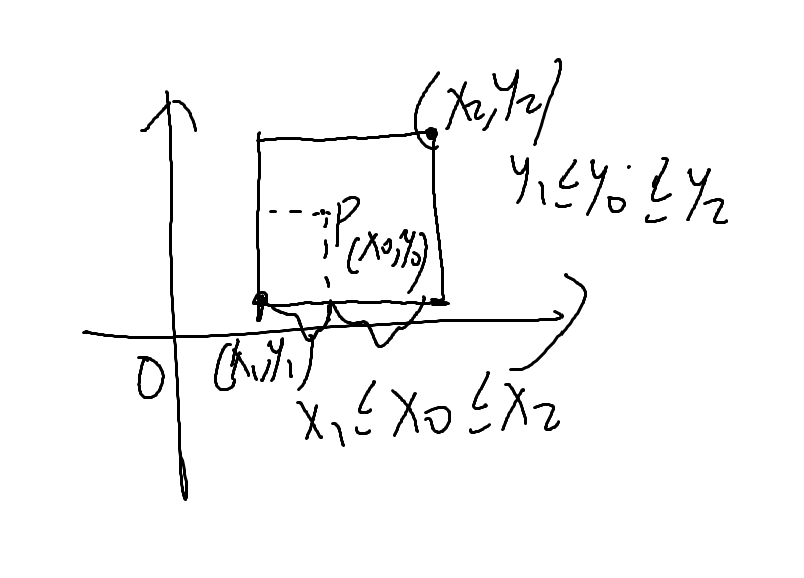
题目要我们找出最后一个覆盖的地毯,那么只需要从后往前遍历即可
实操代码
cpp
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int num;cin>>num;
vector<int> x(num),y(num),lx(num),ly(num);
for(int i = 0;i<num;i++)
{
cin>>x[i]>>y[i]>>lx[i]>>ly[i];
}
int n,m;cin>>n>>m;
for(int i = num-1;i>=0;i--)//从后往前遍历
{
if(n>=x[i] && n<=x[i] + lx[i] && m>=y[i] && m<=y[i] + ly[i])
{
cout<<i+1;
return 0;
}
}
cout<<"-1";
return 0;
}1.2 回文日期
题目链接:

算法原理
关于回文日期,其实就是回文字符串
所谓回文字符串,即一个字符串轴对称,例如"abba"是中间对称的,而"abab"则不是
那么对于日期,其实也就是个字符串,"20111102"是对称的,但"20121102"则不是对称的
随后题目要我们从两个日期之间,找出所有的回文日期的个数
咋一看,我们似乎需要从开始的日期一天天地数,直到最后的那天
从20000101开始
20000102...20000103.......20000201
真的需要这样吗?我们根据回文字符串的性质,我们假设前面四个字母已经确定了,就是2000,那么倒置过来就是0002,拼在一起就是20000002,所以前四个字母就已经确定了这四个字母开头的那个回文字符串,其余的皆不是。那么我们只需枚举年数即可。
当然如果得到的字符串如果压根不是个日期,例如20131302,直接干到13月去了,那么就不合适
实操代码
cpp
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
bool isleapyear(int year)//判断是否为闰年
{
if(year % 4 == 0)
{
if(year % 100 == 0)
{
if(year % 400 == 0)
return true;
else
return false;
}
else
return true;
}
else
return false;
}
int day[] = {31,28,31,30,31,30,31,31,30,31,30,31};//每个月的总天数
int getday(int year,int month)//拿到每个月的总天数
{
if(month == 2)
{
if(isleapyear(year))
return 29;
else
return 28;
}
else
return day[month-1];
}
int main()
{
string a, b; cin >> a >> b;
int count = 0;
int year1 = stoi(string(a.begin(), a.begin() + 4));
int year2 = stoi(string(b.begin(), b.begin() + 4));
int day1 = stoi(a); int day2 = stoi(b);
while (year1 <= year2)//枚举年数
{
string tmp = to_string(year1);
string tmp2 = tmp;
reverse(tmp2.begin(), tmp2.end());//反转年份(前4个字母)
tmp += tmp2;//由年份得到回文字符串
int date = stoi(tmp);//由字符串得到整型
if (date >= day1 && date <= day2)//判断是否是有效日期
{
int tmpday = date % 100;
date /= 100;
int tmpmonth = date % 100;
if (tmpmonth >= 1 && tmpmonth <= 12 && tmpday <= getday(year1, tmpmonth))
count++;
}
year1++;
}
cout << count;
return 0;
}1.3 扫雷
题目链接:

算法原理
第一眼,这个题目似乎枚举的种类好像还很多,也不好枚举,没事,我们由繁入简,从最简单的开始
对于下面的情况,我们假设第一个格子有雷
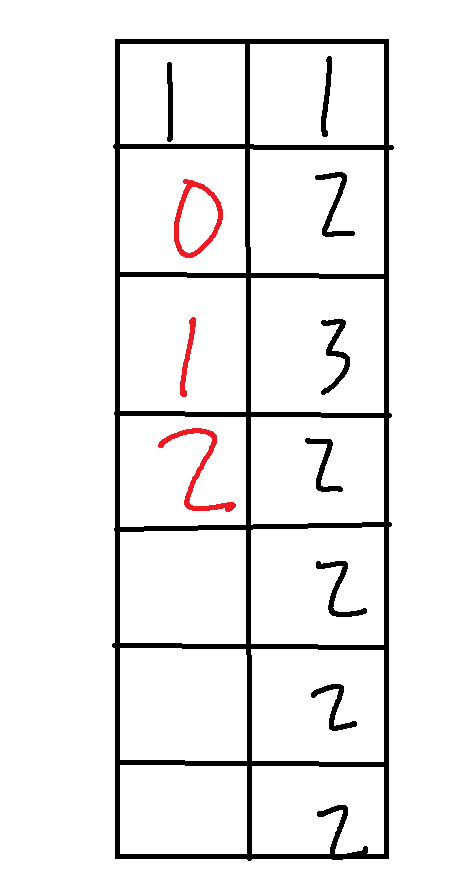
根据扫雷的性质,我们似乎可以一个一个往下推,推出后面每一个格子的雷的情况,推到后面发现有一个格子的雷数出现了2个,而一个格子有且仅有一个雷,因此这个情况不成立,当然如果雷数为负值也不成立
我们再假设第一个格子没有雷,也能顺理成章地推出来,是有解的
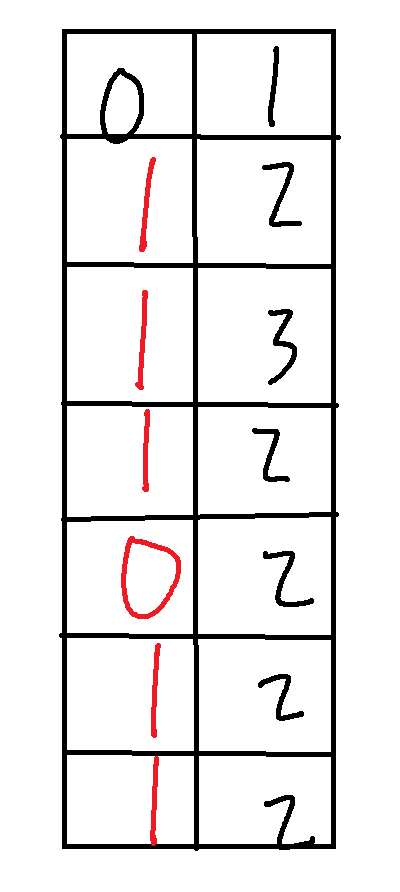
因此我们只需枚举第一个格子有没有雷即可
实操代码
cpp
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int n;cin>>n;
vector<int> a(n+2,0);vector<int> b(n+2,0);
for(int i = 1;i<=n+1;i++)
{
cin>>b[i];
}
int count = 0;
for(int i = 0;i<=1;i++)//枚举第一个格子有没有雷
{
a[1] = i;
int r = 1;
for(int j = 2;j<=n+1;j++)//递推
{
a[j] = b[j-1] - a[j-1] - a[j-2];
if(a[j]<0||a[j]>1)//雷数非法
{
r = 0;
break;
}
}
if(r && a[n+1] == 0)
count++;
}
cout<<count;
return 0;
}2. 二进制枚举
2.1 子集
题目链接:

算法原理
这个题目其实很像高中数学学的组合数学,即从一堆数种选多个数,问有多少种选法
那么这里我们引入一个新的算法技巧,即二进制枚举
在这里,nums有1,2,3 三个数,我们对于这三个数中的每一个数,要么选,要么不选
我们用1表示选,0表示不选
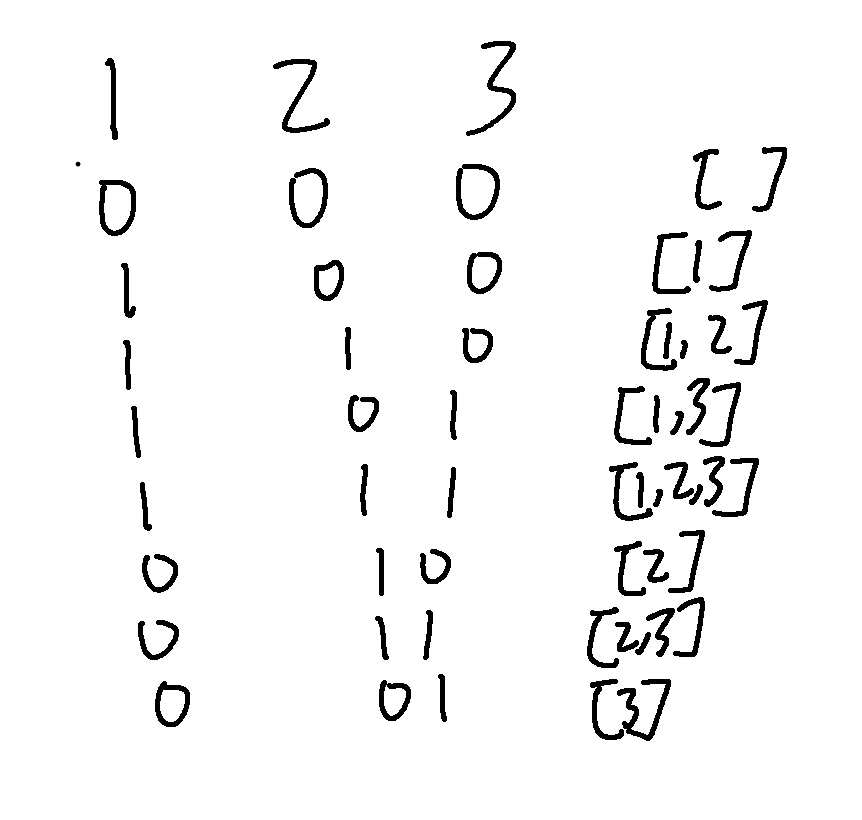
这个三个1和0组成的序列我们可以当作是某个数的二进制,如果我们观察从0到7,他们的二进制序列其实正好对应这所有的选择情况,因此这就是二进制序列
而这是三个数,2的3次方是8,从1到8-1的序列正好对应其所有的选择情况
因此我们可以把二进制枚举当作一个巧合,一个天才之举,巧妙地把0和1当作选和不选的情况
所以我们枚举从0 到2^n - 1的所有数的二进制枚举,把该数二进制的每一位当作选择的情况即可
实操代码
cpp
class Solution {
public:
vector<vector<int>> subsets(vector<int>& nums) {
int n = nums.size();
vector<vector<int>> ret;
for(int i = 0;i<(1<<n);i++)//枚举从0到2^n - 1的数
{
vector<int> tmp;
for(int j = 0;j<n;j++)
{
if((i>>j) & 1)//判断二进制的情况,如果是1,看作选择了对应这个位置的数
tmp.push_back(nums[j]);
}
ret.push_back(tmp);
}
return ret;
}
};2.2 费解的开关
题目链接:

算法原理
由于又是选与不选,因此我们也可以往二进制枚举那思考
我们先对第一行处理,我随便更改某些灯的状态
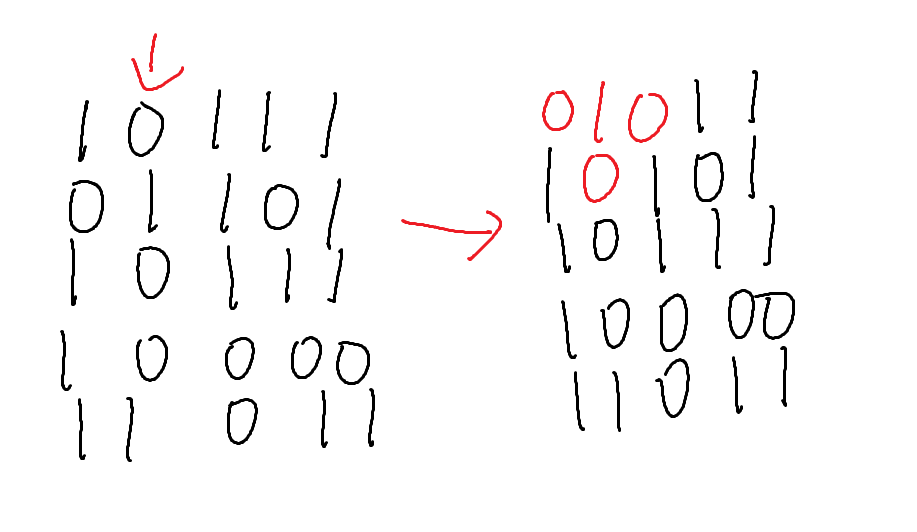
如果我们要使所有的灯都是亮着的,那么我们最起码得要前几行的灯是亮着的,那么第一行的灯就必须得亮着
所以我们对于第二行的改变只能是0下面的那些位置,这样就能让第一行的0变成1
同时你也不能改变其他的位置,因为这样就会更改第一行的1
以此类推,第三行,第四行,第五行的更改方式就是要把上一行的灯全变亮
所以当我们枚举,确定了第一行的更改状态,就会确定后面所有行的更改情况
最后确定第五行的灯是不是全亮的,以及操作次数是不是小于等于6的即可
到了具体代码上,我选择的是让一个数的二进制位表示这些灯的表示情况,由于有5行灯,为了防止越界访问,我们创造一个大小为6的数组 a[6],a[i]的二进制序列表示第i + 1行的灯的开关情况
这里也有个小细节,如果更改最左边的灯的情况,那么对应到二进制中,会改变第6位的数字,然而一行不存在6个灯。因此我们需要每一行修改后,a[i] &= (1<<5) - 1,这样会将第6位的数字改为0
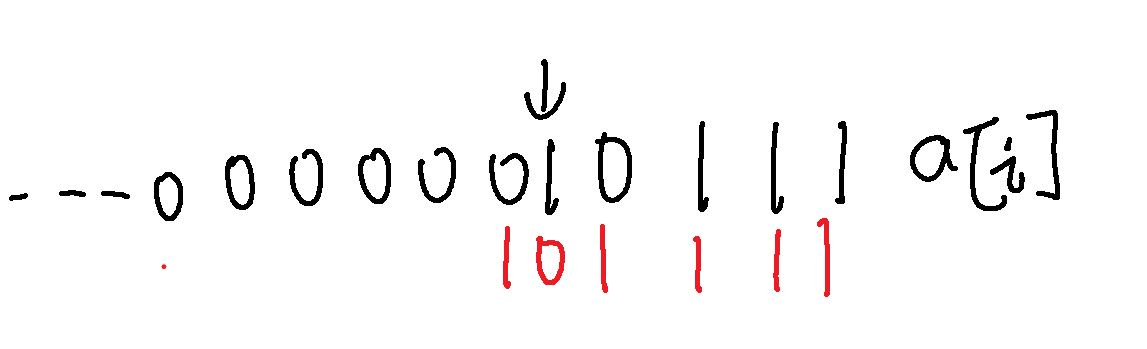
实操代码
cpp
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int group; cin >> group;
while (group--)
{
vector<int> a(6);//用一个数字的二进制表示每一行灯的 0 1状况
for (int j = 0; j < 5; j++)
{
for (int i = 1; i <= 5; i++)
{
char n; cin >> n;
if (n - '0' == 1)
a[j] |= (1 << (5 - i));
}
}
int min = 0xffffff;
for (int i = 0; i < (1 << 5); i++)
{
vector<int> b = a;
int push = i;//i的二进制序列的1表示选择,0表示不选,用push存储
int count = 0;
for (int j = 0; j < 5; j++)
{
for (int n = 0; n < 5; n++)
{
if (push & (1 << n))
count++;//统计改变次数
}
b[j] = b[j] ^ push ^ (push << 1) ^ (push >> 1);//改变这一行的状态
b[j] &= ((1 << 5) - 1);
b[j + 1] = b[j + 1] ^ push;//改变下一行的状态
push = b[j] ^ ((1 << 5) - 1);
}
if (b[4] == ((1 << 5) - 1) && count < min && count <= 6)
min = count;
}
if (min == 0xffffff)
cout << "-1" << endl;
else
cout << min << endl;
}
return 0;
}