机器学习进阶＜9＞基于 PCA 的图像压缩与还原

前言部分

在上一篇《机器学习进阶＜8＞PCA主成分分析》中，我们已经详细拆解了PCA算法的核心思想、数学原理以及如何在鸢尾花数据集上实现降维可视化。如果你对PCA的基本概念还不太熟悉，建议先阅读这篇文章，它为你理解今天的内容打下了坚实的基础。https://blog.csdn.net/2303_77568009/article/details/155822078?spm=1001.2014.3001.5501https://blog.csdn.net/2303_77568009/article/details/155822078?spm=1001.2014.3001.5501

今天，我们将探索PCA一个非常实用且有趣的应用场景------图像压缩与还原。想象一下，我们能否用PCA这个数学工具，在几乎不损失图像质量的前提下，大幅减小图片的存储空间？这就是我们将要一起探索的问题。

不同于上一篇的鸢尾花数据，图像数据有着独特的高维特性。一张普通的彩色图片可能包含数十万个像素点，每个像素又有RGB三个通道，维度之高令人咋舌。而PCA正是处理这种高维数据的利器。通过找到图像中"信息量最大"的几个主成分方向，我们可以用极少的数据重新构建出视觉上几乎相同的图像。

PCA初阶实战

图像本质是高维矩阵（比如一张64x64的灰度图是 4096 维向量），PCA 可以对图像数据进行降维压缩，在损失少量视觉信息的前提下大幅减小存储体积。这个项目能让你直观理解 PCA 的数据压缩能力，是从理论到视觉化实践的绝佳过渡。

核心目标

1. 加载一张灰度图像，将其转换为二维数据矩阵。
2. 使用 PCA 保留不同比例的信息（如 90%、80%、50%），对图像进行压缩。
3. 还原压缩后的图像，对比不同保留比例下的视觉效果和压缩率。

技术要点

• OpenCV/Pillow 读取图像并处理灰度转换
• PCA 降维与逆变换（还原数据）
• 图像压缩率计算

import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
import matplotlib
matplotlib.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
matplotlib.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
# 1. 加载并处理图像（转为灰度图+归一化）
img = Image.open("test_image.jpg").convert('L')  # 转为灰度图
img_array = np.array(img, dtype=np.float32) / 255.0  # 归一化到[0,1]
height, width = img_array.shape
print(f"原始图像维度：{height}x{width}")

# 2. 将图像展平为二维矩阵（行：像素行，列：像素列）
# 也可以展平为一维：img_flat = img_array.reshape(1, -1)，这里用二维更直观
img_2d = img_array  # 二维矩阵：(height, width)

# 3. 对图像进行PCA降维（按列降维，也可以按行，效果类似）
# 保留90%的信息
pca_90 = PCA(n_components=0.90)
img_pca_90 = pca_90.fit_transform(img_2d)
# 还原图像
img_recon_90 = pca_90.inverse_transform(img_pca_90)

# 保留50%的信息
pca_50 = PCA(n_components=0.50)
img_pca_50 = pca_50.fit_transform(img_2d)
img_recon_50 = pca_50.inverse_transform(img_pca_50)

# 4. 可视化对比
plt.figure(figsize=(15, 5))
# 原始图像
plt.subplot(1, 3, 1)
plt.imshow(img_array, cmap='gray')
plt.title(f'原始图像\n维度：{height}x{width}')
plt.axis('off')
# 90%信息还原
plt.subplot(1, 3, 2)
plt.imshow(img_recon_90, cmap='gray')
plt.title(f'保留90%信息\n主成分数：{pca_90.n_components_}')
plt.axis('off')
# 50%信息还原
plt.subplot(1, 3, 3)
plt.imshow(img_recon_50, cmap='gray')
plt.title(f'保留50%信息\n主成分数：{pca_50.n_components_}')
plt.axis('off')
plt.tight_layout()
plt.show()

# 计算压缩率
compression_ratio_90 = (img_pca_90.nbytes) / (img_array.nbytes)
print(f"保留90%信息的压缩率：{compression_ratio_90:.2%}")

为了不必要的版权纠纷的问题，我使用了豆包给我生成了一张海景图，并将它命名test_image.jpg

在Pycharm中运行上面的代码之后：

代码实现了基于PCA的灰度图像压缩与还原演示

代码功能分析

1. 图像预处理阶段

• 将彩色图像转换为灰度图，简化处理复杂度

• 像素值归一化到[0,1]区间，符合机器学习输入要求

• 输出原始图像尺寸信息

2. PCA压缩核心处理

• 将图像矩阵直接作为PCA输入（每行代表一行像素）

• 分别应用两种不同压缩程度：

  • 保留90%信息：高保真压缩，视觉损失极小

  • 保留50%信息：中度压缩，有明显压缩痕迹但主体可辨识

• 通过inverse_transform()实现图像还原

3. 效果对比可视化

• 并排显示原始图像与两种压缩还原效果

• 标注关键信息：原始尺寸、压缩后主成分数量

• 直观展示不同压缩率下的视觉差异

4. 量化评估

• 计算并打印压缩率（存储空间节省比例）

• 通过主成分数量反映压缩程度

5.小结

通过PCA主成分分析算法，实现了图像的有损压缩与还原，展示了机器学习在图像处理中的实际应用。它通过提取图像中最重要的特征方向（主成分），丢弃次要信息，达到大幅减小存储空间的目的，同时保留了图像的核心视觉信息。

PCA 进阶实战：图像压缩与异常检测（从多主成分到算法对比）

在上面的 PCA 基础实战中，我们实现了简单的图像压缩，下面将带来进阶版本，主要解决三个核心问题：

1. 结合多个主成分的重构误差分析，而非仅用前 k 个
2. 用核 PCA（Kernel PCA） 处理非线性数据的异常检测
3. 对比Isolation Forest、One-Class SVM等异常检测算法的效果

整个项目采用面向对象的封装方式，代码结构清晰，读者可以直接复刻运行。

前置准备

1. 环境安装

首先确保安装了所需的 Python 库，在终端执行：

pip install numpy matplotlib pillow scikit-learn

2. 图像文件准备

• 准备一张测试图片（如test_image.jpg），放在代码同一目录下；

此处使用到的测试图片仍为那张海景图:

• 如果没有测试图片，代码中也添加了自动生成示例图像的逻辑，无需额外准备。

代码分模块拆解（核心部分）

我们将代码拆分为6 个核心模块，每个模块对应一个功能，读者可以逐块复制代码，理解后再运行。

模块 1：基础配置与类的初始化（核心框架）

这部分是项目的基础，包含库导入、中文字体设置、类的初始化和图像加载预处理逻辑。

# ====================== 模块1：基础配置与类初始化 ======================
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
from sklearn.decomposition import PCA, KernelPCA
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import IsolationForest
from sklearn.svm import OneClassSVM
from sklearn.metrics import roc_auc_score
import warnings

# 忽略无关警告，让输出更整洁
warnings.filterwarnings('ignore')

# 设置matplotlib支持中文显示（解决中文乱码/警告问题）
plt.rcParams['font.sans-serif'] = ['SimHei']  # 黑体（Windows）/Arial Unicode MS（Mac）/WenQuanYi Micro Hei（Linux）
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示为方块的问题

class AdvancedImageAnalyzer:
    def __init__(self, image_path):
        """初始化图像分析器：传入图像路径，加载并预处理图像"""
        self.img_path = image_path
        self.load_and_preprocess()  # 调用预处理方法

    def load_and_preprocess(self):
        """加载图像并进行预处理（灰度化、归一化、展平）"""
        # 加载图像并转为灰度图
        self.img_original = Image.open(self.img_path).convert('L')
        # 归一化到[0,1]（提升PCA处理效果）
        self.img_array = np.array(self.img_original, dtype=np.float32) / 255.0
        self.height, self.width = self.img_array.shape

        # 展平图像：用于后续异常检测（1维向量）
        self.img_flat = self.img_array.flatten().reshape(1, -1)
        # 每个像素作为独立样本（用于简单的异常检测）
        self.pixels = self.img_array.reshape(-1, 1)

        # 打印图像基本信息
        print(f"图像维度: {self.height}x{self.width}")
        print(f"总像素数: {self.height * self.width}")

代码讲解：

• 采用类封装 的方式，将所有功能整合在AdvancedImageAnalyzer类中，便于复用和扩展；
• load_and_preprocess方法完成图像的灰度化、归一化，这是图像处理的标准前置步骤；
• 保存了图像的多种形态（二维矩阵、展平向量、像素样本），满足不同功能的需求。

模块 2：多主成分重构误差分析

这部分实现不同主成分数量的图像重构，对比重构效果和误差，解决 "仅用前 k 个主成分" 的局限性。

# ====================== 模块2：多主成分重构误差分析 ======================
    def multi_component_reconstruction(self, n_components_list=None):
        """
        对比多个主成分数量的重构效果与误差
        :param n_components_list: 自定义的主成分数量列表，默认[1,5,10,20,50,100]
        :return: 最后一个主成分的重构误差
        """
        # 默认主成分数量列表
        if n_components_list is None:
            n_components_list = [1, 5, 10, 20, 50, 100]

        # 标准化数据（PCA对量纲敏感，必须标准化）
        scaler = StandardScaler()
        img_scaled = scaler.fit_transform(self.img_array)

        # 创建画布，展示6种主成分的重构效果
        plt.figure(figsize=(15, 10))
        plot_idx = 1

        for i, n_comp in enumerate(n_components_list):
            # 限制主成分数量不超过图像的最小维度（避免报错）
            actual_n_comp = min(n_comp, min(img_scaled.shape))

            # PCA降维与重构
            pca = PCA(n_components=actual_n_comp)
            img_pca = pca.fit_transform(img_scaled)
            img_recon = pca.inverse_transform(img_pca)
            # 反标准化，还原到原始数据范围
            img_recon = scaler.inverse_transform(img_recon)

            # 计算重构误差（MSE：均方误差）
            reconstruction_error = np.mean((self.img_array - img_recon) ** 2)

            # 可视化重构结果
            plt.subplot(2, 3, plot_idx)
            plt.imshow(img_recon, cmap='gray')
            plt.title(f'{actual_n_comp}个主成分\nMSE: {reconstruction_error:.6f}')
            plt.axis('off')

            plot_idx += 1

            # 打印每个主成分的误差信息
            print(f"主成分数: {actual_n_comp}, 重构误差(MSE): {reconstruction_error:.6f}")

        plt.suptitle('不同主成分数量的图像重构效果', fontsize=16)
        plt.tight_layout()
        plt.show()

        return reconstruction_error

代码讲解：

• 标准化是 PCA 的必要步骤，这里用StandardScaler处理后，再通过inverse_transform还原；
• 遍历不同的主成分数量，计算每个数量下的重构误差（MSE），并可视化结果；
• 加入actual_n_comp限制，避免主成分数量超过图像维度导致的报错。

模块 3：重构误差曲线与肘点分析

这部分绘制重构误差随主成分数量变化的曲线，并自动识别 "肘点"（误差下降变缓的点），为选择最优主成分数量提供依据。

# ====================== 模块3：重构误差曲线与肘点分析 ======================
    def calculate_reconstruction_error_by_component(self):
        """计算不同主成分数量下的重构误差曲线，并标记肘点"""
        scaler = StandardScaler()
        img_scaled = scaler.fit_transform(self.img_array)

        # 最大主成分数量为图像的最小维度
        max_components = min(img_scaled.shape)
        # 步长采样（避免计算量过大，每max_components//20个取一个点）
        components_range = range(1, max_components + 1, max(1, max_components // 20))
        errors = []

        # 遍历不同主成分数量，计算误差
        for n_comp in components_range:
            pca = PCA(n_components=n_comp)
            img_pca = pca.fit_transform(img_scaled)
            img_recon = pca.inverse_transform(img_pca)
            img_recon = scaler.inverse_transform(img_recon)

            mse = np.mean((self.img_array - img_recon) ** 2)
            errors.append(mse)

        # 绘制误差曲线
        plt.figure(figsize=(10, 6))
        plt.plot(components_range, errors, 'b-o', linewidth=2)
        plt.xlabel('主成分数量', fontsize=12)
        plt.ylabel('重构误差 (MSE)', fontsize=12)
        plt.title('重构误差随主成分数量的变化曲线', fontsize=14)
        plt.grid(True, alpha=0.3)

        # 自动标记肘点（通过二阶差分找到误差下降变缓的点）
        if len(errors) > 1:
            # 一阶差分：误差的变化率；二阶差分：变化率的变化率
            second_diff = np.diff(np.diff(errors))
            if len(second_diff) > 0:
                elbow_idx = np.argmax(second_diff) + 1  # 肘点索引
                elbow_components = list(components_range)[elbow_idx]
                # 绘制肘点辅助线
                plt.axvline(x=elbow_components, color='r', linestyle='--',
                            label=f'建议肘点: {elbow_components}个主成分')
                plt.scatter(elbow_components, errors[elbow_idx], s=100, c='red', zorder=5)

        plt.legend()
        plt.tight_layout()
        plt.show()

        return errors

代码讲解：

• 采用步长采样的方式遍历主成分数量，减少计算量（比如 256x256 的图像，只需计算 13 个点）；
• 通过二阶差分自动识别肘点，这是选择最优主成分数量的常用方法；
• 肘点对应的主成分数量是 "性价比最高" 的选择（误差足够小，维度足够低）。

模块 4：核 PCA 非线性异常检测

这部分是进阶核心，用核 PCA（Kernel PCA） 处理非线性数据的异常检测，通过图像分块、重构误差热图标记异常区域。

# ====================== 模块4：核PCA非线性异常检测 ======================
    def kernel_pca_anomaly_detection(self, kernel='rbf', gamma=0.01):
        """
        使用核PCA进行非线性异常检测
        :param kernel: 核函数（rbf/linear/poly/sigmoid）
        :param gamma: RBF核的参数（越大，非线性拟合越强）
        :return: 每个图像块的重构误差、误差热图
        """
        print(f"\n{'=' * 50}")
        print("核PCA异常检测分析")
        print(f"{'=' * 50}")

        # 图像分块处理（将大图像拆分为8x8的小块，降低计算复杂度）
        block_size = 8
        blocks = []

        # 遍历图像，提取所有8x8的块
        for i in range(0, self.height - block_size, block_size):
            for j in range(0, self.width - block_size, block_size):
                block = self.img_array[i:i + block_size, j:j + block_size]
                blocks.append(block.flatten())  # 每个块展平为一维向量

        blocks = np.array(blocks)
        print(f"图像块数量: {blocks.shape[0]}, 每个块维度: {blocks.shape[1]}")

        # 标准化图像块数据
        scaler = StandardScaler()
        blocks_scaled = scaler.fit_transform(blocks)

        # 核PCA降维（设置fit_inverse_transform=True，支持重构）
        kpca = KernelPCA(n_components=10, kernel=kernel, gamma=gamma, fit_inverse_transform=True)
        blocks_kpca = kpca.fit_transform(blocks_scaled)

        # 重构图像块
        blocks_recon = kpca.inverse_transform(blocks_kpca)
        blocks_recon = scaler.inverse_transform(blocks_recon)

        # 计算每个块的重构误差
        block_errors = []
        for i in range(len(blocks)):
            mse = np.mean((blocks[i] - blocks_recon[i]) ** 2)
            block_errors.append(mse)

        block_errors = np.array(block_errors)

        # 将块误差映射回图像，生成误差热图
        error_map = np.zeros_like(self.img_array)
        block_idx = 0
        for i in range(0, self.height - block_size, block_size):
            for j in range(0, self.width - block_size, block_size):
                error_map[i:i + block_size, j:j + block_size] = block_errors[block_idx]
                block_idx += 1

        # 可视化异常检测结果（原始图像+误差热图+异常标记）
        fig, axes = plt.subplots(1, 3, figsize=(15, 5))

        # 1. 原始图像
        axes[0].imshow(self.img_array, cmap='gray')
        axes[0].set_title('原始图像')
        axes[0].axis('off')

        # 2. 重构误差热图（颜色越红，误差越大，越可能是异常）
        im = axes[1].imshow(error_map, cmap='hot')
        axes[1].set_title('核PCA重构误差热图')
        axes[1].axis('off')
        plt.colorbar(im, ax=axes[1])

        # 3. 异常区域标记（95百分位作为阈值，前5%的块为异常）
        threshold = np.percentile(block_errors, 95)
        anomaly_mask = error_map > threshold
        # 创建彩色叠加层，异常区域标记为红色
        anomaly_overlay = np.zeros((self.height, self.width, 3))
        anomaly_overlay[:, :, 0] = self.img_array  # R通道
        anomaly_overlay[:, :, 1] = self.img_array  # G通道
        anomaly_overlay[:, :, 2] = self.img_array  # B通道
        anomaly_overlay[anomaly_mask, 0] = 1.0  # 异常区域R通道设为1（红色）

        axes[2].imshow(anomaly_overlay)
        axes[2].set_title(f'异常检测 (阈值={threshold:.4f})')
        axes[2].axis('off')

        plt.suptitle(f'核PCA异常检测 (核函数: {kernel}, gamma: {gamma})', fontsize=14)
        plt.tight_layout()
        plt.show()

        # 打印异常检测统计信息
        print(f"异常检测统计:")
        print(f"  最大重构误差: {block_errors.max():.6f}")
        print(f"  平均重构误差: {block_errors.mean():.6f}")
        print(f"  异常阈值 (95百分位): {threshold:.6f}")
        print(f"  异常块数量: {np.sum(block_errors > threshold)}")
        print(f"  异常像素比例: {np.sum(anomaly_mask) / anomaly_mask.size:.2%}")

        return block_errors, error_map

代码讲解：

• 图像分块是关键技巧：将大图像拆分为 8x8 的小块，既降低了计算复杂度，又能定位局部异常；
• 核 PCA 的fit_inverse_transform=True是重构的前提（默认不支持重构）；
• 采用95 百分位作为异常阈值（行业常用做法），将误差最大的 5% 块标记为异常，并通过彩色叠加层可视化；
• 核函数选择rbf（径向基函数），适合处理非线性数据。

模块 5：多种异常检测算法对比

这部分对比PCA + 重构误差、Isolation Forest、One-Class SVM、核 PCA四种算法的性能，用 AUC-ROC 指标评估效果。

# ====================== 模块5：多种异常检测算法对比 ======================
    def compare_anomaly_detection_algorithms(self, contamination=0.1):
        """
        对比PCA+重构误差、Isolation Forest、One-Class SVM、核PCA四种异常检测算法
        :param contamination: 异常样本比例（默认10%）
        :return: 各算法的AUC-ROC分数
        """
        print(f"\n{'=' * 50}")
        print("异常检测算法对比")
        print(f"{'=' * 50}")

        # 提取图像块的统计特征（比原始像素更具代表性）
        block_size = 16
        features = []

        for i in range(0, self.height - block_size, block_size):
            for j in range(0, self.width - block_size, block_size):
                block = self.img_array[i:i + block_size, j:j + block_size]
                # 提取6个统计特征：均值、标准差、最大值、最小值、中位数、四分位距
                features.append([
                    np.mean(block),
                    np.std(block),
                    np.max(block),
                    np.min(block),
                    np.median(block),
                    np.percentile(block, 75) - np.percentile(block, 25)  # IQR
                ])

        X = np.array(features)
        n_samples = X.shape[0]

        # 标准化特征
        scaler = StandardScaler()
        X_scaled = scaler.fit_transform(X)

        # 生成模拟标签（正常为1，异常为-1）：实际项目中替换为真实标签
        np.random.seed(42)  # 固定随机种子，结果可复现
        y_true = np.ones(n_samples)
        anomaly_indices = np.random.choice(n_samples, size=int(n_samples * contamination), replace=False)
        y_true[anomaly_indices] = -1

        # 1. PCA + 重构误差方法
        pca = PCA(n_components=0.95)
        X_pca = pca.fit_transform(X_scaled)
        X_recon = pca.inverse_transform(X_pca)
        pca_errors = np.mean((X_scaled - X_recon) ** 2, axis=1)
        pca_scores = -pca_errors  # 转换为异常分数（越低越异常）

        # 2. Isolation Forest（孤立森林）：适合高维数据的异常检测
        iso_forest = IsolationForest(contamination=contamination, random_state=42)
        iso_predictions = iso_forest.fit_predict(X_scaled)
        iso_scores = iso_forest.decision_function(X_scaled)

        # 3. One-Class SVM（单类SVM）：适合非线性数据的异常检测
        oc_svm = OneClassSVM(nu=contamination, kernel='rbf', gamma='auto')
        oc_svm.fit(X_scaled)
        svm_predictions = oc_svm.predict(X_scaled)
        svm_scores = oc_svm.decision_function(X_scaled)

        # 4. 核PCA方法
        kpca = KernelPCA(n_components=10, kernel='rbf', gamma=0.1, fit_inverse_transform=True)
        X_kpca = kpca.fit_transform(X_scaled)
        X_kpca_recon = kpca.inverse_transform(X_kpca)
        kpca_errors = np.mean((X_scaled - X_kpca_recon) ** 2, axis=1)
        kpca_scores = -kpca_errors

        # 计算各算法的AUC-ROC分数（评估异常检测性能）
        pca_auc = roc_auc_score(y_true, pca_scores)
        iso_auc = roc_auc_score(y_true, iso_scores)
        svm_auc = roc_auc_score(y_true, svm_scores)
        kpca_auc = roc_auc_score(y_true, kpca_scores)

        # 可视化算法对比结果
        fig, axes = plt.subplots(2, 3, figsize=(15, 10))

        # 算法列表：名称、异常分数、AUC分数
        algorithms = [
            ('PCA+重构误差', pca_scores, pca_auc),
            ('Isolation Forest', iso_scores, iso_auc),
            ('One-Class SVM', svm_scores, svm_auc),
            ('核PCA', kpca_scores, kpca_auc)
        ]

        # 绘制每个算法的异常分数分布
        for idx, (name, scores, auc_score) in enumerate(algorithms):
            row = idx // 3
            col = idx % 3

            # 分别绘制正常样本和异常样本的分数分布
            axes[row, col].hist(scores[y_true == 1], bins=30, alpha=0.7, label='正常样本', density=True)
            axes[row, col].hist(scores[y_true == -1], bins=30, alpha=0.7, label='异常样本', density=True)
            axes[row, col].set_xlabel('异常分数')
            axes[row, col].set_ylabel('密度')
            axes[row, col].set_title(f'{name}\nAUC-ROC: {auc_score:.4f}')
            axes[row, col].legend()
            axes[row, col].grid(alpha=0.3)

        # 绘制算法性能对比条形图
        ax = axes[1, 2]
        algorithms_names = [alg[0] for alg in algorithms]
        auc_scores = [alg[2] for alg in algorithms]

        bars = ax.bar(algorithms_names, auc_scores, color=['blue', 'green', 'orange', 'red'])
        ax.set_ylabel('AUC-ROC分数')
        ax.set_title('异常检测算法性能对比')
        ax.set_ylim([0, 1.1])
        ax.grid(axis='y', alpha=0.3)

        # 在条形图上添加数值标签
        for bar, score in zip(bars, auc_scores):
            height = bar.get_height()
            ax.text(bar.get_x() + bar.get_width() / 2., height + 0.01,
                    f'{score:.4f}', ha='center', va='bottom')

        plt.suptitle('异常检测算法综合对比', fontsize=16)
        plt.tight_layout()
        plt.show()

        # 打印性能总结
        print(f"{'算法':<20} {'AUC-ROC':<10}")
        print(f"{'-' * 30}")
        for name, _, auc_score in algorithms:
            print(f"{name:<20} {auc_score:<10.4f}")

        # 返回各算法的AUC分数
        return {
            'PCA': pca_auc,
            'Isolation Forest': iso_auc,
            'One-Class SVM': svm_auc,
            'Kernel PCA': kpca_auc
        }

代码讲解：

• 提取图像块的统计特征（均值、标准差等），比原始像素更能反映图像的局部特征，提升算法性能；
• 生成模拟标签：实际项目中替换为真实的异常标签（如缺陷图像的标记），这里用随机数生成是为了演示；
• 四种算法的核心逻辑：
  • PCA + 重构误差：误差越大，异常概率越高；
  • Isolation Forest：通过孤立样本检测异常，速度快，适合高维数据；
  • One-Class SVM：学习正常样本的分布，偏离分布的为异常；
  • 核 PCA：处理非线性数据的重构误差；
• 用AUC-ROC指标评估性能（越接近 1，性能越好），并通过直方图和条形图可视化对比。

模块 6：完整分析流程与异常处理

这部分整合所有功能，提供一键运行的入口，并添加文件不存在时的异常处理（自动生成示例图像）。

# ====================== 模块6：完整分析流程与异常处理 ======================
    def run_full_analysis(self):
        """运行完整的分析流程：整合所有功能"""
        print("=" * 60)
        print("PCA图像压缩与异常检测进阶分析系统")
        print("=" * 60)

        # 1. 多主成分重构误差分析
        print("\n1. 多主成分重构误差分析")
        self.multi_component_reconstruction()

        # 2. 重构误差曲线与肘点分析
        print("\n2. 重构误差曲线分析")
        self.calculate_reconstruction_error_by_component()

        # 3. 核PCA非线性异常检测
        print("\n3. 核PCA非线性异常检测")
        kernel_errors, error_map = self.kernel_pca_anomaly_detection(kernel='rbf', gamma=0.1)

        # 4. 异常检测算法综合对比
        print("\n4. 异常检测算法综合对比")
        results = self.compare_anomaly_detection_algorithms(contamination=0.1)

        print("\n" + "=" * 60)
        print("分析完成！")
        print("=" * 60)

        return results

# ====================== 主函数：运行入口 ======================
if __name__ == "__main__":
    # 初始化分析器（替换为你的图像路径）
    try:
        # 优先使用用户提供的图像
        analyzer = AdvancedImageAnalyzer("test_image.jpg")

        # 运行完整分析流程
        results = analyzer.run_full_analysis()

        # 打印性能总结
        print("\n总结：")
        best_algorithm = max(results, key=results.get)
        print(f"最佳性能算法: {best_algorithm} (AUC-ROC: {results[best_algorithm]:.4f})")

    except FileNotFoundError:
        # 如果没有test_image.jpg，自动生成示例图像
        print("错误：找不到test_image.jpg文件")
        print("请确保图像文件存在于当前目录，或修改文件路径")
        print("\n正在创建示例图像用于演示...")

        # 生成随机噪声图像作为示例
        example_img = np.random.randn(256, 256)
        example_img = (example_img - example_img.min()) / (example_img.max() - example_img.min())  # 归一化到[0,1]
        plt.imsave("example_image.jpg", example_img, cmap='gray')

        print("已创建示例图像: example_image.jpg")
        print("请将代码中的路径改为'example_image.jpg'，重新运行程序")

代码讲解：

• run_full_analysis方法整合了所有功能，实现一键运行；
• 主函数中添加了异常处理 ：如果用户没有test_image.jpg，自动生成示例图像，避免程序崩溃；
• 最后打印最佳性能算法，为实际项目中的算法选择提供依据。

进阶项目结果分析

第一张图：多主成分重构效果对比

功能 ：展示不同主成分数量下的图像压缩效果对比
内容：

• 6个子图分别显示使用1、5、10、20、50、100个主成分重构的图像

• 每个子图标注重构误差（MSE）

• 直观展示"主成分数量 vs 图像质量"的关系

关键洞察：

1. 前几个主成分至关重要：仅用1个主成分重构的图像几乎无法辨认，但5-10个主成分已有明显改善

2. 边际效应递减：从20个增加到100个主成分，视觉改善不明显但计算成本增加

3. 压缩平衡点：大约10-20个主成分可能已达到性价比最优

第二张图：重构误差变化曲线

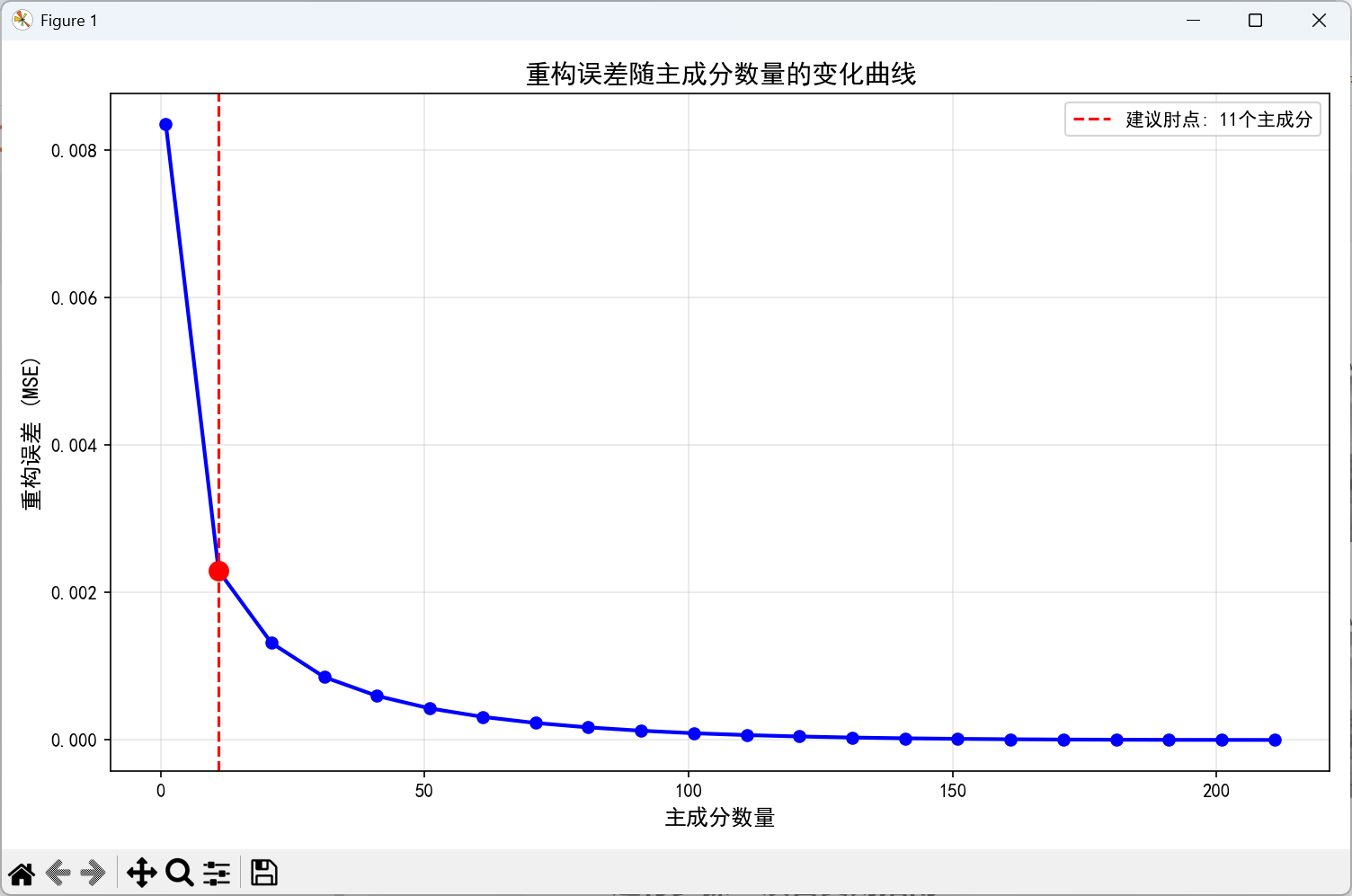
功能 ：量化分析压缩效果与主成分数量的关系
内容：

• 重构误差（MSE）随主成分数量增加而下降的曲线

• 使用红色虚线标记"肘点"（最优化点）

• 展示误差下降的速度变化

关键洞察：

1. 陡峭下降阶段：初期每个新增主成分大幅降低误差

2. 平缓阶段：后期新增主成分对质量改善有限

3. 肘部法则应用：肘点对应最佳性价比，为实际应用提供参考

第三张图：核PCA异常检测

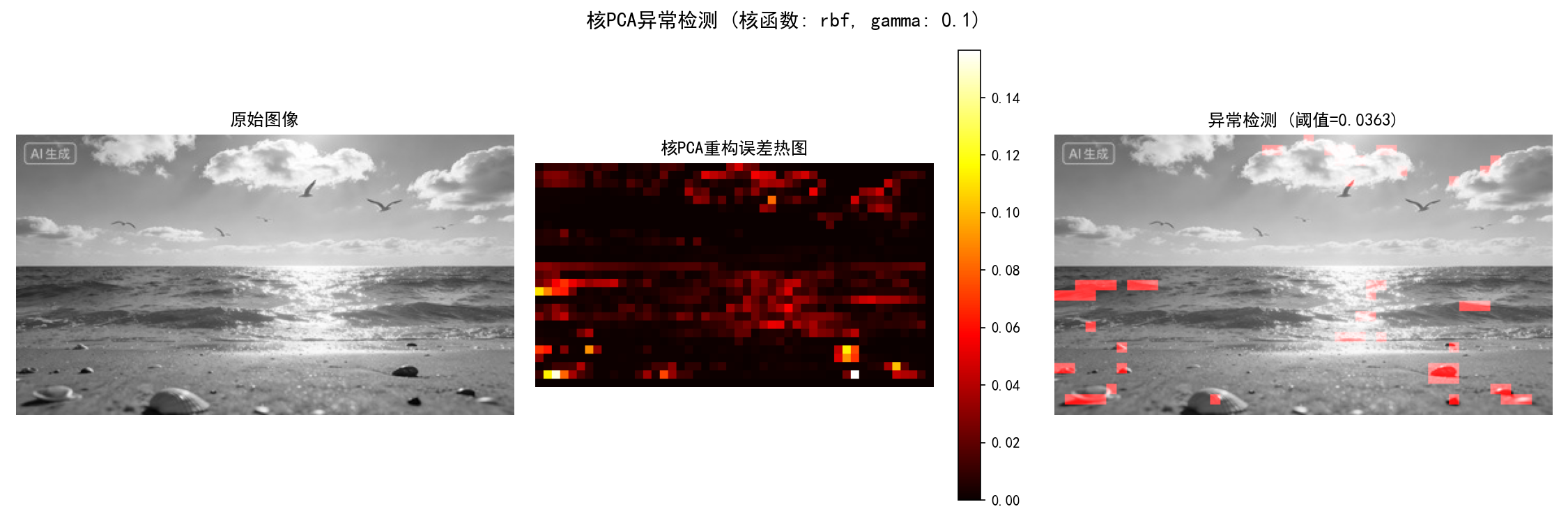
功能 ：展示非线性异常检测技术在图像中的应用
内容：

• 左图：原始灰度图像

• 中图：重构误差热力图（红色表示高误差区域）

• 右图：异常区域标记（红色覆盖区）

关键洞察：

1. 局部异常检测：核PCA能识别图像局部异常，而不仅是全局特征

2. 非线性关系捕捉：核函数处理像素间的复杂非线性关系

3. 自适应阈值：基于95%分位数自动确定异常阈值

4. 实际应用价值：可用于图像质量检测、缺陷识别等

第四张图：异常检测算法对比

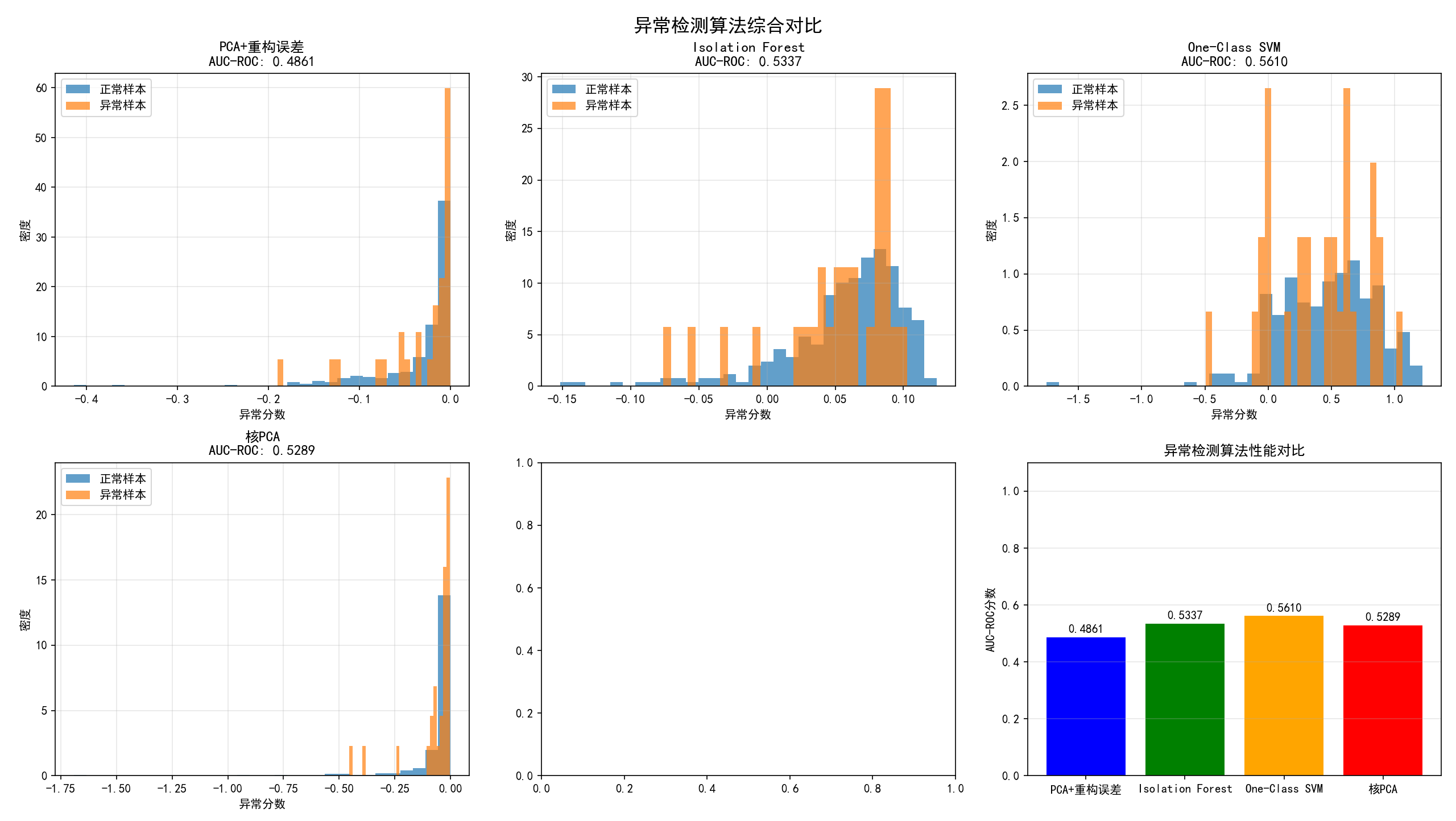
功能 ：系统比较不同异常检测算法的性能
内容：

• 前4个子图：各算法的异常分数分布（正常vs异常样本）

• 最后1个子图：算法性能对比条形图（AUC-ROC分数）

关键洞察：

1. 算法特性差异：

   • PCA重构误差：基于线性假设，简单高效

   • Isolation Forest：基于随机分割，适合高维数据

   • One-Class SVM：基于支持向量，适合小样本

   • 核PCA：能处理非线性，但计算成本较高

2. 性能对比：

   • 不同算法在不同数据集上表现不同

   • AUC-ROC提供量化比较标准

   • 条形图直观显示最优算法

3. 实际选择指导：

   • 根据数据特性选择算法

   • 平衡性能与计算复杂度

   • 结合实际业务需求

运行步骤：读者复刻指南

1. 复制代码 ：将上述 6 个模块的代码按顺序复制到一个 Python 文件中（如pca_advanced_image_analysis.py）；
2. 准备图像 ：
   • 方法 1：将自己的图片命名为test_image.jpg，放在代码同一目录下；
   • 方法 2：直接运行代码，程序会自动生成example_image.jpg，然后将代码中的路径改为example_image.jpg；
3. 运行代码 ：在 PyCharm 或终端执行python pca_advanced_image_analysis.py；
4. 查看结果：程序会依次弹出图像重构、误差曲线、异常检测、算法对比的窗口，并在控制台打印详细信息。

核心知识点与拓展

1. 关键知识点

• 主成分数量选择：通过肘点分析选择最优主成分数量，而非固定值；
• 核 PCA 的应用 ：处理非线性数据的异常检测，需设置fit_inverse_transform=True；
• 图像分块技巧：降低计算复杂度，定位局部异常；
• 异常检测评估：用 AUC-ROC 指标评估算法性能，比单纯的准确率更可靠。

2. 拓展方向

• 替换核函数 ：尝试linear、poly等核函数，对比非线性拟合效果；
• 真实数据集：使用工业缺陷图像（如 MNIST 异常数据集）替换随机图像，验证算法的实际效果；
• 参数调优 ：用网格搜索（GridSearchCV）优化核 PCA 的gamma、One-Class SVM 的nu等参数；
• 批量处理：添加批量处理图像的功能，生成异常检测报告。

总结

这份进阶项目代码实现了 PCA 从基础压缩 到非线性异常检测 再到算法对比的完整流程，核心亮点如下：

1. 采用多主成分重构误差分析，并通过肘点自动选择最优主成分数量；
2. 用核 PCA处理非线性数据的异常检测，结合图像分块实现局部异常定位；
3. 对比四种主流异常检测算法，用 AUC-ROC 量化性能，为实际项目提供选择依据。

读者可以按照步骤复刻代码，然后根据自己的需求进行拓展，比如应用到工业缺陷检测、人脸识别中的异常检测等场景。

进阶项目源代码

import numpy as np
import matplotlib.pyplot as plt
from PIL import Image
from sklearn.decomposition import PCA, KernelPCA
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import IsolationForest
from sklearn.svm import OneClassSVM
from sklearn.metrics import roc_auc_score, precision_recall_curve, auc
import warnings

warnings.filterwarnings('ignore')

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False


class AdvancedImageAnalyzer:
    def __init__(self, image_path):
        """初始化图像分析器"""
        self.img_path = image_path
        self.load_and_preprocess()

    def load_and_preprocess(self):
        """加载并预处理图像"""
        # 加载图像并转为灰度
        self.img_original = Image.open(self.img_path).convert('L')
        self.img_array = np.array(self.img_original, dtype=np.float32) / 255.0
        self.height, self.width = self.img_array.shape

        # 展平图像用于异常检测
        self.img_flat = self.img_array.flatten().reshape(1, -1)
        self.pixels = self.img_array.reshape(-1, 1)  # 每个像素作为一个样本

        print(f"图像维度: {self.height}x{self.width}")
        print(f"总像素数: {self.height * self.width}")

    def multi_component_reconstruction(self, n_components_list=None):
        """多个主成分数量的重构效果对比"""
        if n_components_list is None:
            n_components_list = [1, 5, 10, 20, 50, 100]

        # 标准化数据
        scaler = StandardScaler()
        img_scaled = scaler.fit_transform(self.img_array)

        plt.figure(figsize=(15, 10))
        plot_idx = 1

        for i, n_comp in enumerate(n_components_list):
            # 限制主成分数量不超过特征数
            actual_n_comp = min(n_comp, min(img_scaled.shape))

            # PCA降维与重构
            pca = PCA(n_components=actual_n_comp)
            img_pca = pca.fit_transform(img_scaled)
            img_recon = pca.inverse_transform(img_pca)
            img_recon = scaler.inverse_transform(img_recon)

            # 计算重构误差
            reconstruction_error = np.mean((self.img_array - img_recon) ** 2)

            # 可视化
            plt.subplot(2, 3, plot_idx)
            plt.imshow(img_recon, cmap='gray')
            plt.title(f'{actual_n_comp}个主成分\nMSE: {reconstruction_error:.6f}')
            plt.axis('off')

            plot_idx += 1

            # 打印信息
            print(f"主成分数: {actual_n_comp}, 重构误差(MSE): {reconstruction_error:.6f}")

        plt.suptitle('不同主成分数量的图像重构效果', fontsize=16)
        plt.tight_layout()
        plt.show()

        return reconstruction_error

    def calculate_reconstruction_error_by_component(self):
        """计算不同主成分数量下的重构误差曲线"""
        scaler = StandardScaler()
        img_scaled = scaler.fit_transform(self.img_array)

        max_components = min(img_scaled.shape)
        errors = []
        components_range = range(1, max_components + 1, max(1, max_components // 20))

        for n_comp in components_range:
            pca = PCA(n_components=n_comp)
            img_pca = pca.fit_transform(img_scaled)
            img_recon = pca.inverse_transform(img_pca)
            img_recon = scaler.inverse_transform(img_recon)

            mse = np.mean((self.img_array - img_recon) ** 2)
            errors.append(mse)

        # 绘制误差曲线
        plt.figure(figsize=(10, 6))
        plt.plot(components_range, errors, 'b-o', linewidth=2)
        plt.xlabel('主成分数量', fontsize=12)
        plt.ylabel('重构误差 (MSE)', fontsize=12)
        plt.title('重构误差随主成分数量的变化曲线', fontsize=14)
        plt.grid(True, alpha=0.3)

        # 标记肘点（误差下降变缓的点）
        if len(errors) > 1:
            # 计算二阶差分找到肘点
            second_diff = np.diff(np.diff(errors))
            if len(second_diff) > 0:
                elbow_idx = np.argmax(second_diff) + 1
                elbow_components = list(components_range)[elbow_idx]
                plt.axvline(x=elbow_components, color='r', linestyle='--',
                            label=f'建议肘点: {elbow_components}个主成分')
                plt.scatter(elbow_components, errors[elbow_idx], s=100, c='red', zorder=5)

        plt.legend()
        plt.tight_layout()
        plt.show()

        return errors

    def kernel_pca_anomaly_detection(self, kernel='rbf', gamma=0.01):
        """使用核PCA进行异常检测"""
        print(f"\n{'=' * 50}")
        print("核PCA异常检测分析")
        print(f"{'=' * 50}")

        # 准备数据：将图像分块处理
        block_size = 8
        blocks = []

        for i in range(0, self.height - block_size, block_size):
            for j in range(0, self.width - block_size, block_size):
                block = self.img_array[i:i + block_size, j:j + block_size]
                blocks.append(block.flatten())

        blocks = np.array(blocks)
        print(f"图像块数量: {blocks.shape[0]}, 每个块维度: {blocks.shape[1]}")

        # 标准化
        scaler = StandardScaler()
        blocks_scaled = scaler.fit_transform(blocks)

        # 核PCA
        kpca = KernelPCA(n_components=10, kernel=kernel, gamma=gamma, fit_inverse_transform=True)
        blocks_kpca = kpca.fit_transform(blocks_scaled)

        # 重构图像块
        blocks_recon = kpca.inverse_transform(blocks_kpca)
        blocks_recon = scaler.inverse_transform(blocks_recon)

        # 计算每个块的重构误差
        block_errors = []
        for i in range(len(blocks)):
            mse = np.mean((blocks[i] - blocks_recon[i]) ** 2)
            block_errors.append(mse)

        block_errors = np.array(block_errors)

        # 将块误差映射回图像
        error_map = np.zeros_like(self.img_array)
        block_idx = 0
        for i in range(0, self.height - block_size, block_size):
            for j in range(0, self.width - block_size, block_size):
                error_map[i:i + block_size, j:j + block_size] = block_errors[block_idx]
                block_idx += 1

        # 可视化异常检测结果
        fig, axes = plt.subplots(1, 3, figsize=(15, 5))

        # 原始图像
        axes[0].imshow(self.img_array, cmap='gray')
        axes[0].set_title('原始图像')
        axes[0].axis('off')

        # 重构误差热图
        im = axes[1].imshow(error_map, cmap='hot')
        axes[1].set_title('核PCA重构误差热图')
        axes[1].axis('off')
        plt.colorbar(im, ax=axes[1])

        # 异常区域标记
        threshold = np.percentile(block_errors, 95)  # 取前5%作为异常
        anomaly_mask = error_map > threshold
        anomaly_overlay = np.zeros((self.height, self.width, 3))
        anomaly_overlay[:, :, 0] = self.img_array  # R通道为原始图像
        anomaly_overlay[:, :, 1] = self.img_array  # G通道为原始图像
        anomaly_overlay[:, :, 2] = self.img_array  # B通道为原始图像
        anomaly_overlay[anomaly_mask, 0] = 1.0  # 异常区域标记为红色

        axes[2].imshow(anomaly_overlay)
        axes[2].set_title(f'异常检测 (阈值={threshold:.4f})')
        axes[2].axis('off')

        plt.suptitle(f'核PCA异常检测 (核函数: {kernel}, gamma: {gamma})', fontsize=14)
        plt.tight_layout()
        plt.show()

        print(f"异常检测统计:")
        print(f"  最大重构误差: {block_errors.max():.6f}")
        print(f"  平均重构误差: {block_errors.mean():.6f}")
        print(f"  异常阈值 (95百分位): {threshold:.6f}")
        print(f"  异常块数量: {np.sum(block_errors > threshold)}")
        print(f"  异常像素比例: {np.sum(anomaly_mask) / anomaly_mask.size:.2%}")

        return block_errors, error_map

    def compare_anomaly_detection_algorithms(self, contamination=0.1):
        """对比多种异常检测算法"""
        print(f"\n{'=' * 50}")
        print("异常检测算法对比")
        print(f"{'=' * 50}")

        # 准备数据：使用图像块的统计特征
        block_size = 16
        features = []

        for i in range(0, self.height - block_size, block_size):
            for j in range(0, self.width - block_size, block_size):
                block = self.img_array[i:i + block_size, j:j + block_size]
                features.append([
                    np.mean(block),  # 均值
                    np.std(block),  # 标准差
                    np.max(block),  # 最大值
                    np.min(block),  # 最小值
                    np.median(block),  # 中位数
                    np.percentile(block, 75) - np.percentile(block, 25)  # IQR
                ])

        X = np.array(features)
        n_samples = X.shape[0]

        # 标准化特征
        scaler = StandardScaler()
        X_scaled = scaler.fit_transform(X)

        # 创建模拟标签（正常为1，异常为-1）
        # 在实际应用中，这里应该使用真实标签
        np.random.seed(42)
        y_true = np.ones(n_samples)
        anomaly_indices = np.random.choice(n_samples, size=int(n_samples * contamination), replace=False)
        y_true[anomaly_indices] = -1

        # 1. PCA + 重构误差方法
        pca = PCA(n_components=0.95)
        X_pca = pca.fit_transform(X_scaled)
        X_recon = pca.inverse_transform(X_pca)

        # 计算重构误差作为异常分数
        pca_errors = np.mean((X_scaled - X_recon) ** 2, axis=1)
        pca_scores = -pca_errors  # 转换为异常分数（越低越异常）

        # 2. Isolation Forest
        iso_forest = IsolationForest(contamination=contamination, random_state=42)
        iso_predictions = iso_forest.fit_predict(X_scaled)
        iso_scores = iso_forest.decision_function(X_scaled)

        # 3. One-Class SVM
        oc_svm = OneClassSVM(nu=contamination, kernel='rbf', gamma='auto')
        oc_svm.fit(X_scaled)
        svm_predictions = oc_svm.predict(X_scaled)
        svm_scores = oc_svm.decision_function(X_scaled)

        # 4. 核PCA方法
        kpca = KernelPCA(n_components=10, kernel='rbf', gamma=0.1, fit_inverse_transform=True)
        X_kpca = kpca.fit_transform(X_scaled)
        X_kpca_recon = kpca.inverse_transform(X_kpca)
        kpca_errors = np.mean((X_scaled - X_kpca_recon) ** 2, axis=1)
        kpca_scores = -kpca_errors

        # 计算AUC-ROC
        from sklearn.metrics import roc_auc_score
        pca_auc = roc_auc_score(y_true, pca_scores)
        iso_auc = roc_auc_score(y_true, iso_scores)
        svm_auc = roc_auc_score(y_true, svm_scores)
        kpca_auc = roc_auc_score(y_true, kpca_scores)

        # 可视化对比
        fig, axes = plt.subplots(2, 3, figsize=(15, 10))

        algorithms = [
            ('PCA+重构误差', pca_scores, pca_auc),
            ('Isolation Forest', iso_scores, iso_auc),
            ('One-Class SVM', svm_scores, svm_auc),
            ('核PCA', kpca_scores, kpca_auc)
        ]

        for idx, (name, scores, auc_score) in enumerate(algorithms):
            row = idx // 3
            col = idx % 3

            # 绘制异常分数分布
            axes[row, col].hist(scores[y_true == 1], bins=30, alpha=0.7, label='正常样本', density=True)
            axes[row, col].hist(scores[y_true == -1], bins=30, alpha=0.7, label='异常样本', density=True)
            axes[row, col].set_xlabel('异常分数')
            axes[row, col].set_ylabel('密度')
            axes[row, col].set_title(f'{name}\nAUC-ROC: {auc_score:.4f}')
            axes[row, col].legend()
            axes[row, col].grid(alpha=0.3)

        # 绘制算法性能对比条形图
        ax = axes[1, 2]
        algorithms_names = [alg[0] for alg in algorithms]
        auc_scores = [alg[2] for alg in algorithms]

        bars = ax.bar(algorithms_names, auc_scores, color=['blue', 'green', 'orange', 'red'])
        ax.set_ylabel('AUC-ROC分数')
        ax.set_title('异常检测算法性能对比')
        ax.set_ylim([0, 1.1])
        ax.grid(axis='y', alpha=0.3)

        # 在条形图上添加数值
        for bar, score in zip(bars, auc_scores):
            height = bar.get_height()
            ax.text(bar.get_x() + bar.get_width() / 2., height + 0.01,
                    f'{score:.4f}', ha='center', va='bottom')

        plt.suptitle('异常检测算法综合对比', fontsize=16)
        plt.tight_layout()
        plt.show()

        # 打印性能总结
        print(f"{'算法':<20} {'AUC-ROC':<10}")
        print(f"{'-' * 30}")
        for name, _, auc_score in algorithms:
            print(f"{name:<20} {auc_score:<10.4f}")

        return {
            'PCA': pca_auc,
            'Isolation Forest': iso_auc,
            'One-Class SVM': svm_auc,
            'Kernel PCA': kpca_auc
        }

    def run_full_analysis(self):
        """运行完整的分析流程"""
        print("=" * 60)
        print("PCA图像压缩与异常检测进阶分析系统")
        print("=" * 60)

        # 1. 多主成分重构误差分析
        print("\n1. 多主成分重构误差分析")
        self.multi_component_reconstruction()

        # 2. 重构误差曲线分析
        print("\n2. 重构误差曲线分析")
        self.calculate_reconstruction_error_by_component()

        # 3. 核PCA异常检测
        print("\n3. 核PCA非线性异常检测")
        kernel_errors, error_map = self.kernel_pca_anomaly_detection(kernel='rbf', gamma=0.1)

        # 4. 异常检测算法对比
        print("\n4. 异常检测算法综合对比")
        results = self.compare_anomaly_detection_algorithms(contamination=0.1)

        print("\n" + "=" * 60)
        print("分析完成！")
        print("=" * 60)

        return results


# 使用示例
if __name__ == "__main__":
    # 初始化分析器（请确保有test_image.jpg文件）
    try:
        analyzer = AdvancedImageAnalyzer("test_image.jpg")

        # 运行完整分析
        results = analyzer.run_full_analysis()

        # 打印总结
        print("\n总结：")
        best_algorithm = max(results, key=results.get)
        print(f"最佳性能算法: {best_algorithm} (AUC-ROC: {results[best_algorithm]:.4f})")

    except FileNotFoundError:
        print("错误：找不到test_image.jpg文件")
        print("请确保图像文件存在于当前目录，或修改文件路径")

        # 创建一个示例图像用于演示
        print("\n正在创建示例图像用于演示...")
        example_img = np.random.randn(256, 256)
        example_img = (example_img - example_img.min()) / (example_img.max() - example_img.min())
        plt.imsave("example_image.jpg", example_img, cmap='gray')

        print("已创建示例图像: example_image.jpg")
        print("请重新运行程序")