基本信息

解决的问题
核心问题
如何将 "目标之间的时间依赖性"(Temporal Dependencies among Targets, TDT) 整合到
"非自回归"(Non-Autoregressive, NAR)时间序列预测模型中,从而在保持高效率 的同时提高预测的有效性。
论文指出了现有方法在效率 和有效性之间的权衡问题。
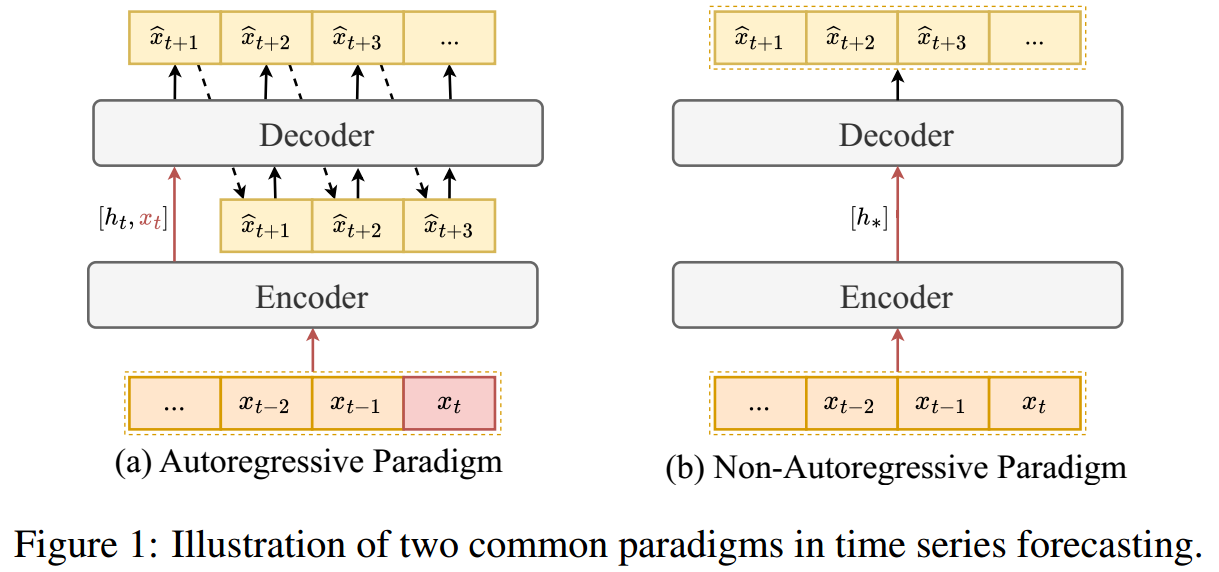
自回归(Autoregressive, AR)方法的局限性
- AR 方法(如 LSTM、GRU、DeepAR 等)通过递归地、一步一步地进行预测,能够对 "目标序列之间的时间依赖性(TDT)" 进行建模,从而提高建模准确性(有效性) 。
- 但是,这种递归结构会导致预测推理效率低下 (速度慢),并且在长期预测中容易出现误差积累和传播,从而降低预测质量 。
非自回归(Non-Autoregressive, NAR)方法的局限性
-
NAR 方法(如 DLinear、PatchTST 等)可以直接一步到位地输出多步预测结果,极大地提高了预测效率 。
-
然而,NAR 方法通常**忽略了预测目标序列之间的时间依赖性(TDT),**虽然一些方法尝试通过位置编码或时间戳隐式地捕获时间顺序,但对于 TDT 的全面探索和显式学习仍然不足 。
因此,论文的动机在于寻求一种结合两者优势的解决方案:
目标: 结合 AR 和 NAR 的优势,实现更有效且更高效的时间序列预测 。
关键: 对预测序列中 目标之间的时间依赖性(TDT) 进行建模和利用 。
为解决这个问题,论文提出了 TDT Loss (Temporal Dependencies among Targets Loss) 这种优化目标 。这是一个无需参数、即插即用的解决方案,旨在引导非自回归模型动态地关注目标值预测和 TDT 学习,从而在保持 NAR 效率的同时,提升其预测性能 。
提出的方法
Temporal Dependencies among Targets (TDT)
Importance of TDT
时间序列具有时间顺序的属性,每个时间步的观测值都会受到前一个时间步观测值的影响。
模型捕捉TDT的能力也可以反映其预测目标的准确性,模型对相邻时间步之间的 递增或递减关系 以及具体 递增或递减值的预测不准确,本质上是目标值预测不准确的表现,反之,当模型达到较好的目标预测性能时,它在捕获TDT方面也表现出上级性能。
Representation of TDT
为了让非自回归模型能够学习 TDT,论文首先提供了一个具体且直观的 TDT 表示方法,即一阶差分法(First-order Differencing)
- TDT 序列
的定义: TDT 序列
是预测序列
中相邻时间步之间的差值 。
其中 是历史序列的最后一个观测值。
-
TDT 的双重粒度: 这种表示方法能够捕获 TDT 的两种粒度信息
-
细粒度 TDT:
的值量化了相邻时间步之间的具体增量或减量 。
-
粗粒度 TDT :
的符号指示了相邻时间步之间是递增还是递减的关系 。
-
-
选择原因: 论文选择一阶差分(
)而非高阶差分,是基于时间序列普遍存在的临近性 (proximity)原则,即相邻时间步具有最强的依赖关系 。这保证了模型能够捕获核心 的、易于学习的依赖信息,同时避免了高阶差分可能带来的计算复杂性增加和过度约束问题 。
TDT Loss: Guiding Non-Autoregressive Models to Learn TDT
NAR基模型存在两个主要限制:第一,基础模型的结构设计缺乏TDT的显式建模 。第二,基础模型中常用的优化目标未能优化TDT的学习。
为应对上述挑战,本文提出TDT Loss:
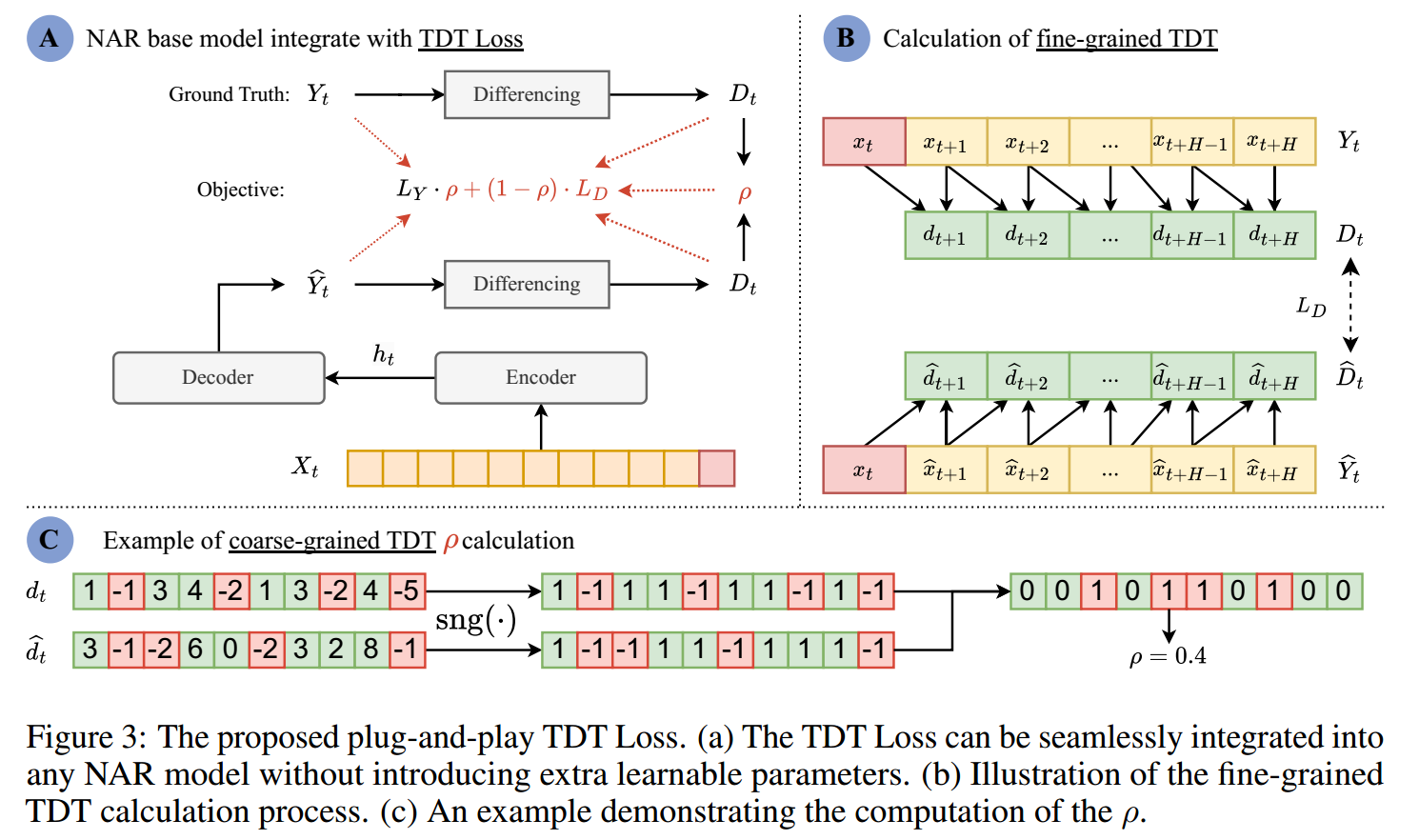
目标预测损失 ( )
)
常用的预测损失,衡量预测值 与真实值
之间的差异 。
(其中 是 MSE 或 MAE 等距离度量 。)
TDT 值预测损失 ( )
)
-
衡量模型拟合细粒度 TDT(即具体的增量或减量值)的性能 。
-
衡量预测 TDT 值
与真实 TDT 值
之间的差异 。
(其中 是基于预测目标值
计算出的一阶差分序列 。)
自适应权重  (Adaptive Weight
(Adaptive Weight  )
)
-
用于动态地平衡
和
这两个损失分量的重要性 。
-
它衡量模型学习粗粒度 TDT(即递增/递减关系)的能力 。
-
定义:
代表预测的 TDT 值
与真实值
之间符号不一致的比例 。
(其中
是符号函数,
是指示函数 。)
-
动态平衡机制:
。
-
值大: 表明模型在预测递增/递减关系方面表现不佳(粗粒度 TDT 学习不足),此时
(目标预测损失)的权重
较大,促使模型先专注于准确预测目标值 。
-
值小: 表明模型预测符号的能力较好,随着模型预测能力的提高,
逐渐减小,
(TDT 学习损失)的权重
相应增大,从而引导模型将注意力转移到学习和预测细粒度 TDT(具体的增量/减量值)上,实现对时间序列的更全面理解 。
-
通过这种方式,TDT Loss 使得 NAR 模型能够端到端地学习目标值、粗粒度 TDT 和细粒度 TDT,从而显著提高整体预测性能 。
实验
Experimental Setup
数据集
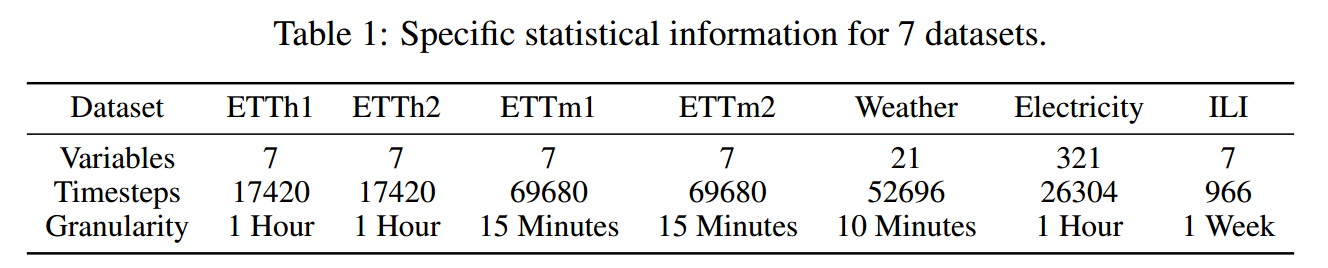
Base Models
-
基于 MLP 的模型: DLinear, NLinear
-
**基于 CNN 的模型:**MICN,TimesNet
-
基于 Transformer 的模型: MICN , TimesNet
Metric
MAE、MSE、 、
和
结果分析
Main Results
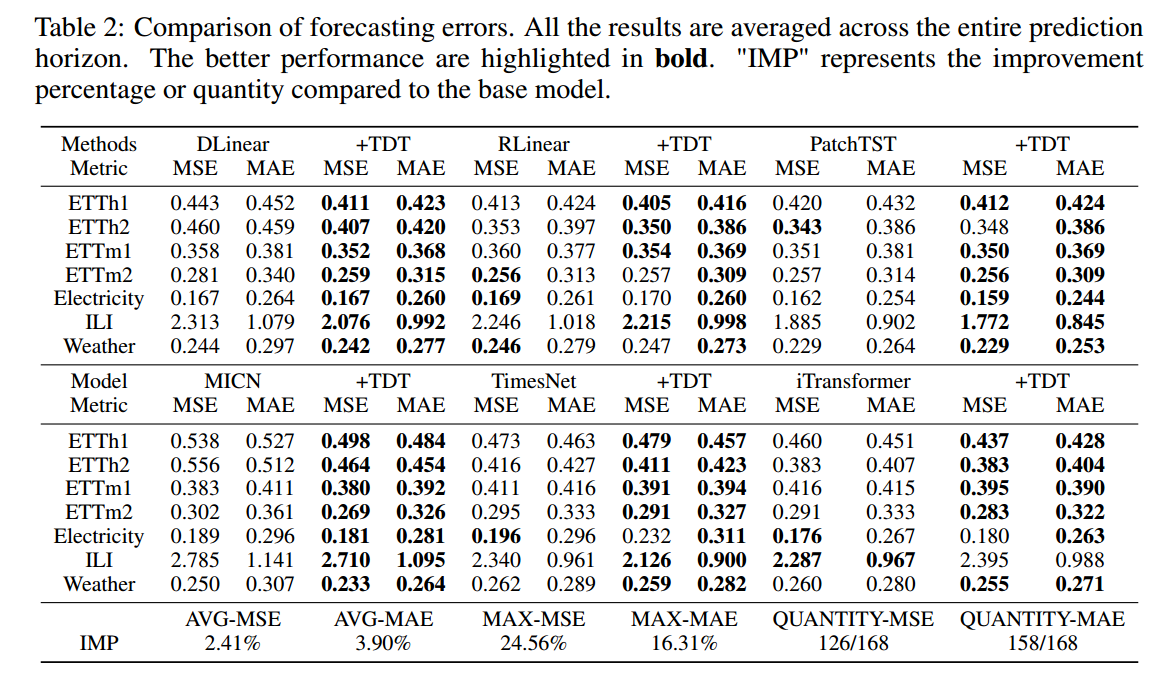
提高性能的同时,也降低了标准差,表明基础模型的预测在TDT损失下变得更加稳定。
Efficiency Analysis
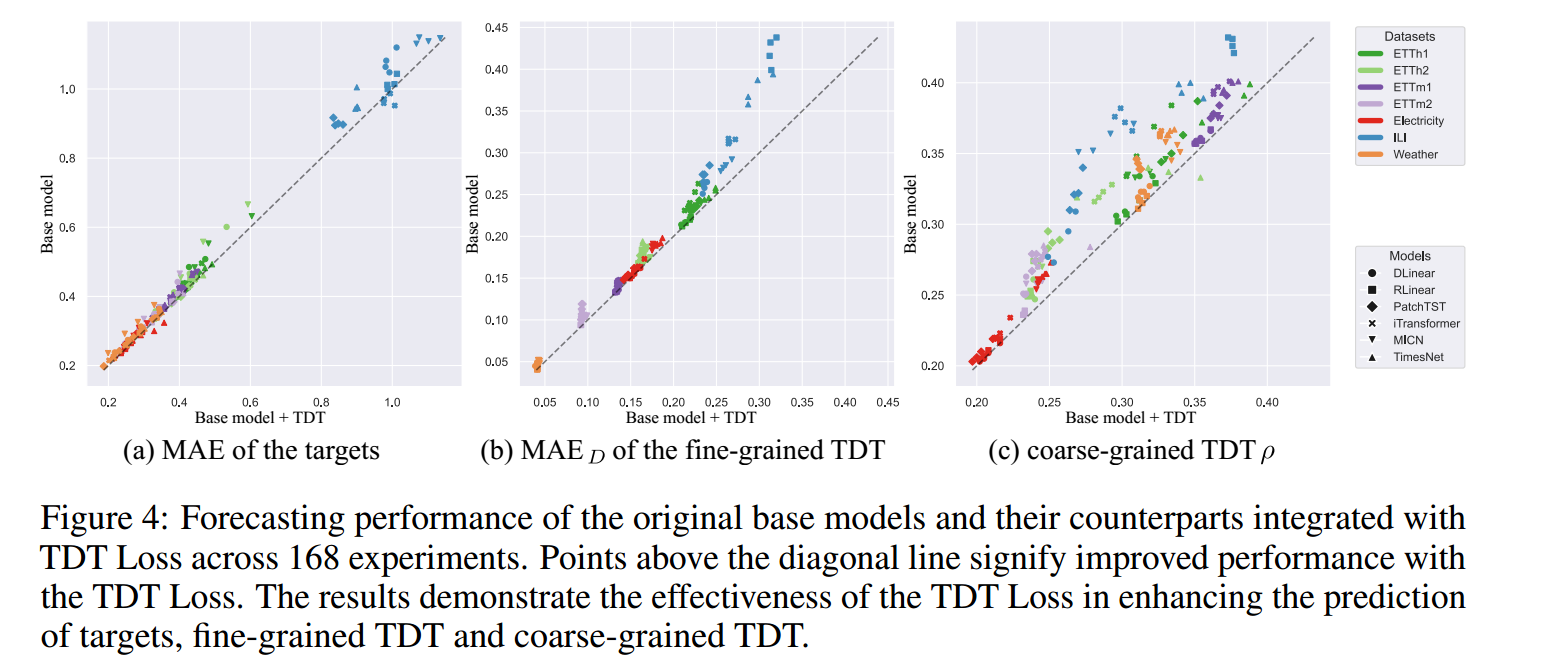
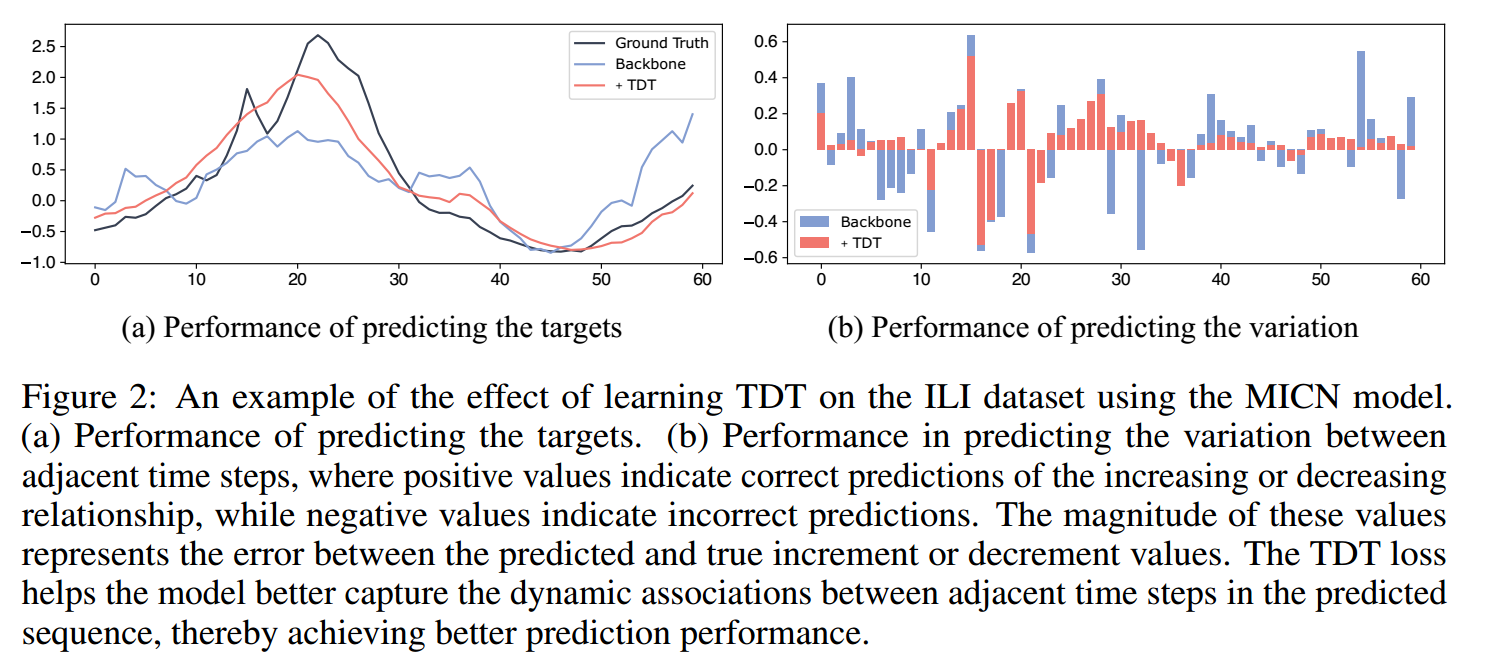
图 (a): 目标值 ( Y ) 的预测性能(MAE/MSE)。
图 (b): 细粒度 TDT(TDT 值 D)的预测性能。
图 (c): 粗粒度 TDT(TDT 符号)的预测性能。
TDT 预测能力和目标值预测能力之间存在强烈的正向关联,TDT Loss 通过优化 TDT 预测,确实达到了提升最终目标值预测效果的目的。
Ablation Study
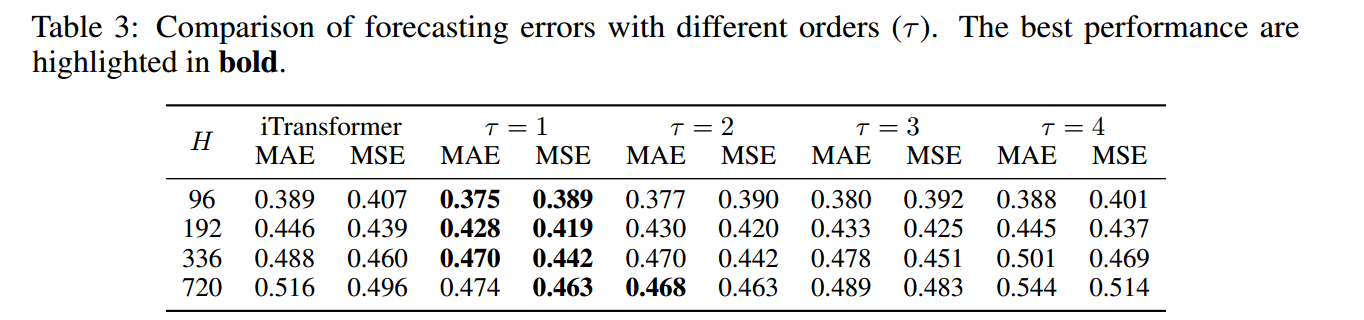
一阶差分(相邻时间步的差异)提供了足够且易于模型学习的信息。更高的阶数(如二阶、三阶)并没有带来额外信息,反而可能过度约束模型,导致性能下降。
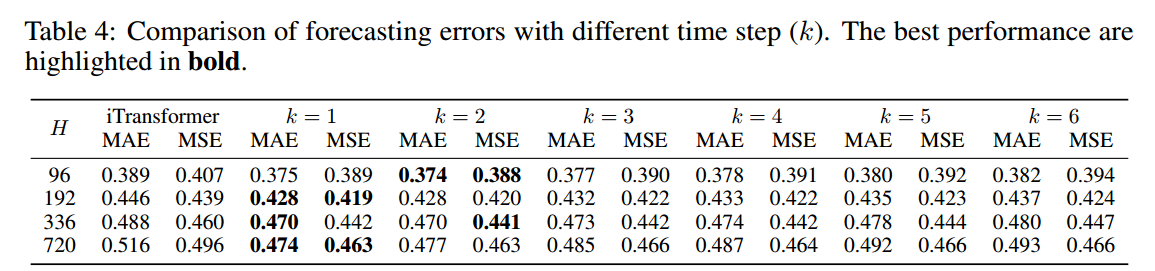
TDT 主要存在于相邻时间步 之间。较大的时间间隔(更大的 k )可能会忽略中间时间步的有价值信息,并且依赖关系相比相邻时间步更弱。
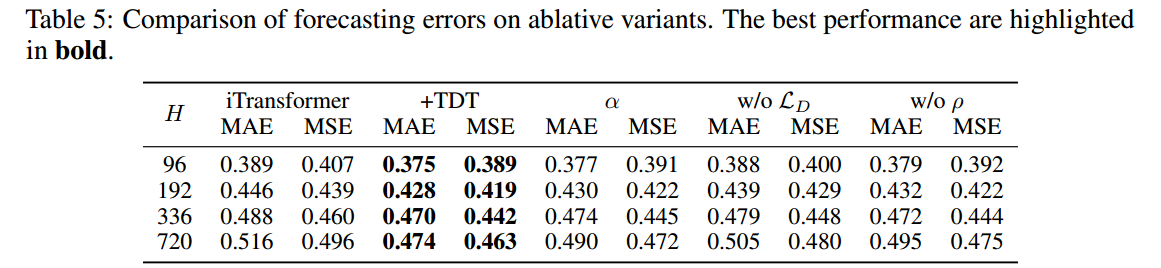
-
iTransformer +TDT: 完整 TDT Loss 方案 -
w/o LD: 排除细粒度 TDT 损失 ,只学习和粗粒度 TDT (通过
)。
-
w/o ρ: 排除自适应权重,只使用
和
,且不动态调整权重。
-
α(Adaptive learning weight α): 另一个替代的自适应学习权重。