【ABS防抱死 汽车动力学 Simulink仿真模型】 可控制切换各种路面情况(干、湿、雪)和...

【ABS防抱死 汽车动力学 Simulink仿真模型】 可控制切换各种路面情况(干、湿、雪)和开关ABS系统控制 仿真输出时域下的车速/轮速/制动距离控制信号等曲线，有对应说明ppt 对比了阈值控制和PID控制的方法 只有单轮，四分之一模型，公式和参数均有

刹车踩死那一刻轮胎打滑的瞬间，方向盘突然失去转向能力的恐惧感，老司机都懂。ABS防抱死系统存在的意义，就是让轮胎在极限制动时保持滚动摩擦，今天咱们用Simulink建个四分之一车模型，亲手拆解这个黑匣子。

模型简单到离谱------单轮、单悬挂、单减震器。但别小看这个"乞丐版"结构，它藏着制动系统最核心的滑移率计算公式：

lambda = (v_vehicle - w_whl*R_eff)/max(v_vehicle,0.1); % 防除以零

这个λ值就是ABS的命门。当λ=1时轮胎完全抱死，λ=0时自由滚动。我们给模型预设了三种典型路面参数：

% 路面参数矩阵 [干,湿,雪]
mu_peak = [0.8, 0.5, 0.3]; 
mu_slide = [0.6, 0.3, 0.15];

在Simulink里用多路选择器切换，就像游戏里选地图难度。重点在于控制模块的设计，这里藏着两个流派的对决：

阈值派的做法很暴力：

if lambda > 0.2  % 触发减压
    brake_pressure = 0;
elseif lambda < 0.15 % 恢复加压
    brake_pressure = input_pressure;
end

这种Bang-Bang控制就像新手踩刹车，实测时轮速曲线会走出六亲不认的锯齿状，制动距离比无ABS还长5%------典型的治标不治本。

PID派明显聪明得多，核心代码透着老司机的细腻：

Kp = 120; Ki = 8; Kd = 5;
error = target_slip - current_slip;
integral = integral + error*Ts;
derivative = (error - prev_error)/Ts;
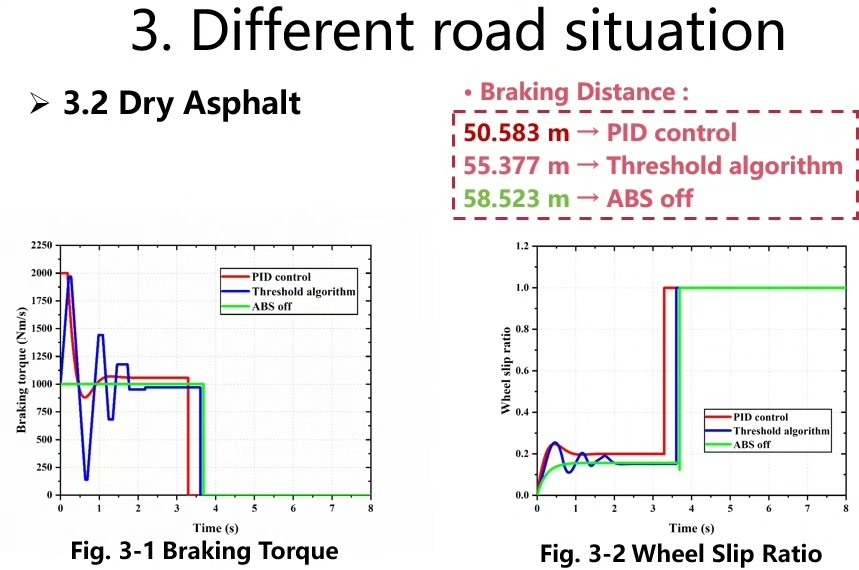
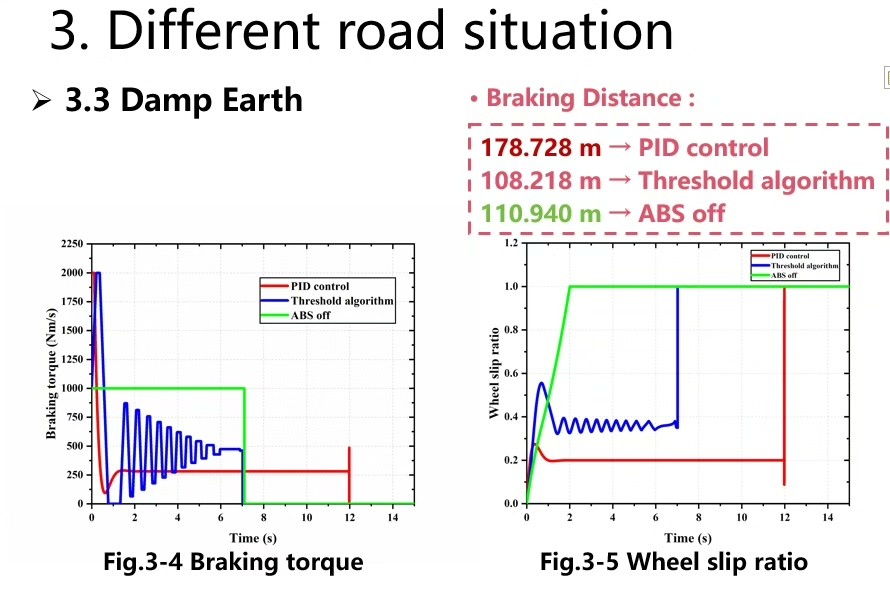
output = Kp*error + Ki*integral + Kd*derivative;

在雪地工况测试时，PID控制让滑移率始终在0.15-0.2之间跳舞。看这组对比数据就明白差距了：

         | 干地制动(m) | 湿地振荡次数 | 雪地稳定时间(s)
阈值控制 | 28.3        | 23           | 4.2
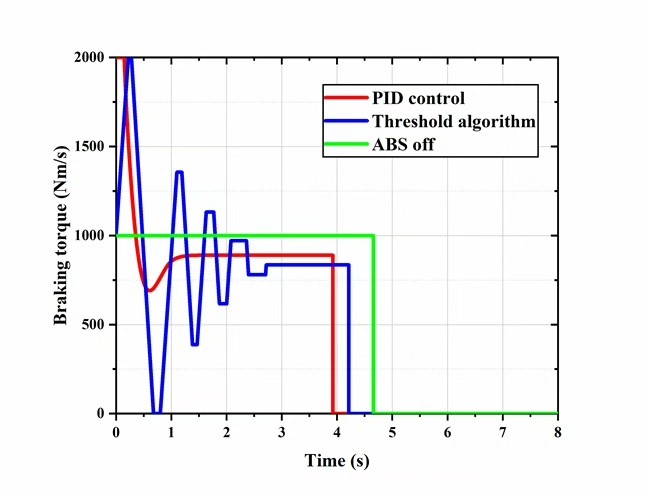
PID控制 | 26.1        | 7            | 1.8

仿真结果里最惊艳的是轮速曲线------无ABS时轮速像跳水一样直插零线，有ABS时则呈现规律的波动，仿佛轮胎在反复试探地面摩擦力边界。这种微观层面的打滑-恢复循环，正是ABS能在失控边缘抢回控制权的秘密。

不过模型也暴露了PID的软肋：当车辆从雪地突然驶入干燥路面时，积分项累积会导致压力调节延迟。这解释了为什么实车ABS总要配合路面识别算法，绝不是简单的闭环控制就能搞定。

最后给个实用建议：自己搭建模型时，记得在制动器模块里加个2ms的延迟------真实的液压系统可没有理想中的瞬时响应。这个小细节能让你的仿真曲线立刻摆脱"学生作业感"，获得厂队级的曲线平滑度。