第五届机电一体化、自动化与智能控制国际学术会议（MAIC 2025）

重要信息

官网： https://ais.cn/u/iInuie

**时间：**2025年12月19-21日

**地点：**广东·湛江·岭南师范学院（寸金校区）

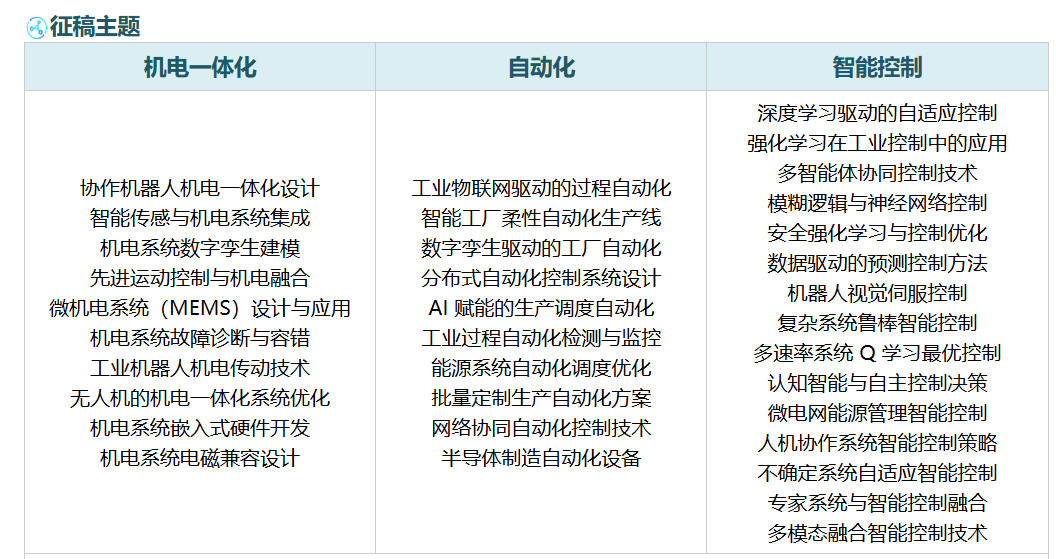
征稿主题

一、机电一体化的核心技术体系

1.1 机电一体化系统的架构组成

机电一体化系统融合机械、电子、控制等多学科技术，其核心架构可划分为以下模块：

系统模块	核心技术	典型组件
机械本体	精密机械设计、机构优化	伺服电机、传动机构、执行部件
传感检测	多传感器融合、信号处理	编码器、力传感器、视觉传感器
控制单元	嵌入式系统、PLC/DCS	单片机、FPGA、工业控制器
驱动系统	伺服驱动、变频控制	伺服驱动器、步进电机驱动器

1.2 机电一体化的关键技术特征

机电一体化系统具备集成化 、智能化 、柔性化等特征，其中：

• 集成化体现为机械结构与电控系统的深度融合
• 智能化依赖传感器感知与智能算法决策
• 柔性化通过模块化设计实现多任务适配

二、自动化控制技术的实践应用

2.1 PID 控制算法的实现与优化

PID 控制是工业自动化的核心算法，以下是基于 Python 的 PID 控制器实现示例：

python

运行

class PIDController:
    def __init__(self, kp, ki, kd, setpoint=0):
        self.kp = kp  # 比例系数
        self.ki = ki  # 积分系数
        self.kd = kd  # 微分系数
        self.setpoint = setpoint  # 目标值
        self.error_sum = 0  # 误差积分
        self.last_error = 0  # 上一次误差

    def compute(self, process_value, dt):
        # 计算当前误差
        error = self.setpoint - process_value
        # 比例项
        p_term = self.kp * error
        # 积分项
        self.error_sum += error * dt
        i_term = self.ki * self.error_sum
        # 微分项
        d_term = self.kd * (error - self.last_error) / dt
        self.last_error = error
        # 计算输出
        output = p_term + i_term + d_term
        return output

# PID控制示例（控制温度）
pid = PIDController(kp=2.0, ki=0.5, kd=0.1, setpoint=50.0)
current_temp = 25.0  # 初始温度
dt = 0.1  # 采样时间

for _ in range(100):
    control_signal = pid.compute(current_temp, dt)
    current_temp += control_signal * 0.5  # 温度响应
    print(f"当前温度：{current_temp:.2f}°C，控制输出：{control_signal:.2f}")

2.2 运动控制系统的轨迹规划

运动控制中的轨迹规划直接影响系统精度与稳定性，以下是关节空间轨迹规划示例：

python

运行

import numpy as np

def cubic_trajectory(start, end, t_total, t):
    """
    三次多项式轨迹规划
    :param start: 起始位置
    :param end: 终止位置
    :param t_total: 总运动时间
    :param t: 当前时间
    :return: 当前位置、速度
    """
    # 三次多项式系数计算
    a0 = start
    a1 = 0
    a2 = 3 * (end - start) / (t_total ** 2)
    a3 = -2 * (end - start) / (t_total ** 3)
    
    # 位置与速度计算
    position = a0 + a1 * t + a2 * t**2 + a3 * t**3
    velocity = a1 + 2 * a2 * t + 3 * a3 * t**2
    return position, velocity

# 轨迹生成示例（关节从0°到90°运动）
t_total = 2.0  # 总运动时间2秒
time_points = np.linspace(0, t_total, 100)
trajectory = []

for t in time_points:
    pos, vel = cubic_trajectory(0, 90, t_total, t)
    trajectory.append((t, pos, vel))

# 输出轨迹关键点
for i in range(0, 100, 20):
    t, pos, vel = trajectory[i]
    print(f"时间：{t:.2f}s，位置：{pos:.2f}°，速度：{vel:.2f}°/s")

三、智能控制技术的创新发展

3.1 模糊控制在非线性系统中的应用

模糊控制适用于难以建立精确数学模型的非线性系统，以下是液位模糊控制示例：

python

运行

class FuzzyController:
    def __init__(self):
        # 定义模糊集合（误差：负大、负小、零、正小、正大）
        self.error_mf = {
            'NB': lambda x: max(0, (x + 6) / 2) if x < -4 else (max(0, (-x - 2) / 2) if x < -2 else 0),
            'NS': lambda x: max(0, (x + 4) / 2) if x < -2 else (max(0, (-x) / 2) if x < 0 else 0),
            'Z': lambda x: max(0, (x + 2) / 2) if x < 0 else (max(0, (2 - x) / 2) if x < 2 else 0),
            'PS': lambda x: max(0, x / 2) if x < 2 else (max(0, (4 - x) / 2) if x < 4 else 0),
            'PB': lambda x: max(0, (x - 2) / 2) if x < 4 else (max(0, (x - 4) / 2) if x < 6 else 0)
        }
        # 控制规则表
        self.rules = {
            'NB': 'PB', 'NS': 'PS', 'Z': 'Z', 'PS': 'NS', 'PB': 'NB'
        }

    def infer(self, error):
        # 计算误差隶属度
        mf_values = {key: func(error) for key, func in self.error_mf.items()}
        # 非零隶属度的规则
        active_rules = {k: v for k, v in mf_values.items() if v > 0}
        # 加权平均解模糊
        output = 0
        total_weight = 0
        for error_level, weight in active_rules.items():
            control_level = self.rules[error_level]
            # 控制量量化（PB=3, PS=1, Z=0, NS=-1, NB=-3）
            control_value = {'PB':3, 'PS':1, 'Z':0, 'NS':-1, 'NB':-3}[control_level]
            output += control_value * weight
            total_weight += weight
        return output / total_weight if total_weight > 0 else 0

# 模糊控制示例（水箱液位控制）
fuzzy_ctrl = FuzzyController()
current_level = 0  # 初始液位
set_level = 5  # 目标液位

for _ in range(50):
    error = set_level - current_level
    control = fuzzy_ctrl.infer(error)
    current_level += control * 0.3  # 液位响应
    print(f"液位误差：{error:.2f}，控制输出：{control:.2f}，当前液位：{current_level:.2f}")

3.2 强化学习在自适应控制中的应用

强化学习通过与环境交互实现控制策略优化，以下是倒立摆控制示例：

python

运行

import numpy as np

class QLearningController:
    def __init__(self, state_bins, action_count, alpha=0.1, gamma=0.9, epsilon=0.1):
        self.state_bins = state_bins  # 状态离散化区间
        self.action_count = action_count  # 动作数量
        self.q_table = np.zeros(state_bins + (action_count,))  # Q表初始化
        self.alpha = alpha  # 学习率
        self.gamma = gamma  # 折扣因子
        self.epsilon = epsilon  # 探索率

    def discretize_state(self, state):
        # 状态离散化（角度、角速度）
        angle_bin = np.digitize(state[0], bins=np.linspace(-np.pi, np.pi, self.state_bins[0]-1))
        vel_bin = np.digitize(state[1], bins=np.linspace(-8, 8, self.state_bins[1]-1))
        return (angle_bin, vel_bin)

    def choose_action(self, state):
        # ε-贪心策略选择动作
        if np.random.uniform(0, 1) < self.epsilon:
            return np.random.choice(self.action_count)
        else:
            return np.argmax(self.q_table[self.discretize_state(state)])

    def learn(self, state, action, reward, next_state, done):
        # Q值更新
        state_idx = self.discretize_state(state)
        next_state_idx = self.discretize_state(next_state)
        old_value = self.q_table[state_idx + (action,)]
        next_max = np.max(self.q_table[next_state_idx]) if not done else 0
        new_value = old_value + self.alpha * (reward + self.gamma * next_max - old_value)
        self.q_table[state_idx + (action,)] = new_value

# 简化倒立摆环境
def pendulum_step(state, action):
    angle, angle_vel = state
    # 动作：-1（左推）、0（不动）、1（右推）
    torque = (action - 1) * 0.5
    angle_vel += (3 * np.cos(angle) + torque) * 0.05
    angle += angle_vel * 0.05
    angle_vel *= 0.99  # 阻尼
    # 奖励计算（角度接近0奖励高）
    reward = np.cos(angle)
    done = abs(angle) > np.pi/2
    return (angle, angle_vel), reward, done

# 训练过程
q_ctrl = QLearningController(state_bins=(10, 10), action_count=3)
episodes = 1000

for episode in range(episodes):
    state = (np.random.uniform(-np.pi/4, np.pi/4), 0)
    total_reward = 0
    for _ in range(200):
        action = q_ctrl.choose_action(state)
        next_state, reward, done = pendulum_step(state, action)
        q_ctrl.learn(state, action, reward, next_state, done)
        state = next_state
        total_reward += reward
        if done:
            break
    if episode % 100 == 0:
        print(f"Episode {episode}: 总奖励 = {total_reward:.2f}")

四、机电一体化系统的集成与优化

4.1 嵌入式控制系统的设计

嵌入式系统是机电一体化的核心控制单元，其设计流程包括：

1. 需求分析：确定控制功能、性能指标、接口需求
2. 硬件选型：MCU/MPU、传感器、通信模块选型
3. 软件设计：实时操作系统（RTOS）移植、驱动开发
4. 系统调试：硬件测试、软件仿真、联合调试

4.2 多传感器融合技术

多传感器融合提升系统感知精度与可靠性，常见融合算法对比：

融合算法	原理	优势	适用场景
卡尔曼滤波	状态估计与误差协方差更新	实时性好、精度高	线性系统
粒子滤波	蒙特卡洛采样与权重更新	适用于非线性系统	复杂环境感知
D-S 证据理论	证据组合与信任函数	处理不确定性信息	多源异构数据融合

五、国际交流与合作机会

作为国际学术会议，将吸引全球范围内的专家学者参与。无论是发表研究成果、聆听特邀报告，还是在圆桌论坛中与行业大咖交流，都能拓宽国际视野，甚至找到潜在的合作伙伴。对于高校师生来说，这也是展示研究、积累学术人脉的好机会。