摘要
使用扩散概率模型(一类受非平衡热力学启发的潜变量模型)展示了高质量的图像合成结果。作者最佳的结果是通过在加权变分界上进行训练获得的,该界是根据扩散概率模型与带朗之万动力学的去噪分数匹配之间的新型联系设计的,并且作者的模型自然地支持一种渐进式有损解压方案,这可以被解释为自回归解码的推广。在无条件 CIFAR10 数据集上,作者获得了 9.46 的 Inception 分数和 3.17 的最先进 FID 分数。在 256x256 的 LSUN 数据集上,作者获得了与 ProgressiveGAN 相似的样本质量。我们的实现可在 https://github.com/hojonathanho/diffusion 获取。
核心思想解析
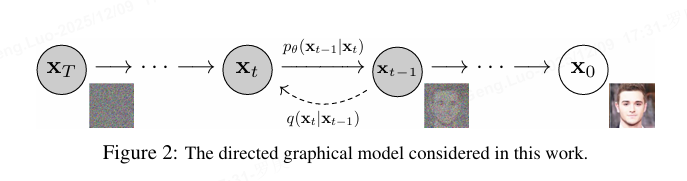
Denoising Diffusion Probabilistic Models (DDPM) 是一种基于扩散过程的生成模型,通过逐步添加和去除噪声实现数据生成。其核心分为前向扩散(加噪)和反向扩散(去噪)两个过程,最终学习从噪声中重构数据。
重参数化

前向扩散过程
前向过程将数据逐渐转化为高斯噪声,每一步根据预设的噪声调度参数 βt\beta_tβt 添加噪声。给定数据 x0x_0x0,第 ttt 步的加噪结果 xtx_txt 服从以下分布:
q(xt∣xt−1)=N(xt;1−βtxt−1,βtI) q(x_t|x_{t-1}) = \mathcal{N}(x_t; \sqrt{1-\beta_t}x_{t-1}, \beta_t\mathbf{I}) q(xt∣xt−1)=N(xt;1−βt xt−1,βtI)
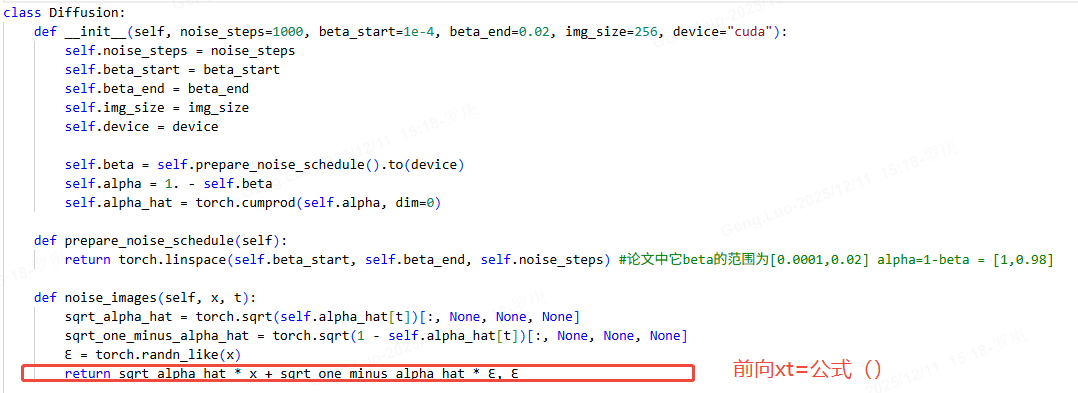
通过重参数化技巧,可直接从 x0x_0x0 计算任意 ttt 步的噪声数据:
xt=αˉtx0+1−αˉtϵ x_t = \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon xt=αˉt x0+1−αˉt ϵ
其中 αt=1−βt\alpha_t = 1-\beta_tαt=1−βt,αˉt=∏s=1tαs\bar{\alpha}t = \prod{s=1}^t \alpha_sαˉt=∏s=1tαs,ϵ∼N(0,I)\epsilon \sim \mathcal{N}(0, \mathbf{I})ϵ∼N(0,I)。


反向扩散过程
反向过程通过神经网络学习逐步去噪。模型预测噪声 ϵθ\epsilon_\thetaϵθ 以重构数据,目标是最小化以下损失函数:
L=Et,x0,ϵ[∥ϵ−ϵθ(xt,t)∥2] \mathcal{L} = \mathbb{E}{t,x_0,\epsilon}\left[\|\epsilon - \epsilon\theta(x_t,t)\|^2\right] L=Et,x0,ϵ[∥ϵ−ϵθ(xt,t)∥2]
去噪每一步的均值和方差通过以下公式计算:
pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t)) p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t,t), \Sigma_\theta(x_t,t)) pθ(xt−1∣xt)=N(xt−1;μθ(xt,t),Σθ(xt,t))
其中 μθ\mu_\thetaμθ 通常由预测噪声 ϵθ\epsilon_\thetaϵθ 推导得出。



训练与生成步骤
训练阶段:
- 从数据集中采样 x0x_0x0,随机选择时间步 ttt。
- 生成噪声 ϵ\epsilonϵ 并计算 xtx_txt。
- 训练神经网络 ϵθ\epsilon_\thetaϵθ 预测噪声,优化均方误差损失。
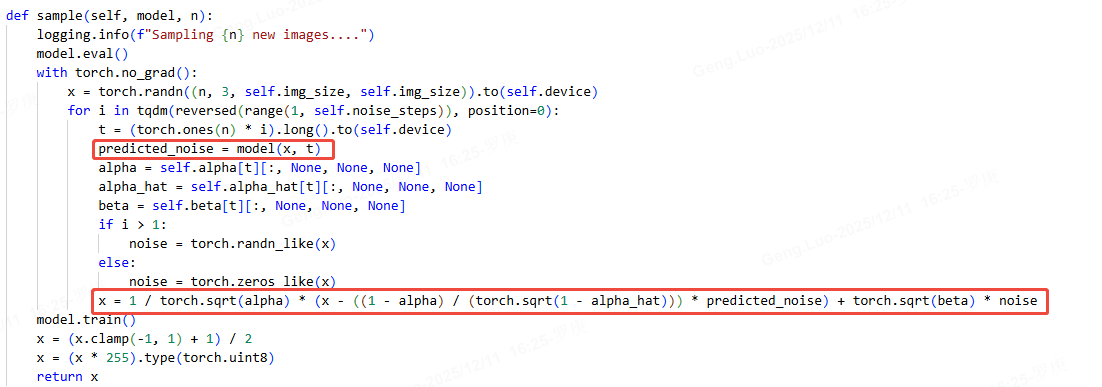
生成阶段:
- 从高斯噪声 xTx_TxT 开始,逐步去噪至 x0x_0x0。
- 每一步使用 ϵθ\epsilon_\thetaϵθ 预测噪声,并通过采样得到 xt−1x_{t-1}xt−1。
关键改进与扩展
- 噪声调度 :线性或余弦调度的 βt\beta_tβt 影响训练稳定性和生成质量。
- 加速采样:DDIM(Denoising Diffusion Implicit Models)通过非马尔可夫链加速生成。
- 条件生成:通过分类器引导或嵌入条件信息实现可控生成。
代码实现要点
python
# 噪声预测网络结构(U-Net为例)
class UNet(nn.Module):
def __init__(self):
super().__init__()
self.time_embed = nn.Sequential(
nn.Linear(embed_dim, time_emb_dim),
nn.SiLU(),
nn.Linear(time_emb_dim, time_emb_dim)
)
self.down_blocks = nn.ModuleList([DownsampleBlock(...) for _ in range(num_layers)])
self.up_blocks = nn.ModuleList([UpsampleBlock(...) for _ in range(num_layers)])
# 训练循环核心步骤
def train_step(x0, t):
noise = torch.randn_like(x0)
xt = sqrt_alphas_cumprod[t] * x0 + sqrt_one_minus_alphas_cumprod[t] * noise
predicted_noise = model(xt, t)
loss = F.mse_loss(predicted_noise, noise)
return loss数学推导补充
反向过程的真实后验分布 q(xt−1∣xt,x0)q(x_{t-1}|x_t,x_0)q(xt−1∣xt,x0) 可解析计算为:
q(xt−1∣xt,x0)=N(xt−1;μ~t(xt,x0),β~tI) q(x_{t-1}|x_t,x_0) = \mathcal{N}(x_{t-1}; \tilde{\mu}_t(x_t,x_0), \tilde{\beta}_t\mathbf{I}) q(xt−1∣xt,x0)=N(xt−1;μ~t(xt,x0),β~tI)
其中:
μ~t=αˉt−1βt1−αˉtx0+αt(1−αˉt−1)1−αˉtxt \tilde{\mu}t = \frac{\sqrt{\bar{\alpha}{t-1}}\beta_t}{1-\bar{\alpha}t}x_0 + \frac{\sqrt{\alpha_t}(1-\bar{\alpha}{t-1})}{1-\bar{\alpha}_t}x_t μ~t=1−αˉtαˉt−1 βtx0+1−αˉtαt (1−αˉt−1)xt
β~t=1−αˉt−11−αˉtβt \tilde{\beta}t = \frac{1-\bar{\alpha}{t-1}}{1-\bar{\alpha}_t}\beta_t β~t=1−αˉt1−αˉt−1βt
模型通过拟合 μ~t\tilde{\mu}_tμ~t 实现去噪。