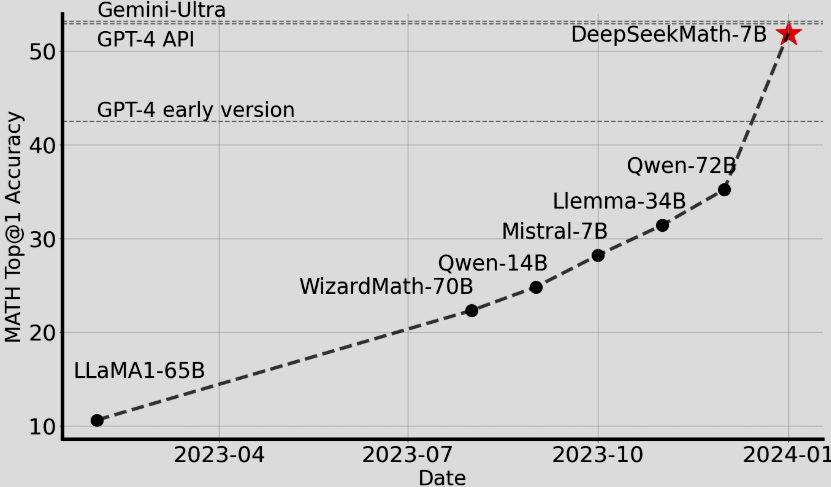
GRPO (Generative Reward-Paired Optimization) 是由 DeepSeek (深度求索) 团队在发布 DeepSeek-R1 (DeepSeek-Math) 相关论文时提出的一种新型强化学习(RL)算法。
它的核心目标是:在不使用"评论家模型"(Critic Model)的情况下,实现高效的强化学习微调,从而大幅降低训练时的显存占用和计算成本。
以下是 GRPO 原理的详细深度解析:
1. 背景:为什么需要 GRPO?(PPO 的痛点)
在传统的 RLHF(基于人类反馈的强化学习)中,主流算法是 PPO (Proximal Policy Optimization)。虽然 PPO 效果好,但它极其"昂贵"。
一个标准的 PPO 训练过程通常需要加载 4 个模型:
- Policy Model (Actor): 正在训练的模型(如 7B 参数)。
- Reference Model: 冻结的原始模型,用于计算 KL 散度,防止模型跑偏(7B 参数)。
- Reward Model: 奖励模型,用于给输出打分(通常也是 7B 或更大)。
- Value Model (Critic): 价值模型,用于估计当前状态的预期收益,指导 Actor 更新(通常与 Policy 同规模,7B)。
痛点:对于一个 7B 的模型,PPO 可能需要占用 4 倍的显存。对于 70B 的模型,这几乎是不可接受的资源消耗。此外,训练 Value Model (Critic) 本身就很难,且容易不稳定。
2. GRPO 的核心思想:以"组"为单位的相对优势
GRPO 抛弃了 Value Model (Critic)。
它不再需要一个额外的神经网络来告诉 Policy "你这一步做得好不好"。相反,它利用 "组内比较" (Group Relative Comparison) 来计算优势(Advantage)。
核心流程 (Step-by-Step)
假设我们有一个数学问题 q q q(Prompt)。
-
组采样 (Group Sampling) :
Policy Model 对同一个问题 q q q,生成一组(Group)共 G G G 个不同的回答 { o 1 , o 2 , . . . , o G } \{o_1, o_2, ..., o_G\} {o1,o2,...,oG}。
- 例如: G = 64 G=64 G=64,即生成 64 个不同的解题过程。
-
奖励计算 (Reward Calculation) :
使用奖励模型(或规则检查器,如数学题答案是否正确)对这 G G G 个回答分别打分,得到奖励值 { r 1 , r 2 , . . . , r G } \{r_1, r_2, ..., r_G\} {r1,r2,...,rG}。
-
优势估计 (Advantage Estimation) ------ 魔法所在 :
GRPO 不依赖 Critic 模型预测基准线(Baseline),而是直接使用这就 G G G 个回答的平均分作为基准线。
第 i i i 个回答的优势 A i A_i Ai 计算公式为:
A i = r i − mean ( { r 1 . . . r G } ) std ( { r 1 . . . r G } ) A_i = \frac{r_i - \text{mean}(\{r_1...r_G\})}{\text{std}(\{r_1...r_G\})} Ai=std({r1...rG})ri−mean({r1...rG})- 直观理解 :如果你的得分 r i r_i ri 高于这组回答的平均分,你的优势 A i A_i Ai 就是正的(受到鼓励);如果低于平均分,优势就是负的(受到惩罚)。
- 通过除以标准差,实现了归一化,使训练更稳定。
-
策略更新 (Policy Optimization) :
利用计算出的优势 A i A_i Ai,通过 PPO 的目标函数形式来更新 Policy Model 的参数。最大化那些 A i > 0 A_i > 0 Ai>0 的样本的生成概率,最小化 A i < 0 A_i < 0 Ai<0 的样本。
3. GRPO vs PPO 架构对比图
为了更直观地理解,我们可以对比两者的架构:
🏛️ 传统 PPO 架构
需要维护一个庞大的 Critic 网络来预测 Value。
Prompt Policy Model Response RewardModel Value Model Reward ValuePred 计算 Advantage: R - V 更新 Actor 和 Critic
🚀 GRPO 架构 (DeepSeek)
去掉了 Critic,通过多次采样自己和自己比。
Prompt Policy Model Response 1 Response 2 Response ...n 奖励函数/模型 得分列表: r1, r2, ...rn 计算平均分 Mean 计算相对优势: (ri - Mean)/Std 更新 Actor
4. GRPO 的数学原理 (简化版)
GRPO 的目标函数大致如下:
J G R P O ( θ ) = E q ∼ P ( Q ) , { o i } i = 1 G ∼ π θ o l d ( q ) [ 1 G ∑ i = 1 G ( min ( π θ ( o i ∣ q ) π θ o l d ( o i ∣ q ) A i , clip ( . . . ) A i ) − β D K L ) ] J_{GRPO}(\theta) = \mathbb{E}{q \sim P(Q), \{o_i\}{i=1}^G \sim \pi_{\theta_{old}}(q)} \left[ \frac{1}{G} \sum_{i=1}^G \left( \min \left( \frac{\pi_\theta(o_i|q)}{\pi_{\theta_{old}}(o_i|q)} A_i, \text{clip}(...) A_i \right) - \beta D_{KL} \right) \right] JGRPO(θ)=Eq∼P(Q),{oi}i=1G∼πθold(q)[G1i=1∑G(min(πθold(oi∣q)πθ(oi∣q)Ai,clip(...)Ai)−βDKL)]
看起来很复杂,其实包含三个关键部分:
- 重要性采样 (Importance Sampling) : π θ π o l d \frac{\pi_\theta}{\pi_{old}} πoldπθ,衡量新策略和旧策略的比例,确保更新步长不要太大(PPO 机制)。
- 相对优势 A i A_i Ai: 如前所述,通过组内归一化计算得出。
- KL 散度惩罚 ( D K L D_{KL} DKL): 防止模型为了刷高分而彻底改变输出分布,导致语言能力退化(例如防止模型输出乱码但碰巧包含了正确答案)。
5. GRPO 的核心优势
1. 显存占用大幅降低 📉
这是 GRPO 最大的卖点。因为它不需要 Value Model (Critic)。在微调超大模型(如 DeepSeek-V3, Llama-3-70B)时,这节省了数十 GB 的显存,使得在资源受限的情况下进行 RL 微调成为可能。
2. 无需训练 Critic,稳定性提升 ⚖️
在 PPO 中,Critic 模型的训练非常困难。如果 Critic 估值不准,Actor 就会学歪。GRPO 直接用采样的真实结果的平均值作为基准,消除了 Critic 估值偏差带来的不稳定性。
3. 特别适合推理/数学/代码任务 🧮
对于有明确答案的任务(Math, Code),GRPO 效果极佳。
- 模型生成 64 个解题路径。
- 其中 10 个做对了,54 个做错了。
- GRPO 会自动将这 10 个正确路径标记为正样本,54 个错误路径标记为负样本。
- 模型通过自我博弈,学会了哪种推理步骤更有可能导致正确结果。这正是 DeepSeek-R1 能够涌现出强大 CoT(思维链)能力的原因。
6. GRPO 的局限性
虽然 GRPO 很强,但也不是万能的:
- 采样开销大 : 每个 Prompt 需要推理 G G G 次(例如 64 次)。这意味着训练时的推理计算量(Inference Cost) 变大了。你需要强大的推理后端(如 vLLM)来支撑训练循环。
- 依赖 Reward 准确性: GRPO 非常依赖 Reward Function。在数学/代码领域,Reward 是客观的(对/错)。但在创意写作领域,如果没有一个好的 Reward Model,组内比较可能意义不大(大家都写得一般,平均分也一般,很难区分优劣)。
总结
GRPO 是强化学习微调的一种"减法"艺术。
它去掉了复杂的价值网络(Critic),用"暴力"的多重采样(Group Sampling)和统计学上的相对优势(Relative Advantage)取而代之。
- PPO: 像是一个学生每做一道题,旁边都有一个老师(Critic)告诉他这题大概能得几分,即使没出成绩也能指导。
- GRPO: 像是一个学生把一道题做了 10 遍,交卷后发现 3 遍是对的,7 遍是错的。他通过对比这 10 遍的差异,自己总结出解题规律,不需要老师时刻在旁指导。
论文
- 论文标题 :
DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models - ArXiv 链接 : 点击跳转 (arXiv:2402.03300)
- PDF 直接下载 : 点击下载 PDF
- 发布时间 : 2024年2月