论文笔记（一百零九）Discovering state-of-the-art reinforcement learning algorithms

Discovering state-of-the-art reinforcement learning algorithms

文章概括
ABSTRACT
[Discovery method](#Discovery method)
- [Agent network](#Agent network)
- Meta-network（元网络）
- [Agent optimization](#Agent optimization)
- Meta-optimization（元优化）
[Empirical result（实证结果）](#Empirical result（实证结果）)
- Atari
- Generalization（泛化性）
- [Complex and diverse environments（复杂且多样的环境）](#Complex and diverse environments（复杂且多样的环境）)
- [Efficiency and scalability（效率与可扩展性）](#Efficiency and scalability（效率与可扩展性）)
- [Effect of discovering new predictions（发现新预测的影响）](#Effect of discovering new predictions（发现新预测的影响）)
Analysis（分析）
- [Qualitative analysis（定性分析）](#Qualitative analysis（定性分析）)
- [Information analysis（信息分析）](#Information analysis（信息分析）)
- [Emergence of bootstrapping（自举机制的涌现）](#Emergence of bootstrapping（自举机制的涌现）)
[Previous work（相关工作）](#Previous work（相关工作）)
Conclusion（结论）
[Online content（在线内容）](#Online content（在线内容）)
Methods（方法）
- Meta-network（元网络）
- [Meta-optimization stabilization（元优化的稳定化）](#Meta-optimization stabilization（元优化的稳定化）)
- [Implementation details（实现细节）](#Implementation details（实现细节）)
- [Hyperparameters and evaluation（超参数与评估）](#Hyperparameters and evaluation（超参数与评估）)
- [Analysis details（分析细节）](#Analysis details（分析细节）)
- [Data availability（数据可用性）](#Data availability（数据可用性）)
- [Code availability（代码可用性）](#Code availability（代码可用性）)
Acknowledgements（致谢）
[Author contributions（作者贡献）](#Author contributions（作者贡献）)
[Competing interests（利益冲突）](#Competing interests（利益冲突）)
[Additional information（附加信息）](#Additional information（附加信息）)

文章概括

引用：

bash 复制代码

@article{oh2025discovering,
  title={Discovering state-of-the-art reinforcement learning algorithms},
  author={Oh, Junhyuk and Farquhar, Greg and Kemaev, Iurii and Calian, Dan A and Hessel, Matteo and Zintgraf, Luisa and Singh, Satinder and van Hasselt, Hado and Silver, David},
  journal={Nature},
  pages={1--2},
  year={2025},
  publisher={Nature Publishing Group UK London}
}

markup 复制代码

Oh, J., Farquhar, G., Kemaev, I., Calian, D.A., Hessel, M., Zintgraf, L., Singh, S., van Hasselt, H. and Silver, D., 2025. Discovering state-of-the-art reinforcement learning algorithms. Nature, pp.1-2.

主页：
原文：
代码、数据和视频：

系列文章：

请在《《《文章》》》专栏中查找

宇宙声明！

引用解析部分属于自我理解补充，如有错误可以评论讨论然后改正！

ABSTRACT

人类以及其他动物使用强大的强化学习（reinforcement learning, RL）机制，而这些机制是进化在许多代的反复试错过程中发现出来的。相比之下，人工智能体通常使用人类手工设计的学习规则来学习。尽管这一方向已经被关注了几十年，但要让系统自主发现强大的RL算法这一目标仍然难以实现（1--6）。在这里，我们展示：机器可以发现一种最先进水平的RL规则，并且其表现优于人工设计的规则。这一结果是通过元学习（meta-learning）实现的：从一个智能体群体在大量复杂环境中累积的经验中进行学习。具体而言，我们的方法会发现一种RL规则，用它来更新智能体的策略（policy）和预测（predictions）。在我们的大规模实验中，所发现的规则在成熟且广泛使用的Atari基准上超过了所有已有规则，并且在一些更具挑战、且在"发现阶段"未曾见过的基准上，也优于多种最先进的RL算法。我们的发现表明：实现高级人工智能所需要的RL算法，或许很快就能从智能体的经验中被自动发现出来，而不必再依赖人工手工设计。

你可以把传统 RL 算法（PPO、Q-learning、TD、各种辅助任务）理解成：

人类写好一套"学习规则"（update rule）：

智能体每一步要预测什么？这些预测的**目标(target)**怎么定义？损失怎么写？怎么更新参数？

这篇论文做的事情是：不让人类写规则 ，而是让系统自己在很多环境里试错，自动找出一套能学得更快、更通用的 RL 更新规则 。他们把最终发现的规则叫 DiscoRL。

人工智能的首要目标，是设计能够像人类一样，在复杂环境中进行预测并采取行动以实现目标的智能体。许多最成功的智能体都基于强化学习（reinforcement learning, RL），在这种范式中，智能体通过与环境交互来学习。数十年的研究不断催生出更加高效的RL算法，并在人工智能领域取得了众多里程碑式成果，其中包括掌握围棋⁷、国际象棋⁸、《星际争霸》⁹和《我的世界》¹⁰等复杂对抗性游戏，发明新的数学工具¹¹，以及对复杂物理系统的控制¹²。

与人类不同，人类的学习机制是通过生物进化自然形成的，而RL算法通常是人工手工设计的。这种设计过程通常缓慢而费力，并且受限于人类知识和直觉的局限。尽管已有多项研究尝试自动发现学习算法¹--⁶，但尚无方法在效率和通用性上足以取代人工设计的RL系统。

在本文中，我们提出了一种自主的方法，仅通过多代智能体在各种环境中的交互经验来发现RL规则（图1a）。所发现的RL规则在多种具有挑战性的RL基准上达到了当前最先进的性能水平。我们的方法在两个方面显著区别于以往工作。首先，以往方法通常只在狭窄的RL规则空间中搜索（例如超参数¹³,¹⁴或策略损失¹,⁶），而我们的方法允许智能体探索一个表达能力更强、更广泛的RL规则空间。其次，以往工作主要在简单环境（如网格世界³,¹⁵）中进行元学习，而我们的方法在规模更大、更加复杂且多样化的环境中进行元学习。

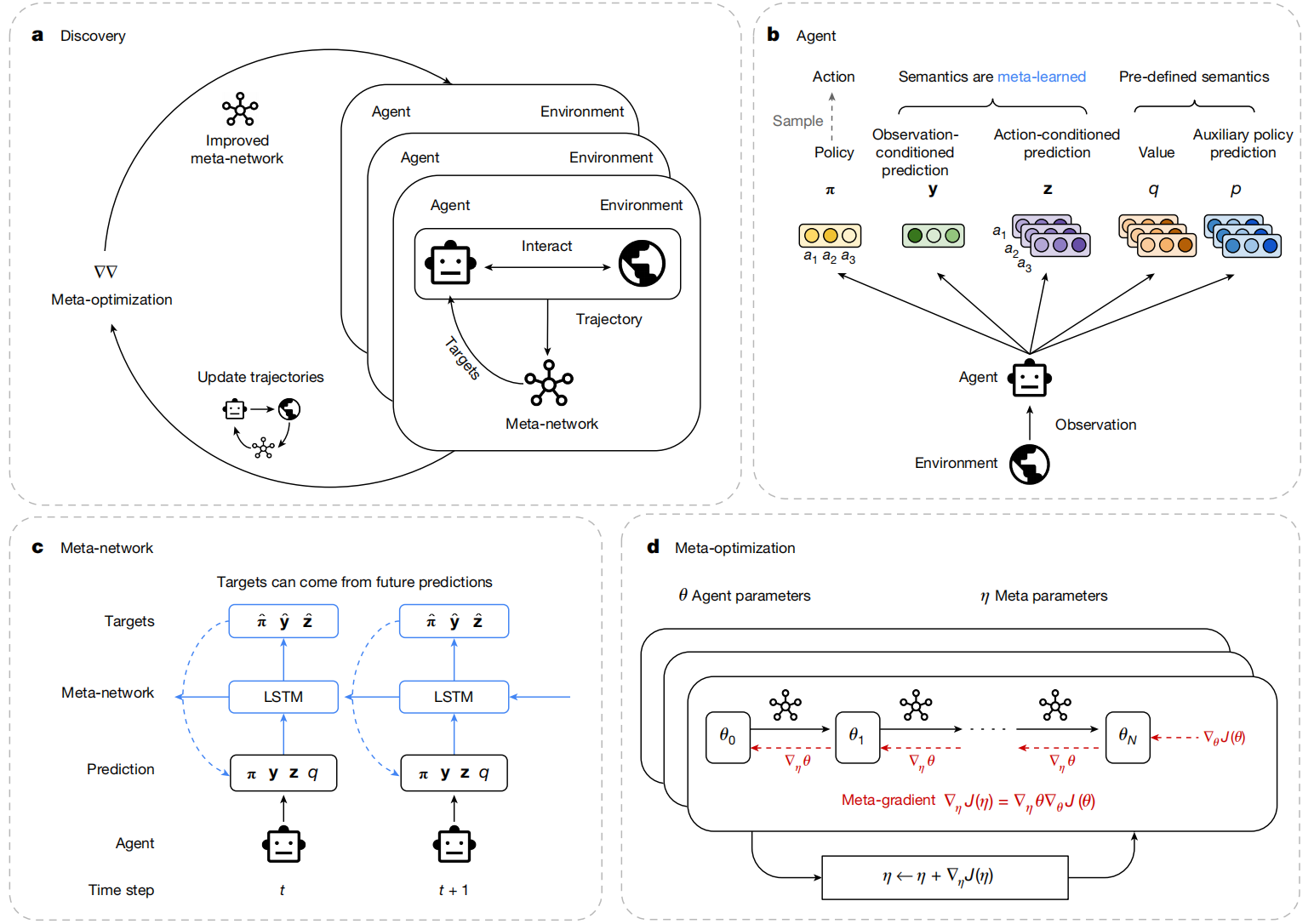图1｜从智能体群体中发现RL规则。a ，发现阶段。多个智能体在不同环境中并行交互，并按照由元网络定义的学习规则进行训练。与此同时，元网络被优化，以提升智能体群体的整体性能。b ，智能体结构。智能体产生以下输出：（1）策略（ π \pi π），（2）基于观测的预测向量（ y \mathbf{y} y），（3）基于动作的预测向量（ z \mathbf{z} z），（4）动作价值（ q \mathbf{q} q），以及（5）辅助策略预测（ p \mathbf{p} p）。 y \mathbf{y} y 和 z \mathbf{z} z 的语义由元网络决定。 c ，元网络结构。将智能体输出的轨迹连同来自环境的奖励和回合终止指示（为简洁起见，图中省略）作为输入送入元网络。元网络利用这些信息，为智能体在当前和未来时间步的所有预测生成目标。智能体通过最小化预测与目标之间的误差进行更新。 LSTM，长短期记忆网络。 d ，元优化。通过对智能体更新过程（ θ 0 → θ N \theta_0 \rightarrow \theta_N θ0→θN）进行反向传播计算元梯度，并据此更新元网络的元参数，其元目标是最大化智能体在环境中的整体回报。

图1a：Discovery（发现阶段）------"一群学生 + 一位教练"循环进化

把图1a读成一个故事：

有很多个智能体（agents），每个都在不同环境里玩（Atari、ProcGen、等等）。

每个智能体都按当前的"学习规则"去更新自己。

但这个"学习规则"不是人写的，而是由一个**元网络（meta-network）**给出来的。

然后系统会看：这一批智能体整体表现好不好（总回报高不高）。

如果不好，就用**元优化（meta-optimization）**去更新 meta-network，让它下次给出更好的学习规则。

如此循环：meta-network越来越会"教"，agents越来越会"学"。

一句话：
外层在训练"教练"（meta-network），内层在训练"学生"（agents）。

图1b：Agent（智能体结构）------它不是只输出动作，而是输出 5 类东西

图1b里智能体从环境拿到观测 o t o_t ot，然后吐出五个头（outputs）：

策略 π \pi π ：给出动作分布，用来采样动作 a t a_t at（你可以理解为"我现在要怎么动"）。

y \mathbf{y} y：基于观测的预测向量（observation-conditioned prediction）

z \mathbf{z} z：基于动作条件的预测向量（action-conditioned prediction）

q \mathbf{q} q：动作价值（value / action-value 一类，图里标成 value）

p \mathbf{p} p：辅助策略预测（auxiliary policy prediction）

关键点在图里写得很清楚：

q \mathbf{q} q、 p \mathbf{p} p 属于 pre-defined semantics（预定义语义）：它们大致对应"价值/辅助策略"这种传统 RL 常见概念。

y \mathbf{y} y、 z \mathbf{z} z 的语义是 meta-learned（元学习出来的语义） ：也就是说作者不规定 y \mathbf{y} y 一定是 value，不规定 z \mathbf{z} z 一定是 dynamics。它们只是"向量预测"，到底预测什么、怎么有用，由 meta-network 来决定。

你可以把 y , z \mathbf{y},\mathbf{z} y,z 当成两块"白板"：

白板上写什么（语义）不提前规定；

meta-network 会发明一种"写法"和"用法"，只要能让最终回报变高就行。

图1c：Meta-network（元网络）------它的工作就是"给目标 target"

传统 RL 的本质常常是这种形式：

你预测一个量（比如 value 或 Q），然后你定义一个 target（比如 TD target），再让网络去拟合它：预测 ≈ \approx ≈ target。

这篇论文把"target 怎么构造"这件事交给 meta-network。

1 meta-network 的输入是什么？

图注写了（图中为了简洁省略 reward/done，但实际会用）：

智能体在一段轨迹里输出的东西： ( π , y , z , q , p ) (\pi,\mathbf{y},\mathbf{z},\mathbf{q},\mathbf{p}) (π,y,z,q,p) 随时间的序列

环境给的：奖励 r t r_t rt、回合是否结束 d t d_t dt（done flag）

也就是：一整段"我怎么做的、环境怎么反馈的"的记录（trajectory）。

2 meta-network 的输出是什么？

图1c顶部写得很直白：

Targets can come from future predictions

meta-network（用 LSTM 做，因为要吃序列）会对每个时间步，输出一组"学习目标"：

例如对 y \mathbf{y} y 给一个目标 y ^ \hat{\mathbf{y}} y^

对 z \mathbf{z} z 给一个目标 z ^ \hat{\mathbf{z}} z^

甚至对策略也可以给某种目标/信号（图里也画了 π ^ \hat{\pi} π^）

注意：这些 target 可以用"未来的信息"来构造 ，比如用 t + 1 , t + 2 t+1,t+2 t+1,t+2 的预测、未来奖励等组合出来------这就是它能"发明新规则"的自由度来源。

3 智能体怎么用这些 target 更新？

智能体的内层学习就变成非常朴素的"拟合目标"：

对每个时间步 t t t，构造一个损失（示意）： L t = ∣ y t − y ^ t ∣ 2 + ∣ z t − z ^ t ∣ 2 + (policy/value/aux 的一些误差项) \mathcal{L}_t= |\mathbf{y}_t-\hat{\mathbf{y}}_t|^2+ |\mathbf{z}_t-\hat{\mathbf{z}}_t|^2+ \text{(policy/value/aux 的一些误差项)} Lt=∣yt−y^t∣2+∣zt−z^t∣2+(policy/value/aux 的一些误差项)

然后做梯度下降更新 agent 参数 θ \theta θ： θ ← θ − α ∇ θ ∑ t L t \theta\leftarrow\theta-\alpha\nabla_\theta\sum_t\mathcal{L}_t θ←θ−α∇θt∑Lt

所以：这篇论文所谓"RL规则"，本质上就是：meta-network 产生 target 的方式 + 智能体拟合 target 的方式。

图1d：Meta-optimization（元优化）------"教练怎么变强"？靠元梯度穿过学生的学习过程

这块是很多人卡住的点。我用一句话先定性：

meta-network 的目标不是让 target 看起来漂亮，而是让"按这些 target 学习后的 agent"，在环境里拿到更高回报。

1 两层参数

智能体参数： θ \theta θ（图1d左上写 θ \theta θ）

元网络参数： η \eta η（图1d右上写 η \eta η）

2 内层：智能体学习是一个"展开的更新链"

图1d里写的是： θ 0 → θ 1 → . . . → θ N \theta_0\rightarrow\theta_1\rightarrow...\rightarrow\theta_N θ0→θ1→...→θN 意思是：同一个 agent 训练 N N N 次更新，每次更新都用到了 meta-network 产生的 targets（所以每一步更新都"依赖 η \eta η"）。

3 外层：对"最终回报"反向传播，更新 η \eta η

他们做的是 unroll + backprop（把训练过程展开，然后反传）。

定义元目标：让最终回报 J J J 大（等价于最小化负回报）。

因为 θ N \theta_N θN 是通过多步更新得到的，而更新规则又由 η \eta η 决定，所以：

∇ η J ( η ) = ∇ η J ( θ N ( η ) ) \nabla_\eta J(\eta)=\nabla_\eta J(\theta_N(\eta)) ∇ηJ(η)=∇ηJ(θN(η))

图里红字表达的是"元梯度"要穿过 θ \theta θ 的更新链条（ θ 0 \theta_0 θ0 到 θ N \theta_N θN）。最后更新元网络参数（图底部）： η ← η + ∇ η J ( η ) \eta\leftarrow\eta+\nabla_\eta J(\eta) η←η+∇ηJ(η)

（符号正负取决于你写的是最大化回报还是最小化损失；图里写的是"加上梯度"表示最大化。）

为了选择一个具有普适性的发现空间，我们注意到：标准RL算法的核心组成部分是一种更新规则，它将一个或多个预测以及策略本身，更新到以未来奖励、未来预测等量为函数的目标上。基于不同目标构造的RL规则包括：时序差分学习¹⁶、Q-learning¹⁷、近端策略优化（PPO）¹⁸、辅助任务¹⁹、继承特征（successor features）²⁰以及分布式RL²¹。在每一种情况下，目标的选择决定了预测的性质，例如预测是价值函数、环境模型，还是继承特征。

在我们的框架中，RL规则由一个元网络（meta-network）表示，该网络决定智能体应将其预测和策略更新到何种目标（图1c）。这使系统能够在没有预定义语义的情况下发现有用的预测形式，以及这些预测应如何被使用。原则上，该系统可能重新发现已有的RL规则，但其灵活的函数形式也允许智能体发明全新的、可能针对特定环境而优化的RL规则。

在发现过程中，我们实例化了一组智能体群体，每个智能体都与来自多样化挑战任务集合中的一个环境实例进行交互。每个智能体的参数都按照当前的RL规则进行更新。随后，我们使用元梯度方法¹³逐步改进RL规则，使其能够产生性能更优的智能体。

我们的大规模实验结果表明，我们发现的RL规则（称为DiscoRL）在其进行元学习的环境中超过了所有已有的RL规则。值得注意的是，这其中包括Atari游戏²²------它被广泛认为是最成熟、信息量最大的RL基准之一。此外，DiscoRL在若干其他具有挑战性的基准（如ProcGen²³）上也取得了最先进的性能，而这些基准在发现阶段从未被接触过。我们还表明，随着在发现阶段引入更加多样和复杂的环境，DiscoRL的性能和通用性会进一步提升。最后，我们的分析显示，DiscoRL发现了独特的预测语义，这些语义不同于诸如价值函数等已有的RL概念。据我们所知，这是首次在实验上证明：在通用性和效率两个方面超越人工设计RL算法已触手可及。

RL规则的本质：就是"你预测什么 + target怎么定义 + 怎么更新参数"。

这篇论文把 target 的定义交给 meta-network：meta-network 输出 targets，agent 拟合它们。

agent 不是只输出动作 ：还输出 y , z , q , p \mathbf{y},\mathbf{z},\mathbf{q},\mathbf{p} y,z,q,p 多个头，用来承载更丰富的"可被利用的预测"。

y , z \mathbf{y},\mathbf{z} y,z 没有预定义语义：语义是 meta-learned 的------这是"能发明新概念"的关键设计。

元优化（meta-gradient） ：meta-network 的更新信号来自"学完之后回报是否更高"，梯度要穿过 θ 0 → . . . → θ N \theta_0\rightarrow...\rightarrow\theta_N θ0→...→θN 的更新链条。

大规模并行 agent+环境：用群体表现来训练"教练"（meta-network），让发现的规则更稳、更泛化。

Discovery method

我们的发现方法包含两类优化：智能体优化（agent optimization）与元优化（meta-optimization）。智能体的参数通过更新其策略与预测，使其朝向由RL规则产生的目标来进行优化。与此同时，RL规则的元参数通过更新其生成的目标来进行优化，以最大化智能体的累积回报。

你可以把系统想成：

学生（agent）：在环境里玩游戏、拿奖励、学会更聪明。

教练（meta-network） ：不直接玩游戏，它只做一件事：告诉学生"你应该把哪些输出往什么目标(target)靠拢"。

两种优化同时发生：

Agent optimization ：学生更新自己参数 θ \theta θ，让自己的输出更像教练给的 target。

Meta-optimization ：教练更新自己参数 η \eta η，让它"给出的 target"能让学生最后拿到更高回报。

一句话： 学生学怎么做动作；教练学怎么教学生。

Agent network

传统 RL 往往只规定：你输出一个策略 π ( a ∣ s ) \pi(a|s) π(a∣s)（或再加 value），然后用人写的 TD / PPO / PG 去训练。这篇不这么干。它让 agent 输出一堆东西：

大量RL研究会考虑智能体应该做出哪些预测（例如价值），以及应该使用什么损失函数来学习这些预测（例如时序差分（TD）学习）并改进策略（例如策略梯度）。不同于手工设计这些内容，我们定义了一个没有预定义语义、但表达能力很强的预测空间，并用一个元网络来表征，从而通过元学习自动学出智能体需要优化的内容。我们希望在支持大量新算法可能性的同时，仍能保持对现有RL算法关键思想的表达能力。

1 必输出：策略 π \pi π

π θ ( s ) \pi_\theta(s) πθ(s)：看到状态/观测 s s s 后，给出动作分布，用来采样动作 a a a。

为此，我们让由参数 θ \theta θ 表示的智能体在输出策略 π \pi π 之外，还输出两类预测：一个基于观测条件的向量预测 y ( s ) ∈ R n \mathbf{y}(s)\in\mathbb{R}^n y(s)∈Rn（维度 n n n 可任意设定），以及一个基于动作条件的向量预测 z ( s , a ) ∈ R m \mathbf{z}(s,a)\in\mathbb{R}^m z(s,a)∈Rm（维度 m m m 可任意设定）；其中 s s s 与 a a a 分别表示观测与动作（图1b）。这些预测的形式源于"预测（prediction）与控制（control）"之间的基本区分¹⁶。例如，价值函数通常被划分为状态价值函数 v ( s ) v(s) v(s)（用于预测）与动作价值函数 q ( s , a ) \mathbf{q}(s,a) q(s,a)（用于控制）；而RL中的许多其他概念（例如奖励、继承特征 successor features）也同样存在基于观测条件的版本与基于动作条件的版本。因此，预测 ( y , z ) (\mathbf{y},\mathbf{z}) (y,z) 的函数形式足够通用，能够表示（但并不局限于）RL中许多已有的基本概念。

2 关键创新：两类"无语义预测" y , z \mathbf{y},\mathbf{z} y,z

它们是没有预定义语义的向量（你不要强行把它当成 value 或 model）。

y θ ( s ) ∈ R n \mathbf{y}_\theta(s)\in\mathbb{R}^n yθ(s)∈Rn：基于观测条件的向量预测

输入只看 s s s，输出一个长度 n n n 的向量。

n n n 可以任意设（你可以理解成"我给你 n n n 个槽位，让你自己学出有用的预测特征"）。

z θ ( s , a ) ∈ R m \mathbf{z}_\theta(s,a)\in\mathbb{R}^m zθ(s,a)∈Rm：基于动作条件的向量预测

输入看 ( s , a ) (s,a) (s,a)，输出一个长度 m m m 的向量。

m m m 也任意设。

为什么要分成"只看 s s s"和"看 ( s , a ) (s,a) (s,a)"两类？原文说这来自 RL 里"prediction vs control"的基本区分：

很多东西天然有两种版本，比如：

状态价值 v ( s ) v(s) v(s)（只看 s s s）

动作价值 q ( s , a ) q(s,a) q(s,a)（看 s , a s,a s,a） successor features、奖励等也能做成两种版本。

所以他们设计 y , z \mathbf{y},\mathbf{z} y,z 这种形式，是为了足够通用：既能表达传统概念，也能容纳新概念。

除了需要被发现的那些预测之外，在我们的大多数实验中，智能体还会进行一些具有预定义语义的预测。具体来说，智能体会输出一个动作价值函数 q ( s , a ) \mathbf{q}(s,a) q(s,a)，以及一个以动作为条件的辅助策略预测 p ( s , a ) \mathbf{p}(s,a) p(s,a)⁸。这会促使发现过程主要通过 y \mathbf{y} y 和 z \mathbf{z} z 来聚焦于发现新的概念。

3 另外还有"有预定义语义"的输出： q , p \mathbf{q},\mathbf{p} q,p

这段话非常关键：作者不希望整个发现过程都被"重新发明 value/Q"占满，所以他们给 agent 额外输出两项传统东西，让它们"有专门的通道"，把创新压力集中到 y , z \mathbf{y},\mathbf{z} y,z 上。

q θ ( s , a ) \mathbf{q}_\theta(s,a) qθ(s,a)：动作价值（有语义）

p θ ( s , a ) \mathbf{p}_\theta(s,a) pθ(s,a)：以动作为条件的辅助策略预测（有语义）

Meta-network（元网络）

你可以把一切现代 RL 都看成一句话：

你预测一些东西，然后你构造 target（经常用未来信息自举），然后逼近 target 来更新网络。

比如 TD 的 target 就是 " r + γ v ( s ′ ) r+\gamma v(s') r+γv(s′)"。 PPO/PG 也有各种"目标/基线/优势"在指导更新。这篇论文的核心：target 不由人写，由 meta-network 学出来。

现代RL规则中有相当大一部分采用RL的 前向视角（forward view） ¹⁶。在这种视角下，RL规则接收从时间步 t t t 到 t + n t+n t+n 的一段轨迹，并利用这段信息来更新智能体的预测或策略。它们通常将预测或策略朝向自举（bootstrapped）目标进行更新，也就是朝向未来预测所构成的目标进行更新。

1 "前向视角 forward view"是啥（原文强调）

forward view 的意思很朴素：为了更新时间步 t t t 的东西，你会看从 t t t 到 t + n t+n t+n

的一段轨迹（未来几步），用这段信息来构造目标。这就是 n-step return、GAE、Retrace 等一大类方法的共同味道：目标用未来几步信息拼出来。

相应地，我们的RL规则使用一个元网络（图1c）作为函数，用于确定智能体应将其预测与策略更新到的目标。为了在时间步 t t t 生成目标，元网络接收从 t t t 到 t + n t+n t+n 的输入，包括：智能体预测与策略的轨迹，以及奖励与回合终止信息。元网络使用标准的长短期记忆网络（LSTM）²⁴来处理这些输入，不过也可以使用其他结构（扩展数据图3）。

元网络输入与输出的设计保留了人工设计RL规则的一些理想性质。第一，元网络能够处理任意形式的观测，并且能够适配任意大小的离散动作空间。之所以可行，是因为元网络并不直接把观测作为输入，而是仅通过预测量间接获得与观测相关的信息。此外，它通过在动作维度之间共享权重来处理与具体动作相关的输入与输出。因此，它能够泛化到差异极大的环境中。第二，元网络对智能体网络的具体设计是不敏感的，因为它只"看到"智能体网络的输出。只要智能体网络能产生所需形式的输出（ π , y , z \pi, \mathbf{y}, \mathbf{z} π,y,z），所发现的RL规则就能泛化到任意智能体结构或规模。第三，元网络所定义的搜索空间包含了自举（bootstrapping）这一重要算法思想。第四，由于元网络同时处理策略与预测，它不仅可以元学习辅助任务²⁵，还能直接利用预测来更新策略（例如提供一个基线以降低方差）。最后，输出"目标"在表达能力上严格强于输出一个标量损失函数，因为这会把诸如Q-learning这样的半梯度方法也纳入搜索空间。在继承标准RL算法这些性质的同时，这种参数化能力很强的神经网络还能使所发现的规则实现可能更高效、并且更具上下文细腻性的算法。

2 meta-network 的输入是什么？

为了给时间步 t t t 生成 target，它吃一段轨迹（ t → t + n t\rightarrow t+n t→t+n）：

agent 在这段里输出的： π , y , z , ( q , p ) \pi,\mathbf{y},\mathbf{z},(\mathbf{q},\mathbf{p}) π,y,z,(q,p)

环境给的：奖励 r r r、终止 done

注意一个设计： meta-network 不直接看原始观测 s s s ，它只看 agent 的输出（预测/策略）+ reward/done。原文说这样做的好处是：能适配各种观测形式，并对 agent 架构不敏感。
3 meta-network 的结构为什么用 LSTM？

因为它吃的是"时间序列轨迹"，LSTM 擅长处理序列记忆。（原文也说可以换别的结构，但实现用 LSTM。）

4 meta-network 的输出是什么？

它输出的是 targets：

π ^ \hat{\pi} π^：策略该朝哪儿更新（一个目标分布）

y ^ \hat{\mathbf{y}} y^： y \mathbf{y} y 该朝哪儿更新（一个目标向量分布）

z ^ \hat{\mathbf{z}} z^： z \mathbf{z} z 该朝哪儿更新

以及辅助项的 q ^ , p ^ \hat{\mathbf{q}},\hat{\mathbf{p}} q^,p^（后面会讲它们怎么来）

你要把"输出 target"理解成：
教练不是说"你这题错了扣几分"（标量 loss），而是直接给你"标准答案是什么"（target） 。原文强调：输出 target 的表达能力比输出一个标量损失更强，因为像 Q-learning 的"半梯度"类更新很难用简单标量 loss 完整覆盖，但用 target 可以覆盖得更广。

Agent optimization

智能体的参数（ θ \theta θ）通过最小化其预测和策略与元网络所生成目标之间的距离来进行更新。智能体的损失函数可以表示为：

L ( θ ) = E s , a ∼ π θ [ D ( π ^ , π θ ( s ) ) + D ( y ^ , y θ ( s ) ) + D ( z ^ , z θ ( s , a ) ) + L aux ] L(\theta)= \mathbb{E}{s,a\sim\pi\theta} \Big[ D(\hat{\pi},\pi_\theta(s)) + D(\hat{\mathbf{y}},\mathbf{y}\theta(s)) + D(\hat{\mathbf{z}},\mathbf{z}\theta(s,a)) + L_{\text{aux}} \Big] L(θ)=Es,a∼πθ[D(π^,πθ(s))+D(y^,yθ(s))+D(z^,zθ(s,a))+Laux]

把它读成人话就是：

从当前策略 π θ \pi_\theta πθ 采样到状态 s s s、动作 a a a，然后让：

你的策略输出 π θ ( s ) \pi_\theta(s) πθ(s) 贴近教练给的 π ^ \hat{\pi} π^

你的 y θ ( s ) \mathbf{y}_\theta(s) yθ(s) 贴近教练给的 y ^ \hat{\mathbf{y}} y^

你的 z θ ( s , a ) \mathbf{z}_\theta(s,a) zθ(s,a) 贴近教练给的 z ^ \hat{\mathbf{z}} z^

再加上辅助损失 L aux L_{\text{aux}} Laux

其中， s s s 和 a a a 按照策略 π θ \pi_\theta πθ 的分布采样， D ( p , q ) D(\mathbf{p},\mathbf{q}) D(p,q) 表示 p \mathbf{p} p 与 q \mathbf{q} q 之间的距离函数。我们选择 Kullback--Leibler（KL）散度作为距离函数，因为它具有足够的通用性，并且已有研究发现它能使元优化过程更容易³。其中， π θ , y θ , z θ \pi_\theta, \mathbf{y}\theta, \mathbf{z}\theta πθ,yθ,zθ 分别是智能体网络的输出，而 π ^ , y ^ , z ^ \hat{\pi}, \hat{\mathbf{y}}, \hat{\mathbf{z}} π^,y^,z^ 是元网络的输出；对每个向量都应用 softmax 函数进行归一化。

原文说：用 KL 是因为通用，而且以前工作发现它让元优化更容易。实现细节：他们对每个向量都做 softmax 归一化，所以这些东西都变成"概率分布"，KL 就合理了。

直觉：把 y , z \mathbf{y},\mathbf{z} y,z 当成"分类分布"一样去对齐目标，会让梯度性质更稳定、更适合穿过元梯度链路。

辅助损失 L aux L_{\text{aux}} Laux 用于具有预定义语义的预测，即动作价值 q \mathbf{q} q 和辅助策略预测 p \mathbf{p} p，其形式如下：

L aux = D ( q ^ , q θ ( s , a ) ) + D ( p ^ , p θ ( s , a ) ) L_{\text{aux}} = D(\hat{\mathbf{q}}, \mathbf{q}\theta(s,a)) + D(\hat{\mathbf{p}}, \mathbf{p}\theta(s,a)) Laux=D(q^,qθ(s,a))+D(p^,pθ(s,a))

其中， q ^ \hat{\mathbf{q}} q^ 是由 Retrace²⁶ 算法得到的动作价值目标，并被投影为 two-hot 向量⁸； p ^ = π θ ( s ′ ) \hat{\mathbf{p}}=\pi_\theta(s') p^=πθ(s′) 表示一步未来状态 s ′ s' s′ 下的策略。为了与其余损失项保持一致，我们同样使用 KL 散度作为距离函数 D D D。

q ^ \hat{\mathbf{q}} q^：用 Retrace 算出来的动作价值 target，并投影成 two-hot（这是一种把标量值分布化/离散化的编码方式）

p ^ = π θ ( s ′ ) \hat{\mathbf{p}}=\pi_\theta(s') p^=πθ(s′)：下一步状态 s ′ s' s′ 的策略分布当作目标（所以 p \mathbf{p} p 学的是"如果到了下一步，你的策略会是什么样"）

所以：
q , p \mathbf{q},\mathbf{p} q,p 这两项并不是 meta-network 发明的语义，而是传统、稳定的学习信号 ，帮助训练更稳，同时让"新东西主要从 y , z \mathbf{y},\mathbf{z} y,z 里长出来"。

Meta-optimization（元优化）

1 每个符号到底什么意思

η \eta η：meta-network（教练）的参数

θ \theta θ：agent（学生）的参数

E \mathcal{E} E：环境分布（很多环境）

J ( θ ) = E [ ∑ t γ t r t ] J(\theta)=\mathbb{E}[\sum_t \gamma^t r_t] J(θ)=E[∑tγtrt]：学生在环境里的期望折扣回报（标准 RL 目标）

所以 J ( η ) J(\eta) J(η) 的意思是：

在很多环境里，按教练规则训练出来的学生，平均能拿到多少回报。

教练要做的是：让这个平均回报最大。

我们的目标是发现一条由元网络表示、其元参数为 η \eta η 的RL规则，使智能体能够在多种训练环境中最大化回报。该发现目标 J ( η ) J(\eta) J(η) 及其元梯度 ∇ η J ( η ) \nabla_\eta J(\eta) ∇ηJ(η) 可表示为：

J ( η ) = E E E θ [ J ( θ ) ] , ∇ η J ( η ) ≈ E E E θ [ ∇ η θ ∇ θ J ( θ ) ] J(\eta)=\mathbb{E}{\mathcal{E}}\mathbb{E}{\theta}[J(\theta)], \qquad \nabla_\eta J(\eta)\approx \mathbb{E}{\mathcal{E}}\mathbb{E}{\theta} \big[\nabla_\eta \theta \, \nabla_\theta J(\theta)\big] J(η)=EEEθ[J(θ)],∇ηJ(η)≈EEEθ[∇ηθ∇θJ(θ)]

其中， E \mathcal{E} E 表示从某一分布中采样得到的环境， θ \theta θ 表示由初始参数分布以及在RL规则作用下随学习过程演化得到的智能体参数。 J ( θ ) = E [ ∑ t γ t r t ] J(\theta)=\mathbb{E}\left[\sum_t \gamma^t r_t\right] J(θ)=E[∑tγtrt] 表示期望折扣回报之和，其中 γ \gamma γ 是折扣因子， r t r_t rt 是时间步 t t t 的奖励；这是典型的RL优化目标。元参数按照上述公式，使用梯度上升法进行优化。

2 元梯度为什么是 ∇ η θ , ∇ θ J ( θ ) \nabla_\eta \theta ,\nabla_\theta J(\theta) ∇ηθ,∇θJ(θ) 这种形式？

这是链式法则：

教练参数 η \eta η 会影响教练输出的 targets

targets 会影响学生更新过程

学生更新后的参数 θ \theta θ 会影响最终回报 J ( θ ) J(\theta) J(θ)

所以梯度要拆成两段：

∇ η θ \nabla_\eta \theta ∇ηθ：教练改一点点，会让学生最终参数怎么变（对"学习过程"的梯度）

∇ θ J ( θ ) \nabla_\theta J(\theta) ∇θJ(θ)：学生参数变一点点，回报怎么变（标准 RL 的梯度）

两者乘起来就是"教练通过影响学生，最终影响回报"的方向。

为了估计元梯度，我们在一组采样得到的环境中实例化一群按照元网络进行学习的智能体。为确保该近似尽可能接近真实关注的分布，我们使用来自具有挑战性基准的大量复杂环境，这不同于以往仅关注少量简单环境的工作。因此，发现过程能够自然暴露多样的RL挑战，例如奖励稀疏性、任务时间跨度，以及环境的部分可观测性或随机性。

每个智能体的参数会被周期性地重置，以促使更新规则在有限的智能体生命周期内实现快速学习进展。与先前关于元梯度RL的工作¹³类似，元梯度项 ∇ η J ( η ) \nabla_\eta J(\eta) ∇ηJ(η) 可通过链式法则分解为两项： ∇ η θ \nabla_\eta \theta ∇ηθ 和 ∇ θ J ( θ ) \nabla_\theta J(\theta) ∇θJ(θ)。第一项可理解为对智能体更新过程本身的梯度²⁷，而第二项则是标准RL目标的梯度。为估计第一项，我们对智能体进行多次迭代更新，并对整个更新过程进行反向传播，如图1d所示。为保证计算可行性，我们采用滑动窗口的方式，对连续20次智能体更新进行反向传播。最后，为估计第二项，我们采用优势行动者--评论家（advantage actor--critic, A2C）方法²⁸。为了估计优势函数，我们训练了一个元价值函数（meta-value function），该价值函数仅用于发现过程。

3 ∇ η θ \nabla_\eta \theta ∇ηθ 怎么算？------把学生的学习过程"展开+反传"

原文说：

对智能体进行多次迭代更新

对整个更新过程反向传播（图1d）

为了算得动，用滑动窗口，只对连续 20 次更新做反传（truncated BPTT / sliding window）

这句话你一定要理解成：

教练要学会怎么教，就必须知道"如果我给你这种 target，你学 20 步之后会变强还是变弱"。于是把这 20 步更新当成计算图的一部分，反向传播回去更新教练。

4 ∇ θ J ( θ ) \nabla_\theta J(\theta) ∇θJ(θ) 怎么算？------用 A2C

原文说第二项用 A2C 来估计。 A2C 需要优势函数 A ( s , a ) A(s,a) A(s,a)，所以他们训练一个 meta-value
function（只在发现阶段用），来提供优势估计。你可以理解成：

学生在环境里跑出来的轨迹，用 A2C 方式给出"哪些动作是好贡献"的梯度信号；

这个信号再通过"学生更新链"传回教练。
把整段话浓缩成"你脑子里该有的运行画面"（最重要）

一次 discovery 迭代大概像这样：

采样很多复杂环境（为了覆盖奖励稀疏、长时程、部分可观测、随机等挑战）。

每个环境放一个学生 agent。

学生用当前策略交互，收集轨迹。

教练 meta-network 看轨迹（含奖励/终止 + 学生的输出序列），给每个时间步吐 targets： π ^ , y ^ , z ^ \hat{\pi},\hat{\mathbf{y}},\hat{\mathbf{z}} π^,y^,z^（以及 aux targets）。

学生用 KL 距离把自己的输出对齐 targets，更新 θ \theta θ（重复多次）。

评估学生回报，用 A2C 得到 ∇ θ J ( θ ) \nabla_\theta J(\theta) ∇θJ(θ)。

把学生最近 20 次更新"展开"，反向传播得到 ∇ η θ \nabla_\eta \theta ∇ηθ，再乘上 ∇ θ J ( θ ) \nabla_\theta J(\theta) ∇θJ(θ)，更新教练参数 η \eta η。

周期性重置学生参数，让规则必须在"短生命周期"里也能快速学出东西（逼着教练学会真正有效的更新规则，而不是靠长时间慢慢磨）。

最后就得到一个 DiscoRL 规则：也就是一个训练好的 meta-network，它能在新任务上当"教练"，指导新 agent 学得更快。

Empirical result（实证结果）

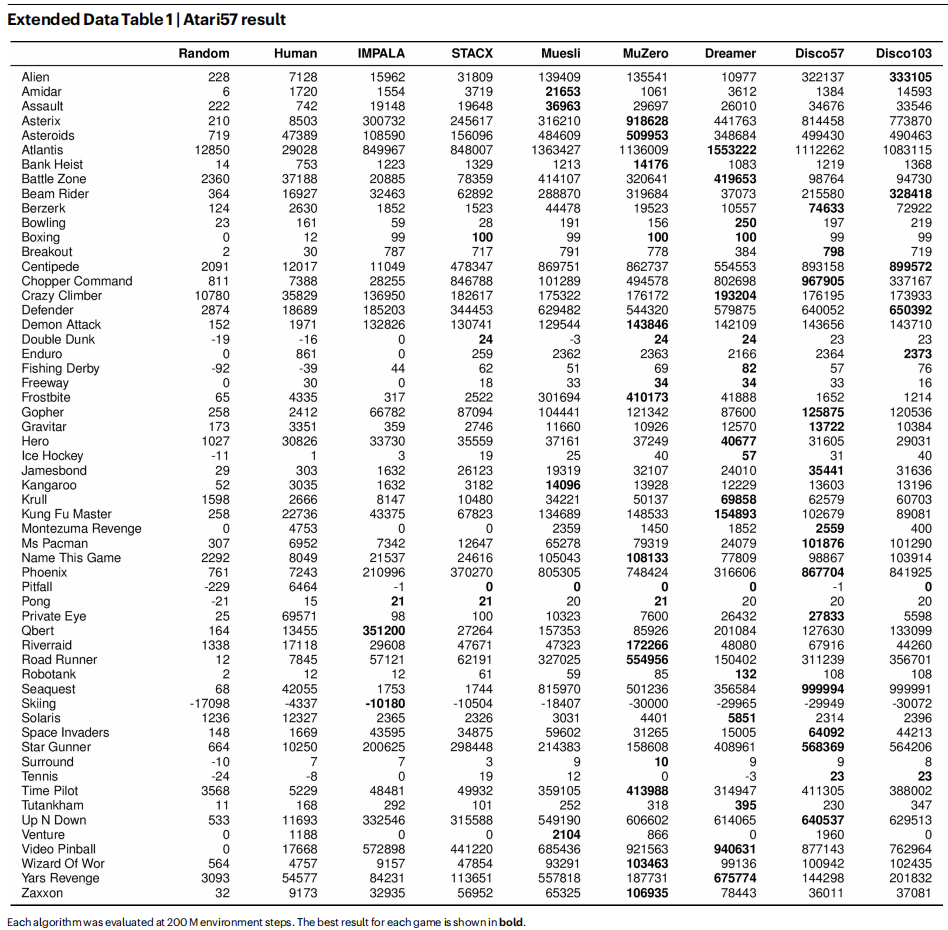
我们在一组复杂环境中，用大量智能体群体实现了我们的发现方法。我们将发现得到的RL规则命名为DiscoRL。在评估中，对于由多个任务组成的基准，我们用归一化分数的四分位均值（interquartile mean, IQM）来衡量总体性能；该指标已被证明在统计上是可靠的²⁹。

Atari

Atari基准²²是RL历史上研究最多的基准之一，由57个Atari 2600游戏组成。这些游戏需要复杂策略、规划能力以及长期信用分配，因此AI智能体要掌握它们并非易事。在过去十年里，已有数百种RL算法在该基准上被评测，其中包括MuZero⁸和Dreamer¹⁰。

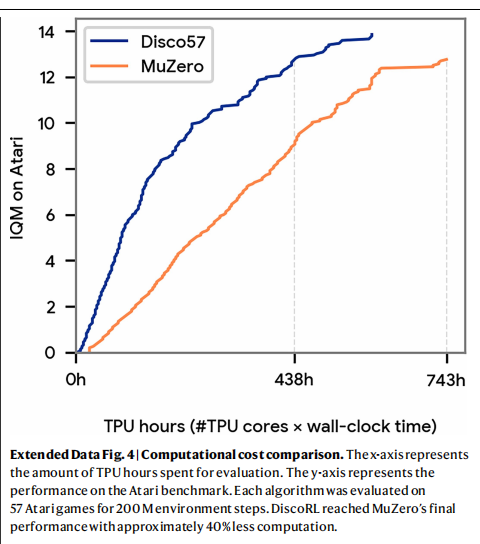
为了检验当规则直接从该基准中被发现时能有多强，我们元训练了一条RL规则Disco57，并在同样的57个游戏上进行评估（图2a）。在该评估中，我们使用的网络结构，其参数量与MuZero所用网络相当。该网络比发现阶段使用的网络更大；因此，所发现的RL规则必须能够泛化到这一设定下。 Disco57取得了13.86的IQM，在Atari基准上超过了所有已有RL规则⁸,¹⁰,¹⁴,³⁰，并且相较最先进的MuZero具有显著更高的真实时间（wall-clock）效率（扩展数据图4）。这表明，我们的方法能够从如此具有挑战性的环境中自动发现强大的RL规则。

Fig. 2 | Evaluation of DiscoRL（图2｜DiscoRL的评估） a--f，比较DiscoRL与人类设计的RL规则在Atari（a）、ProcGen（b）、DMLab（c）、Crafter（d；插图显示100万环境步结果）、NetHack（e）以及Sokoban（f）上的性能。横轴表示环境步数（单位：百万）。纵轴表示：对多任务基准（Atari、ProcGen、DMLab-30）的"按人类归一化的IQM分数"，以及对其余基准的平均回报。 Disco57（蓝色）从Atari基准中发现；Disco103（橙色）从Atari、ProcGen与DMLab-30基准中发现。阴影区域表示95%置信区间。虚线表示人工设计的RL规则，例如MuZero⁸、基于高效记忆的探索智能体（MEME）³⁰、Dreamer¹⁰、自调节行动者-评论家算法（STACX）¹⁴、重要性加权的actor-learner架构（IMPALA）³⁴、深度Q网络（DQN）⁵¹、分阶段策略梯度（PPG）⁵²、近端策略优化（PPO）¹⁸以及Rainbow⁵³。

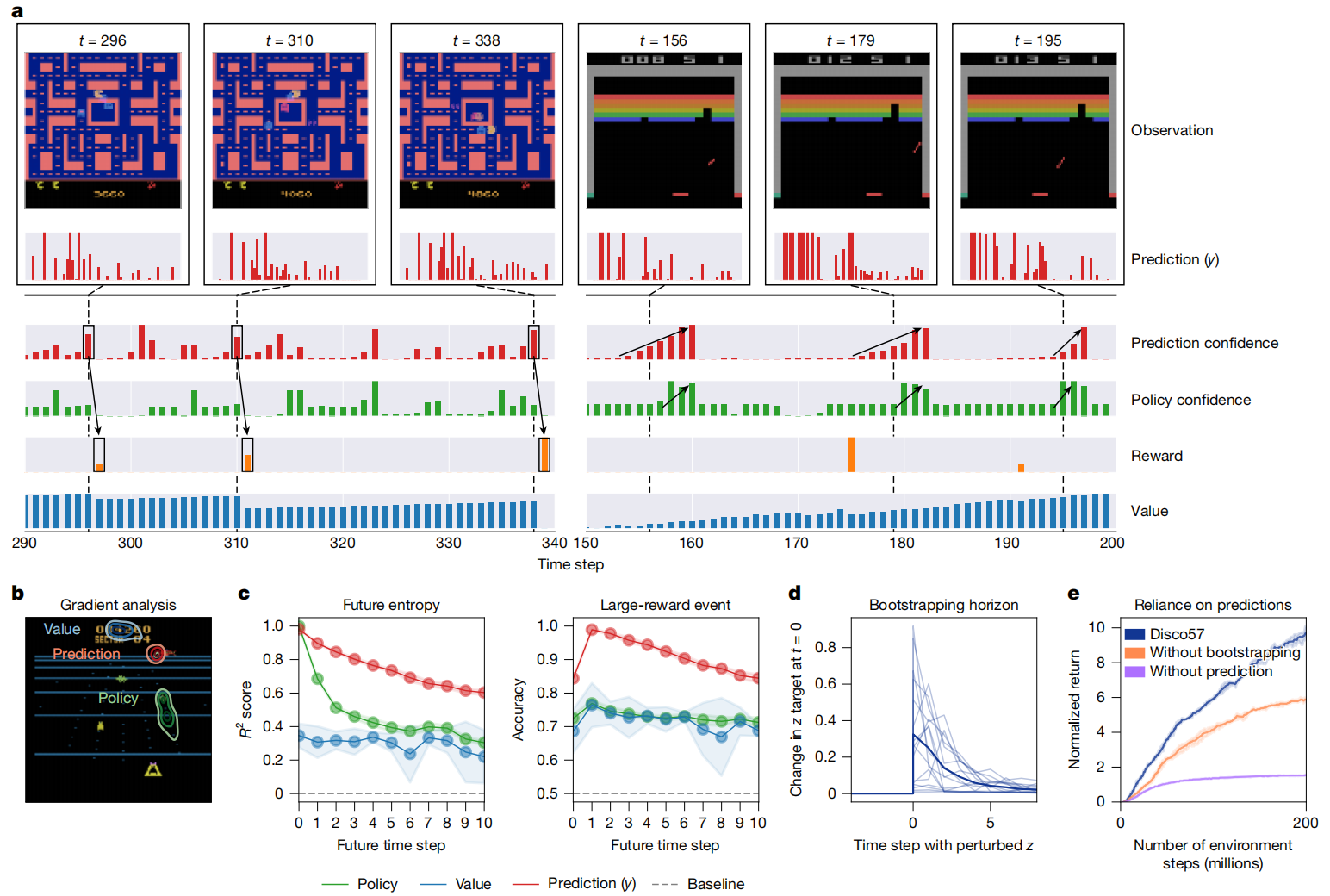图4｜DiscoRL的分析。 a，所发现预测的行为。该图展示了在《Ms Pacman》（左）与《Breakout》（右）中，智能体所发现的预测（ y y y）如何随其他量一起变化。 "置信度（Confidence）"通过**负熵（negative entropy）**计算得到。预测置信度的尖峰与即将发生的显著事件相关。例如，在《Ms Pacman》中，这些尖峰往往出现在大奖励之前；在《Breakout》中，它们往往出现在强烈动作偏好出现之前。 b，梯度分析。在《Beam Rider》中，通过梯度分析，每条等高线显示每个预测在观测中关注的位置。这些预测更倾向于关注远处的敌人；而策略与价值则分别更倾向于关注近处的敌人以及计分板。 c，预测分析。利用所发现的预测，可以更好地预测未来的熵以及大额奖励事件。阴影区域表示95%置信区间。 d，自举视野（bootstrapping horizon）。该图展示：当对每个时间步的预测进行扰动时，DiscoRL产生的预测目标会发生多大变化。每条细曲线对应16条随机采样轨迹中的一条，粗线表示它们的平均值。 e，对预测的依赖程度。该图展示在《Ms Pacman》中，对受控的DiscoRL进行评估时：一种情况是在更新预测时不使用自举，另一种情况是完全不使用预测；并比较其性能。阴影区域表示95%置信区间。

Generalization（泛化性）

我们进一步通过在多种发现阶段从未接触过的保留基准上进行评估，研究了Disco57的泛化能力。这些基准涵盖了未见过的观测与动作空间、多样的环境动力学、不同的奖励结构，以及未见过的智能体网络结构。元训练的超参数仅在训练环境（即Atari）上进行调节，以避免该规则被隐式地针对保留基准进行优化。

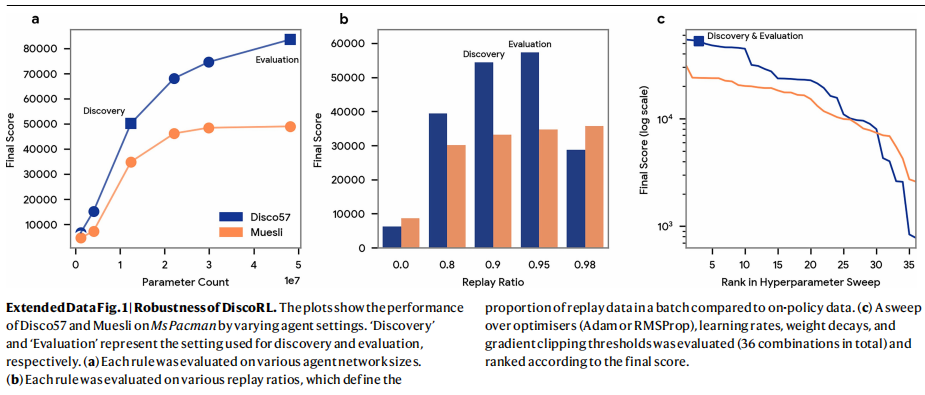
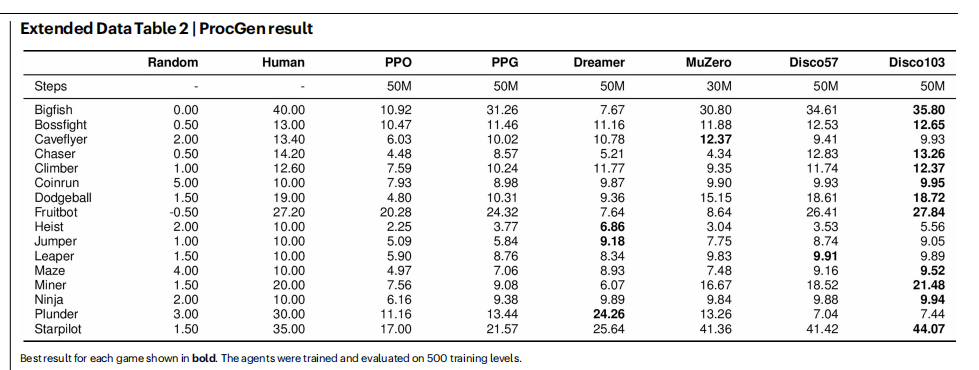
在ProcGen基准²³（图2b与扩展数据表2）上的结果表明：该基准由16个程序生成的二维游戏组成，尽管Disco57在发现阶段从未与ProcGen环境交互，但其性能仍超过了所有已发表的方法，包括MuZero⁸和PPO¹⁸。此外，Disco57在Crafter³¹（图2d与扩展数据表5）上取得了具有竞争力的性能；在该环境中，智能体需要学习广泛多样的能力才能生存。 Disco57在NetHack NeurIPS 2021 Challenge³²的排行榜上获得第三名（图2e与扩展数据表4），该比赛有40多个团队参与。与比赛中排名靠前的提交智能体³³不同，Disco57在定义子任务或奖励塑形时未使用任何领域特定知识。为进行公平比较，我们在与Disco57相同的设置下，训练了一个采用重要性加权actor-learner架构（IMPALA）³⁴的智能体。 IMPALA的性能明显更弱，这表明Disco57发现了一种比标准方法更高效的RL规则。除了对环境的泛化外，Disco57在评估中还对多种智能体相关设置表现出鲁棒性，例如网络规模、回放比例以及超参数（扩展数据图1）。

Complex and diverse environments（复杂且多样的环境）

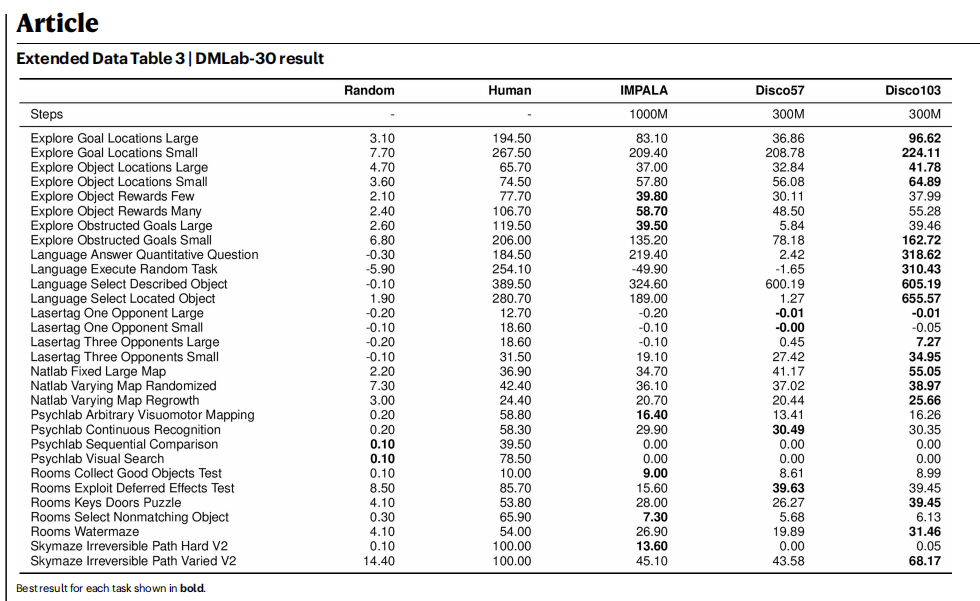
为理解复杂且多样环境在发现过程中的重要性，我们进一步通过引入更多环境来扩大元学习规模。具体而言，我们使用由Atari、ProcGen和DMLab-30³⁵组成的、更为多样的103个环境，发现了另一条规则Disco103。该规则在Atari基准上的表现与之前相当，但在图2中展示的所有其他已见与未见基准上均取得了更高分数。尤其值得注意的是，Disco103在Crafter上达到了人类水平，并在Sokoban³⁶上接近MuZero的最先进性能。这些结果表明：用于发现的环境集合越复杂、越多样，所发现的规则就越强、越具泛化性，甚至在发现阶段未见过的保留环境中亦是如此。与Disco57相比，发现Disco103并不需要对发现方法本身作任何修改，唯一变化只是环境集合。这表明发现过程本身是鲁棒、可扩展且通用的。

为进一步研究复杂环境的重要性，我们在57个由先前工作³扩展而来的网格世界任务上运行了发现过程，并使用与Disco57相同的元学习设置。该新规则在Atari基准上的性能显著更差（图3c）。这验证了我们关于直接从复杂且具有挑战性的环境中进行元学习至关重要的假设。尽管使用这类环境至关重要，但并不需要精心挑选"正确"的环境集合；我们只是使用了文献中常见的流行基准。

Efficiency and scalability（效率与可扩展性）

为进一步理解该方法的可扩展性与效率，我们在发现过程中评估了多个Disco57（图3a）。最优规则在每个Atari游戏约6亿步内被发现，这相当于在57个Atari游戏上仅进行3次实验。这在效率上显然优于人工发现RL规则的方法；后者通常需要执行更多实验，并投入大量研究人员时间。

此外，随着用于发现的Atari游戏数量增加，DiscoRL在未见过的ProcGen基准上的表现也随之提升（图3b），表明所发现的RL规则能够很好地随环境数量与多样性扩展。换言之，所发现规则的性能是数据（即环境）与算力的函数。

Effect of discovering new predictions（发现新预测的影响）

为研究所发现预测语义（图1b中的 y , z y,z y,z）的作用，我们通过改变智能体输出、是否包含某些类型预测来比较不同规则。图3c的结果表明，使用价值函数能显著改善发现过程，突出了这一RL基本概念的重要性。然而，图3c也显示：在预定义预测之外，发现新的预测语义（ y , z y,z y,z）同样至关重要。总体而言，相比先前工作¹--⁶，扩大"发现"的范围是至关重要的。在接下来的部分中，我们将进一步分析所发现的预测语义。

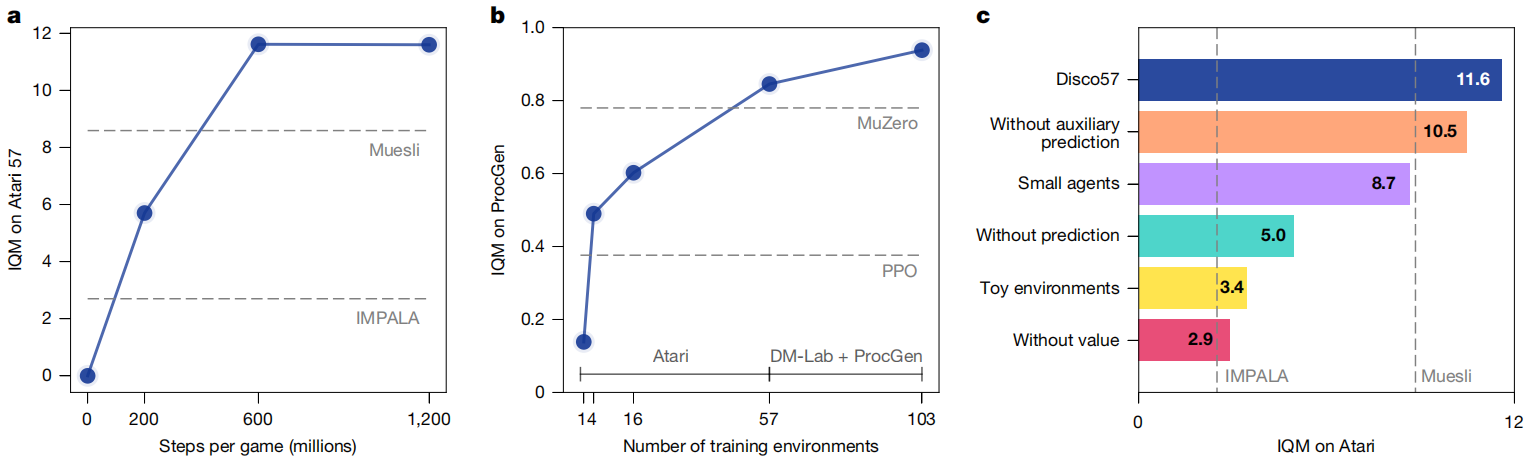Fig. 3 | Properties of discovery process（图3｜发现过程的性质） a，发现效率。最优的DiscoRL在每个游戏上仅用3次智能体生命周期的模拟（2亿步）就被发现。 b，可扩展性。随着训练环境集合变大，DiscoRL在ProcGen基准上的表现更强（所有方法均使用3000万环境步）。 c，消融实验。该图展示了DiscoRL不同变体在Atari上的性能。 "Without auxiliary prediction"表示在元学习时不使用辅助预测 p p p。 "Small agents"表示在发现阶段使用更小的智能体网络。 "Without prediction"表示在元学习时不使用学习到的预测 ( y , z ) (y,z) (y,z)。 "Without value"表示在元学习时不使用价值函数 q q q。 "Toy environments"表示用57个网格世界任务（而非Atari游戏）进行元学习。

Analysis（分析）

Qualitative analysis（定性分析）

我们以Disco57为案例（图4），分析了所发现规则的性质。从定性角度看，所发现的预测会在显著事件（如获得奖励或策略熵发生变化）之前出现尖峰（图4a）。我们还通过测量与观测各部分相关的梯度范数，研究了哪些观测特征会引发元学习预测的强烈响应。图4b的结果表明，元学习得到的预测更倾向于关注未来可能相关的物体，而这与策略和价值函数关注的位置不同。这些结果表明，DiscoRL学会了在一个适度的时间视野内识别并预测显著事件，从而对策略和价值函数等现有概念形成了补充。

Information analysis（信息分析）

为验证上述定性结论，我们进一步研究了这些预测中包含了哪些信息。我们首先在10个Atari游戏上收集DiscoRL智能体的数据，并训练一个神经网络，分别从发现的预测、策略或价值函数中预测感兴趣的量。图4c的结果显示，与策略和价值函数相比，所发现的预测包含了更多关于即将到来的大额奖励以及未来策略熵的信息。这表明，所发现的预测可能捕获了策略和价值函数未能充分捕获的、与任务高度相关的独特信息。

Emergence of bootstrapping（自举机制的涌现）

我们还发现了DiscoRL使用自举（bootstrapping）机制的证据。当对元网络在未来时间步的预测输入（ z t + k \mathbf{z}_{t+k} zt+k）进行扰动时，会强烈影响当前时间步的目标 z ^ t \hat{\mathbf{z}}_t z^t（图4d）。这意味着，未来预测被用于构造当前预测的目标。事实证明，这种自举机制以及所发现的预测对性能至关重要（图4e）。如果在计算目标 y ^ \hat{\mathbf{y}} y^ 和 z ^ \hat{\mathbf{z}} z^ 时将元网络的 y \mathbf{y} y 和 z \mathbf{z} z 输入置零（从而阻止自举），性能会显著下降。如果在计算包括策略目标在内的所有目标时都将 y \mathbf{y} y 和 z \mathbf{z} z 输入置零，性能下降得更加严重。这表明，所发现的预测被大量用于指导策略更新，而不仅仅是作为辅助任务存在。

Previous work（相关工作）

人工智能体中的元学习（learning to learn）思想可以追溯到20世纪80年代³⁷，并提出了使用梯度反向传播来训练元学习系统的设想³⁸。使用较慢的元学习过程来元优化较快的学习或适应过程这一核心思想³⁹,⁴⁰，已在迁移学习⁴¹、持续学习⁴²、多任务学习⁴³、超参数优化⁴⁴以及自动化机器学习⁴⁵等众多应用中得到研究。

早期将元学习用于RL智能体的工作包括对信息获取行为的元学习⁴⁶。随后大量工作聚焦于对现有RL算法中的少量超参数进行元学习¹³,¹⁴。这些方法虽取得了一定成效，但难以显著脱离其底层的人工设计算法。另一类工作尝试通过对完全黑箱的算法进行元学习（例如用循环神经网络⁴⁷或突触学习规则⁴⁸实现），以避免引入归纳偏置。尽管在概念上具有吸引力，这些方法却容易对元训练中见过的任务发生过拟合⁴⁹。

使用更广泛类别的预测来表示知识的思想最早出现在时序差分网络⁵⁰中，但当时并未引入元学习机制。类似的思想也曾被用于元学习辅助任务²⁵。我们的工作将这一思想扩展到有效发现智能体所优化的整个损失函数，从而覆盖更广泛的RL规则空间。此外，与以往工作不同，所发现的知识能够泛化到未见过的环境中。

近年来，人们对发现通用RL规则的兴趣不断增长¹,³--⁶,¹⁵。然而，其中大多数工作受限于小规模智能体和简单任务，或发现范围仅限于RL规则的一部分。因此，这些规则很少在具有挑战性的基准上与最先进方法进行全面比较。相比之下，我们在更大的规则空间中进行搜索，其中包括全新的预测形式，并在大量复杂环境中进行发现。因此，我们证明了：有可能发现一种通用RL规则，在具有挑战性的基准上超过多种最先进方法。

Conclusion（结论）

由于具备开放式自我改进的潜力，使机器能够自行发现学习算法被认为是人工智能中最具前景的思想之一。本工作向"由机器设计的RL算法"迈出了一步，这类算法能够在具有挑战性的环境中与、甚至超越一些最优秀的人工设计算法。我们还表明，随着接触到更加多样的环境，所发现的规则会变得更强、也更具泛化性。这表明，未来为高级人工智能设计RL算法的工作，可能将由能够有效利用数据与算力进行扩展的机器来主导。

Online content（在线内容）

所有方法细节、补充参考文献、Nature出版集团的报告摘要、源数据、扩展数据、补充材料、致谢、同行评审信息、作者贡献与利益冲突声明，以及数据与代码可用性说明，均可在 https://doi.org/10.1038/s41586-025-09761-x

查阅。

Methods（方法）

Meta-network（元网络）

元网络将一段智能体输出的轨迹以及来自环境的相关量映射为目标（targets）：

m η : ( f θ ( s t ) , f θ − ( s t ) , a t , r t , b t , ... , f θ ( s t + n ) , f θ − ( s t + n ) , a t + n , r t + n , b t + n ) ↦ ( π ^ t , y ^ t , z ^ t ) m_\eta:\; \big(f_\theta(s_t),\, f_{\theta^-}(s_t),\, a_t,\, r_t,\, b_t,\, \ldots,\, f_\theta(s_{t+n}),\, f_{\theta^-}(s_{t+n}),\, a_{t+n},\, r_{t+n},\, b_{t+n}\big) \;\mapsto\; (\hat{\pi}_t,\hat{\mathbf{y}}_t,\hat{\mathbf{z}}_t) mη:(fθ(st),fθ−(st),at,rt,bt,...,fθ(st+n),fθ−(st+n),at+n,rt+n,bt+n)↦(π^t,y^t,z^t)

其中， η \eta η 表示元参数； f θ = [ π θ ( s ) , y θ ( s ) , z θ ( s ) , q θ ( s ) ] f_\theta=[\pi_\theta(s), \mathbf{y}\theta(s), \mathbf{z}\theta(s), \mathbf{q}_\theta(s)] fθ=[πθ(s),yθ(s),zθ(s),qθ(s)] 是参数为 θ \theta θ 的智能体输出。 a a a、 r r r、 b b b 分别表示智能体采取的动作、奖励以及回合终止指示量。 θ − \theta^- θ− 是参数 θ \theta θ 的指数滑动平均（exponential moving average）。这种函数形式使元网络能够搜索一个严格更大的规则空间，相比之下，元学习一个标量损失函数的搜索空间更小。补充信息（Supplementary Information）中对这一点有进一步讨论。

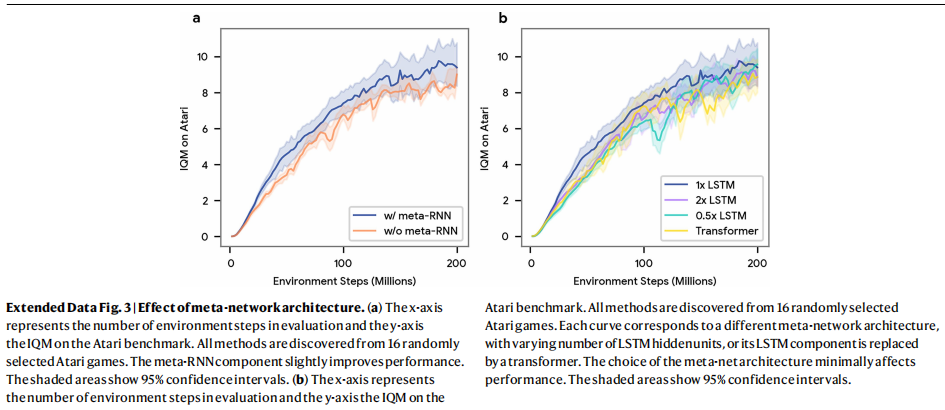
元网络通过沿时间反向展开一个长短期记忆网络（LSTM）来处理这些输入，如图1c所示。这使其能够在生成目标时考虑 n n n步的未来信息，类似于多步RL方法，例如时序差分方法 TD( λ \lambda λ)⁵⁴。我们发现该结构在计算上比transformer等替代方案更高效，同时能达到相近的性能，如扩展数据图3b所示。

在元网络中，与动作相关的输入与输出通过在动作维度上共享权重来处理，并通过在该维度上取平均来计算一个中间嵌入表示。这使元网络能够处理任意数量的动作。更多细节见补充信息。

为了让元网络能够发现更广泛的一类算法（例如奖励归一化），这类算法需要在智能体生命周期内维护统计量，因此我们加入了一个额外的循环神经网络。这个"meta-RNN"是在智能体参数更新的序列上向前展开（从 θ i \theta_i θi到 θ i + 1 \theta_{i+1} θi+1），而不是在单个回合的时间步上展开。 meta-RNN的核心是另一个LSTM模块。对于每一次智能体更新，会将整批轨迹嵌入为一个向量，并将该向量输入这个LSTM。 meta-RNN有可能捕获智能体整个生命周期内的学习动态，从而生成能够适应特定智能体与环境的目标。如扩展数据图3a所示，meta-RNN使总体性能获得了轻微提升。更多细节见补充信息。

Meta-optimization stabilization（元优化的稳定化）

在大规模发现过程中会出现若干挑战，主要原因在于：来自不同环境中智能体的梯度信号不平衡，以及由于智能体生命周期较长而导致的短视梯度问题。我们引入了若干方法来缓解这些问题。

首先，在使用优势行动者--评论家方法估计元梯度中的 ∇ θ J ( θ ) \nabla_\theta J(\theta) ∇θJ(θ) 时，我们对优势项进行如下归一化：

A ˉ = A − μ σ , \bar{A} = \frac{A-\mu}{\sigma}, Aˉ=σA−μ,

其中， A ˉ \bar{A} Aˉ 为归一化后的优势， μ \mu μ 和 σ \sigma σ 分别是智能体整个生命周期内优势值的指数滑动平均与标准差。我们发现，这样做可以使不同环境中的优势项尺度更加均衡。此外，在汇聚来自智能体群体的元梯度时，我们先对每个智能体计算得到的元梯度分别应用一个独立的Adam优化器，然后再对所有智能体的结果取平均：

η ← η + 1 n ∑ i = 1 n A D A M ( g i ) , \eta \leftarrow \eta + \frac{1}{n}\sum_{i=1}^{n}\mathrm{ADAM}(g_i), η←η+n1i=1∑nADAM(gi),

其中， g i g_i gi 表示群体中第 i i i 个智能体的元梯度估计。我们发现，这有助于规范不同智能体产生的元梯度幅度。

我们在元目标 J ( η ) J(\eta) J(η) 中加入两个元正则化损失（ L ent L_{\text{ent}} Lent 和 L KL L_{\text{KL}} LKL），如下所示：

E E E θ [ J ( θ ) − L ent ( θ ) − L KL ( θ ) ] . \mathbb{E}{\mathcal{E}}\mathbb{E}\theta\big[J(\theta) - L_{\text{ent}}(\theta) - L_{\text{KL}}(\theta)\big]. EEEθ[J(θ)−Lent(θ)−LKL(θ)].

其中， L ent ( θ ) = − E s , a [ H ( y θ ( s ) ) + H ( z θ ( s , a ) ) ] L_{\text{ent}}(\theta)=-\mathbb{E}{s,a}[H(\mathbf{y}\theta(s))+H(\mathbf{z}\theta(s,a))] Lent(θ)=−Es,a[H(yθ(s))+H(zθ(s,a))] 是对预测 y \mathbf{y} y 与 z \mathbf{z} z 的熵正则项， H ( ⋅ ) H(\cdot) H(⋅) 表示给定类别分布的熵。我们发现，该正则项有助于防止预测过早收敛。 L KL ( θ ) = D KL ( π θ − ∣ π ^ ) L{\text{KL}}(\theta)=D_{\text{KL}}(\pi_{\theta^-}|\hat{\pi}) LKL(θ)=DKL(πθ−∣π^) 表示目标网络（其参数为智能体参数的指数滑动平均 θ − \theta^- θ−）的策略，与元网络给出的策略目标 π ^ \hat{\pi} π^ 之间的KL散度。该项用于防止元网络提出过于激进、可能导致训练崩溃的更新。

需要强调的是，这些方法仅用于稳定元优化过程，并不决定智能体的更新方式。智能体具体如何更新，仍然完全由元学习得到的规则所决定。

Implementation details（实现细节）

我们开发了一个基于 JAX 库⁵⁵,⁵⁶ 的框架，并借鉴 Podracer 架构⁵⁸，将计算分布到张量处理单元（TPU）⁵⁷ 上。在该框架中，每个智能体都是独立仿真的，所有智能体的元梯度并行计算。元参数通过聚合所有智能体的元梯度，以同步方式进行更新。我们使用 MixFlow-MG⁵⁹ 来降低整体运行的计算成本。

对于 Disco57，我们通过按字典序循环 57 个 Atari 环境，实例化了 128 个智能体。对于 Disco103，我们实例化了 206 个智能体，其中 Atari、ProcGen 和 DMLab-30 中的每个环境各有两份拷贝。 Disco57 的发现过程使用了 1,024 个 TPUv3 核心，运行 64 小时；Disco103 使用了 2,048 个 TPUv3 核心，运行 60 小时。

用于计算元梯度的元价值函数采用 V-Trace³⁴ 进行更新，折扣因子为 0.997，TD( λ \lambda λ) 系数为 0.95。元价值函数与智能体网络均使用 Adam 优化器进行优化，学习率为 0.0003。在元参数更新时，我们使用 Adam 优化器，学习率为 0.001，并进行 1.0 的梯度裁剪。每个智能体的更新基于一个批次的 96 条轨迹，每条轨迹包含 29 个时间步。在每个批次中，在线（on-policy）轨迹与从回放缓冲区采样的轨迹混合，其中回放轨迹占批次的 90%。在每个元步骤中，会生成 48 条轨迹，用于计算元梯度并更新元价值函数。

当某个智能体用完其分配的经验预算后，其参数会被重置。在重置时，会从（2亿、1亿、5000万、2000万）这几类经验预算中重新采样一个新的预算，其采样权重与预算大小成反比，从而保证每一类预算对应的总经验量相同。这一设计基于我们的观察：大量学习发生在生命周期早期；并且在初步的小规模实验中，这种做法带来了边际性能提升。

Hyperparameters and evaluation（超参数与评估）

在对保留基准进行评估时，我们仅在 {0.0001, 0.0003, 0.0005} 中调节学习率。其余超参数均基于文献中的基线算法设定。

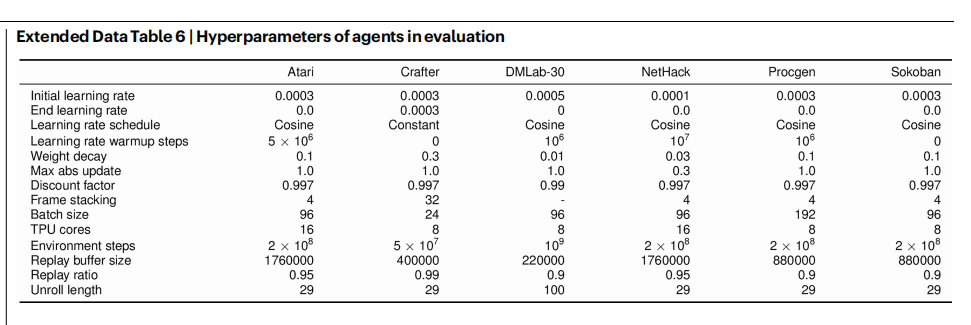
Atari 游戏的评估（图2a 与扩展数据表1）使用了一个参数规模增大的 IMPALA³⁴ 网络，其规模与 MuZero⁸ 所用的智能体网络相匹配。具体而言，我们使用了一个包含 4 个卷积残差块的网络，其滤波器数量分别为 256、384、384 和 256；一个 768 维的共享全连接最终层；以及一个基于 LSTM 的动作条件预测模块，该模块由一个隐藏状态维度为 1,024 的 LSTM 和一个 1,024 维的全连接层组成。 DMLab-30 的评估（图2c 与扩展数据表3）使用了与 IMPALA 相同的动作空间离散化方式和智能体网络结构。超参数列表见扩展数据表6。为验证评估结果的统计显著性，我们在 Atari、ProcGen 和 DMLab 的每个环境上使用两个随机种子，在 Crafter 和 NetHack 上使用三个随机种子，在 Sokoban 上使用五个随机种子。

Analysis details（分析细节）

在图4c的预测分析中，我们训练了多个三层感知机（MLP），每层的隐藏单元数分别为 128、64 和 32。这些 MLP 用于从使用 Disco57 在不同 Atari 游戏上训练得到的智能体输出中，预测诸如未来熵和奖励等量。我们使用了 10 个 Atari 游戏：Alien、Amidar、Battle Zone、Frostbite、Gravitar、Qbert、Riverraid、Road Runner、Robotank 和 Zaxxon。图4c中展示的数值为：未来熵预测的 R 2 R^2 R2 分数，以及通过五折交叉验证得到的大额奖励事件预测准确率。扩展数据图2给出了针对更多预测量的额外分析。对于高维输出（ y , z , z a y, z, z_a y,z,za），我们使用了每层包含 256 个隐藏单元的更大三层 MLP。

Data availability（数据可用性）

本文所呈现的结果未使用任何外部数据。

Code availability（代码可用性）

我们以开源许可证的形式在 https://github.com/google-deepmind/disco_rl

提供元训练与评估代码，并附带 Disco103 的元参数。文中所使用的所有基准均为公开可用。

Acknowledgements（致谢）

我们感谢相关作者在思想讨论、工程基础设施支持、高层次反馈以及早期版本评阅等方面所提供的帮助。

Author contributions（作者贡献）

J.O.、I.K.、G.F. 和 D.A.C. 贡献相同；其余作者分别在方法开发、分析、工程实现、评估、论文撰写和项目指导中承担不同角色。

Competing interests（利益冲突）

针对本文所述工作的部分内容，相关专利申请已提交并处于审理阶段；Google LLC 对该工作拥有所有权及潜在商业利益。

Additional information（附加信息）

补充材料可在 https://doi.org/10.1038/s41586-025-09761-x 查阅。通信与材料请求请联系 Junhyuk Oh 或 David Silver。 Nature 感谢 Kenji Doya、Joel Lehman 及其他匿名审稿人对本文同行评审的贡献。重印与许可信息见 http://www.nature.com/reprints。