一、线性回归
1.线性回归算法
线性回归是利用数理统计种回归分析,来确定或两种以上变量间相互依赖的定量关系的一种统计分析方法。
数据规律呈现线性关系。简单来说,我们就要找出那条线,当然,实际问题中所有点是不可能全部落在直线上,所以我们求到的直线是点到它的距离最小。
2.线性回归模型介绍
1)一元线性模型
现在有一个案例,自变量为工资,因变量为贷款额度
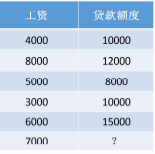 工资影响贷款额度。
工资影响贷款额度。
根据上面我们搭建一个一元线性回归模型: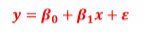
这里的β0和β1是模型的参数,后面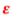 是误差项,它不属于直线的表达式,也就是说,β1是直线斜率,β0是截距。
是误差项,它不属于直线的表达式,也就是说,β1是直线斜率,β0是截距。
2)多元线性模型
上面是只有一个自变量,下面我们建造多元模型: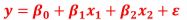
和一元线性是一个道理
3)误差项分析
误差项不能省略,是一定会产生的,当这条直线是所有点到直线距离都比较小的那条直线,这时候误差项满足高斯分布,也就是这里的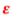 满足高斯分布,又称正态分布。
满足高斯分布,又称正态分布。
关于对误差项分析涉及到数学公式和式子化简,这里就不论述
经过数学方法后会得到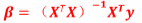 ,能够求得β得最小值
,能够求得β得最小值
4)相关系数:变量之间是否有关
数学中我们也学过,这个是用来研究和度量变量间相关性,一般用r表示


5)拟合优度
直线拟合是否是最优的?使用判定系数R^2


3.线性回归实例
1)一元线性回归,会用到sklearn库
数据,预测广告投入的销售额

代码实现
python
import pandas as pd
from sklearn.linear_model import LinearRegression
#导入数据
data=pd.read_csv('data.csv',encoding='utf-8',engine='python')
#打印相关系数矩阵
corr=data[['广告投入','销售额']].corr()
#估计模型参数,建立回归模型
lr_model=LinearRegression()#回归模型
x=data[['广告投入']]#分为数据x和标签y
y=data[['销售额']]
lr_model.fit(x,y)#训练
#对回归模型进行检验
'''
score在这的用处:调整R方,判断自变量对因变量的解释程度
R方越接近1,自变量对因变量的解释就越好
F检验:方程整体显著性检验
T检验:方程系数显著性检验
score给的是R方'''
score=lr_model.score(x,y)
print(score)
#利用回归模型进行预测
print(lr_model.predict([[29]]))
print(lr_model.predict([[25],[31]]))
'''a:自变量,b:截距'''
a=lr_model.coef_
b=lr_model.intercept_
# print(a,b,type(a),type(b))
print('线性回归模型为:y={:.2f}x+{:.2f}'.format(a[0][0],b[0]))
2)多元线性回归1
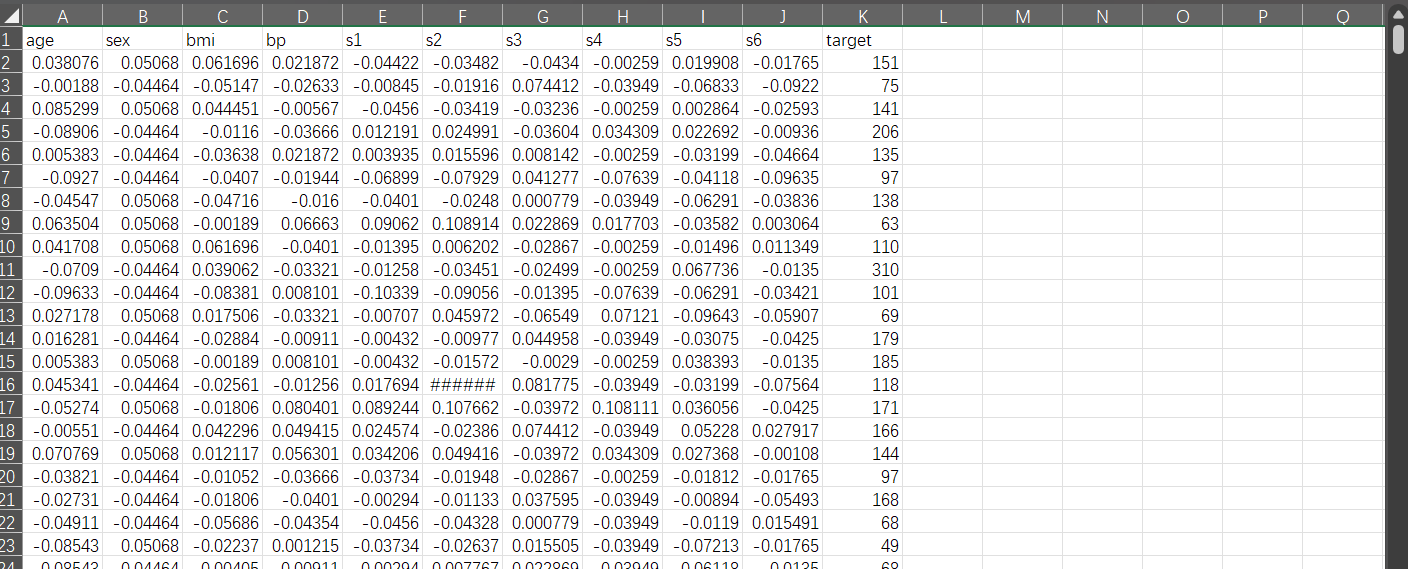
数据400多条:预测糖尿病
分别为年龄,性别,bmi值,bp值,......target为糖尿病指标值
python
import pandas as pd
from sklearn.linear_model import LinearRegression
#导入数据
data=pd.read_csv('糖尿病数据.csv',encoding='utf-8',engine='python')
#打印相关系数矩阵
corr=data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6','target']].corr()
#估计模型参数,建立回归模型
lr_model=LinearRegression()
x=data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6']]
y=data[['target']]
lr_model.fit(x,y)
#对回归模型进行检验
score=lr_model.score(x,y)
#利用回归模型进行预测
print(lr_model.predict([['0.038075906','0.050680119','0.061696207','0.021872355','-0.044223498',
'-0.034820763','-0.043400846','-0.002592262','0.019908421','-0.017646125']]))
a=lr_model.coef_#系数
b=lr_model.intercept_#截距
# print(a,b,type(a),type(b))
print('线性回归模型为:y={:.2f}x0+{:.2f}x1+{:.2f}x2+{:.2f}x3+{:.2f}x4+{:.2f}x5+'
'{:.2f}x6+{:.2f}x7+{:.2f}x8+{:.2f}x9+{:.2f}'.format(a[0][0],a[0][1],a[0][2],a[0][3]
,a[0][4],a[0][5],a[0][6],a[0][7],a[0][8],a[0][9],b[0]))
该数据预测误差很大,这涉及很多个方面。
4.总结
无论多元还是一元,方法都是一样的
二、逻辑回归
1.逻辑回归介绍
是分类算法,如果把线性回归看作离所有点最近的一条直线,那逻辑回归就是一条直线,把类别不同的的数据点在其上的投影对应的区域分开
分类有两种,二分类和多分类
2.二分类
数据分为两类,一类打上标签1,一类打上标签0,因为模型判断类别时只能输出数值,判断出是1类就会输出1,是0类就输出0
例如一条直线,方程为y=α1xx+α2 ,如下图我们有两种数据,输出y值,人眼很容易看出是两类,机器怎么分辨,如果给一个新数据要去预测属于哪一类,机器又该怎么判断
所以虽然是二分类,但是我们要利用空间直角坐标系,再引出一个维度Y,
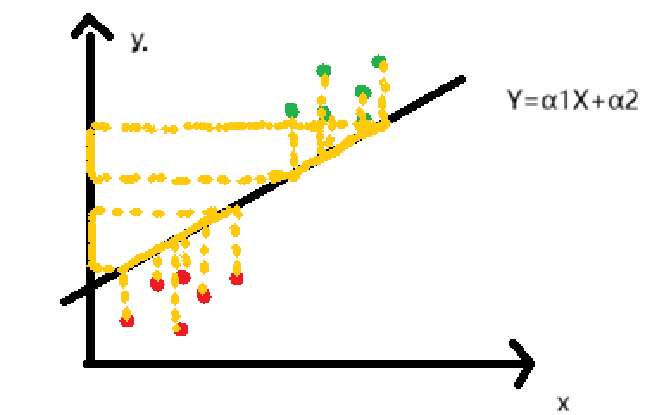
下面加入一个维度,也引进一个函数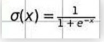
这个函数图像是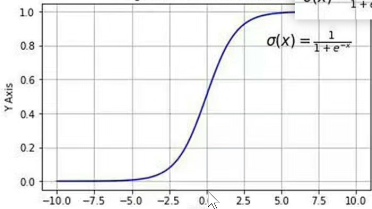
这里的x就是我们图上的y
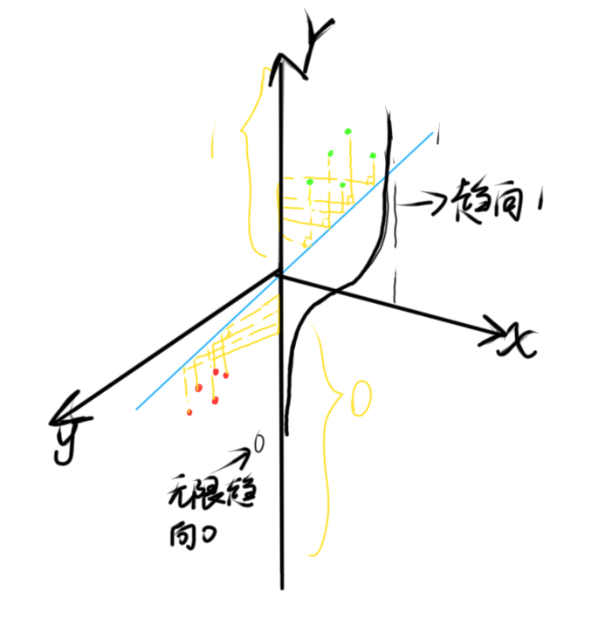
就是这么一个数学过程

3.具体例子
上述只是我们理解的过程,我们主要要对代码实现
银行贷款例子
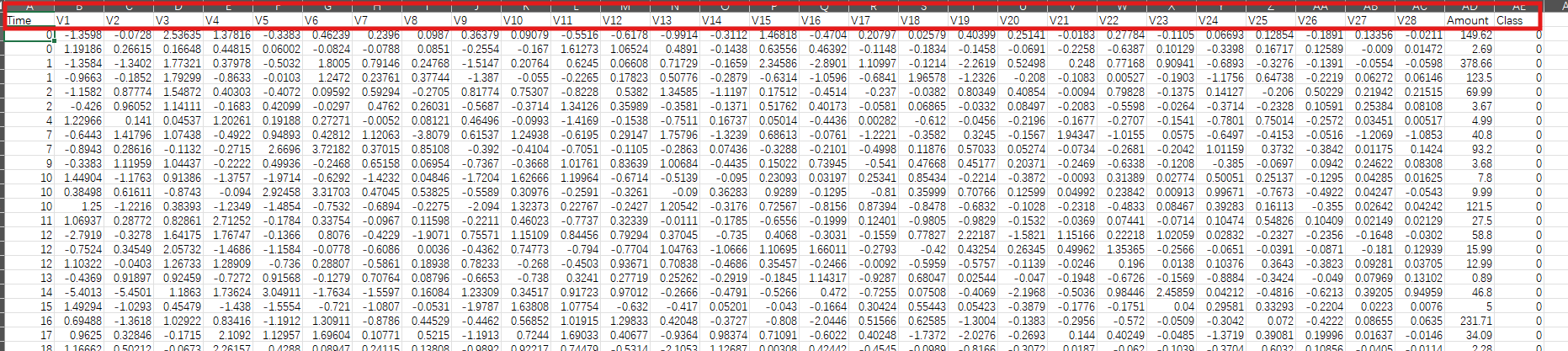
下面是我们的数据,银行根据用户信息进行判断是否要贷款给用户,0是同意贷款,1是不同意贷款,这里数据有上万条,没展示完全,任务就是训练让其能进行预测是否贷款给用户
另外我们这里的数据是经过z标准化处理过的,由数值有正有负可以看出,其中有Amount列没有标准化,Time是用户登记的时间,一般银行进行业务的窗口不止有一个,所以时间有一样的,这里Time并没有什么用,前面都是数据,最后target就是最后结果。
我们绘图时原则上是不支持出现中文的,但是在这里我们导入sklearn中的metrics就可以画图的时候出现中文了
python
import pandas as pd
from sklearn.preprocessing import scale
import matplotlib.pyplot as plt
from pylab import mpl
from sklearn.model_selection import train_test_split#专门用来对数据集进行切分的函数
from sklearn.linear_model import LogisticRegression#逻辑回归的类,所有的算法都封装再这个类里面
from sklearn import metrics
'''整理我们进行逻辑回归的数据'''
data=pd.read_csv(r"E:\filedata\creditcard.csv")#读取文件
# print(data.head)#输出前五行的数据,检测文件是否被读取
data['Amount']=pd.DataFrame(scale(data['Amount']))#把Amount列也进行标准化
data=data.drop(['Time'],axis=1)#用不到的Time列删去
'''绘制图型前要准备的'''
mpl.rcParams['font.sans-serif']=['Microsoft YaHei']
mpl.rcParams['axes.unicode_minus']=False#选择表格上中文的格式
value_count=pd.value_counts(data['Class'])#统计各类别的个数
print(value_count,type(value_count))#输出各类别个数
'''绘制图形'''
plt.title('正负例样本数')#标题
plt.xlabel('类别')#x轴标签
plt.ylabel('频数')#y轴标签
value_count.plot(kind='bar')#设置图像类型为bar,条形图
plt.show()#显示数据分布
'''建立模型处理数据'''
X_data=data.drop('Class',axis=1)
Y_data=data.Class
'''对数据集进行划分'''
x_train,x_test,y_train,y_test=train_test_split(X_data,Y_data,test_size=0.3,random_state=1000)
#这里对数据的划分,0.3的意思是百分之三十作为测试集,这数据不是按照文件按顺序分配的,
#而是随机抽取的,并且我们这里还用到了种子,
#也就是说随机抽取的数据抽取后是训练集那后面就一直是训练集,是预测值就一直是预测值
lr=LogisticRegression(C=0.01)#关于这里的C参数,我们会放到后面去讲,现在只需要用着这个参数
lr.fit(x_train,y_train)#训练
'''测试集预测结果'''
testpre=lr.predict(x_test)#预测
complete=lr.score(x_test,y_test)#预测准确率
print(testpre,complete)
'''获取分类结果报告'''
print(metrics.classification_report(y_test,testpre))输出:
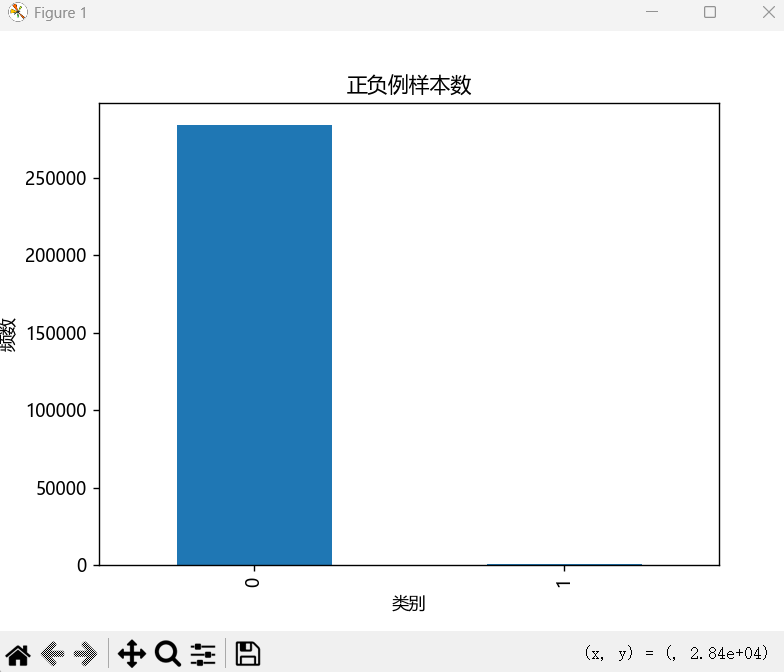
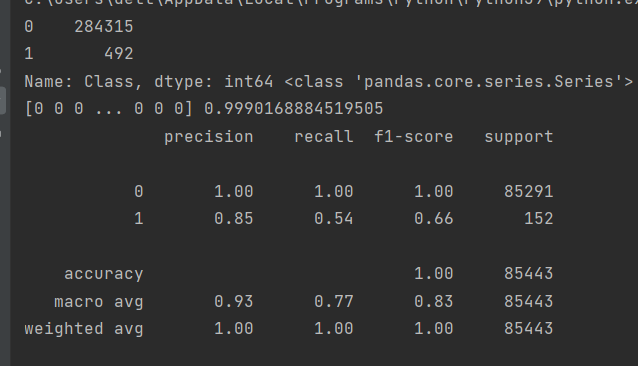
4.关于上述代码获取分类报告
分析上述输出结果,第一个输出是对各类型的个数进行统计并绘图,由图可以看出我们的类型之间数量差距是很大的,正确率也达到了百分之99点多
正确率那么高虽看着很好但其实很误导人,这个模型是不能拿去使用的
首先我们训练数据中,0类和1类数量差距很大,这也会让训练后的模型不准确,基本上输出全为0,计算正确率时由于0类比较多,准确率也会很高。这会牵扯到召回率和精确率这两个含义。
例如假设要对15个人预测是否患病,使用1表示患病,0表示正常,预测结果如下:

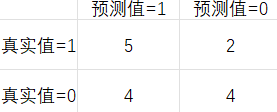
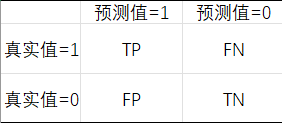
TP(True Positive):5 FP(False Positive):4
FN(False Negative):2 TN(True Negative):4
1)准确率:预测值与真实值一致的情况
accuracy(准确率)=(TP+TN)/(TP+TN+FP+FN)
2)召回率:从真实值出发
recall=TP/(TP+FN)
3)精确率:预测值中有多少被预测正确了
precision=TP/(TP+FP)
4)F1值(score)
F1=2*(precision*recall)/(precision+recall)
5)特异率
specificity=TN/(TN+FP)
我们所做的模型几乎都是要运用于现实中的,现实中就要本着"宁可错杀也不放过一个"的原则。预测人是否生病,没生病人就不会进一步检查,要是被模型预测出生病,至少他们会去医院进行检查再次确认。所以就算有一点可能我们的模型都不能判定人没病,银行系统和医疗系统是一个道理,都想尽可能的分辨出有异常的,,也就是比较关注召回率。
所以我们可以打印出分类结果报告查看召回率。
5.C=0.01中C是什么?
在上述代码中有一处参数C=0.01
这里的参数会涉及到模型的拟合程度,模型的拟合程度分为两种:
1)欠拟合
模型没有训练好
2)过拟合
模型再训练集中表现良好,但是在测试集上就不行了,原因是在训练集上为了追求好的效果,包括损失大小,准确率高......模型参数太过于复杂
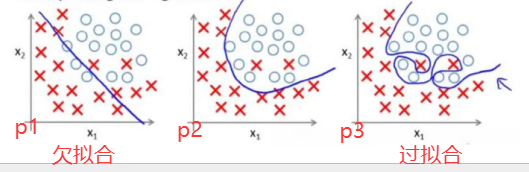
p2就是比较正常的情况我们允许有一些异常数据
欠拟合的模型可以多进行训练,关键是过拟合的模型存在的问题该怎么解决,是需要我们思考的
用来解决过拟合,我们可以使用正则化惩罚,而这里的参数C就是控制正则化惩罚程度的关键参数
6.正则化惩罚
会存在我们输入数据时,有两种或多种权重值满足拟合的要求
也就是说,输入x=[1,1,1,1]
权重1:w1=[1,0,0,0]对应式子为y=1*x1+0*x2+0*x3+0*x4
权重2:w2=[0.25,0.25,0.25,0.25]对应式子为y=0.25*x1+0.25*x2+0.25*x3+0.25*x4
带入后两个式子值是一样的,那到底该选择哪个?
下面式子是线性回归/逻辑回归的损失函数,后面加上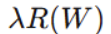 的就是正则化惩罚项
的就是正则化惩罚项
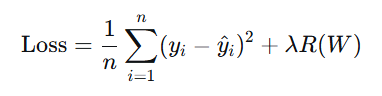
正则化惩罚的功能:主要用于惩罚权重参数w,一般有L1和L2正则化
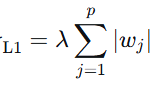
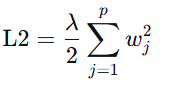
w1带入L1:为1(先把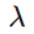 放一边)
放一边)
w2带入L1:为1,所以从L1中比较不出w1和w2哪个比较好
w1带入L2:为1(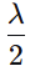 先放一边)
先放一边)
w2带入L2:为4*(0.25)^2=1/4
损失函数损失越小越好,所以我们这里选择w2
选择的标准其实就是,w1权重,有三个零,这样无论未知数为多少,都为0,只有x1自己发挥作用,而w2中权重分布比较均匀,每个未知数值都能发挥其值的作用。