强化学习第四课 —— 深度强化学习：Policy Gradient 入门

编辑

引言

一、回顾：基于价值的方法

[1.1 核心思想](#1.1 核心思想)

[1.2 局限性](#1.2 局限性)

二、为何要直接优化策略？

[2.1 Policy Gradient 的核心思想](#2.1 Policy Gradient 的核心思想)

[2.2 直接优化策略的优势](#2.2 直接优化策略的优势)

[三、Policy Gradient 定理](#三、Policy Gradient 定理)

[3.1 推导过程](#3.1 推导过程)

[3.2 最终形式](#3.2 最终形式)

[四、REINFORCE 算法](#四、REINFORCE 算法)

[4.1 算法流程](#4.1 算法流程)

[4.2 代码示例](#4.2 代码示例)

[五、降低方差：Baseline 的引入](#五、降低方差：Baseline 的引入)

[5.1 Baseline 技巧](#5.1 Baseline 技巧)

[5.2 最佳 Baseline](#5.2 最佳 Baseline)

[六、从 REINFORCE 到现代算法](#六、从 REINFORCE 到现代算法)

七、总结

引言

在强化学习（Reinforcement Learning）的世界里，我们的目标是让智能体（Agent）学会在环境中做出最优决策。实现这一目标主要有两大流派：基于价值（Value-Based） 的方法和 基于策略（Policy-Based） 的方法。今天，我们要深入探讨的是后者的核心技术------Policy Gradient（策略梯度）。

你可能会问：既然 Q-Learning 和 DQN 这类基于价值的方法已经很强大了，为什么我们还需要直接优化策略呢？这正是本文要回答的核心问题！

一、回顾：基于价值的方法

在深入 Policy Gradient 之前，让我们先简单回顾一下基于价值的方法是如何工作的。

1.1 核心思想

基于价值的方法（如 Q-Learning、DQN）的核心是学习一个价值函数：

状态价值函数 V(s)：表示在状态 s 下，遵循某策略能获得的期望累积奖励
动作价值函数 Q(s, a)：表示在状态 s 下采取动作 a，然后遵循某策略能获得的期望累积奖励

一旦学到了准确的 Q 函数，策略就隐式地确定了：

简单来说，就是选择 Q 值最大的动作。

1.2 局限性

这种方法虽然优雅，但存在几个关键问题：

问题一：只能处理离散动作空间

当动作空间是连续的（比如机器人关节的角度、汽车的油门/方向盘控制），对所有可能的动作取 argmax 是不现实的。想象一下，你要在无限多个连续值中找最大值！

问题二：策略是确定性的

基于 Q 函数导出的策略是确定性的------同一状态下永远选择同一动作。但在很多场景下，随机策略才是最优的，比如：

石头剪刀布游戏（确定性策略必输）
部分可观测环境
需要探索的场景

问题三：价值函数的微小变化可能导致策略剧变

Q 值的微小扰动可能改变 argmax 的结果，导致策略突然跳变，这使得学习过程不够稳定。

二、为何要直接优化策略？

现在，让我们正式回答这个核心问题！💡

2.1 Policy Gradient 的核心思想

与其绕道价值函数，不如直接对策略进行参数化，然后通过梯度上升来优化它！

我们用表示一个由参数定义的策略，它输出在状态 s 下采取动作 a 的概率。我们的目标是找到最优的，使得期望累积奖励最大化：

其中是一条轨迹（trajectory），是这条轨迹的总奖励。

2.2 直接优化策略的优势

优势一：天然支持连续动作空间

策略网络可以直接输出连续动作的分布参数（比如高斯分布的均值和方差），从中采样即可得到动作。再也不用对无限个动作算 argmax 了！

复制代码

# 伪代码示例
mean, std = policy_network(state)
action = Normal(mean, std).sample()

优势二：可以学习随机策略

策略直接输出动作的概率分布，天然支持随机性。这在对抗性环境、需要探索、或部分可观测场景下至关重要。

优势三：更好的收敛性质

策略参数的小变化只会导致策略分布的小变化，使得优化过程更加平滑稳定。

优势四：端到端优化

我们直接优化我们真正关心的目标------累积奖励，而不是间接地通过价值函数。

三、Policy Gradient 定理

好了，理念很美好，但如何计算对的梯度呢？毕竟期望是对轨迹分布求的，而轨迹分布本身就依赖于！🤔

这就是 Policy Gradient 定理 大显身手的地方。

3.1 推导过程

让我们一步步来推导这个关键结果。

首先，目标函数可以写成：

对求梯度：

这里有个技巧，使用对数导数技巧（Log-Derivative Trick）：

代入得：

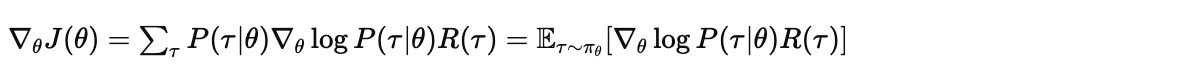
接下来，展开：

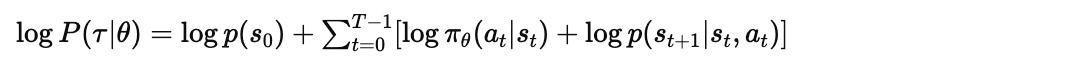
关键观察：和是环境动态，与无关！

因此：

3.2 最终形式

Policy Gradient 定理：

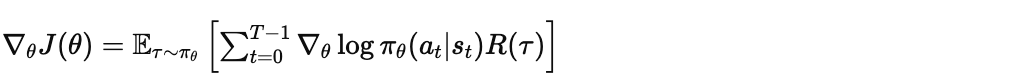
这个结果太美了！✨ 我们不需要知道环境的动态模型，只需要：

用当前策略采样轨迹
计算每个动作的
用轨迹奖励加权

四、REINFORCE 算法

基于 Policy Gradient 定理，我们可以得到最基础的策略梯度算法------REINFORCE。

4.1 算法流程

复制代码

REINFORCE 算法
================
1. 初始化策略参数 θ
2. 重复以下步骤：
   a. 用策略 π_θ 采样一条轨迹 τ = (s_0, a_0, r_0, s_1, a_1, r_1, ...)
   b. 计算轨迹总奖励 R(τ) = Σ_t γ^t r_t
   c. 计算梯度估计：g = Σ_t ∇_θ log π_θ(a_t|s_t) · R(τ)
   d. 更新参数：θ ← θ + α · g

4.2 代码示例

下面是一个简化的 PyTorch 实现：

复制代码

import torch
import torch.nn as nn
import torch.optim as optim
from torch.distributions import Categorical

class PolicyNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=128):
        super().__init__()
        self.network = nn.Sequential(
            nn.Linear(state_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, hidden_dim),
            nn.ReLU(),
            nn.Linear(hidden_dim, action_dim),
            nn.Softmax(dim=-1)
        )
    
    def forward(self, state):
        return self.network(state)
    
    def select_action(self, state):
        probs = self.forward(state)
        dist = Categorical(probs)
        action = dist.sample()
        log_prob = dist.log_prob(action)
        return action.item(), log_prob

def reinforce(env, policy, optimizer, num_episodes=1000, gamma=0.99):
    for episode in range(num_episodes):
        state = env.reset()
        log_probs = []
        rewards = []
        
        # 采样一条轨迹
        done = False
        while not done:
            state_tensor = torch.FloatTensor(state)
            action, log_prob = policy.select_action(state_tensor)
            next_state, reward, done, _ = env.step(action)
            
            log_probs.append(log_prob)
            rewards.append(reward)
            state = next_state
        
        # 计算折扣累积奖励
        returns = []
        G = 0
        for r in reversed(rewards):
            G = r + gamma * G
            returns.insert(0, G)
        returns = torch.tensor(returns)
        
        # 标准化 (可选但推荐)
        returns = (returns - returns.mean()) / (returns.std() + 1e-8)
        
        # 计算损失并更新
        policy_loss = []
        for log_prob, G in zip(log_probs, returns):
            policy_loss.append(-log_prob * G)
        
        optimizer.zero_grad()
        loss = torch.stack(policy_loss).sum()
        loss.backward()
        optimizer.step()

五、降低方差：Baseline 的引入

REINFORCE 虽然简单，但有个大问题------方差太大！😰

由于我们用蒙特卡洛采样来估计梯度，每条轨迹的奖励波动会导致梯度估计的高方差，进而使学习过程非常不稳定。

5.1 Baseline 技巧

一个关键的洞察是：我们可以从奖励中减去一个不依赖于动作的 baseline ，而不改变梯度的期望：

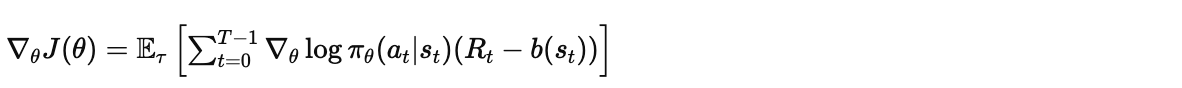
为什么这不会引入偏差？因为：

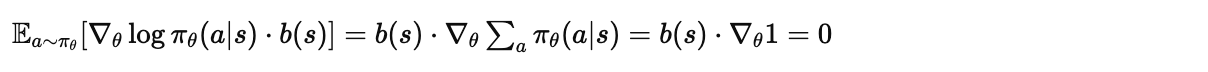
5.2 最佳 Baseline

理论上，最优的 baseline 是什么呢？

可以证明，当（状态价值函数）时，方差最小。此时：

这就是 Advantage（优势函数）！它衡量的是某个动作相比平均水平好多少。

这就引出了著名的 Actor-Critic 架构：

Actor ：策略网络，负责选动作
Critic ：价值网络，负责评估状态价值，作为 baseline

六、从 REINFORCE 到现代算法

REINFORCE 只是起点。现代策略梯度算法在此基础上做了大量改进：

算法	主要改进
Actor-Critic (A2C)	引入 Critic 降低方差，使用 TD 误差
A3C	异步并行训练多个 Actor
TRPO	通过信任域约束保证策略更新的稳定性
PPO	用 Clip 机制简化 TRPO，效果好且实现简单
SAC	最大熵框架，鼓励探索，适合连续控制

其中 PPO（Proximal Policy Optimization） 可能是目前应用最广泛的算法，包括 ChatGPT 的 RLHF 训练中就使用了 PPO！

七、总结

让我们回顾一下今天学到的核心要点：

为何直接优化策略：
- 支持连续动作空间
- 能学习随机策略
- 更稳定的优化过程
- 端到端优化真正的目标
Policy Gradient 定理：提供了一种不需要环境模型就能估计策略梯度的方法
REINFORCE：最基础的策略梯度算法，简单但方差大
Baseline/Advantage：通过引入 baseline 降低方差，Actor-Critic 架构由此诞生

策略梯度方法打开了强化学习的新大门，让我们能够处理更复杂、更真实的问题。希望这篇文章能帮助你建立对 Policy Gradient 的直觉理解！

如果你觉得这篇文章有帮助，欢迎分享给更多对强化学习感兴趣的朋友！有任何问题，欢迎在评论区讨论。 🌟