摘要------3GPP 提出的 5G 定位技术为公共安全、车载系统和基于位置的服务等应用开启了新的可能性。然而,这些应用要求精确且可靠的定位性能,这促使了更新的定位技术的提出。为了进一步推进对这些技术的研究,在本文中,我们开发了一个符合 3GPP 标准的 5G 定位测试平台,该平台包含了 gNodeBs (gNBs) 和用户设备 (UE)。该测试平台利用 gNB 发送的新无线电 (NR) 定位参考信号 (PRS) 在 UE 端生成到达时间 (TOA) 估计值。我们在数学上建立了影响 TOA 估计值的 gNB 间和 UE-gNB 间的时间偏差模型,并检验了它们对定位性能的影响。此外,我们提出了一种用于估计这些时间偏差的校准方法。进一步地,我们研究了环境对 TOA 估计值的影响。我们的发现基于我们的数学模型,并得到了实验结果的支持。
CCS 概念
- 网络 → \rightarrow → 网络实验;
- 硬件 → \rightarrow → 硬件验证。
文章目录
-
- [1 Introduction](#1 Introduction)
- [2 5G DL-TDOA PRS Specications](#2 5G DL-TDOA PRS Specications)
-
- [2.1 5G-Positioning Architecture](#2.1 5G-Positioning Architecture)
- [2.2 PRS Frame Structure and Conguration](#2.2 PRS Frame Structure and Conguration)
- [3 5G Positioning Testbed Overview](#3 5G Positioning Testbed Overview)
- [4 Mathematical Model of 5G Testbed](#4 Mathematical Model of 5G Testbed)
1 Introduction
随着近年来支持第五代 (5G) 蜂窝网络的物联网 (IoT) 设备快速增加,对 5G 定位的兴趣也同步增长,因为其具有将精确位置服务与通信无缝集成的潜力。基于 5G 蜂窝网络的定位有潜力为各种应用提供定位服务,因为手机无处不在。一些应用包括公共安全 [2, 5]、车载定位 [8]、医疗保健 [17] 和资产追踪 [11]。
鉴于其应用的多样性,5G 定位提出了独特的挑战。例如,
在诸如消防等公共安全场景中,需要提高垂直轴定位精度(verticalaxis positioning accuracy) [7]。车载定位性能在城市场景中会受到不利影响。
随着对定位性能需求的不断增加,我们注意到一个主要的成因是环境效应,例如无线链路为视距 (LOS) 的概率以及各种多径效应 [9]。此外,诸如基于衍射的定位(diraction-based positioning) [4] 等新技术已被提出,并在理论定位性能方面显示出显著的改进。将此类技术应用到现实世界需要对理论结果进行实验验证。尽管一些研究已经对 5G 定位测试平台进行了实验评估 [3, 14, 15],但仍需要对时间同步模型(time synchronization models)进行更全面的验证,并对硬件、软件和环境相关的实施挑战进行调查。
在我们的研究中,我们通过提供一个符合 3GPP 标准的 5G 定位测试平台来填补这些空白,该平台使用软件定义无线电(Software Defined Radios,SDR)和名为 OpenAirInterface (OpenAirInterface,OAI) 的开源蜂窝软件构建,具有促进在现实场景中加速测试和部署先进定位算法的潜力。我们提出的解决方案依赖于数学建模的使用,随后是实验结果。主要贡献概述如下。
-
符合 3GPP 标准的定位测试平台的开发: 使用各种硬件和软件组件,我们模拟 5G gNB 和 UE,以基于使用 5G 下行链路 PRS 提取 TOA 测量值来实现 2D 定位能力。
-
多径对定位的影响: 基于室外和室内实验,我们研究了多径对 TOA 估计的影响,这最终会影响定位性能。我们强调了基于使用诸如 延迟扩展 (delay spread) 等指标来表征信号传播环境,从而选择合适信号带宽的作用。
-
解决时间同步误差: 尽管在我们的测试平台中采用了基于硬件的时间同步程序,但 gNB 无法实现完美的 gNB 间时间同步。我们在数学上对这些残留的 gNB 间时序误差进行建模,论证了它们对定位的影响,然后提出了一种校准程序(calibration procedure)来估计这些偏差,从而使测试平台符合 3GPP 标准。我们进行了进一步的实验,以验证由校准程序得出的估计时序偏差的时间稳定性和有效性。
2 5G DL-TDOA PRS Specications
2.1 5G-Positioning Architecture
系统架构(见图 1)由 5G UE、下一代 (Next Generation,NG) 无线接入网 (Radio Access Network,RAN) 和 5G 核心网 (5G Core Network,CN) 组成。
-
NG RAN 由能够与 5G CN 通信的演进型 LTE eNodeB (eNB) 和完全的 5G gNB 组成。
- Fully 5G gNB (完全的 5G gNB),通常理解的 "真 5G 基站",用 5G NR (New Radio) 空口技术与手机通信
- Evolved LTE eNodeB (演进型 LTE eNB),"升级版的 4G 基站",使用 LTE 信号与手机通信),但它具备了与 5G 核心网 (5G CN) 对话的能力。
-
5G CN 包含接入和移动性管理功能 (Access Mobility Function,AMF) 和位置管理功能 (Location Management Function,LMF)。
- AMF 通过管理 5G UE 的连接和移动性来维持连续的通信和位置更新。
- LMF 通过 AMF 从 NG-RAN 接收必要的定位服务请求,包括用于定位的测量值和关于 UE 的信息 [16]。
LMF 依靠 AMF 作为中介,从无线接入网(基站)获取计算位置所需的原材料(测量数据和设备信息)。
商用 5G 网络通常使用 5G UE,这些 UE 使用 5G NR 空口 (NR-Uu) 与 5G gNB 通信。我们的研究使用 5G gNB 通过 NR-Uu 向 UE 发送下行链路 NR PRS 信号,以进行位置估计。这种 5G 定位架构支持利用到达时间差 (TDOA) 来确定 UE 位置的方法。
2.2 PRS Frame Structure and Conguration
我们的定位系统专注于利用从三个 gNB 发送到单个 UE 的 DL PRS 信号,以便在 UE 处进行 TOA 测量。PRS 是一种具有交错资源元素 (RE) 模式的宽带信号,提供极好的自相关和低互相关特性。这些特性使其特别适合精确的定位应用。[1] 中的 TS 38.211 提供了有关生成 PRS 参考信号序列方法的详细信息。
PRS 可以灵活配置以映射到 5G 帧结构上,粒度可低至符号级别。这种灵活性允许根据部署要求在时域和频域中映射 PRS。具有更大子载波间隔的更高参数集 (numerology) 提供了增强的时间分辨率和降低的延迟,使其成为城市环境中精确定位的理想选择。每个 5G 帧的长度为 10 ms 10 \text{ ms} 10 ms,并分为 10 10 10 个子帧。根据所使用的参数集,每个子帧可以包含一个或多个时隙。在我们的案例中,我们采用参数集 1 1 1,具有 30 kHz 30 \text{ kHz} 30 kHz 子载波间隔 (scs) 和 106 106 106 个物理资源块 (Physical Resource Blocks,PRB),每个 PRB 在频域中包含 12 12 12 个子载波,每个 0.5 ms 0.5 \text{ ms} 0.5 ms 的时隙包含 14 14 14 个符号,产生的总带宽为 106 × 12 × 30 kHz = 38.16 MHz 106 \times 12 \times 30 \text{ kHz} = 38.16 \text{ MHz} 106×12×30 kHz=38.16 MHz。
每个 gNB 都可以配置其独有的下行 (DL) PRS 传输参数。UE 通过接收这些 PRS 信号来估算到达时间 (TOA)。具体的 PRS 配置参数定义如下:
-
PRS 资源集周期 (PRS Resource Set Period) :
定义了 PRS 信号发送的循环周期(以时隙为单位)。简单来说,就是每隔多少个时隙,这套信号会重新发送一次。
-
PRS 资源偏移 (PRS Resource Offset) :
定义了每个 PRS 资源在周期内的起始位置。它决定了信号具体是从哪一个时隙开始传输的。
-
PRS 资源重复 (PRS Resource Repetition) :
表示重复因子。它规定了在一个 PRS 资源集周期内,该 PRS 资源需要重复发送多少次(即占用多少个时隙)。
-
PRS 资源时间间隔 (PRS Resource Time Gap) :
定义了两次连续重复发送之间的间隔 。如果设置了重复发送(即重复因子 > 1 >1 >1),该参数决定了相邻两次重复传输之间相隔多少个时隙。
图 2 提供了 PRS 配置的图解表示,其中包括 20 20 20 个时隙的 PRS 资源集周期 和 2 2 2 个时隙的 PRS 资源集偏移 ,分别为 gNB1、gNB2 和 gNB3 设置的 1 1 1、 2 2 2 和 3 3 3 个时隙的 PRS 资源偏移 ,每个 PRS 资源的 PRS 资源重复 为 1 1 1,以及 1 1 1 个时隙的 PRS 资源时间间隔。
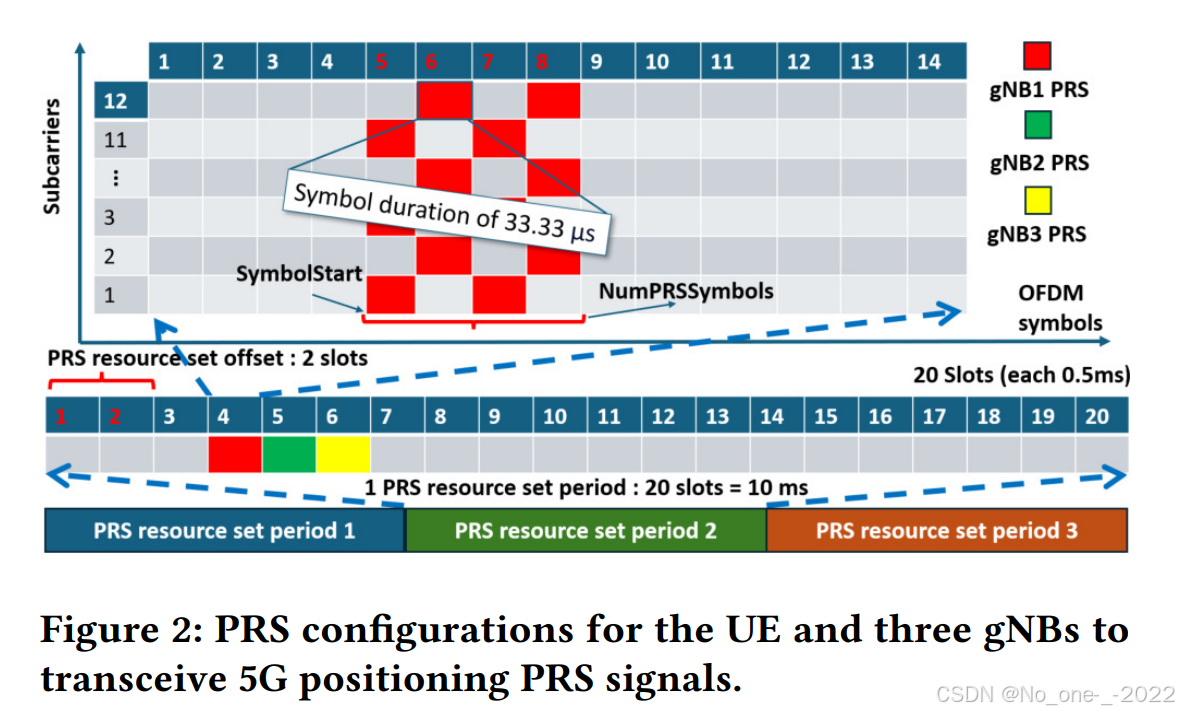
最终位置 = PRS 资源集偏移 (PRS Resource Set Offset) + PRS 资源偏移 (PRS Resource Offset) + 1 ( 因为图是从1开始数的 ) 最终位置 = \text{PRS 资源集偏移 (PRS Resource Set Offset)} + \text{PRS 资源偏移 (PRS Resource Offset)} + 1 (\text{因为图是从1开始数的}) 最终位置=PRS 资源集偏移 (PRS Resource Set Offset)+PRS 资源偏移 (PRS Resource Offset)+1(因为图是从1开始数的)
这些配置确保来自不同 gNB 的 PRS 被映射到唯一的时隙,从而防止它们之间的信号重叠。上述配置侧重于时隙级配置。我们现在关注频域和时隙内符号的配置。在每个时隙内,连续的正交频分复用 (OFDM) 符号的数量是为每个 PRS 资源专门分配的。此方面的 PRS 配置参数为:(1) 起始符号 (Symbol Start) ,(2) OFDM 符号数量 (Number of OFDM Symbols) ,(3) RB 偏移 (RB Offset) ,(4) RB 数量 (Number of RBs) ,以及 (5) 梳齿大小 (Comb Size)。有关这些参数的详细信息可以在 [1] 中找到。
3 5G Positioning Testbed Overview
本节描述了利用软件定义无线电 (SDR) 和 OpenAirInterface (OAI) 蜂窝软件协议栈构建我们 5G 定位测试平台原型的过程。以此设置作为参考,我们研究了精确估计 UE 的 2D 位置所面临的挑战,并探索了解决这些问题的初步缓解技术。
如图 3 所示,我们的定位测试平台由四个设备组成。每个设备包含一台 SDR B210 和一台台式计算机。每台 B210 都连接到 Octoclock-G,用于时间和频率同步。Octoclock 配备了 GPS 驯服振荡器(GPS-disciplined oscillator),用于在 50 ns 50 \text{ ns} 50 ns 内实现设备间的时间同步。使用 Octoclock 实现的设备振荡器的频率稳定性为 20 parts-per-billion (ppb) 20 \text{ parts-per-billion (ppb)} 20 parts-per-billion (ppb) [10]。
在每个设备中,计算机运行着开源的、符合 3GPP 标准的 5G PHY 层软件协议栈 ------ OAI [12],并且每个设备都可以配置为作为 UE 或 gNB 运行。我们将其中一个设备配置为 UE,而将其余三个设备配置为 gNB。我们将在建立系统的数学模型之后,在 5.1 节中对测试平台进行进一步的讨论。
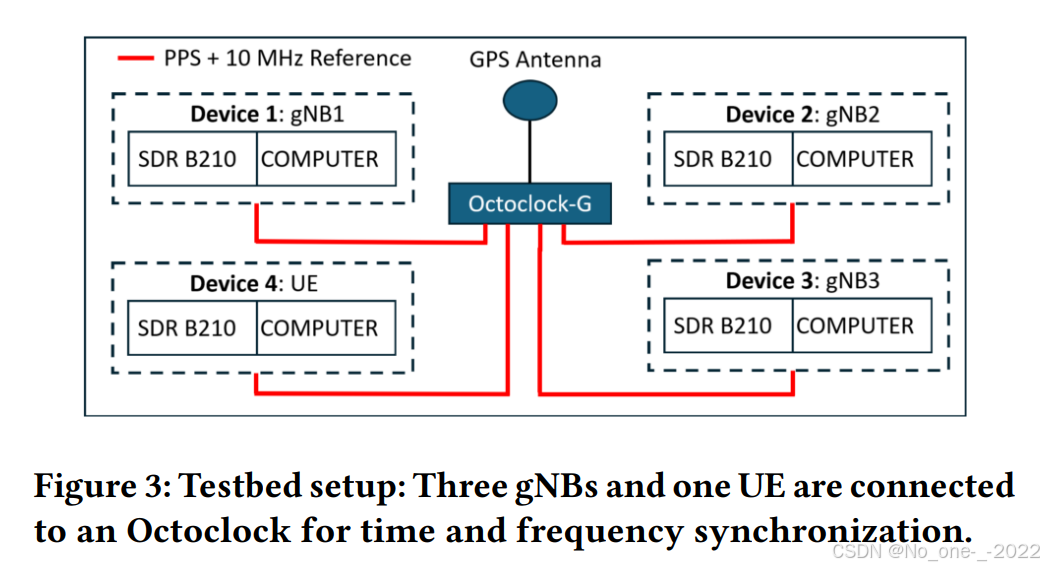
- GPS 接收机通常会输出两个用于同步的信号:一个是 10 MHz Reference(参考时钟,管频率/速度),另一个就是 PPS(秒脉冲,管相位/时间点)。
4 Mathematical Model of 5G Testbed
在 3GPP 5G 标准中,假设 UE 相对于 gNB 具有未知的时钟偏差,而所有 gNB 被认为是完美同步的。然而,在我们的 5G 测试平台中,尽管进行了硬件同步,设备之间仍然存在残留的未知时间偏差,正如 Octoclock 规格说明书 [10] 中所述,如图 4 所示。在本节中,我们将为这些偏差建立数学模型,并演示如何从信道估计中提取 TOA 信息。然后,我们描述了一个校准过程来实现 gNB 的同步,而 UE 保持一个未知的固定时间偏差,该偏差可以使用标准的 TDOA 技术 [18] 与其位置进行联合估计。
我们假设 UE 位于 α i = [ x n i , y n i ] T \boldsymbol{\alpha}i = [x{n_i}, y_{n_i}]^T αi=[xni,yni]T,第 j j j 个 gNB 位于 [ x a j , y a j ] T [x_{a_j}, y_{a_j}]^T [xaj,yaj]T。总共有三个 gNB,即 j ∈ { 1 , 2 , 3 } j \in \{1, 2, 3\} j∈{1,2,3}。因此,第 j j j 个 gNB 与第 i i i 个 UE 位置之间的欧几里得距离 p j ( α i ) p_j(\boldsymbol{\alpha}_i) pj(αi) 可以表示为
p j ( α i ) = ( x a j − x n i ) 2 + ( y a j − y n i ) 2 . (1) p_j(\boldsymbol{\alpha}i) = \sqrt{(x{a_j} - x_{n_i})^2 + (y_{a_j} - y_{n_i})^2}. \tag{1} pj(αi)=(xaj−xni)2+(yaj−yni)2 .(1)
对于第 j j j 个 gNB,沿第一条到达路径的信号传播时间为 p j ( α i ) c \frac{p_j(\boldsymbol{\alpha}_i)}{c} cpj(αi),其中 c c c 为光速。现在,在 UE 处进行的 TOA 测量可以表示为
τ i , j = p j ( α i ) c + ϕ + Δ j + n i , j (2) \tau_{i,j} = \frac{p_j(\boldsymbol{\alpha}i)}{c} + \phi + \Delta_j + n{i,j} \tag{2} τi,j=cpj(αi)+ϕ+Δj+ni,j(2)
这里, τ i , j \tau_{i,j} τi,j 是第 j j j 个 gNB 与第 i i i 个 UE 位置之间的 TOA 估计值, ϕ \phi ϕ 是 gNB-UE 时间偏差。假设 j = 1 j=1 j=1 为参考 gNB,我们有 gNB 间的时间偏差 Δ 2 \Delta_2 Δ2 和 Δ 3 \Delta_3 Δ3 作为相对于参考 gNB 的未知时间偏差。注意,根据定义,我们有 Δ 1 = 0 \Delta_1 = 0 Δ1=0。来自第 j j j 个 gNB 的 UE 处的测量噪声为 n j n_j nj,并且被认为是零均值高斯噪声,且在不同 gNB 之间是独立的。