前言
学习机器学习的过程中,我逐渐意识到:
如果只有代码,而没有理论,就很难真正理解模型在做什么
如果只有概念,而缺少一个系统框架,又难以把知识串成体系
《统计学习方法》正好提供了这样一个结构清晰的入口------它把机器学习的核心思想和经典算法用统计学的语言表达出来,帮助我们理解算法背后的原理。

因此,我决定开启这个专栏,用自己的方式整理学习笔记。主要目标是:
- 用更直白的语言梳理书中的概念
- 把知识点整理成便于查阅和复习的形式
- 记录自己的理解和思考过程
这些笔记主要是我个人的学习记录,如果恰好对你也有帮助,那就更好了。希望通过这个过程,能让自己对机器学习的理论基础有更扎实的理解。
第7章------支持向量机(下)
SVM下篇深入探讨非线性问题的解决方案,通过核技巧将低维空间映射到高维特征空间,介绍正定核的性质和常用核函数(如多项式核、高斯核),最后详细阐述SMO(序列最小最优化)算法。
7.3 非线性支持向量机与核函数
要想搞清楚非线性支持向量机,那么我们首先先快速回顾一下线性支持向量机的特点有哪些。
在线性支持向量机中,包括线性可分和线性不可分两种情况,思路都是用一个"分离超平面"进行划分。对于线性不可分的情况,我们引入"松弛变量",得到对应特殊点的判断条件,从而解决线性支持向量机的分类问题。
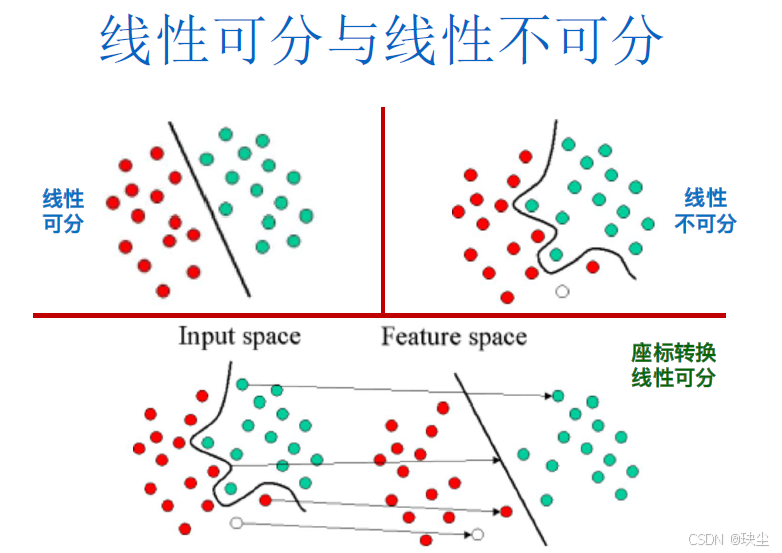
同理,对于非线性的支持向量机,自然也有非线性可分和非线性不可分两种情况。我们先来看"非线性可分支持向量机":通过超曲面可以将输入数据完全分开。比如说,想象一个椭圆形的分界线,在椭圆内部的都是红点,在椭圆外部的都是紫点。这就是个典型的非线性可分的图形。
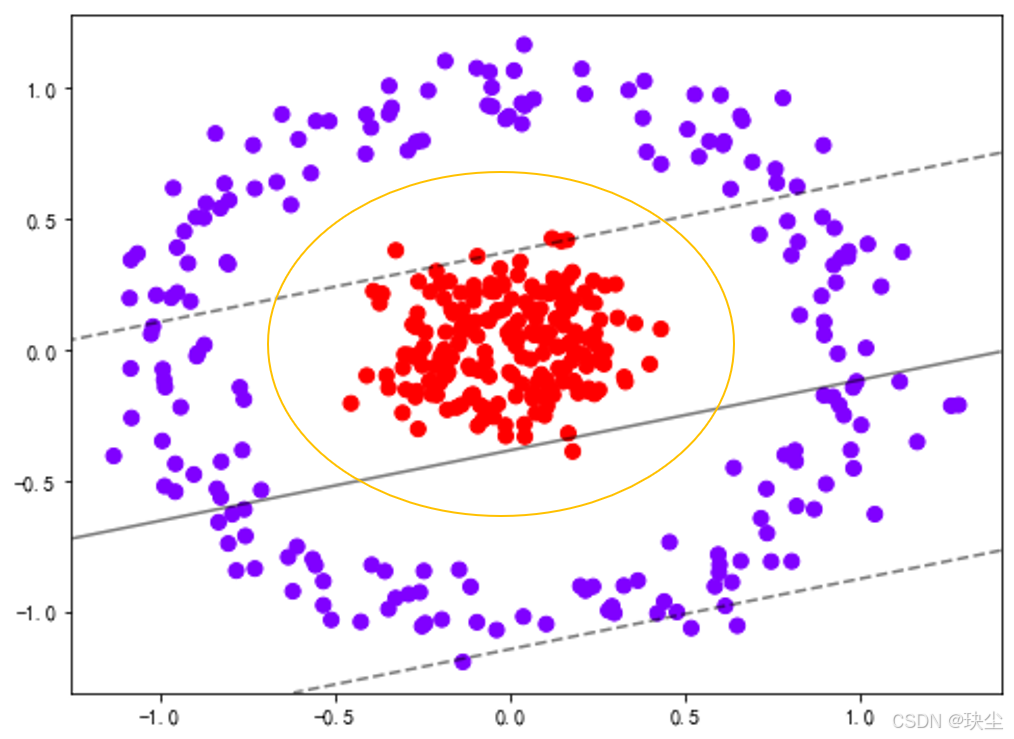
此时,分离两类数据的就不再是一条直线或者一个平面了,而是一个弯曲的曲线或曲面,在这里我们统称为"超曲面"。
搞清楚了这个思路,我们就可以看看如何用线性问题来解决这种非线性问题了。
其实核心想法很巧妙:既然在原来的空间里数据是非线性可分的,那我们能不能把数据映射到一个更高维的空间里,让它在那个高维空间里变成线性可分的呢?就好比你在二维平面上看到的是一个复杂的曲线,但如果你把它放到三维空间里去看,可能就变成了一个简单的平面分界了。
这样一来,我们就可以继续使用之前学过的线性支持向量机的方法来解决问题。但这里有个关键点:我们并不需要真的去计算这个高维空间的具体映射,而是通过"核函数"来巧妙地替代内积计算,这就是核技巧的精髓所在。
7.3.1 核技巧
核技巧应用到支持向量机,其基本想法就是通过一个非线性变换将输入空间对应到一个特征空间,使得在输入空间中的超曲面模型对应于特征空间中的超平面模型。这样,分类问题就可以通过在特征空间中求解线性支持向量机来完成。
但这里有个关键问题:如果我们真的去计算这个高维映射 ϕ(x)\phi(x)ϕ(x),计算量会非常大,特别是当特征空间维度很高甚至无穷维时,这几乎是不可行的。
这就是核函数的巧妙之处。我们回顾一下线性支持向量机的对偶问题,会发现无论是目标函数还是决策函数,都只涉及输入实例与实例之间的内积 xi⋅xjx_i \cdot x_jxi⋅xj。如果我们用映射后的内积 ϕ(xi)⋅ϕ(xj)\phi(x_i) \cdot \phi(x_j)ϕ(xi)⋅ϕ(xj) 来替换原来的内积,就得到了非线性支持向量机。
关键在于,我们定义一个核函数 K(x,z)=ϕ(x)⋅ϕ(z)K(x, z) = \phi(x) \cdot \phi(z)K(x,z)=ϕ(x)⋅ϕ(z),它直接计算两个向量在高维空间中的内积,而不需要先把 xxx 和 zzz 映射到高维空间再做内积。这样就避免了显式计算高维映射的麻烦。
具体来说,在对偶问题的目标函数中,原来的内积 xi⋅xjx_i \cdot x_jxi⋅xj 被核函数 K(xi,xj)K(x_i, x_j)K(xi,xj) 替代;在决策函数中,内积同样被核函数替代。最终我们得到的分类决策函数是:
f(x)=sign(∑i=1Nsαi∗yiK(xi,x)+b∗)f(x) = \text{sign}\left(\sum_{i=1}^{N_s}\alpha_i^* y_i K(x_i, x) + b^*\right)f(x)=sign(i=1∑Nsαi∗yiK(xi,x)+b∗)
这就是核技巧的本质:学习是隐式地在特征空间进行的,不需要显式地定义特征空间和映射函数。我们只需要选择合适的核函数,就能巧妙地利用线性分类学习方法与核函数解决非线性问题。当映射函数是非线性函数时,学习到的含有核函数的支持向量机就是非线性分类模型。
7.3.2 正定核
前面我们说可以通过核函数 K(x,z)=ϕ(x)⋅ϕ(z)K(x, z) = \phi(x) \cdot \phi(z)K(x,z)=ϕ(x)⋅ϕ(z) 来避免显式计算高维映射,但这里有个问题:我们怎么知道一个给定的函数 K(x,z)K(x, z)K(x,z) 是不是真的对应着某个映射呢?换句话说,什么样的函数才能作为核函数使用?
这就是正定核要解决的问题。通常所说的核函数就是正定核函数(positive definite kernel function)。判断一个函数是否为正定核,关键看它对应的Gram矩阵是否半正定。
正定核的充要条件
设 K:X×X→RK: \mathcal{X} \times \mathcal{X} \to \mathbf{R}K:X×X→R 是对称函数,则 K(x,z)K(x, z)K(x,z) 为正定核函数的充要条件是对任意 xi∈Xx_i \in \mathcal{X}xi∈X,i=1,2,⋯ ,mi = 1, 2, \cdots, mi=1,2,⋯,m,K(x,z)K(x, z)K(x,z) 对应的Gram矩阵
K=[K(xi,xj)]m×mK = [K(x_i, x_j)]_{m \times m}K=[K(xi,xj)]m×m
是半正定矩阵。
这个定理给出了判断正定核的实用标准。但在实际应用中,我们通常直接使用已经被证明是正定核的常用核函数,而不需要每次都去验证Gram矩阵。根据Mercer定理,正定核比Mercer核更具一般性。
正定核的等价定义
设 X⊂Rn\mathcal{X} \subset \mathbf{R}^nX⊂Rn,K(x,z)K(x, z)K(x,z) 是定义在 X×X\mathcal{X} \times \mathcal{X}X×X 上的对称函数,如果对任意 xi∈Xx_i \in \mathcal{X}xi∈X,i=1,2,⋯ ,mi = 1, 2, \cdots, mi=1,2,⋯,m,K(x,z)K(x, z)K(x,z) 对应的Gram矩阵 K=[K(xi,xj)]m×mK = [K(x_i, x_j)]_{m \times m}K=[K(xi,xj)]m×m 是半正定矩阵,则称 K(x,z)K(x, z)K(x,z) 是正定核。
7.3.3 常用核函数
在实际应用中,我们通常从几种常用的核函数中选择。下面介绍三种最常用的核函数。
1. 多项式核函数(polynomial kernel function)
K(x,z)=(x⋅z+1)pK(x, z) = (x \cdot z + 1)^pK(x,z)=(x⋅z+1)p
其中 ppp 是多项式的次数。这个核函数对应的支持向量机是一个 ppp 次多项式分类器,分类决策函数成为
f(x)=sign(∑i=1Nsαi∗yi(xi⋅x+1)p+b∗)f(x) = \text{sign}\left(\sum_{i=1}^{N_s}\alpha_i^* y_i(x_i \cdot x + 1)^p + b^*\right)f(x)=sign(i=1∑Nsαi∗yi(xi⋅x+1)p+b∗)
2. 高斯核函数(Gaussian kernel function)
K(x,z)=exp(−∥x−z∥22σ2)K(x, z) = \exp\left(-\frac{\|x - z\|^2}{2\sigma^2}\right)K(x,z)=exp(−2σ2∥x−z∥2)
对应的支持向量机是高斯径向基函数(radial basis function)分类器,分类决策函数成为
f(x)=sign(∑i=1Nsαi∗yiexp(−∥x−xi∥22σ2)+b∗)f(x) = \text{sign}\left(\sum_{i=1}^{N_s}\alpha_i^* y_i \exp\left(-\frac{\|x - x_i\|^2}{2\sigma^2}\right) + b^*\right)f(x)=sign(i=1∑Nsαi∗yiexp(−2σ2∥x−xi∥2)+b∗)
高斯核是应用最广泛的核函数之一,参数 σ\sigmaσ 控制了函数的"宽度"。
3. 字符串核函数(string kernel function)
核函数不仅可以定义在欧氏空间上,还可以定义在离散数据的集合上。字符串核就是定义在字符串集合上的核函数,在文本分类、信息检索、生物信息学等领域都有应用。
字符串核函数的基本思想是:通过映射 ϕn(s)\phi_n(s)ϕn(s) 将字符串 sss 映射到特征空间 Hn=RΣn\mathcal{H}_n = R^{\Sigma^n}Hn=RΣn。两个字符串 sss 和 ttt 上的字符串核函数是基于映射 ϕn\phi_nϕn 的特征空间中的内积:
kn(s,t)=∑u∈Σn[ϕn(s)]u[ϕn(t)]u=∑u∈Σn∑(i,j):s(i)=t(j)=uλl(i)λl(j)k_n(s, t) = \sum_{u \in \Sigma^n}[\phi_n(s)]u[\phi_n(t)]u = \sum{u \in \Sigma^n}\sum{(i,j): s(i)=t(j)=u}\lambda^{l(i)}\lambda^{l(j)}kn(s,t)=u∈Σn∑[ϕn(s)]u[ϕn(t)]u=u∈Σn∑(i,j):s(i)=t(j)=u∑λl(i)λl(j)
其中,0<λ⩽10 < \lambda \leqslant 10<λ⩽1 是一个衰减参数,l(i)l(i)l(i) 表示字符串 iii 的长度。字符串核函数给出了字符串 sss 和 ttt 中长度等于 nnn 的所有子串组成的特征向量的余弦相似度。直观上,两个字符串相同的子串越多,它们就越相似,字符串核函数的值就越大。字符串核函数可以由动态规划快速地计算。
7.3.4 非线性支持向量分类机
前面我们已经理解了核技巧的精髓:通过核函数避免显式计算高维映射。现在我们来看看如何把这个思想真正应用到非线性分类问题中。
回顾一下线性支持向量机,我们求解的对偶问题和最终的决策函数都只涉及样本之间的内积 xi⋅xjx_i \cdot x_jxi⋅xj。那么要扩展到非线性情况,思路就很自然了:把所有的内积 xi⋅xjx_i \cdot x_jxi⋅xj 替换成核函数 K(xi,xj)K(x_i, x_j)K(xi,xj) 就可以了。
具体来说,原来线性支持向量机的对偶问题是优化 ∑∑αiαjyiyj(xi⋅xj)\sum\sum\alpha_i\alpha_j y_i y_j (x_i \cdot x_j)∑∑αiαjyiyj(xi⋅xj),现在变成优化 ∑∑αiαjyiyjK(xi,xj)\sum\sum\alpha_i\alpha_j y_i y_j K(x_i, x_j)∑∑αiαjyiyjK(xi,xj)。
原来的决策函数是 f(x)=sign(∑αi∗yi(xi⋅x)+b∗)f(x) = \text{sign}(\sum\alpha_i^* y_i (x_i \cdot x) + b^*)f(x)=sign(∑αi∗yi(xi⋅x)+b∗),现在变成 f(x)=sign(∑αi∗yiK(xi,x)+b∗)f(x) = \text{sign}(\sum\alpha_i^* y_i K(x_i, x) + b^*)f(x)=sign(∑αi∗yiK(xi,x)+b∗)。
就这么简单!我们不需要知道数据被映射到了什么样的高维空间,也不需要知道具体的映射函数是什么。只要选定一个核函数,比如高斯核或多项式核,就能自动地在高维空间中进行分类。
这就是非线性支持向量机的完整流程:
首先,根据问题特点选择合适的核函数。比如数据分布比较复杂时可以选择高斯核,如果想要多项式决策边界可以选择多项式核。
然后,设定惩罚参数 CCC,求解带核函数的对偶问题,得到最优解 α∗\alpha^*α∗。
接着,用 α∗\alpha^*α∗ 计算偏置项 b∗b^*b∗,最终得到分类决策函数 f(x)=sign(∑i=1Nαi∗yiK(x,xi)+b∗)f(x) = \text{sign}(\sum_{i=1}^{N}\alpha_i^* y_i K(x, x_i) + b^*)f(x)=sign(i=1∑Nαi∗yiK(x,xi)+b∗)
这个决策函数看起来和线性支持向量机很相似,但实际上已经是一个复杂的非线性分类器了。核函数的选择直接决定了模型的表达能力和泛化性能,实际应用中通常需要通过交叉验证等方法来选择最合适的核函数及其参数。
7.4 序列最小最优化算法
支持向量机在理论上是一个凸二次规划问题,这意味着解是全局最优的,看起来很理想。但问题在于,当训练样本很多时,直接用通用的二次规划算法求解,会变得又慢又耗资源,几乎无法实际使用。因此,关键不在"能不能解",而在"怎么解得快"。
正是在这样的背景下,Platt 在 1998 年提出了序列最小最优化(SMO) 算法。它不是去正面硬解整个大问题,而是换了一个非常聪明的思路:既然一次优化所有变量太难,那就每次只动最少的变量。
SMO 的核心想法可以一句话概括:每次只优化两个拉格朗日乘子,其余的全部固定。这样一来,原本规模很大的优化问题,就被拆成了一个又一个非常小的子问题。更重要的是,这种"只含两个变量"的子问题,可以直接写出解析解,不需要复杂的数值计算,这让算法整体变得非常高效。
为什么选择两个变量而不是一个?
这是因为支持向量机的约束条件 ∑αiyi=0\sum\alpha_i y_i = 0∑αiyi=0。如果固定其他所有变量,只更新一个变量 αi\alpha_iαi,那这个变量的值实际上是被其他变量完全确定的,没有优化的空间。但如果同时更新两个变量 α1\alpha_1α1 和 α2\alpha_2α2,就有了优化的自由度。
SMO 的整体运行方式就是不断重复这样一个过程:选出一对变量,固定其他所有变量,快速算出这两个变量的最优更新值;然后再换下一对变量继续做。只要不断迭代,最终所有变量都会满足 KKT 条件,算法就自然收敛了。
7.4.1 两个变量二次规划的求解方法
当我们选定要更新的两个变量 a1a_1a1 和 a2a_2a2时,其余变量都被当作常数。此时,原问题会退化成一个只有两个变量的二次优化问题。由于约束条件的存在,a1a_1a1 和 a2a_2a2 的取值并不是随意的,而是必须落在一条直线上;再结合 0≤ai≤𝐶0 ≤ a_i ≤ 𝐶0≤ai≤C 这样的盒约束,最终可行解就是这条直线上的一段线段。
因此,问题就变成了:在这条线段上,找到目标函数的最低点 。实际做法是先忽略边界限制,算出一个"理论上最优"的 α2\alpha_2α2,再把它强行压回到允许的区间 [L,H][L, H][L,H] 里,这个过程叫"剪辑"。
无约束更新公式是
α2new,unc=α2old+y2(E1−E2)η\alpha_2^{\text{new,unc}} = \alpha_2^{\text{old}} + \frac{y_2(E_1 - E_2)}{\eta}α2new,unc=α2old+ηy2(E1−E2)
这里的 EiE_iEi 表示模型在样本 xix_ixi 上的预测误差,而 η\etaη 可以理解为两个样本在特征空间中的"差异程度"。直观上,误差差得越多,这次更新就越大。
得到新的 α2\alpha_2α2 之后,α1\alpha_1α1 可以通过约束关系自动算出来,因此这一步几乎不需要额外计算。
7.4.2 变量的选择方法
SMO 算法跑得快不快,很大程度上就看每一轮选哪两个变量来更新。变量选得好,参数改动大、收敛就快;选得不好,来回折腾,效率就低。
第 1 个变量的选择(外层循环)
第一个变量的原则很直观:优先找"最不守规矩"的样本,也就是违反 KKT 条件最严重的点。
实际做法是:
先重点检查那些位于间隔边界上的支持向量(满足 0<αi<C0<\alpha_i<C0<αi<C 的样本)。这些点对模型最关键,如果它们都已经满足 KKT 条件,说明模型已经比较稳定了;
如果还有不满足的,就优先从这里选第一个变量;
只有当这些边界上的点都没问题时,才去遍历整个训练集。
第 2 个变量的选择(内层循环)
当第一个变量 α1\alpha_1α1 已经确定后,第二个变量 α2\alpha_2α2 的目标只有一个:让这次更新"改得尽量多"。
从更新公式可以看出,α2\alpha_2α2 的变化大小主要由 ∣E1−E2∣|E_1 - E_2|∣E1−E2∣ 决定。这个差值越大,α2\alpha_2α2 更新得就越狠,模型进展也越快。
所以常用的启发式策略是:
- 如果 E1E_1E1 是正的,就去找 误差最小 的那个样本当作 α2\alpha_2α2;
- 如果 E1E_1E1 是负的,就去找 误差最大 的那个样本当作 α2\alpha_2α2。
本质上就是:让两个样本的预测误差"拉得越开越好"。
为了加快查找速度,算法会把所有样本的误差 EiE_iEi 都存到一个列表里,随用随取。
如果按照上面的规则选出来的 α2\alpha_2α2 并没有让目标函数明显下降,那就说明这对变量"不太合适"。这时就换一种方式:
- 先在间隔边界上的支持向量中挨个尝试;
- 如果还是不行,再退一步,遍历整个训练集,直到找到一个能让目标函数下降的 α2\alpha_2α2。
每一轮成功更新完两个变量后,都要同步更新阈值 bbb ,并重新计算相关样本的误差 EiE_iEi。
这样做是为了保证下一轮变量选择和更新时,使用的都是最新、准确的信息。
7.4.3 SMO算法
SMO算法
输入 :训练数据集 T={(x1,y1),(x2,y2),⋯ ,(xN,yN)}T = \{(x_1, y_1), (x_2, y_2), \cdots, (x_N, y_N)\}T={(x1,y1),(x2,y2),⋯,(xN,yN)},其中 xi∈X=Rnx_i \in \mathcal{X} = \mathbf{R}^nxi∈X=Rn,yi∈Y={−1,+1}y_i \in \mathcal{Y} = \{-1, +1\}yi∈Y={−1,+1},i=1,2,⋯ ,Ni = 1, 2, \cdots, Ni=1,2,⋯,N,精度 ε\varepsilonε;
输出 :近似解 α^\hat{\alpha}α^。
(1) 取初值 α(0)=0\alpha^{(0)} = 0α(0)=0,令 k=0k = 0k=0;
(2) 选取优化变量 α1(k)\alpha_1^{(k)}α1(k),α2(k)\alpha_2^{(k)}α2(k),解析求解两个变量的最优化问题,求得最优解 α1(k+1)\alpha_1^{(k+1)}α1(k+1),α2(k+1)\alpha_2^{(k+1)}α2(k+1),更新 α\alphaα 为 α(k+1)\alpha^{(k+1)}α(k+1);
(3) 若在精度 ε\varepsilonε 范围内满足停机条件(所有样本满足KKT条件),则转 (4);否则令 k=k+1k = k + 1k=k+1,转 (2);
(4) 取 α^=α(k+1)\hat{\alpha} = \alpha^{(k+1)}α^=α(k+1)。
本章概要
1. 支持向量机最简单的情况是线性可分支持向量机,或硬间隔支持向量机。构建它的条件是训练数据线性可分。其学习策略是最大间隔法。 可以表示为凸二次规划问题,其原始最优化问题为
minw,b12∥w∥2\min_{w,b} \frac{1}{2}\|w\|^2w,bmin21∥w∥2
s.t. yi(w⋅xi+b)−1⩾0,i=1,2,⋯ ,N\text{s.t. } y_i(w \cdot x_i + b) - 1 \geqslant 0, \quad i = 1,2,\cdots,Ns.t. yi(w⋅xi+b)−1⩾0,i=1,2,⋯,N
求得最优化问题的解为 w∗w^*w∗,b∗b^*b∗,得到线性可分支持向量机,分离超平面是:
w∗⋅x+b∗=0w^* \cdot x + b^* = 0w∗⋅x+b∗=0
分类决策函数是:
f(x)=sign(w∗⋅x+b∗)f(x) = \text{sign}(w^* \cdot x + b^*)f(x)=sign(w∗⋅x+b∗)
最大间隔法中,函数间隔与几何间隔是重要的概念。
线性可分支持向量机的最优解存在且唯一。位于间隔边界上的实例点为支持向量。最优分离超平面由支持向量完全决定。
二次规划问题的对偶问题是:
minα12∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi\min_{\alpha} \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_j y_i y_j(x_i \cdot x_j) - \sum_{i=1}^{N}\alpha_iαmin21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαi
s.t. ∑i=1Nαiyi=0\text{s.t. } \sum_{i=1}^{N}\alpha_i y_i = 0s.t. i=1∑Nαiyi=0
αi⩾0,i=1,2,⋯ ,N\alpha_i \geqslant 0, \quad i = 1,2,\cdots,Nαi⩾0,i=1,2,⋯,N
通常,通过求解对偶问题学习线性可分支持向量机,即首先求解对偶问题的最优值 α∗\alpha^*α∗,然后求最优值 w∗w^*w∗ 和 b∗b^*b∗,得出分离超平面和分类决策函数。
2. 现实中训练数据是线性可分的情形较少,训练数据往往是近似线性可分的,这时使用线性支持向量机,或软间隔支持向量机。线性支持向量机是最基本的支持向量机。
对于噪声或例外,通过引入松弛变量 ξi\xi_iξi,使其"可分",得到线性支持向量机学习的凸二次规划问题,其原始最优化问题是:
minw,b,ξ12∥w∥2+C∑i=1Nξi\min_{w,b,\xi} \frac{1}{2}\|w\|^2 + C\sum_{i=1}^{N}\xi_iw,b,ξmin21∥w∥2+Ci=1∑Nξi
s.t. yi(w⋅xi+b)⩾1−ξi,i=1,2,⋯ ,N\text{s.t. } y_i(w \cdot x_i + b) \geqslant 1 - \xi_i, \quad i = 1,2,\cdots,Ns.t. yi(w⋅xi+b)⩾1−ξi,i=1,2,⋯,N
ξi⩾0,i=1,2,⋯ ,N\xi_i \geqslant 0, \quad i = 1,2,\cdots,Nξi⩾0,i=1,2,⋯,N
求解原始最优化问题的解 w∗w^*w∗,b∗b^*b∗,得到线性支持向量机,其分离超平面为
w∗⋅x+b∗=0w^* \cdot x + b^* = 0w∗⋅x+b∗=0
分类决策函数为:
f(x)=sign(w∗⋅x+b∗)f(x) = \text{sign}(w^* \cdot x + b^*)f(x)=sign(w∗⋅x+b∗)
线性支持向量机的解 w∗w^*w∗ 唯一但 b∗b^*b∗ 不一定唯一。
对偶问题是:
minα12∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi\min_{\alpha} \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_j y_i y_j(x_i \cdot x_j) - \sum_{i=1}^{N}\alpha_iαmin21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαi
s.t. ∑i=1Nαiyi=0\text{s.t. } \sum_{i=1}^{N}\alpha_i y_i = 0s.t. i=1∑Nαiyi=0
0⩽αi⩽C,i=1,2,⋯ ,N0 \leqslant \alpha_i \leqslant C, \quad i = 1,2,\cdots,N0⩽αi⩽C,i=1,2,⋯,N
线性支持向量机的对偶学习算法,首先求解对偶问题得到最优解 α∗\alpha^*α∗,然后求原始问题最优解 w∗w^*w∗ 和 b∗b^*b∗,得出分离超平面和分类决策函数。
对偶问题的解 α∗\alpha^*α∗ 中满足 αi∗>0\alpha_i^* > 0αi∗>0 的实例点 xix_ixi 称为支持向量。支持向量可在间隔边界上,也可在间隔边界与分离超平面之间,或者在分离超平面误分一侧。最优分离超平面由支持向量完全决定。
线性支持向量机学习等价于最小化二阶范数正则化的合页函数
∑i=1N[1−yi(w⋅xi+b)]++λ∥w∥2\sum_{i=1}^{N}[1 - y_i(w \cdot x_i + b)]_+ + \lambda\|w\|^2i=1∑N[1−yi(w⋅xi+b)]++λ∥w∥2
3. 非线性支持向量机
对于输入空间中的非线性分类问题,可以通过非线性变换将它转化为某个高维特征空间中的线性分类问题,在高维特征空间中学习线性支持向量机。由于在线性支持向量机学习的对偶问题里,目标函数和分类决策函数都只涉及实例与实例之间的内积,所以不需要显式地指定非线性变换,而是用核函数来替换当中的内积。核函数表示,通过一个非线性转换后的两个实例间的内积。具体地,K(x,z)K(x, z)K(x,z) 是一个核函数,或正定核,意味着存在一个从输入空间 X\mathcal{X}X 到特征空间 H\mathcal{H}H 的映射 ϕ(x):X→H\phi(x): \mathcal{X} \to \mathcal{H}ϕ(x):X→H,对任意 x,z∈Xx, z \in \mathcal{X}x,z∈X,有
K(x,z)=ϕ(x)⋅ϕ(z)K(x, z) = \phi(x) \cdot \phi(z)K(x,z)=ϕ(x)⋅ϕ(z)
对称函数 K(x,z)K(x, z)K(x,z) 为正定核的充要条件如下:对任意 xi∈Xx_i \in \mathcal{X}xi∈X,i=1,2,⋯ ,mi = 1, 2, \cdots, mi=1,2,⋯,m,任意正整数 mmm,对称函数 K(x,z)K(x, z)K(x,z) 对应的 Gram 矩阵是半正定的。
所以,在线性支持向量机学习的对偶问题中,用核函数 K(x,z)K(x, z)K(x,z) 替代内积,求解得到的就是非线性支持向量机
f(x)=sign(∑i=1Nαi∗yiK(x,xi)+b∗)f(x) = \text{sign}\left(\sum_{i=1}^{N}\alpha_i^* y_i K(x, x_i) + b^*\right)f(x)=sign(i=1∑Nαi∗yiK(x,xi)+b∗)
4. SMO 算法
SMO 算法是支持向量机学习的一种快速算法,其特点是不断地将原二次规划问题分解为只有两个变量的二次规划子问题,并对子问题进行解析求解,直到所有变量满足 KKT 条件为止。这样通过启发式的方法得到原二次规划问题的最优解。因为子问题有解析解,所以每次计算子问题都很快,虽然计算子问题次数很多,但在总体上还是高效的。