LWGANet: Addressing Spatial and Channel Redundancy in Remote Sensing Visual Tasks with Light-Weight Grouped Attention

LWGANet论文全面解析

一、研究背景与动机

1.1 核心问题

该论文针对遥感（RS）图像视觉分析中的两大固有冗余问题：

空间冗余（Spatial Redundancy）：遥感图像中包含大量同质化背景（道路、农田、海洋），显著目标稀疏分布，导致大量计算资源浪费在低价值区域
通道冗余（Channel Redundancy）：遥感图像尺度变化极端（从小型车辆到大型跑道），单一特征空间难以高效捕获多尺度目标，导致特征通道利用效率低下

1.2 现有方法的局限

现有轻量级网络（如MobileNetV2 ）主要为自然图像设计，采用同质化分组策略（如深度可分离卷积），无法有效解决遥感图像的特殊冗余问题：

CNN模型（如FasterNet）：局部表征强但缺乏全局感受野
Transformer模型（如EfficientFormerV2）：全局建模能力强但抑制高频空间信息

为什么Transformer模型抑制高频空间信息？

Transformer模型，特别是在图像处理中的应用（如EfficientFormerV2），具有很强的全局建模能力，能够捕捉长程依赖关系。然而，Transformer本身的架构和计算方式，使得它在捕捉全局信息时对局部高频特征（如纹理、边缘等细节信息）的抑制较强。

输入：一组token（图像patch的特征）

假设：8×8 = 64个patch

Q = input @ W_q # Query（我要找什么）

K = input @ W_k # Key（我是什么）

V = input @ W_v # Value（我的内容）

计算注意力权重

attention_weights = softmax(Q @ K.T / sqrt(d)) # 64×64矩阵

**关键特点**：每个位置都看**全局所有位置**

```

Patch 1 的输出 = 0.3×Patch1 + 0.1×Patch2 + ... + 0.05×Patch64

Patch 2 的输出 = 0.2×Patch1 + 0.4×Patch2 + ... + 0.03×Patch64

2.3 为什么抑制高频信息？

原因1：Patch化导致局部信息丢失

```

原始图像（224×224）：

┌───────────────────────────────┐

│ │││││ ←建筑物边缘（1像素宽） │

│ │││││ │

│ │

└───────────────────────────────┘

Vision Transformer处理：

Step 1: 切成16×16的patch → 14×14=196个patch

┌────┬────┬────┬────┐

│ P1 │ P2 │ P3 │... │ ← 每个patch内部做平均

├────┼────┼────┼────┤

│ P5 │ P6 │ P7 │... │

└────┴────┴────┴────┘

问题：

1像素宽的边缘在16×16 patch中被"稀释"
Patch内部求平均 → 细节模糊
边缘信息被平滑掉 ❌

卷积神经网络的局部感受野：相比之下，传统的卷积神经网络（CNN）通过卷积核的局部感受野，低通滤波器：只保留低频，去除高频，能够更好地保留高频空间信息（如边缘和细节），因为卷积操作具有强烈的局部特征捕捉能力。

举个例子：

在处理图像时，卷积神经网络（如VGG、ResNet等）会通过滑动窗口的方式逐步提取局部特征。高频信息（如边缘、纹理）通常通过小的卷积核进行提取，这样就能保留细节。
而Transformer模型（如EfficientFormerV2）虽然可以捕捉远距离的全局信息，但在计算时会平均各位置的信息，因此高频的局部细节信息容易被"平滑"掉，反而在全局特征上会更突出。

深度可分离卷积（Depthwise Separable Convolution）

**可视化**：

```

步骤1：Depthwise（每个通道单独卷积）

输入通道：独立卷积：中间结果：

┌──┐ ┌───┐ ┌──┐

│C1│─────────→│3×3│─────────────────→│D1│ ← 只看C1

│C2│─────────→│3×3│─────────────────→│D2│ ← 只看C2

│C3│─────────→│3×3│─────────────────→│D3│ ← 只看C3

└──┘ └───┘ └──┘

步骤2：Pointwise（1×1卷积混合）

中间结果： 1×1卷积：输出通道：

┌──┐ ┌─────┐ ┌──┐

│D1│─────────→│ │──────────────→│O1│

│D2│─────────→│1×1 │──────────────→│O2│

│D3│─────────→│ │──────────────→│O3│

└──┘ └─────┘ └──┘

参数量：

Depthwise: K×K×C_in×1 (每个通道一个核)
Pointwise: 1×1×C_in×C_out
总计：K×K×C_in + C_in×C_out

深度可分离卷积通过将标准的卷积操作分为两个部分来降低计算复杂度：
Depthwise Convolution：每个输入通道用一个独立的卷积核进行卷积，即每个通道独立地进行处理，没有跨通道的信息交互。
Pointwise Convolution：然后用 1×11 \times 11×1 卷积核对深度卷积的输出进行组合，进行跨通道的信息整合。
在深度可分离卷积中，所有通道都用相同的卷积核大小和处理方式（同质化）进行处理。每个通道的卷积操作并没有做差异化，和多通道的互相交互不强，而是每个通道独立处理。这有利于减少计算量，但也意味着缺少了对不同特征的区分和自适应处理。

二、核心贡献

2.1 四大主要贡献

识别双重冗余瓶颈：首次系统性地将空间和通道冗余作为遥感图像高效网络设计的关键瓶颈
LWGA模块：轻量级分组注意力模块，通过将通道解耦为专用的多尺度路径来解决通道冗余
TGFI模块：Top-K全局特征交互模块，通过稀疏交互机制高效建模全局上下文，缓解空间冗余
LWGANet架构：基于上述原理构建的新型轻量级骨干网络，在12个数据集、4大遥感任务上达到SOTA性能

三、方法论详解

3.1 整体架构

LWGANet采用四阶段层级结构：

空间分辨率依次降低：4×、8×、16×、32×
提供三个变体：L0、L1、L2（stem层通道数分别为32、64、96）
每阶段包含若干LWGA块，块数配置为[1,2,4,2]（L0/L1）或[1,4,4,2]（L2）

3.2 LWGA模块（核心创新）

异构分组策略

打破传统同质化分组范式，将输入特征分为4个非重叠路径，每个路径处理不同尺度：

路径	模块	功能	尺度
X₁	GPA（门控点注意力）	增强细粒度特征	点级细节
X₂	RLA（常规局部注意力）	捕获局部纹理	局部模式
X₃	SMA（稀疏中程注意力）	捕获中等范围上下文	中程结构
X₄	SGA（稀疏全局注意力）	建模长程依赖	全局上下文

各子模块详解

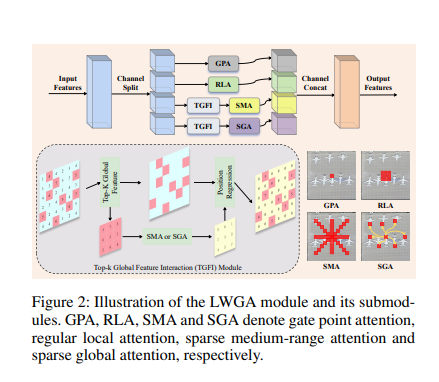
详细解析LWGA模块架构图

一、整体流程解读（顶部主流程）

完整数据流

复制代码

Input Features (H×W×C)
       ↓
[Channel Split] 通道分割
       ↓
   ┌───┴───┬───────┬───────┐
   ↓       ↓       ↓       ↓
  GPA     RLA   TGFI→SMA  TGFI→SGA
 (C/4)   (C/4)   (C/4)    (C/4)
   ↓       ↓       ↓       ↓
   └───┬───┴───────┴───────┘
       ↓
[Channel Concat] 通道拼接
       ↓
Output Features (H×W×C)

二、四个子模块详解

1️⃣ GPA (Gate Point Attention) - 门控点注意力

右上角可视化 ：呈现点状模式

复制代码

🔴 🔴    🔴
   🔴 🔴
🔴    🔴 🔴

功能：记住 1×1卷积 + 门控机制，扩展-压缩-门控，就可以实现对单个像素实现观察，实现像素级别的观察

捕获逐像素级别的细节
类似"显微镜"，放大观察每个点
门控三要素： 1. 值在零到一（[0,1]范围） 2. 乘法选通过（element-wise ×） 3. 控制信息流（filtering），决定信息的流通性

实现原理：

复制代码

# 1×1卷积 + 门控机制
X1 = input[:, :, :, 0:C//4]  # 取前1/4通道

# 扩展-压缩-门控
expanded = Conv1x1(X1, C//4 → C)      # 扩展到C通道
compressed = Conv1x1(expanded, C → C//4)  # 压缩回C/4
gate = Sigmoid(compressed)              # 生成0-1权重

output = X1 + gate * X1  # 门控增强

适用场景：

✅ 小车辆检测（10×10像素）
✅ 建筑物角点
✅ 精细边缘
✅ 窗户、标志等细小物体

为什么叫"Point"：只关注单个像素点，不看邻域

2️⃣ RLA (Regular Local Attention) - 常规局部注意力

右侧第二行可视化 ：呈现局部密集模式

复制代码

▓▓▓▓▓
▓▓█▓▓  ← 中心像素周围的3×3区域
▓▓▓▓▓

功能：

捕获局部纹理和模式
类似"放大镜"，看清局部细节

实现原理：

复制代码

# 标准3×3卷积
X2 = input[:, :, :, C//4:C//2]

output = Conv3x3(X2)  # 简单直接的局部卷积
output = BN(output)
output = Activation(output)

适用场景：

✅ 道路纹理
✅ 建筑物表面材质
✅ 小型结构物（20-50像素）
✅ 规则形状物体

为什么叫"Regular"：使用标准的、规则的卷积核

3️⃣ SMA (Sparse Medium-range Attention) - 稀疏中程注意力

右侧第三行可视化 ：呈现十字形/四方向模式

复制代码

    ↑
    │
←───█───→  ← 四个方向的稀疏连接
    │
    ↓

功能：

捕获中等距离的上下文（11×11范围）
类似"望远镜"，看到中等范围
适合不规则形状物体

为什么先经过TGFI？

因为要处理11×11范围，直接计算太贵：

复制代码

# ❌ 不用TGFI的问题
# 假设特征图64×64
for each pixel in 64×64:  # 4096个像素
    compute 11×11 attention  # 每个像素看121个邻居
    # 总计算量：4096 × 121 ≈ 50万次

# ✅ 用TGFI优化
X3 = input[:, :, :, C//2:3*C//4]

# Step 1: TGFI稀疏采样 (3×3区域选Top-1)
X3_sparse = TGFI_downsample(X3, factor=3)  
# 64×64 → 21×21 (减少到原来的1/9)

# Step 2: 在稀疏特征上做中程注意力
# 四方向注意力公式（论文Eq.2）
attention = FourDirectionAttention(X3_sparse, window=11)
# 水平：左右各5个位置
# 垂直：上下各5个位置  
# 对角1：左上-右下各5个位置
# 对角2：左下-右上各5个位置

# Step 3: TGFI恢复到原始尺寸
attention_restored = TGFI_upsample(attention, positions)
output = attention_restored * X3

计算量对比：

复制代码

不用TGFI: 64×64 × 11×11 = 497,664 次操作
用TGFI:   21×21 × 11×11 = 53,361 次操作
           ↓
         节省 90% 计算量！

适用场景：

✅ 不规则港口结构
✅ 停车场（需要看到多辆车的关系）
✅ 河流、道路（细长形状）
✅ 中型建筑群（50-150像素）

4️⃣ SGA (Sparse Global Attention) - 稀疏全局注意力

右侧第四行可视化 ：呈现更稀疏的全局模式

复制代码

🔴 ·  · 🔴 ·  🔴
·  ·  🔴 ·  ·  ·
·  🔴 ·  ·  🔴 ·
🔴 ·  ·  🔴 ·  ·

功能：

建模长程依赖 和全局场景理解
类似"卫星视角"，纵观全局

为什么先经过TGFI？

全局注意力的复杂度是二次方：

复制代码

# ❌ 不用TGFI的恐怖计算量
# Self-Attention复杂度：O(N²)
# N = H × W

64×64特征图：
N = 4,096
注意力矩阵：4,096 × 4,096 = 16,777,216 (1600万！)

# ✅ 用TGFI优化
X4 = input[:, :, :, 3*C//4:C]

# Stage 1-2: 特征图大，用卷积近似
if stage in [1, 2]:
    X4_sparse = TGFI_downsample(X4, factor=2)  # 64×64 → 32×32
    # 用5×5分组卷积 + 7×7膨胀卷积近似全局
    conv_global = Conv5x5_grouped(X4_sparse)
    conv_dilated = Conv7x7_dilated(conv_global, dilation=3)
    output = TGFI_upsample(conv_dilated)
    
# Stage 3: 特征图中等，用稀疏注意力
elif stage == 3:
    X4_sparse = TGFI_downsample(X4, factor=2)  # 32×32 → 16×16
    # 注意力矩阵：256×256（可接受）
    attention = MultiHeadAttention(X4_sparse, heads=4)
    output = TGFI_upsample(attention)
    
# Stage 4: 特征图小，直接全密集注意力
else:  # stage == 4
    # 16×16特征图，注意力矩阵：256×256（很小）
    output = MultiHeadAttention(X4, heads=4)  # 不需要TGFI

计算量对比（Stage 2为例）：

复制代码

不用TGFI:
Self-Attention(64×64) = 4096² = 16,777,216 次乘法

用TGFI:
Self-Attention(32×32) = 1024² = 1,048,576 次乘法
                        ↓
                    节省 94% 计算量！

适用场景：

✅ 机场跑道全局布局
✅ 大型港口的整体结构
✅ 城市街区的整体规划
✅ 大型建筑（>200像素）

三、TGFI模块详解（底部虚线框）

可视化解读

复制代码

底部示意图展示的三步流程：

┌─────────────────────────────────────┐
│  Step 1: 稀疏采样                    │
│  ┌────────┐      ┌──────┐          │
│  │█ █ █  │      │█ █  │           │
│  │ █  █ █│  →   │ █ █ │  (Top-K) │
│  │█  █ █ │      └──────┘           │
│  └────────┘       更少的token       │
│  密集特征          稀疏特征          │
└─────────────────────────────────────┘
          ↓
┌─────────────────────────────────────┐
│  Step 2: SMA or SGA处理              │
│  ┌──────┐      ┌──────┐            │
│  │█ █  │      │▓ ▓  │             │
│  │ █ █ │  →   │ ▓ ▓ │  (增强)     │
│  └──────┘      └──────┘             │
│  稀疏特征       增强特征             │
└─────────────────────────────────────┘
          ↓
┌─────────────────────────────────────┐
│  Step 3: 位置恢复 (Position Regression)│
│  ┌──────┐      ┌────────┐          │
│  │▓ ▓  │      │▓ · ▓ · │          │
│  │ ▓ ▓ │  →   │· ▓ · ▓ │  (插值)  │
│  └──────┘      │▓ · ▓ · │          │
│               └────────┘           │
│  增强特征       恢复到原始大小        │
└─────────────────────────────────────┘

TGFI的三个关键步骤

Step 1: Top-K稀疏采样

复制代码

def TGFI_sample(features, factor):
    """
    features: H×W×C
    factor: 下采样因子（2或3）
    """
    # 使用MaxPool2d选择最显著特征
    sparse_features, indices = F.max_pool2d(
        features,
        kernel_size=factor,
        stride=factor,
        return_indices=True  # 🔑 记住位置！
    )
    
    # H×W → H/factor × W/factor
    return sparse_features, indices

可视化：

复制代码

原始特征图（16×16）- 激活值：
┌─────────────────────┐
│ 0.1  0.3  0.2  0.1 │
│ 0.2  0.9  0.1  0.3 │  ← 0.9最显著
│ 0.1  0.2  0.8  0.2 │
│ 0.3  0.1  0.2  7.5 │  ← 7.5最显著
└─────────────────────┘

↓ MaxPool2d(kernel=2, stride=2)

稀疏特征图（8×8）- 只保留最强的：
┌──────────┐
│ 0.9  0.3 │
│ 0.3  7.5 │
└──────────┘

同时记录位置索引：
indices = [(1,1), (1,3), (3,1), (3,3)]

Step 2: 子空间交互（SMA或SGA）

复制代码

# 在稀疏特征上执行计算密集操作
enhanced = SMA_or_SGA(sparse_features)

# SMA的四方向注意力
if module == "SMA":
    enhanced = FourDirectionAttention(
        sparse_features, 
        window=11
    )

# SGA的全局注意力
elif module == "SGA":
    enhanced = MultiHeadSelfAttention(
        sparse_features,
        num_heads=4
    )

Step 3: 位置回归/恢复

复制代码

def TGFI_restore(enhanced, indices, original_size):
    """
    enhanced: 增强后的稀疏特征
    indices: 之前记录的位置
    original_size: 原始尺寸
    """
    # 使用MaxUnpool2d恢复到原始位置
    restored = F.max_unpool2d(
        enhanced,
        indices,  # 🔑 用之前保存的位置
        kernel_size=factor,
        stride=factor,
        output_size=original_size
    )
    
    # 非采样位置用插值填充
    restored = F.interpolate(
        restored,
        size=original_size,
        mode='bilinear'
    )
    
    return restored

可视化：

复制代码

增强稀疏特征（8×8）：
┌──────────┐
│ 2.5  1.8 │
│ 1.2  9.3 │
└──────────┘

↓ MaxUnpool2d + 插值

恢复特征图（16×16）：
┌─────────────────────┐
│ ·   ·   ·   ·      │
│ ·  2.5  ·  1.8     │  ← 2.5和1.8放回原位
│ ·   ·   ·   ·      │
│ ·  1.2  ·  9.3     │  ← 1.2和9.3放回原位
└─────────────────────┘

↓ 插值填充空白位置

完整特征图（16×16）：
┌─────────────────────┐
│ 1.5  2.0  2.5  2.1 │  ← 插值填充
│ 1.8  2.5  2.1  1.8 │
│ 1.3  1.8  1.5  2.0 │
│ 1.1  1.2  5.0  9.3 │
└─────────────────────┘

四、右侧注意力模式可视化

GPA - 点状模式

复制代码

原图：              注意力图：
┌────────┐         ┌────────┐
│ 🏢🏢🏢  │         │ 🔴🔴🔴  │  ← 建筑角点
│ 🏢🏢🏢  │   →     │ 🔴  🔴  │
│ 🏢🏢🏢  │         │ 🔴🔴🔴  │  ← 关注关键点
└────────┘         └────────┘

特点：离散的点，关注关键位置

RLA - 局部密集模式

复制代码

原图：              注意力图：
┌────────┐         ┌────────┐
│  🚗     │         │ ▓▓▓    │  ← 车辆周围3×3
│        │   →     │ ▓█▓    │  ← 密集覆盖
│        │         │ ▓▓▓    │
└────────┘         └────────┘

特点：小范围密集覆盖

SMA - 十字形模式

复制代码

原图：              注意力图：
┌────────┐         ┌────────┐
│   ⚓    │         │   ↑    │  
│        │   →     │ ←🔴→   │  ← 四方向扩散
│        │         │   ↓    │  ← 11×11范围
└────────┘         └────────┘

特点：中等范围，四方向稀疏连接

SGA - 稀疏全局模式

复制代码

原图：              注意力图：
┌────────┐         ┌────────┐
│🏢  ✈️  │         │🔴· ·🔴 │  ← 远距离连接
│        │   →     │· 🔴 · ·│  ← 稀疏采样点
│  🚢    │         │· ·  🔴 │  ← 全局视野
└────────┘         └────────┘

特点：全图范围，稀疏连接关键区域

五、为什么SMA和SGA需要TGFI？

对比表

特征	GPA	RLA	SMA	SGA
感受野	1×1	3×3	11×11	全局
计算复杂度	O(C)	O(9C)	O(121C)	O(N²)
需要TGFI?	❌ 不需要	❌ 不需要	✅ 需要	✅ 需要
原因	单点计算	邻域小	邻域大	全局巨大

具体原因

GPA不需要TGFI：

复制代码

# 1×1卷积，每个像素独立处理
for pixel in image:
    output = W @ pixel  # 只是矩阵乘法
# 复杂度：O(HWC) ← 线性，可接受

RLA不需要TGFI：

复制代码

# 3×3卷积，局部邻域
for pixel in image:
    output = sum(W[i,j] * neighbors[i,j])  # 只看9个邻居
# 复杂度：O(9HWC) ← 仍是线性，硬件优化好

SMA需要TGFI：

复制代码

# ❌ 不用TGFI
for pixel in 64×64:  # 4096像素
    # 四方向，每方向5个位置
    attention = compute_11x11_attention(pixel)  # 看121个邻居
# 复杂度：O(121HWC) ← 太大了！

# ✅ 用TGFI
for pixel in 21×21:  # 441像素（稀疏后）
    attention = compute_11x11_attention(pixel)
# 复杂度：降低到原来的 1/9

SGA需要TGFI：

复制代码

# ❌ 不用TGFI
attention_matrix = Q @ K.T  # (HW) × (HW)
# 64×64特征图：4096 × 4096 = 1600万次计算！

# ✅ 用TGFI
attention_matrix = Q_sparse @ K_sparse.T  # (HW/4) × (HW/4)
# 32×32稀疏特征：1024 × 1024 = 100万次计算
# 降低到原来的 1/16！

六、完整流程示例

假设处理一个64×64×256的特征图：

复制代码

# 输入
input = torch.randn(1, 64, 64, 256)

# === Channel Split ===
X1 = input[:, :, :, 0:64]       # GPA通道
X2 = input[:, :, :, 64:128]     # RLA通道
X3 = input[:, :, :, 128:192]    # SMA通道
X4 = input[:, :, :, 192:256]    # SGA通道

# === 并行处理 ===

# 路径1: GPA（不需要TGFI）
R1 = GPA(X1)  # 64×64×64

# 路径2: RLA（不需要TGFI）
R2 = RLA(X2)  # 64×64×64

# 路径3: SMA（需要TGFI）
X3_sparse, idx3 = TGFI_sample(X3, factor=3)  # 21×21×64
R3_sparse = SMA(X3_sparse, window=11)        # 21×21×64
R3 = TGFI_restore(R3_sparse, idx3, (64,64))  # 64×64×64

# 路径4: SGA（需要TGFI）
X4_sparse, idx4 = TGFI_sample(X4, factor=2)  # 32×32×64
R4_sparse = SGA(X4_sparse, heads=4)          # 32×32×64
R4 = TGFI_restore(R4_sparse, idx4, (64,64))  # 64×64×64

# === Channel Concat ===
output = torch.cat([R1, R2, R3, R4], dim=-1)  # 64×64×256

七、核心设计理念总结

异构设计哲学

复制代码

传统方法（同质化）：
256通道 → 全部做3×3卷积
问题：一刀切，无法适应多尺度

LWGANet（异构化）：
64通道 → 专注点级细节（GPA）     成本：低
64通道 → 专注局部纹理（RLA）     成本：低
64通道 → 专注中程结构（SMA+TGFI）成本：中
64通道 → 专注全局上下文（SGA+TGFI）成本：中

优势：
1. 各司其职，通道利用率高
2. TGFI控制成本，SMA/SGA能负担得起
3. 多尺度全覆盖，无短板

TGFI的价值

复制代码

不是所有路径都需要TGFI！

需要TGFI的条件：
✅ 感受野大（>5×5）
✅ 计算复杂度高（O(N²)或O(k²)）
✅ 遥感图像的显著性稀疏分布

GPA/RLA不需要：计算量小，直接算更快
SMA/SGA必须有：不然计算量爆炸

希望这个详细的图解能帮你完全理解LWGA模块的设计！

核心要点：

四路异构：GPA(点)/RLA(局部)/SMA(中程)/SGA(全局)
TGFI作用：降低SMA和SGA的计算成本（空间维度降采样）
SMA含义 ：Sparse Medium-range Attention（稀疏中程注意力）
SGA含义 ：Sparse Global Attention（稀疏全局注意力）

四、实验设计

4.1 数据集覆盖（12个数据集）

任务	数据集	规模	类别数
场景分类	UCM	2,100张	21
	AID	10,000张	30
	NWPU-RESISC45	31,500张	45
旋转目标检测	DOTA 1.0	2,806张	15
	DOTA 1.5	2,806张	16
	DIOR-R	23,463张	20
语义分割	UAVid	300张	8
	LoveDA	5,987张	7
变化检测	LEVIR-CD	637对	2
	WHU-CD	1对	2
	CDD-CD	11对	2
	SYSU-CD	20,000对	2

4.2 训练配置

分类任务：

从头训练300 epoch
AdamW优化器（lr=1e-4，weight decay=5e-2）
Cosine学习率衰减
批量大小64

检测任务：

ImageNet-1K预训练
Oriented R-CNN检测器
训练36 epoch

分割任务：

UnetFormer作为分割头
UAVid：30 epoch，batch size=8
LoveDA：70 epoch，batch size=16

五、实验结果

5.1 场景分类性能

LWGANet-L0表现（1.72M参数）：

NWPU：95.49%（超越StarNet S1 +1.19%）
AID：94.60%
UCM：98.57%
GPU速度：13,234 FPS

LWGANet-L2表现（13.0M参数）：

NWPU：96.17%（新SOTA）
GPU速度：3,308 FPS
优于所有同等规模竞争者

5.2 旋转目标检测

DOTA 1.0测试集：

LWGANet-L2：79.02% mAP（新SOTA）
超越PKINet-S（78.39%）
参数更少（29.2M vs 30.8M）
速度更快（19.4 FPS vs 5.4 FPS）

DOTA 1.5测试集：

LWGANet-L2：72.91% mAP
在所有16个类别上表现均衡

5.3 语义分割

UAVid测试集：

LWGANet-L2：69.1% mIoU
超越ResNet18 +1.3%
在Moving Car和Human等困难类别表现最佳

LoveDA测试集：

LWGANet-L2：53.6% mIoU（新SOTA）
超越RSSFormer、LoveNAS等专用模型

5.4 变化检测

集成到A2Net解码器（L0版本）：

LEVIR-CD：84.94% IoU
WHU-CD：90.24% IoU

集成到CLAFA解码器（L2版本）：

在所有4个数据集上达到新SOTA
WHU-CD提升+1.18% IoU

六、消融实验

6.1 核心组件验证

配置	NWPU Acc	DOTA mAP	LoveDA mIoU	LEVIR IoU
仅RLA（基线）	95.35%	69.64%	48.61%	83.66%
RLA+SMA+SGA	95.83%	70.56%	48.80%	83.10%
全模型（+TGFI）	95.49%	70.08%	49.20%	82.93%

关键发现：

TGFI不仅降低空间冗余，还显著加速LWGA模块（FPS从6052提升至13,234）
四路径协同效果优于单一模块

6.2 单模块对比实验

在DOTA 1.0验证集上测试仅使用单一注意力类型的网络：

方法	mAP	特点
仅GPA	68.4%	聚焦点状细节
仅RLA	70.3%	局部纹理强
仅SMA	70.5%	中等范围上下文
仅SGA	71.0%	全局依赖
LWGANet-L2	74.1%	协同增强

说明异构多路径设计产生协同效应，而非简单叠加。

七、创新点总结

7.1 理论创新

异构分组范式：从同质化分组转向异构多尺度表征，每个通道组专注特定尺度
双冗余协同解决：LWGA解决通道冗余，TGFI解决空间冗余，两者相辅相成

7.2 技术创新

阶段自适应全局注意力：根据特征图大小动态调整全局建模策略
非参数化稀疏采样：TGFI使用简单的最大池化，避免学习额外参数

7.3 工程创新

硬件友好设计：使用标准PyTorch操作，易于部署
多平台高效：在GPU、CPU、ARM上均保持高吞吐量

八、局限性与未来工作

8.1 已识别的局限

架构自适应性
- 当前设计为静态，通道分配和超参数固定
- 建议：引入NAS学习最优配置
实际部署效率
- 异构操作可能产生执行开销
- 建议：算子融合、定制CUDA核心

8.2 潜在扩展方向

领域泛化：该双冗余问题在数字病理学、高分辨率文档分析中同样存在
动态架构：自适应调整各路径的计算资源分配
极致轻量化：针对边缘设备的进一步优化

九、关键洞察

9.1 设计哲学

"功能专一化优于一刀切"：

不同尺度目标需要不同的特征提取策略
强制所有通道执行相同操作会导致资源浪费

9.2 遥感特性利用

"显著性稀疏分布"：

遥感图像中有效信息占比小
TGFI通过Top-K采样充分利用这一特性

9.3 工程与科学的平衡

理论上创新（异构分组）
实践上高效（硬件友好）
通用性强（4大任务12数据集）

十、总结评价

优势

✅ 问题定义清晰 ：双冗余概念针对遥感图像特点 ✅ 方法设计合理 ：LWGA和TGFI相互配合 ✅ 实验验证充分 ：跨任务、跨数据集的广泛评估 ✅ 实用性强 ：在多硬件平台保持高效 ✅ 可复现性好：详细的实现细节和开源承诺

潜在改进空间

⚠️ 消融实验可增加统计显著性检验 ⚠️ 可探索自适应通道分配策略 ⚠️ 需进一步优化边缘设备部署

学术价值

该论文为遥感图像处理提供了新的架构设计范式，其核心思想（针对数据特性的专用路径设计）对其他视觉领域也有启发意义。在轻量级网络设计中，从"如何压缩"转向"如何智能分配"，是一个重要的思路转变。

LWGANet：两大核心模块：TGFI（减空间冗余）和 LWGA（减通道冗余。

LWGANet: Addressing Spatial and Channel Redundancy in Remote Sensing Visual Tasks with Light-Weight Grouped Attention

LWGANet论文全面解析

一、研究背景与动机

1.1 核心问题

1.2 现有方法的局限

为什么Transformer模型抑制高频空间信息？

输入：一组token（图像patch的特征）

假设：8×8 = 64个patch

计算注意力权重

原因1：Patch化导致局部信息丢失

举个例子：

深度可分离卷积（Depthwise Separable Convolution）

二、核心贡献

2.1 四大主要贡献

三、方法论详解

3.1 整体架构

3.2 LWGA模块（核心创新）

异构分组策略

各子模块详解

详细解析LWGA模块架构图

一、整体流程解读（顶部主流程）

完整数据流

二、四个子模块详解

1️⃣ GPA (Gate Point Attention) - 门控点注意力

2️⃣ RLA (Regular Local Attention) - 常规局部注意力

3️⃣ SMA (Sparse Medium-range Attention) - 稀疏中程注意力

4️⃣ SGA (Sparse Global Attention) - 稀疏全局注意力

三、TGFI模块详解（底部虚线框）

可视化解读

TGFI的三个关键步骤

Step 1: Top-K稀疏采样

Step 2: 子空间交互（SMA或SGA）

Step 3: 位置回归/恢复

四、右侧注意力模式可视化

GPA - 点状模式

RLA - 局部密集模式

SMA - 十字形模式

SGA - 稀疏全局模式

五、为什么SMA和SGA需要TGFI？

对比表

具体原因

六、完整流程示例

七、核心设计理念总结

异构设计哲学

TGFI的价值

四、实验设计

4.1 数据集覆盖（12个数据集）

4.2 训练配置

五、实验结果

5.1 场景分类性能

5.2 旋转目标检测

5.3 语义分割

5.4 变化检测

六、消融实验

6.1 核心组件验证

6.2 单模块对比实验

七、创新点总结

7.1 理论创新

7.2 技术创新

7.3 工程创新

八、局限性与未来工作

8.1 已识别的局限

8.2 潜在扩展方向

九、关键洞察

9.1 设计哲学

9.2 遥感特性利用

9.3 工程与科学的平衡

十、总结评价

优势

潜在改进空间

学术价值