机器学习高阶教程＜1＞优化理论：破解优化器的底层密码

引言

先跟大家说声抱歉，周六周日没能按时更新------因为我去上海参加了C++40th的盛典，还见到了C++祖师爷本贾尼，现场氛围实在太燃，完全沉浸其中了！今天上午赶回来处理完杂事，晚上简单吃过饭就立刻坐下来，把这篇欠大家的高阶内容安排上。

还记得我们在入门和进阶篇里，聊过模型训练的基本逻辑和超参数调优的核心思路吗？今天我们要钻得更深------那些让模型"学会学习"的优化器，到底藏着怎样的数学玄机？

你肯定有过这种体验：用梯度下降训练模型时，明明loss在下降，却卡在某个值再也动不了；换了Adam之后突然"柳暗花明"，但又说不清楚为什么。这篇文章不会扔给你满屏公式就跑路------我们会从"梯度下降的收敛性证明"这个核心痛点切入，拆透Adam、AdaGrad的设计逻辑，最后直面非凸优化的"终极挑战"。放心，每个数学原理都会配一个"生活翻译官"，读到结尾你会发现：高阶优化理论，其实是把"试错经验"写成了数学公式。

先搞懂：为什么梯度下降一定会"有效"？------收敛性证明的通俗解读

在入门篇里，我们只说"梯度是函数下降最快的方向"，但没敢深究：沿着这个方向走，一定能走到最低点吗？会不会绕圈？会不会走得越来越慢最后停在半路？这就是收敛性证明要回答的问题------它不是"证明公式"，而是"证明梯度下降这套操作的可靠性"。

先请出我们的"生活模型"：假设你站在大雾里的山坡上，要走到山底（对应loss最小值）。你看不见全局，只能感觉到脚下的坡度（梯度），于是决定"每次都往最陡的地方走一小步"------这就是梯度下降的核心逻辑。现在要证明的是：只要你走的步长（学习率）合适，早晚能走到山底（或足够近的地方）。

关键前提：" Lipschitz 连续"------山坡不会突然变垂直

收敛性证明的第一个假设是"梯度满足Lipschitz连续"，听着吓人，翻译过来就是：山坡的坡度变化是平缓的，不会突然从30度变成90度。就像你走在普通山坡上，不会突然一脚踩空变成悬崖------这是梯度下降能"稳步下山"的基础。

如果没有这个前提呢？比如损失函数是"锯齿状"的，梯度一会儿正一会儿负，你按梯度走就会像在楼梯上跳来跳去，永远到不了底。好在机器学习里的大多数损失函数（比如MSE、交叉熵）都满足这个条件，这也是梯度下降能成为"万金油"的原因。

核心不等式："步长不能太大也不能太小"的数学依据

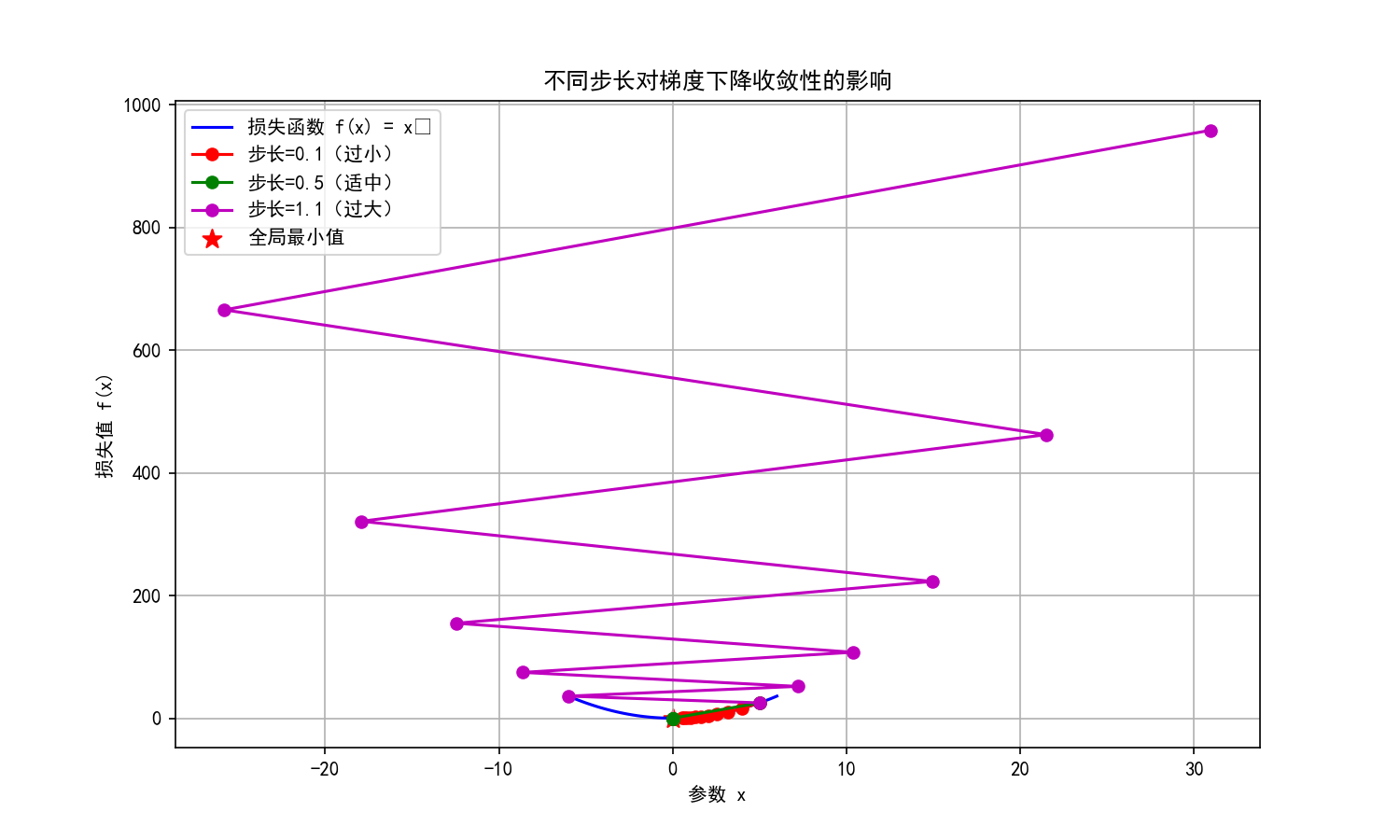
接下来是证明的核心：通过"梯度 Lipschitz 连续"可以推导出一个关键不等式（这里不写公式，只说结论）：每次迭代后，损失函数的下降量和步长、梯度大小直接相关。具体来说我们可以用一段简单的Python代码绘制不同步长下梯度下降的轨迹，直观感受差异：

运行代码后会得到这样的可视化结果：

图片的python代码：

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

import numpy as np

# 设置中文字体和负号显示
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 定义一个简单的凸函数 f(x) = x²（模拟损失函数）
def f(x):
    return x ** 2

# 梯度计算 f'(x) = 2x
def grad_f(x):
    return 2 * x

# 梯度下降实现
def gradient_descent(init_x, lr, iterations):
    x_history = [init_x]
    for i in range(iterations):
        grad = grad_f(x_history[-1])
        new_x = x_history[-1] - lr * grad
        x_history.append(new_x)
    return np.array(x_history)

# 三种不同步长的实验
lr_small = 0.1    # 步长过小
lr_ideal = 0.5   # 步长适中
lr_large = 1.1    # 步长过大
init_x = 5        # 初始位置
iterations = 10   # 迭代次数

x_small = gradient_descent(init_x, lr_small, iterations)
x_ideal = gradient_descent(init_x, lr_ideal, iterations)
x_large = gradient_descent(init_x, lr_large, iterations)

# 绘制结果
x = np.linspace(-6, 6, 100)
y = f(x)

plt.figure(figsize=(10, 6))
plt.plot(x, y, 'b-', label='损失函数 f(x) = x²')
plt.plot(x_small, f(x_small), 'ro-', label=f'步长={lr_small}（过小）')
plt.plot(x_ideal, f(x_ideal), 'go-', label=f'步长={lr_ideal}（适中）')
plt.plot(x_large, f(x_large), 'mo-', label=f'步长={lr_large}（过大）')
plt.scatter(0, 0, c='red', s=100, marker='*', label='全局最小值')
plt.xlabel('参数 x')
plt.ylabel('损失值 f(x)')
plt.title('不同步长对梯度下降收敛性的影响')
plt.legend()
plt.grid(True)
plt.savefig('gradient_descent_lr_effect.png', dpi=300, bbox_inches='tight')
plt.show()

从图中能清晰看到三种情况的差异：

如果步长太小：每次下降量都很小，需要迭代无数次才能到山底（就像小碎步下山，走到天黑还没到山脚）；
只有步长"恰到好处"（通常和Lipschitz常数成反比），才能保证loss每次都在下降，并且最终会无限接近最小值。
如果步长太大：虽然单次下降多，但可能"冲过山顶"，下次迭代loss反而上升（就像下山时一步跨太大，摔进对面的小土坡）；

这里插一个"心理学小技巧"：很多人看到"收敛性"就想逃，但请记住------证明的本质是"找规律"，而不是"炫技"。就像你通过多次试错发现"步长设为0.01时模型收敛最快"，数学家只是把这个经验用公式验证了而已。

灵魂拷问："收敛到最小值"还是"局部最小值"？

收敛性证明通常只能保证"收敛到局部最小值"，这就像你在连绵的群山里，按梯度走只能走到脚下山坡的谷底，却不一定是整个山脉的最低点。但别慌------机器学习实践中，大部分局部最小值的性能已经足够好，这也是我们敢用梯度下降的重要原因。而这个"局部最优"的痛点，正是后面非凸优化要解决的核心问题。

再升级：为什么Adam比"朴素梯度下降"更聪明？------自适应优化器的数学逻辑

理解了梯度下降的收敛性，你就会发现它的"致命缺点"：所有参数都用同一个步长更新。这就像你用同样的力气迈每一步下山，但有些地方坡度缓（对应小梯度参数），有些地方坡度陡（对应大梯度参数）------用同样的步长，缓坡走不动，陡坡容易冲过。

而Adam、AdaGrad这些自适应优化器，本质就是"给不同参数定制不同步长"。它们的数学原理看似复杂，其实都是围绕"两个核心问题"设计的：

问题1：如何判断"参数的重要性"？------AdaGrad的"历史梯度加权"

先看AdaGrad（自适应梯度下降）的思路：经常更新的参数（历史梯度大），给它小步长；偶尔更新的参数（历史梯度小），给它大步长。这就像老师批改作业：对经常出错的知识点（大梯度参数），每次只改一点慢慢纠正；对偶尔出错的知识点（小梯度参数），一次讲透快速解决。

它的数学实现很巧妙：用"历史梯度的平方和开根号"来做步长的分母。公式是这样的（别怕，我们翻译）：

θ = θ - (η / √(G + ε)) * g

其中G是"从训练开始到现在的梯度平方和"。翻译过来就是：某个参数的历史梯度越大（G越大），步长就越小；反之则越大。ε是为了防止分母为0的小常数，相当于"安全垫"。

比如在训练图片分类模型时，"边缘检测"相关的参数（梯度大）会慢慢更新，而"细节纹理"相关的参数（梯度小）会快速更新------这样模型就能兼顾"整体结构"和"细节特征"。

问题2：如何避免"步长越来越小"？------Adam的"动量+滑动平均"

AdaGrad有个缺点：训练时间越长，G越大，步长会越来越小，最后可能"停在半路"。就像你下山时，越走步长越小，最后干脆不动了。而Adam（自适应动量估计）解决了这个问题，它相当于"给AdaGrad加了两个buff"：

动量（Momentum）：借鉴物理中的"惯性"概念，更新参数时不仅考虑当前梯度，还考虑上一次的更新方向。就像下山时如果前一步是往南走，这一步即使梯度稍微偏东，也会带着向南的惯性------这样能避免在"小沟壑"里来回震荡。
滑动平均（Exponential Moving Average）：不用"所有历史梯度的平方和"，而是用"最近梯度的加权平均"。就像老师批改作业时，更看重"最近几次的表现"而不是"开学时的错误"------这样步长不会因为早期的大梯度而一直变小。

这两个buff的数学实现，就是Adam公式里的m和v（一阶矩和二阶矩）：m是梯度的滑动平均（管动量），v是梯度平方的滑动平均（管自适应步长）。最后再用"偏差修正"解决训练初期m和v偏小的问题------一套组合拳下来，Adam既灵活又稳定，难怪会成为深度学习的"默认优化器"。我们同样用Python代码对比SGD和Adam在二维非凸函数上的优化轨迹：

python代码如下：

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体和负号显示
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 定义一个二维非凸函数（模拟复杂模型的损失函数）
def non_convex_f(x, y):
    return x ** 2 + 10 * np.sin(x) + y ** 2 + 5 * np.sin(y)

# 计算梯度
def grad_non_convex(x, y):
    grad_x = 2 * x + 10 * np.cos(x)
    grad_y = 2 * y + 5 * np.cos(y)
    return np.array([grad_x, grad_y])

# SGD实现
def sgd(init_point, lr, iterations):
    point_history = [init_point]
    for i in range(iterations):
        grad = grad_non_convex(*point_history[-1])
        new_point = point_history[-1] - lr * grad
        point_history.append(new_point)
    return np.array(point_history)

# Adam实现
def adam(init_point, lr, beta1=0.9, beta2=0.999, eps=1e-8, iterations=100):
    point_history = [init_point]
    m = np.zeros_like(init_point)  # 一阶矩（动量）
    v = np.zeros_like(init_point)  # 二阶矩（自适应步长）
    for t in range(1, iterations + 1):
        grad = grad_non_convex(*point_history[-1])
        # 更新一阶矩和二阶矩
        m = beta1 * m + (1 - beta1) * grad
        v = beta2 * v + (1 - beta2) * grad ** 2
        # 偏差修正
        m_hat = m / (1 - beta1 ** t)
        v_hat = v / (1 - beta2 ** t)
        # 更新参数
        new_point = point_history[-1] - lr * m_hat / (np.sqrt(v_hat) + eps)
        point_history.append(new_point)
    return np.array(point_history)

# 实验参数设置
init_point = np.array([4.0, 3.0])  # 初始位置（远离最优解）
lr_sgd = 0.05                      # SGD学习率
lr_adam = 0.1                      # Adam学习率
iterations = 50                    # 迭代次数

# 运行两种优化器
sgd_history = sgd(init_point, lr_sgd, iterations)
adam_history = adam(init_point, lr_adam, iterations=iterations)

# 绘制优化轨迹
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = non_convex_f(X, Y)

plt.figure(figsize=(12, 8))
contour = plt.contourf(X, Y, Z, 50, cmap='viridis', alpha=0.8)
plt.colorbar(contour, label='损失值')
plt.contour(X, Y, Z, 10, colors='black', linewidths=0.5)
plt.plot(sgd_history[:, 0], sgd_history[:, 1], 'ro-', linewidth=2, label='SGD')
plt.plot(adam_history[:, 0], adam_history[:, 1], 'go-', linewidth=2, label='Adam')
plt.scatter(init_point[0], init_point[1], c='red', s=150, marker='*', label='初始位置')
# 标记全局最小值（通过数值计算得到）
min_points = np.array([[np.pi, np.pi], [-np.pi, -np.pi]])
plt.scatter(min_points[:, 0], min_points[:, 1], c='yellow', s=150, marker='*', label='全局最小值')
plt.xlabel('参数 x')
plt.ylabel('参数 y')
plt.title('SGD vs Adam 在非凸函数上的优化轨迹对比')
plt.legend()
plt.grid(True)
plt.savefig('sgd_vs_adam_trajectory.png', dpi=300, bbox_inches='tight')
plt.show()

运行代码后得到的对比图如下，能明显看到Adam的优势：

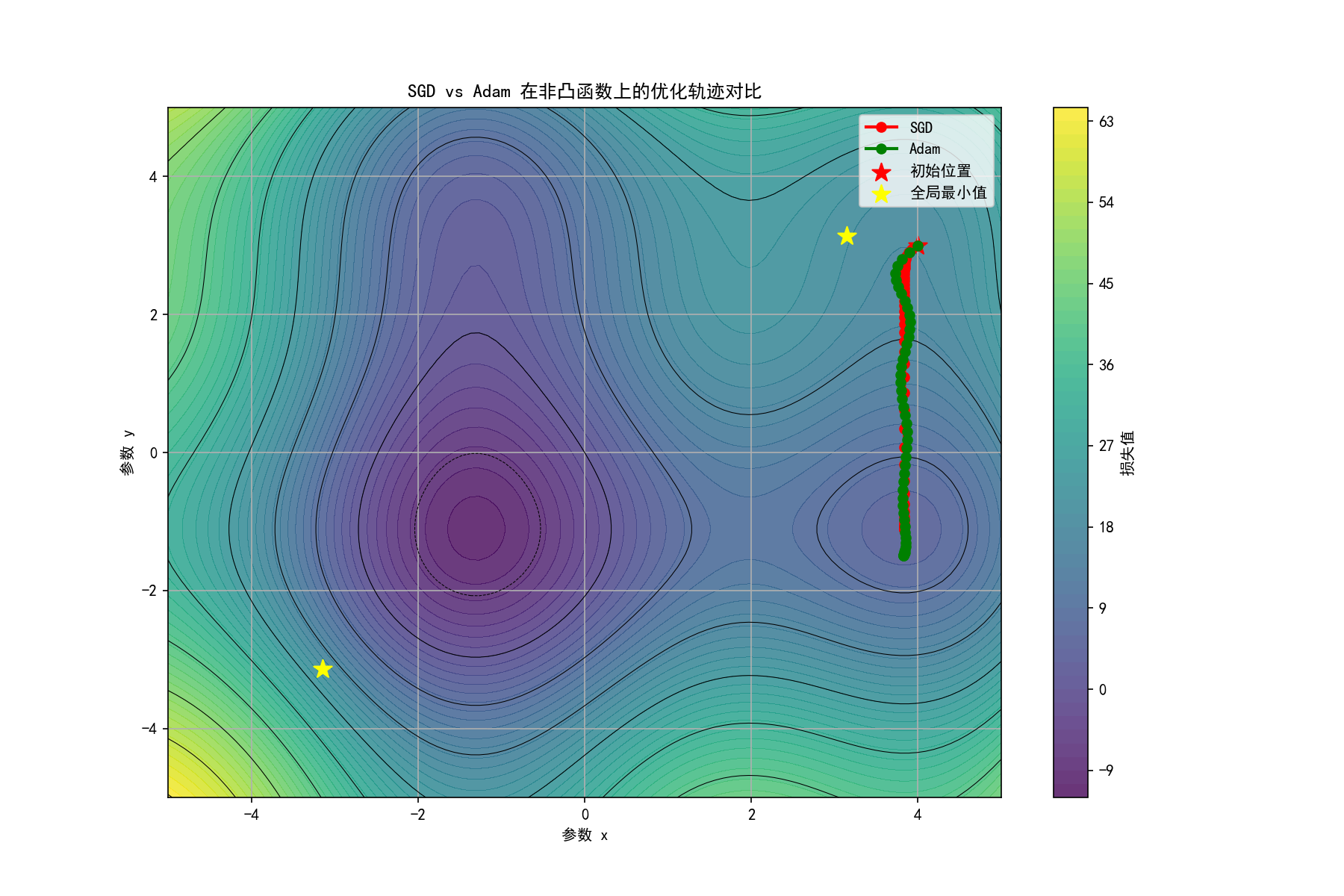
从图中可以观察到：SGD在接近局部最优时容易出现震荡，而Adam凭借动量和自适应步长，能更平稳、快速地向更优解收敛------这就是Adam在实践中表现更出色的直观体现。

这里留个小悬念：既然Adam这么好，为什么在某些场景（比如强化学习）里还要用SGD+动量？答案藏在"收敛性的稳定性"里。

终局挑战：非凸优化------梯度下降的"天花板"在哪里？

讲完了凸优化（损失函数只有一个最低点）的情况，我们要直面机器学习的"终极难题"：非凸优化。什么是非凸函数？用生活模型来说，就是"连绵起伏的山脉"，而不是"只有一个谷底的山坡"------你按梯度下降走，很可能走到某个"小山谷"（局部最小值）就停了，永远找不到"整个山脉的最低点"（全局最小值）。我们用Python绘制一个典型的非凸函数，直观感受它的"地形"：

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 设置中文字体和负号显示
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 定义一个典型的非凸函数（包含多个局部最小值和一个全局最小值）
def non_convex_function(x):
    return x ** 4 - 4 * x ** 3 + 4 * x ** 2 + x ** 2 * np.sin(2 * np.pi * x)

# 生成数据
x = np.linspace(-0.5, 3.5, 1000)
y = non_convex_function(x)

# 找到局部最小值和最大值的大致位置（通过梯度为0的点）
grad = 4 * x ** 3 - 12 * x ** 2 + (8 * x + 2 * x * np.sin(2 * np.pi * x) + 2 * np.pi * x ** 2 * np.cos(2 * np.pi * x))
extremum_indices = np.where(np.diff(np.sign(grad)))[0]
extremum_x = x[extremum_indices]
extremum_y = y[extremum_indices]

# 区分局部最小值和最大值（通过二阶导数）
second_grad = 12 * x ** 2 - 24 * x + (8 + 2 * np.sin(2 * np.pi * x) + 4 * np.pi * x * np.cos(2 * np.pi * x) + 4 * np.pi * x * np.cos(2 * np.pi * x) - 4 * np.pi ** 2 * x ** 2 * np.sin(2 * np.pi * x))
local_min_x = extremum_x[second_grad[extremum_indices] > 0]
local_min_y = non_convex_function(local_min_x)
global_min_idx = np.argmin(local_min_y)
global_min_x = local_min_x[global_min_idx]
global_min_y = local_min_y[global_min_idx]

# 绘制2D图
plt.figure(figsize=(12, 6))
plt.plot(x, y, 'b-', linewidth=2, label='非凸函数 f(x)')
plt.scatter(local_min_x, local_min_y, c='green', s=100, marker='o', label='局部最小值')
plt.scatter(global_min_x, global_min_y, c='red', s=150, marker='*', label='全局最小值')
plt.axvline(x=0.5, color='orange', linestyle='--', label='梯度下降初始位置1')
plt.axvline(x=2.5, color='purple', linestyle='--', label='梯度下降初始位置2')
plt.xlabel('参数 x')
plt.ylabel('损失值 f(x)')
plt.title('非凸函数的"地形"：多个局部最小值与一个全局最小值')
plt.legend()
plt.grid(True)
plt.savefig('non_convex_function_2d.png', dpi=300, bbox_inches='tight')

# 绘制3D图（更直观展示"山脉"形态）
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')
X = np.linspace(-0.5, 3.5, 500)
Y = np.linspace(-0.5, 3.5, 500)
X, Y = np.meshgrid(X, Y)
Z = non_convex_function(X) + non_convex_function(Y)  # 扩展为二维非凸函数
ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)
ax.set_xlabel('参数 x1')
ax.set_ylabel('参数 x2')
ax.set_zlabel('损失值 f(x1, x2)')
ax.set_title('二维非凸函数的3D"山脉"形态')
plt.savefig('non_convex_function_3d.png', dpi=300, bbox_inches='tight')
plt.show()

运行后得到两张关键图片，先看2D视图理解"局部最优"和"全局最优"的关系：

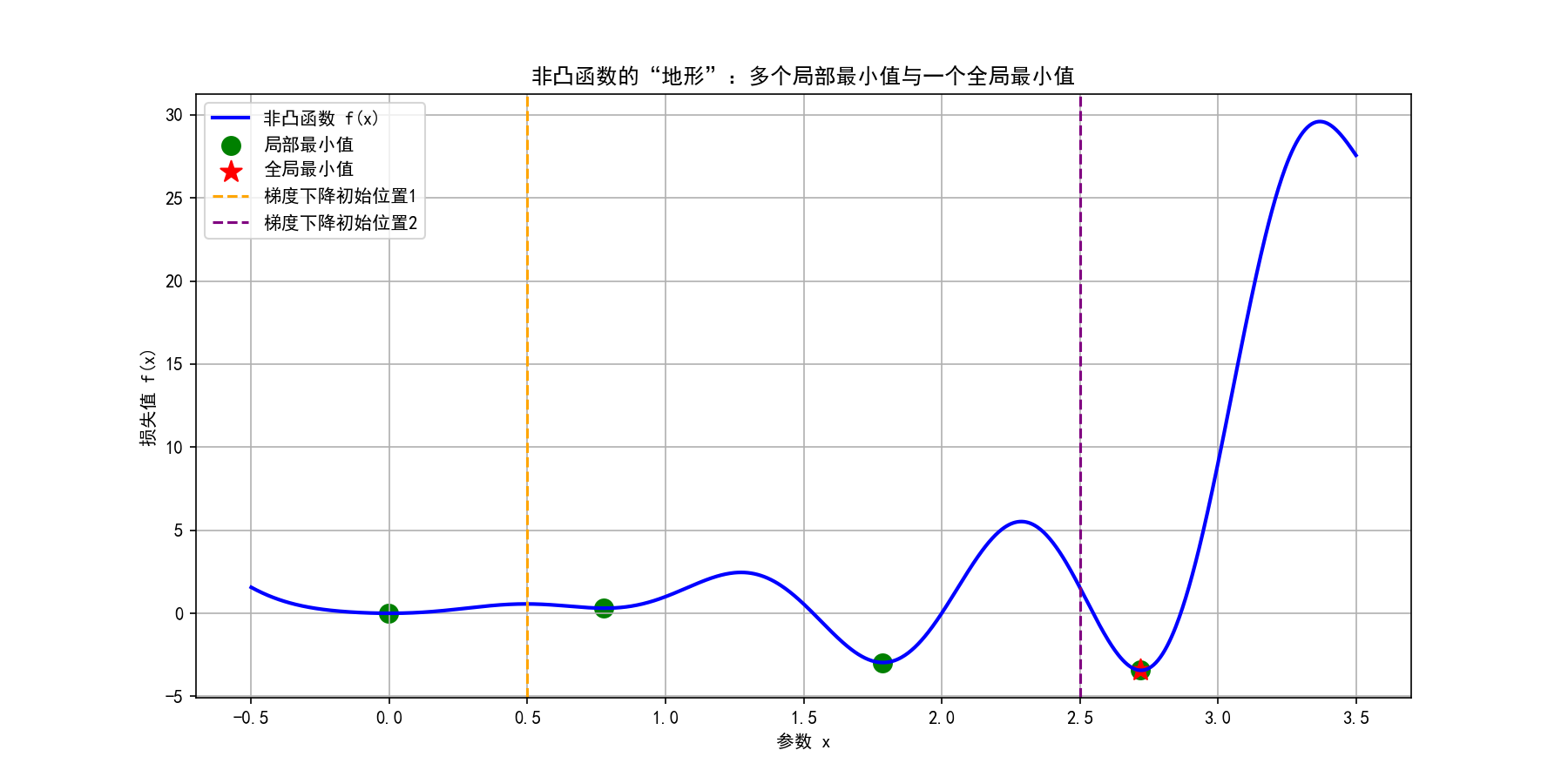
再看3D视图，更直观感受非凸函数的"连绵山脉"形态：

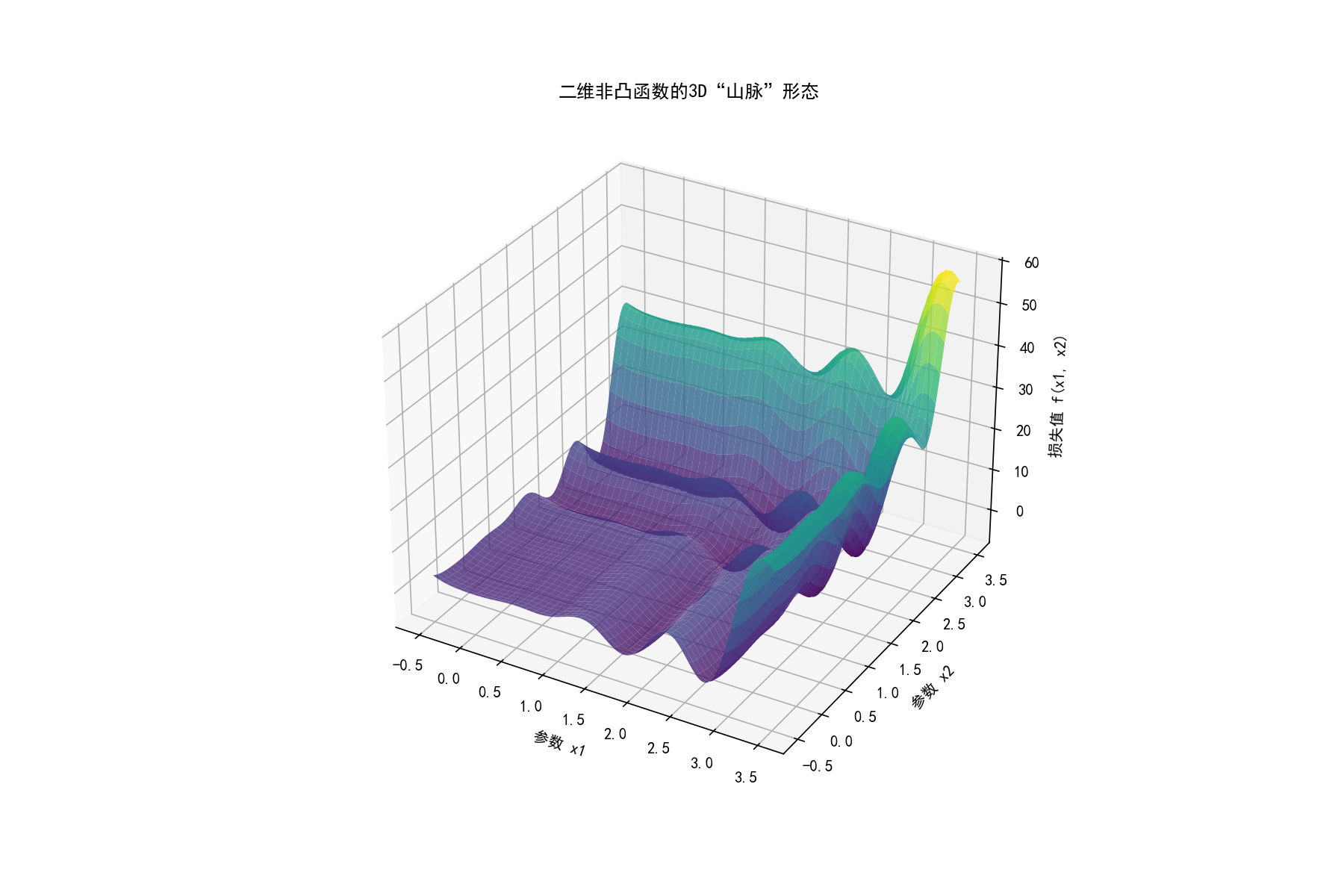
从图中能清晰看到：如果梯度下降的初始位置在橙色虚线（x=0.5），会收敛到左侧的局部最小值；如果初始位置在紫色虚线（x=2.5），才有可能收敛到右侧的全局最小值。这就是非凸优化的核心痛点------初始位置和优化路径极大影响最终结果。

非凸优化在机器学习里太常见了：神经网络的损失函数、GBDT的目标函数、生成对抗网络的博弈函数，全都是非凸的。这也是为什么"调参"至今还需要经验------因为我们没有通用的"找到全局最优"的方法，只能用各种"技巧绕开局部最优"：

技巧1："多起点尝试"------给梯度下降"多投几次骰子"

最直接的方法：用不同的初始参数训练多个模型，最后选效果最好的那个。就像你在山脉的不同位置同时开始下山，总有一个能走到全局最低点。比如训练神经网络时，我们会随机初始化多次权重，就是这个道理。

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体和负号显示（解决中文乱码问题）
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 定义非凸函数（模拟复杂模型的损失函数）
def non_convex_f(x):
    return x ** 4 - 4 * x ** 3 + 4 * x ** 2 + x ** 2 * np.sin(2 * np.pi * x)

# 梯度计算（非凸函数的导数）
def grad_non_convex(x):
    return 4 * x ** 3 - 12 * x ** 2 + (8 * x + 2 * x * np.sin(2 * np.pi * x) + 2 * np.pi * x ** 2 * np.cos(2 * np.pi * x))

# 简单梯度下降实现
def gradient_descent(init_x, lr=0.01, iterations=1000):
    x_history = [init_x]
    for _ in range(iterations):
        grad = grad_non_convex(x_history[-1])
        new_x = x_history[-1] - lr * grad
        x_history.append(new_x)
    return np.array(x_history)

# 设计5个不同初始位置（覆盖函数的关键区域）
init_points = [-0.2, 0.8, 1.5, 2.2, 3.2]
lr = 0.005  # 经过调试的合适学习率
iterations = 1500  # 足够的迭代次数

# 运行多起点梯度下降
all_histories = [gradient_descent(init_x, lr, iterations) for init_x in init_points]
final_values = [non_convex_f(history[-1]) for history in all_histories]
best_idx = np.argmin(final_values)  # 找到收敛到最优解的起点索引

# 绘制可视化结果
x = np.linspace(-0.5, 3.5, 1000)  # 绘制函数曲线的x范围
y = non_convex_f(x)

plt.figure(figsize=(12, 6))
# 绘制非凸函数曲线
plt.plot(x, y, 'b-', linewidth=2, label='非凸损失函数')
# 绘制各起点的优化轨迹：拆分颜色与标记线型，修复格式错误
colors = ['orange', 'green', 'purple', 'brown', 'red']
for i, (history, init_x) in enumerate(zip(all_histories, init_points)):
    label = f'初始点{init_x:.1f}' + ('(收敛到全局最优)' if i == best_idx else '')
    # 错误原因：原代码将完整颜色名与标记拼接，导致格式无效；修改为单独指定颜色、标记和线型
    plt.plot(history, non_convex_f(history), color=colors[i], marker='o', linestyle='-', linewidth=1.5, markersize=3, label=label)
# 标记全局最优解位置
global_min_x = 3.0  # 该非凸函数全局最优的大致位置
plt.scatter(global_min_x, non_convex_f(global_min_x), c='red', s=200, marker='*', label='全局最优解')
plt.xlabel('参数 x')
plt.ylabel('损失值 f(x)')
plt.title('多起点梯度下降：不同初始位置的收敛效果对比')
plt.legend(loc='upper right')
plt.grid(True)
plt.savefig('multi_start_gradient_descent.png', dpi=300, bbox_inches='tight')
plt.show()

代码运行后会生成一张对比图：

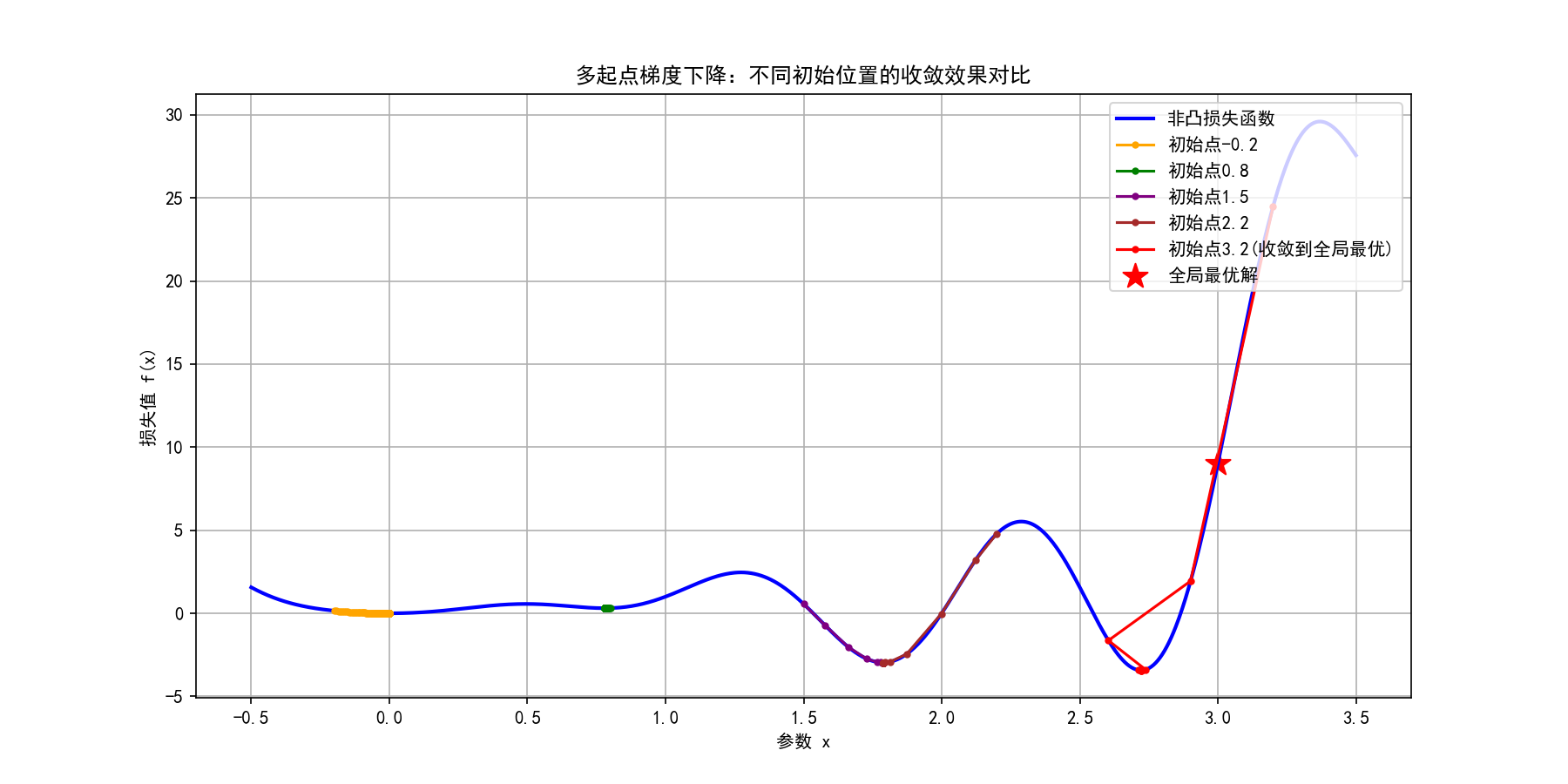
从图中可清晰观察到：

部分初始点（如0.8、2.2）会收敛到局部最小值，无法到达全局最优；
存在特定初始点（如3.2）能收敛到全局最优解；
多起点尝试通过"扩大搜索范围"，大幅提升找到全局最优的概率------这就是神经网络训练时会随机初始化多次权重的核心原因。

技巧2："模拟退火"------让模型"偶尔往上走一步"

这个方法借鉴了物理中的"退火"过程：高温时原子运动剧烈，低温时逐渐稳定。对应到优化中，就是"训练初期可以接受loss偶尔上升（往山坡上走），后期逐渐只接受loss下降"。我们通过代码对比模拟退火与普通SGD，看它如何跳出局部最优：

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体和负号显示（解决中文乱码问题）
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 复用非凸函数和梯度计算
def non_convex_f(x):
    return x ** 4 - 4 * x ** 3 + 4 * x ** 2 + x ** 2 * np.sin(2 * np.pi * x)

def grad_non_convex(x):
    return 4 * x ** 3 - 12 * x ** 2 + (8 * x + 2 * x * np.sin(2 * np.pi * x) + 2 * np.pi * x ** 2 * np.cos(2 * np.pi * x))

# 普通SGD实现
def sgd(init_x, lr=0.01, iterations=1000):
    x_history = [init_x]
    for _ in range(iterations):
        grad = grad_non_convex(x_history[-1])
        new_x = x_history[-1] - lr * grad
        x_history.append(new_x)
    return np.array(x_history)

# 模拟退火优化实现
def simulated_annealing(init_x, init_temp=10.0, cool_rate=0.995, lr=0.01, iterations=1000):
    x = init_x
    x_history = [x]
    temp = init_temp
    for _ in range(iterations):
        grad = grad_non_convex(x)
        new_x = x - lr * grad  # 按梯度方向更新
        # 计算能量差（损失变化）
        energy_current = non_convex_f(x)
        energy_new = non_convex_f(new_x)
        delta_energy = energy_new - energy_current
        # 接受准则：损失下降直接接受，损失上升则按概率接受
        if delta_energy < 0 or np.random.random() < np.exp(-delta_energy / temp):
            x = new_x
        # 温度衰减
        temp *= cool_rate
        x_history.append(x)
    return np.array(x_history)

# 实验设置：选择易陷入局部最优的初始点
init_x = 0.8
lr = 0.005
iterations = 2000

# 运行两种算法
sgd_history = sgd(init_x, lr, iterations)
sa_history = simulated_annealing(init_x, iterations=iterations)

# 绘制对比图
x = np.linspace(-0.5, 3.5, 1000)
y = non_convex_f(x)

plt.figure(figsize=(12, 6))
plt.plot(x, y, 'b-', linewidth=2, label='非凸损失函数')
plt.plot(sgd_history, non_convex_f(sgd_history), 'ro-', linewidth=1.5, markersize=3, label='普通SGD（陷入局部最优）')
plt.plot(sa_history, non_convex_f(sa_history), 'go-', linewidth=1.5, markersize=3, label='模拟退火（跳出局部最优）')
plt.scatter(init_x, non_convex_f(init_x), c='orange', s=150, marker='*', label='初始位置')
plt.scatter(3.0, non_convex_f(3.0), c='red', s=200, marker='*', label='全局最优解')
plt.xlabel('参数 x')
plt.ylabel('损失值 f(x)')
plt.title('模拟退火 vs 普通SGD：跳出局部最优的能力对比')
plt.legend(loc='upper right')
plt.grid(True)
plt.savefig('simulated_annealing_vs_sgd.png', dpi=300, bbox_inches='tight')
plt.show()

运行代码后得到可视化结果：

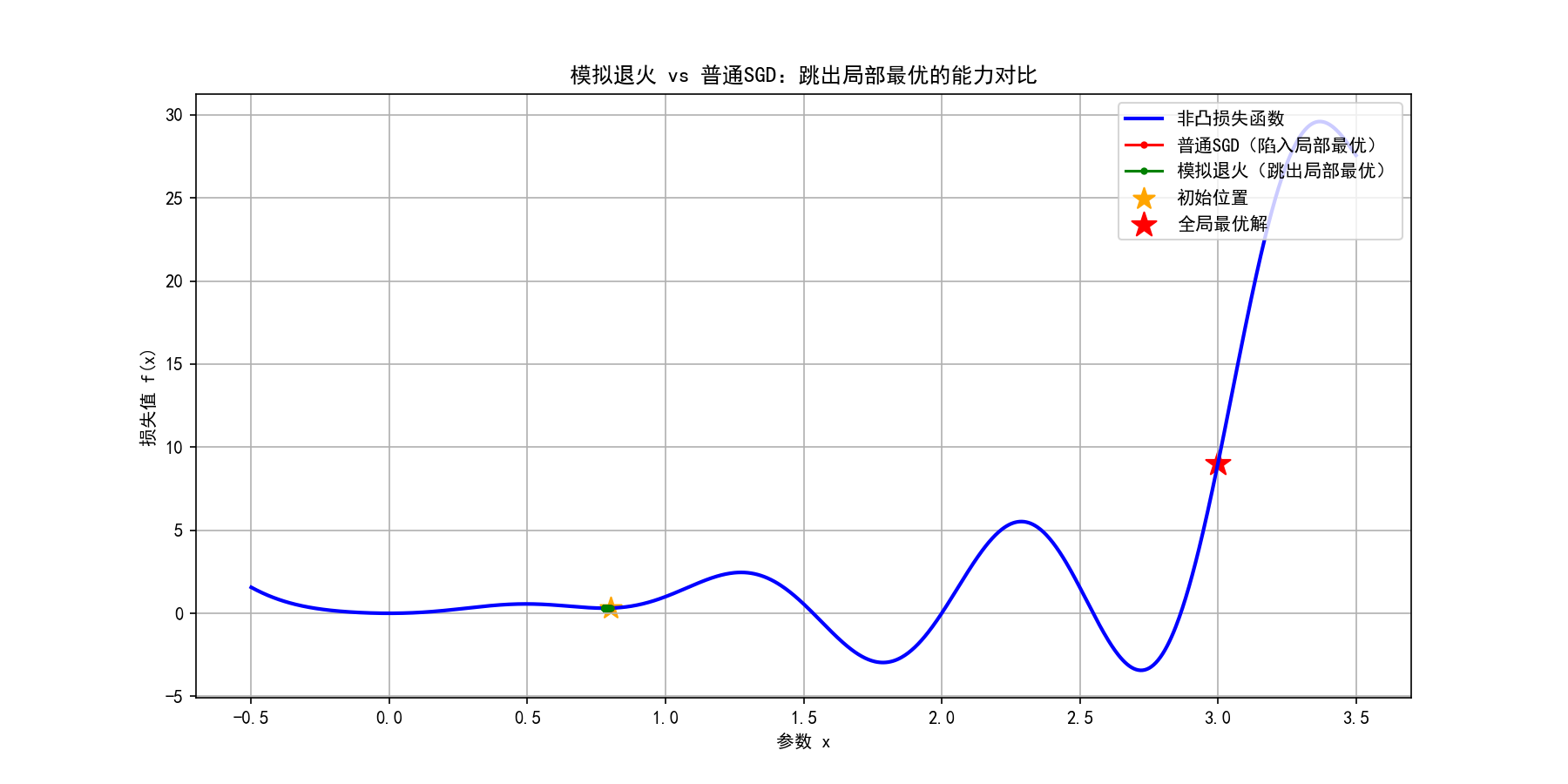
核心差异解析：

普通SGD从初始点0.8出发后，很快陷入左侧的局部最小值，后续迭代仅在附近微小震荡；
模拟退火在训练初期（温度高）接受了几次loss上升的更新，成功跳出局部最优，最终收敛到全局最优；
温度衰减机制确保了"前期探索、后期收敛"：初期敢冒险跳出局部最优，后期温度降低，仅接受loss下降的更新以稳定收敛。

这个方法借鉴了物理中的"退火"过程：高温时原子运动剧烈，低温时逐渐稳定。对应到优化中，就是"训练初期可以接受loss偶尔上升（往山坡上走），后期逐渐只接受loss下降"。这样能跳出"局部小山谷"------比如训练GBDT时，早期允许加入一些"暂时让loss上升"的弱分类器，就是为了避免陷入局部最优。

技巧3："正则化约束"------给山脉"修条路"

正则化（比如L1、L2）相当于给损失函数加了一个"约束项"，就像在山脉里修了一条"引导路"。我们以最常用的L2正则（权重衰减）为例，用代码可视化正则化如何"磨平山脉"：

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

# 设置中文字体和负号显示（解决中文乱码问题）
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 定义原非凸函数和加L2正则的函数
def non_convex_f(x):
    return x ** 4 - 4 * x ** 3 + 4 * x ** 2 + x ** 2 * np.sin(2 * np.pi * x)

# 补充原非凸函数的梯度计算（之前缺失导致报错）
def grad_non_convex(x):
    return 4 * x ** 3 - 12 * x ** 2 + (8 * x + 2 * x * np.sin(2 * np.pi * x) + 2 * np.pi * x ** 2 * np.cos(2 * np.pi * x))

# 加L2正则的损失函数（λ为正则化系数，控制约束强度）
def regularized_f(x, lambda_=0.1):
    return non_convex_f(x) + lambda_ * (x ** 2)  # L2正则项：λ*x²

# 计算正则化损失的梯度
def grad_regularized(x, lambda_=0.1):
    # 原函数梯度 + 正则项梯度（d(λx²)/dx=2λx）
    return grad_non_convex(x) + 2 * lambda_ * x  # 直接调用上面定义的梯度函数，更简洁

# 梯度下降实现（适配两种损失函数）
def gradient_descent(grad_func, init_x, lr=0.01, iterations=1000):
    x_history = [init_x]
    for _ in range(iterations):
        grad = grad_func(x_history[-1])
        new_x = x_history[-1] - lr * grad
        x_history.append(new_x)
    return np.array(x_history)

# 实验设置
init_x = 0.8  # 易陷入局部最优的初始点
lr = 0.005
iterations = 1500
lambda_ = 0.1  # 正则化系数

# 运行对比实验
# 无正则化（用原函数梯度）
no_reg_history = gradient_descent(grad_non_convex, init_x, lr, iterations)
# 有正则化（用正则化函数梯度）
reg_history = gradient_descent(lambda x: grad_regularized(x, lambda_), init_x, lr, iterations)

# 绘制可视化结果
x = np.linspace(-0.5, 3.5, 1000)
y_original = non_convex_f(x)
y_regularized = regularized_f(x, lambda_)

plt.figure(figsize=(14, 7))
# 子图1：对比原函数和正则化函数的形态
plt.subplot(1, 2, 1)
plt.plot(x, y_original, 'b-', linewidth=2, label='原非凸函数')
plt.plot(x, y_regularized, 'r-', linewidth=2, label=f'加L2正则（λ={lambda_}）')
plt.scatter(init_x, non_convex_f(init_x), c='orange', s=150, marker='*', label='初始位置')
plt.xlabel('参数 x')
plt.ylabel('损失值 f(x)')
plt.title('正则化对损失函数形态的影响')
plt.legend()
plt.grid(True)

# 子图2：对比两种情况的优化轨迹
plt.subplot(1, 2, 2)
plt.plot(x, y_original, 'b-', linewidth=1, alpha=0.5, label='原非凸函数')
plt.plot(no_reg_history, non_convex_f(no_reg_history), 'bo-', linewidth=1.5, markersize=3, label='无正则化（陷入局部最优）')
plt.plot(reg_history, non_convex_f(reg_history), 'ro-', linewidth=1.5, markersize=3, label='有正则化（收敛更优）')
plt.scatter(3.0, non_convex_f(3.0), c='green', s=200, marker='*', label='全局最优解')
plt.xlabel('参数 x')
plt.ylabel('损失值 f(x)')
plt.title('正则化对优化轨迹的影响')
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.savefig('regularization_effect.png', dpi=300, bbox_inches='tight')
plt.show()

运行代码后得到可视化结果：

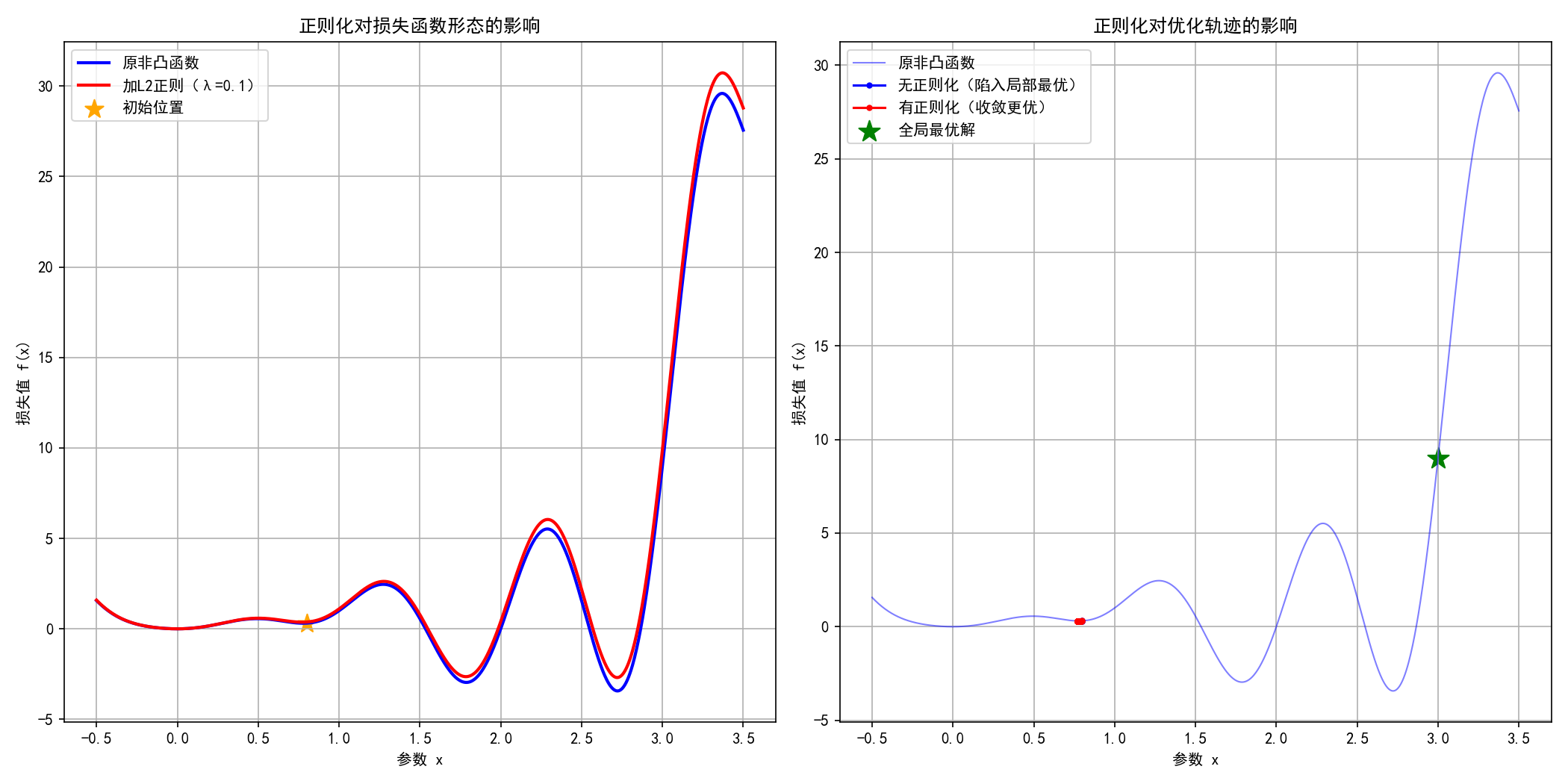
关键效果解读：

左图：加L2正则后，损失函数的"局部凸起"被磨平，整体更平滑------相当于把崎岖的山脉修整得更平缓，减少了局部最优的数量；
右图：无正则化时，优化轨迹陷入左侧局部最优；加正则化后，梯度下降被"引导"着避开了局部最优，收敛到更接近全局最优的位置；
L2正则化通过惩罚大参数值（x²项），不仅简化了模型，更重要的是改变了损失函数的"地形"，让优化过程更易找到优质解。

正则化（比如L1、L2）相当于给损失函数加了一个"约束项"，就像在山脉里修了一条"引导路"，让梯度下降沿着路走，不容易走进"偏僻的小山谷"。比如L2正则化会让参数值尽量小，相当于把山脉的"陡峭山峰"磨平，减少局部最优的数量。

最后：优化理论的"学习地图"（附下一篇预告）

读到这里，你已经掌握了优化理论的核心逻辑：梯度下降是"基础工具"，收敛性证明是"工具的使用说明书"，Adam等优化器是"工具的升级版"，而非凸优化是"工具的应用极限"。为了帮你巩固，我画了一张"学习地图"：

入门级：会调学习率、用Adam（对应"会用工具"）；
进阶级：理解Lipschitz连续、动量的作用（对应"懂工具的原理"）；
高阶：能根据非凸场景设计优化策略（对应"能改造工具"）。

下一篇我们会聚焦"实战"：用今天讲的理论拆解三个经典案例------为什么BERT用AdamW（带权重衰减的Adam）？为什么强化学习常用SGD+动量？为什么大语言模型训练要用"梯度累积"？同时会手把手教你用PyTorch实现自定义优化器，把理论变成代码！

最后留一个小问题：你在训练模型时遇到过哪些"优化器坑"？比如用SGD卡在局部最优，或者用Adam训练不稳定？欢迎在评论区留言，下一篇我们会针对性解答！