《数字图像处理》第 3 章 - 灰度变换与空间滤波

引言

在数字图像处理领域，灰度变换与空间滤波是图像增强 的核心手段，也是入门数字图像处理的关键知识点。灰度变换通过直接修改像素灰度值实现对比度调整、亮度校正等效果；空间滤波则利用邻域像素的运算实现图像平滑、锐化等增强操作。本章将从基础概念到实战代码，全方位拆解灰度变换与空间滤波的核心知识点，结合可视化对比和可直接运行的 Python 代码，让你彻底吃透这部分内容。

学习目标

理解灰度变换与空间滤波的基本原理和应用场景；
掌握常用灰度变换函数（反转、对数、伽马、分段线性）的实现与效果；
精通直方图处理（均衡化、匹配、局部处理）的算法逻辑和代码实现；
掌握空间滤波的核心原理（相关、卷积），能自主构建滤波器核；
实现平滑 / 锐化滤波器，并理解低通、高通、带阻 / 带通滤波器的应用；
学会组合多种空间增强方法解决实际图像增强问题。

3.1 背景

3.1.1 灰度变换和空间滤波基础

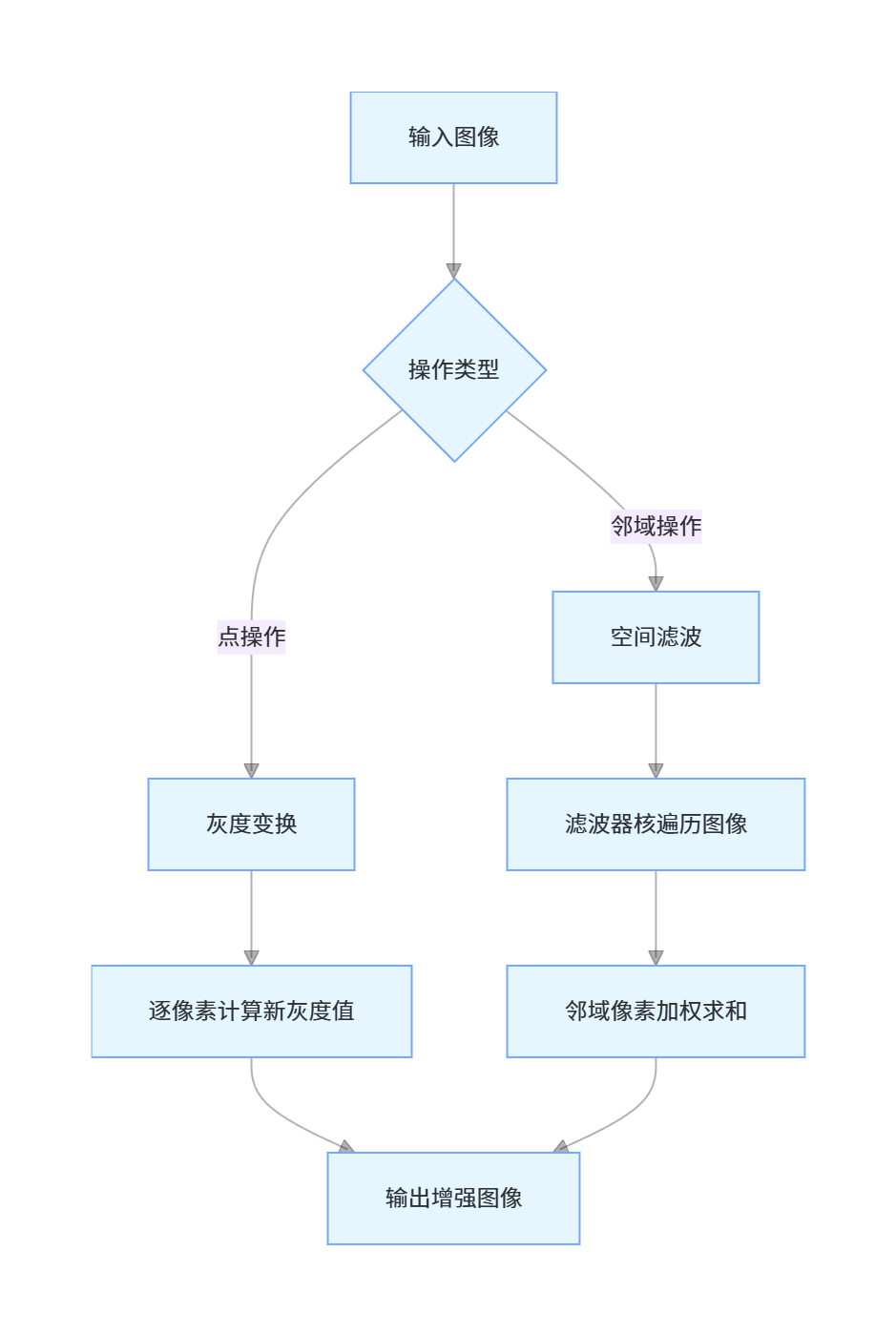
灰度变换是点操作 （Pixel-wise Operation），即每个像素的输出仅由该像素的输入值决定，核心是修改像素的灰度值分布；空间滤波是邻域操作（Neighborhood Operation），即每个像素的输出由该像素及其邻域内的像素共同决定，核心是利用滤波器核（卷积核）对图像进行卷积 / 相关运算。

3.1.2 关于本章中例子的说明

本章所有代码基于 Python 实现，依赖库包括：numpy （数值计算）、cv2 （图像读取 / 处理）、matplotlib （可视化）、skimage（辅助直方图处理）。所有案例使用经典测试图像（如 lena、灰度图），代码可直接运行，运行前需确保安装依赖：

复制代码

pip install numpy opencv-python matplotlib scikit-image

3.2 一些基本的灰度变换函数

核心原理

灰度变换的通用形式为：s = T(r)，其中r是原始像素灰度值，s是变换后的灰度值，T是变换函数。

完整代码实现

复制代码

import numpy as np
import cv2
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']  # 黑体
plt.rcParams['axes.unicode_minus'] = False    # 解决负号显示问题

# 读取图像（转为灰度图）
img = cv2.imread('lena.jpg', cv2.IMREAD_GRAYSCALE)
if img is None:
    raise ValueError("请确保lena.jpg文件在当前目录下，或替换为其他灰度图像路径")

# ---------------------- 3.2.1 图像反转 ----------------------
# 原理：s = L - 1 - r，L为灰度级（通常256）
def invert_image(img):
    return 255 - img

img_invert = invert_image(img)

# ---------------------- 3.2.2 对数变换 ----------------------
# 原理：s = c * log(1 + r)，c为归一化系数
def log_transform(img):
    # 归一化到[0,1]避免数值溢出
    img_normalized = img / 255.0
    # 计算对数变换，加1避免log(0)
    log_img = np.log1p(img_normalized)
    # 归一化回[0,255]
    log_img = (log_img / np.max(log_img)) * 255
    return log_img.astype(np.uint8)

img_log = log_transform(img)

# ---------------------- 3.2.3 幂律（伽马）变换 ----------------------
# 原理：s = c * r^γ，c为归一化系数
def gamma_transform(img, gamma=1.0):
    img_normalized = img / 255.0
    gamma_img = np.power(img_normalized, gamma)
    gamma_img = (gamma_img / np.max(gamma_img)) * 255
    return gamma_img.astype(np.uint8)

# 对比不同gamma值的效果
img_gamma_05 = gamma_transform(img, 0.5)  # 增强亮部
img_gamma_2 = gamma_transform(img, 2.0)   # 增强暗部

# ---------------------- 3.2.4 分段线性变换（对比度拉伸） ----------------------
# 原理：分段线性函数，拉伸指定灰度区间的对比度
def piecewise_linear(img, r1=50, s1=0, r2=200, s2=255):
    # 创建变换映射表
    lut = np.zeros(256, dtype=np.uint8)
    for r in range(256):
        if r < r1:
            lut[r] = (s1 / r1) * r if r1 != 0 else 0
        elif r > r2:
            lut[r] = s2 + ((255 - s2) / (255 - r2)) * (r - r2) if r2 != 255 else 255
        else:
            lut[r] = s1 + ((s2 - s1) / (r2 - r1)) * (r - r1)
    # 应用映射表
    return cv2.LUT(img, lut)

img_piecewise = piecewise_linear(img)

# ---------------------- 可视化所有效果 ----------------------
plt.figure(figsize=(16, 12))

# 原始图像
plt.subplot(3, 3, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

# 图像反转
plt.subplot(3, 3, 2)
plt.imshow(img_invert, cmap='gray')
plt.title('图像反转')
plt.axis('off')

# 对数变换
plt.subplot(3, 3, 3)
plt.imshow(img_log, cmap='gray')
plt.title('对数变换')
plt.axis('off')

# 伽马变换（gamma=0.5）
plt.subplot(3, 3, 4)
plt.imshow(img_gamma_05, cmap='gray')
plt.title('伽马变换 (γ=0.5)')
plt.axis('off')

# 伽马变换（gamma=2.0）
plt.subplot(3, 3, 5)
plt.imshow(img_gamma_2, cmap='gray')
plt.title('伽马变换 (γ=2.0)')
plt.axis('off')

# 分段线性变换
plt.subplot(3, 3, 6)
plt.imshow(img_piecewise, cmap='gray')
plt.title('分段线性变换（对比度拉伸）')
plt.axis('off')

# 原始图像直方图
plt.subplot(3, 3, 7)
plt.hist(img.ravel(), bins=256, range=[0,255])
plt.title('原始图像直方图')
plt.xlabel('灰度值')
plt.ylabel('像素数')

# 伽马变换(γ=0.5)直方图
plt.subplot(3, 3, 8)
plt.hist(img_gamma_05.ravel(), bins=256, range=[0,255])
plt.title('伽马变换(γ=0.5)直方图')
plt.xlabel('灰度值')
plt.ylabel('像素数')

# 分段线性变换直方图
plt.subplot(3, 3, 9)
plt.hist(img_piecewise.ravel(), bins=256, range=[0,255])
plt.title('分段线性变换直方图')
plt.xlabel('灰度值')
plt.ylabel('像素数')

plt.tight_layout()
plt.show()

效果说明

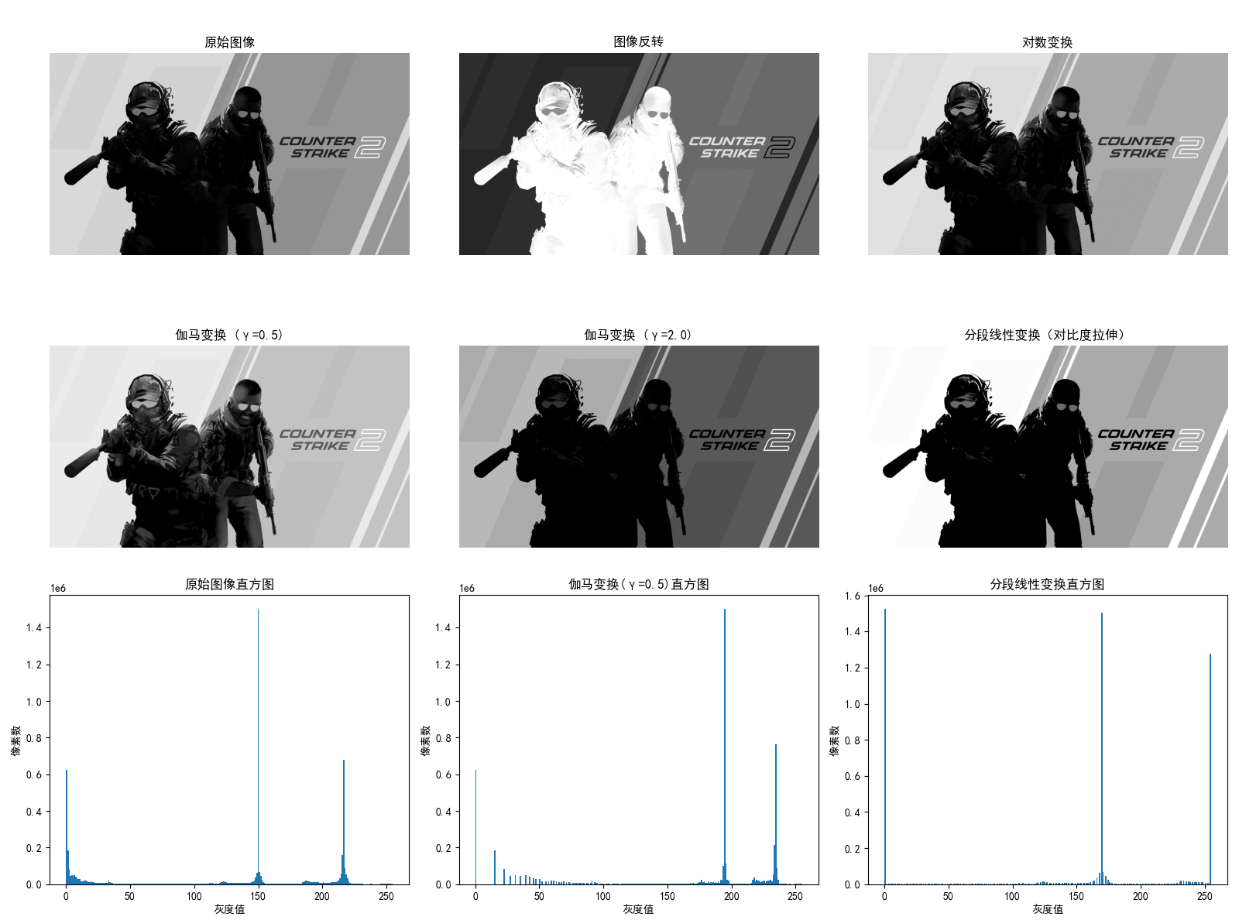
图像反转：适用于增强暗背景下的亮物体（如医学影像）；
对数变换：压缩高灰度值区间，扩展低灰度值区间，适合增强图像暗部细节；
伽马变换：γ<1 增强亮部，γ>1 增强暗部，是调整图像对比度的常用手段；
分段线性变换：可精准拉伸指定灰度区间的对比度，适合修复对比度不足的图像。

3.3 直方图处理

核心原理

图像直方图是灰度值的像素数统计分布，直方图处理通过调整灰度分布实现图像增强。

完整代码实现

复制代码

import numpy as np
import cv2
import matplotlib.pyplot as plt
from skimage import exposure

# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 读取低对比度灰度图像（效果更明显）
img = cv2.imread('low_contrast.jpg', cv2.IMREAD_GRAYSCALE)
if img is None:
    # 若没有低对比度图像，用lena模拟
    img = cv2.imread('lena.jpg', cv2.IMREAD_GRAYSCALE)
    # 降低对比度
    img = cv2.convertScaleAbs(img, alpha=0.5, beta=50)

# ---------------------- 3.3.1 直方图均衡化 ----------------------
# 全局直方图均衡化
img_eq = cv2.equalizeHist(img)
# 自适应（局部）直方图均衡化（3.3.3）
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8,8))
img_clahe = clahe.apply(img)

# ---------------------- 3.3.2 直方图匹配（规定化） ----------------------
# 生成目标直方图（这里用正态分布模拟）
target_hist = np.zeros(256)
mu, sigma = 128, 32
for i in range(256):
    target_hist[i] = np.exp(-((i - mu)**2) / (2 * sigma**2))
target_hist = target_hist / target_hist.sum() * img.size  # 归一化到像素数

# 用skimage实现直方图匹配
img_matched = exposure.match_histograms(img, img_eq, channel_axis=None)

# ---------------------- 3.3.4 直方图计量增强（对比度自适应） ----------------------
# 计算直方图均值和方差
hist = cv2.calcHist([img], [0], None, [256], [0,256])
mean_gray = np.sum(np.arange(256) * hist) / img.size
std_gray = np.sqrt(np.sum(((np.arange(256) - mean_gray)**2) * hist) / img.size)

# 自适应增强：拉伸到均值±2σ
lower = max(0, mean_gray - 2 * std_gray)
upper = min(255, mean_gray + 2 * std_gray)
img_metric = np.clip((img - lower) * 255 / (upper - lower), 0, 255).astype(np.uint8)

# ---------------------- 可视化 ----------------------
plt.figure(figsize=(16, 10))

# 原始图像及直方图
plt.subplot(4, 2, 1)
plt.imshow(img, cmap='gray')
plt.title('原始低对比度图像')
plt.axis('off')

plt.subplot(4, 2, 2)
plt.hist(img.ravel(), bins=256, range=[0,255], alpha=0.7)
plt.title('原始图像直方图')
plt.xlabel('灰度值')
plt.ylabel('像素数')

# 全局均衡化
plt.subplot(4, 2, 3)
plt.imshow(img_eq, cmap='gray')
plt.title('3.3.1 全局直方图均衡化')
plt.axis('off')

plt.subplot(4, 2, 4)
plt.hist(img_eq.ravel(), bins=256, range=[0,255], alpha=0.7)
plt.title('均衡化后直方图')
plt.xlabel('灰度值')
plt.ylabel('像素数')

# 直方图匹配
plt.subplot(4, 2, 5)
plt.imshow(img_matched, cmap='gray')
plt.title('3.3.2 直方图匹配（规定化）')
plt.axis('off')

plt.subplot(4, 2, 6)
plt.hist(img_matched.ravel(), bins=256, range=[0,255], alpha=0.7)
plt.title('匹配后直方图')
plt.xlabel('灰度值')
plt.ylabel('像素数')

# 局部直方图均衡化
plt.subplot(4, 2, 7)
plt.imshow(img_clahe, cmap='gray')
plt.title('3.3.3 局部直方图均衡化（CLAHE）')
plt.axis('off')

# 直方图计量增强
plt.subplot(4, 2, 8)
plt.imshow(img_metric, cmap='gray')
plt.title('3.3.4 直方图计量增强')
plt.axis('off')

plt.tight_layout()
plt.show()

效果说明

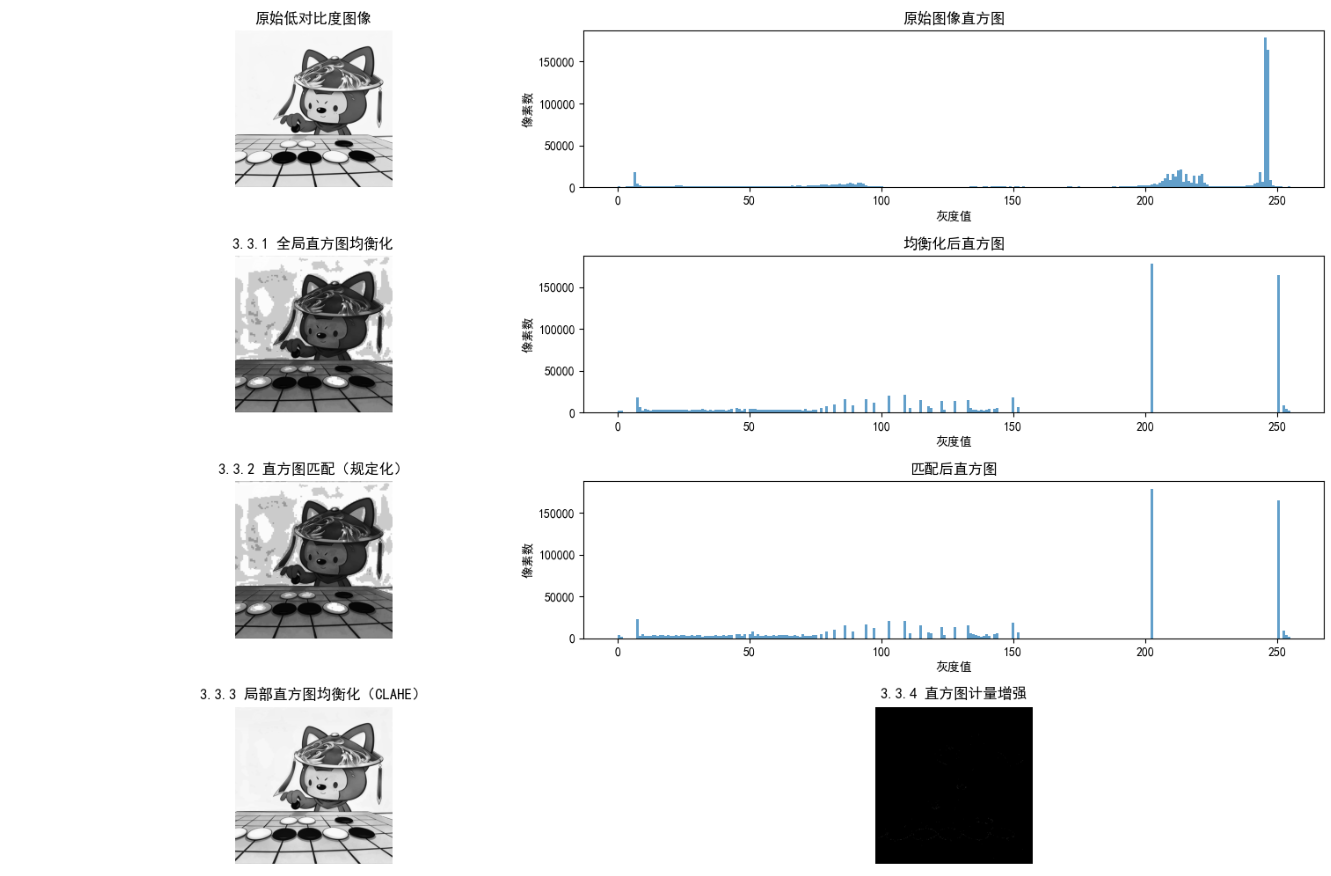
直方图均衡化：全局拉伸灰度分布，提升整体对比度，但可能过度增强噪声；
直方图匹配：将图像直方图匹配到指定分布，精准控制增强效果；
局部直方图处理（CLAHE）：分块均衡化，避免全局均衡化的过增强问题，保留局部细节；
直方图计量增强：基于统计特征（均值、方差）自适应增强，更鲁棒。

3.4 空间滤波基础

核心原理

空间滤波的核心是滤波器核 （Kernel）与图像的相关 / 卷积运算：

相关：核直接滑过图像，对应位置相乘求和；
卷积：核先旋转 180°，再做相关运算。

完整代码实现

复制代码

import numpy as np
import cv2
import matplotlib.pyplot as plt

# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 读取图像
img = cv2.imread('lena.jpg', cv2.IMREAD_GRAYSCALE)

# ---------------------- 3.4.1 线性空间滤波原理 ----------------------
# 自定义线性滤波函数（手动实现，理解原理）
def linear_filter(img, kernel):
    # 获取核大小和图像尺寸
    k_h, k_w = kernel.shape
    img_h, img_w = img.shape
    # 计算填充大小（保持输出尺寸与输入一致）
    pad_h = k_h // 2
    pad_w = k_w // 2
    # 零填充
    img_pad = np.pad(img, ((pad_h, pad_h), (pad_w, pad_w)), mode='constant')
    # 初始化输出图像
    output = np.zeros_like(img, dtype=np.float32)
    
    # 滑窗遍历
    for i in range(img_h):
        for j in range(img_w):
            # 提取邻域
            neighborhood = img_pad[i:i+k_h, j:j+k_w]
            # 加权求和（相关运算）
            output[i, j] = np.sum(neighborhood * kernel)
    
    # 归一化到[0,255]
    output = np.clip(output, 0, 255).astype(np.uint8)
    return output

# ---------------------- 3.4.2 空间相关与卷积对比 ----------------------
# 定义3x3均值核
kernel = np.ones((3,3)) / 9

# 手动实现的相关运算
img_correlate = linear_filter(img, kernel)

# OpenCV的滤波（默认相关）
img_cv_correlate = cv2.filter2D(img, -1, kernel)

# 卷积运算（核旋转180°后相关）
kernel_rot = np.rot90(kernel, 2)  # 旋转180°
img_convolve = linear_filter(img, kernel_rot)

# ---------------------- 3.4.3 可分离滤波器核 ----------------------
# 可分离核：3x3高斯核 = 1x3高斯核 × 3x1高斯核
gauss_1d = np.array([1, 2, 1]) / 4
gauss_2d = np.outer(gauss_1d, gauss_1d)  # 外积生成2D核

# 分离滤波：先行后列
img_sep_1 = cv2.filter2D(img, -1, gauss_1d.reshape(1,3))  # 行滤波
img_sep_2 = cv2.filter2D(img_sep_1, -1, gauss_1d.reshape(3,1))  # 列滤波

# 直接2D滤波
img_2d = cv2.filter2D(img, -1, gauss_2d)

# ---------------------- 3.4.4 空域/频域滤波对比 ----------------------
# 空域高斯滤波
img_spatial = cv2.GaussianBlur(img, (5,5), 1.5)

# 频域高斯滤波（简化版）
# 1. 图像补零到2的幂次
h, w = img.shape
new_h = cv2.getOptimalDFTSize(h)
new_w = cv2.getOptimalDFTSize(w)
img_pad = np.zeros((new_h, new_w), dtype=np.float32)
img_pad[:h, :w] = img / 255.0

# 2. 傅里叶变换
dft = cv2.dft(img_pad, flags=cv2.DFT_COMPLEX_OUTPUT)
dft_shift = np.fft.fftshift(dft)

# 3. 构建频域高斯低通核
crow, ccol = new_h//2, new_w//2
mask = np.zeros((new_h, new_w, 2), dtype=np.float32)
x, y = np.meshgrid(np.arange(new_w), np.arange(new_h))
distance = np.sqrt((x - ccol)**2 + (y - crow)**2)
mask = np.exp(-(distance**2) / (2 * (1.5*2)**2))
mask = np.stack([mask, mask], axis=-1)

# 4. 频域滤波
dft_filtered = dft_shift * mask
dft_ishift = np.fft.ifftshift(dft_filtered)
img_freq = cv2.idft(dft_ishift)
img_freq = cv2.magnitude(img_freq[:, :, 0], img_freq[:, :, 1])
img_freq = (img_freq / np.max(img_freq) * 255).astype(np.uint8)
img_freq = img_freq[:h, :w]  # 裁剪回原尺寸

# ---------------------- 3.4.5 构建空间滤波器核 ----------------------
# 自定义3x3拉普拉斯核
laplacian_kernel = np.array([[0, 1, 0],
                             [1, -4, 1],
                             [0, 1, 0]])
img_laplacian = cv2.filter2D(img, -1, laplacian_kernel)

# ---------------------- 可视化 ----------------------
plt.figure(figsize=(18, 12))

# 相关与卷积
plt.subplot(3, 4, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

plt.subplot(3, 4, 2)
plt.imshow(img_correlate, cmap='gray')
plt.title('3.4.2 手动相关运算')
plt.axis('off')

plt.subplot(3, 4, 3)
plt.imshow(img_convolve, cmap='gray')
plt.title('3.4.2 手动卷积运算')
plt.axis('off')

plt.subplot(3, 4, 4)
plt.imshow(img_cv_correlate, cmap='gray')
plt.title('OpenCV相关运算')
plt.axis('off')

# 可分离核
plt.subplot(3, 4, 5)
plt.imshow(img_sep_2, cmap='gray')
plt.title('3.4.3 可分离核滤波（分离实现）')
plt.axis('off')

plt.subplot(3, 4, 6)
plt.imshow(img_2d, cmap='gray')
plt.title('3.4.3 可分离核滤波（2D实现）')
plt.axis('off')

# 空域/频域对比
plt.subplot(3, 4, 7)
plt.imshow(img_spatial, cmap='gray')
plt.title('3.4.4 空域高斯滤波')
plt.axis('off')

plt.subplot(3, 4, 8)
plt.imshow(img_freq, cmap='gray')
plt.title('3.4.4 频域高斯滤波')
plt.axis('off')

# 自定义核
plt.subplot(3, 4, 9)
plt.imshow(img_laplacian, cmap='gray')
plt.title('3.4.5 自定义拉普拉斯核滤波')
plt.axis('off')

plt.tight_layout()
plt.show()

核心知识点总结

相关 vs 卷积：线性滤波中，若核是对称的（如均值、高斯），相关和卷积结果一致；非对称核（如 Sobel）需注意区别；
可分离核：将 2D 核分解为两个 1D 核，可将时间复杂度从 O (n²) 降为 O (n)，提升效率；
空域 vs 频域滤波：空域直观、易实现，频域适合复杂滤波（如带阻 / 带通），但计算成本更高。

3.5 平滑（低通）空间滤波器

核心原理

低通滤波器通过抑制高频分量（边缘、噪声）实现图像平滑，分为线性（均值、高斯）和非线性（中值、最大值、最小值）两类。

完整代码实现

复制代码

import numpy as np
import cv2
import matplotlib.pyplot as plt

# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 读取含噪声的图像（添加椒盐噪声）
img = cv2.imread('lena.jpg', cv2.IMREAD_GRAYSCALE)
# 添加椒盐噪声
def add_salt_pepper_noise(img, prob=0.05):
    output = np.copy(img)
    # 盐噪声（白）
    salt = np.random.rand(*img.shape) < prob/2
    output[salt] = 255
    # 椒噪声（黑）
    pepper = np.random.rand(*img.shape) < prob/2
    output[pepper] = 0
    return output

img_noise = add_salt_pepper_noise(img)

# ---------------------- 3.5.1 盒式滤波器核（均值滤波） ----------------------
# 3x3盒式核
kernel_box = np.ones((3,3)) / 9
img_box = cv2.filter2D(img_noise, -1, kernel_box)
# 5x5均值滤波（OpenCV内置）
img_blur = cv2.blur(img_noise, (5,5))

# ---------------------- 3.5.2 低通高斯滤波器核 ----------------------
# 3x3高斯滤波（σ=1）
img_gauss = cv2.GaussianBlur(img_noise, (3,3), 1)
# 5x5高斯滤波（σ=2）
img_gauss_large = cv2.GaussianBlur(img_noise, (5,5), 2)

# ---------------------- 3.5.3 统计排序（非线性）滤波器 ----------------------
# 中值滤波（最适合椒盐噪声）
img_median = cv2.medianBlur(img_noise, 3)
# 最大值滤波（去除椒噪声）
img_max = cv2.dilate(img_noise, np.ones((3,3)))
# 最小值滤波（去除盐噪声）
img_min = cv2.erode(img_noise, np.ones((3,3)))

# ---------------------- 可视化 ----------------------
plt.figure(figsize=(16, 12))

# 原始噪声图像
plt.subplot(3, 4, 1)
plt.imshow(img_noise, cmap='gray')
plt.title('含椒盐噪声的原始图像')
plt.axis('off')

# 盒式滤波器
plt.subplot(3, 4, 2)
plt.imshow(img_box, cmap='gray')
plt.title('3.5.1 3x3盒式滤波器')
plt.axis('off')

plt.subplot(3, 4, 3)
plt.imshow(img_blur, cmap='gray')
plt.title('3.5.1 5x5均值滤波')
plt.axis('off')

# 高斯滤波器
plt.subplot(3, 4, 4)
plt.imshow(img_gauss, cmap='gray')
plt.title('3.5.2 3x3高斯滤波（σ=1）')
plt.axis('off')

plt.subplot(3, 4, 5)
plt.imshow(img_gauss_large, cmap='gray')
plt.title('3.5.2 5x5高斯滤波（σ=2）')
plt.axis('off')

# 统计排序滤波器
plt.subplot(3, 4, 6)
plt.imshow(img_median, cmap='gray')
plt.title('3.5.3 中值滤波（3x3）')
plt.axis('off')

plt.subplot(3, 4, 7)
plt.imshow(img_max, cmap='gray')
plt.title('3.5.3 最大值滤波（去椒噪声）')
plt.axis('off')

plt.subplot(3, 4, 8)
plt.imshow(img_min, cmap='gray')
plt.title('3.5.3 最小值滤波（去盐噪声）')
plt.axis('off')

# 对比：原始无噪声图像
plt.subplot(3, 4, 9)
plt.imshow(img, cmap='gray')
plt.title('原始无噪声图像')
plt.axis('off')

plt.tight_layout()
plt.show()

效果说明

盒式滤波器：简单但易模糊边缘，核越大模糊越严重；
高斯滤波器：平滑的同时保留更多边缘细节，σ 越大平滑效果越强；
中值滤波：非线性滤波，是去除椒盐噪声的最优选择，不会产生模糊；
最大值 / 最小值滤波：分别适合去除椒噪声 / 盐噪声，也可用于形态学操作。

3.6 锐化（高通）空间滤波器

核心原理

高通滤波器通过增强高频分量（边缘、细节）实现图像锐化，核心是提取图像的梯度 / 二阶导数。

完整代码实现（含效果对比）

复制代码

import numpy as np
import cv2
import matplotlib.pyplot as plt

# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 读取图像
img = cv2.imread('lena.jpg', cv2.IMREAD_GRAYSCALE)
# 先轻微平滑（去噪声），避免锐化放大噪声
img_smooth = cv2.GaussianBlur(img, (3,3), 0.5)

# ---------------------- 3.6.2 拉普拉斯算子（二阶导数） ----------------------
# 4邻域拉普拉斯核
laplacian_4 = np.array([[0, 1, 0],
                        [1, -4, 1],
                        [0, 1, 0]])
# 8邻域拉普拉斯核
laplacian_8 = np.array([[1, 1, 1],
                        [1, -8, 1],
                        [1, 1, 1]])

# 拉普拉斯滤波（提取边缘）
img_lap4 = cv2.filter2D(img_smooth, cv2.CV_64F, laplacian_4)
img_lap8 = cv2.filter2D(img_smooth, cv2.CV_64F, laplacian_8)

# 锐化图像 = 原始图像 - 拉普拉斯图像（增强边缘）
img_sharpen_lap4 = img - img_lap4
img_sharpen_lap8 = img - img_lap8
# 归一化到[0,255]
img_sharpen_lap4 = np.clip(img_sharpen_lap4, 0, 255).astype(np.uint8)
img_sharpen_lap8 = np.clip(img_sharpen_lap8, 0, 255).astype(np.uint8)

# ---------------------- 3.6.3 钝化掩蔽和高提升滤波 ----------------------
# 钝化掩蔽：原始 - 模糊
img_blur = cv2.GaussianBlur(img, (5,5), 1)
mask = img - img_blur
img_unsharp = img + mask  # 钝化掩蔽

# 高提升滤波：原始 + k*mask（k>1）
k = 2
img_high_boost = img + k * mask
img_high_boost = np.clip(img_high_boost, 0, 255).astype(np.uint8)

# ---------------------- 3.6.4 一阶导数锐化（梯度） ----------------------
# Sobel算子（梯度）
# x方向梯度
sobel_x = cv2.Sobel(img_smooth, cv2.CV_64F, 1, 0, ksize=3)
# y方向梯度
sobel_y = cv2.Sobel(img_smooth, cv2.CV_64F, 0, 1, ksize=3)
# 梯度幅值
sobel_mag = np.sqrt(sobel_x**2 + sobel_y**2)
sobel_mag = (sobel_mag / np.max(sobel_mag) * 255).astype(np.uint8)

# Prewitt算子
prewitt_x = np.array([[-1, 0, 1],
                      [-1, 0, 1],
                      [-1, 0, 1]])
prewitt_y = np.array([[-1, -1, -1],
                      [0, 0, 0],
                      [1, 1, 1]])
img_prewitt_x = cv2.filter2D(img_smooth, cv2.CV_64F, prewitt_x)
img_prewitt_y = cv2.filter2D(img_smooth, cv2.CV_64F, prewitt_y)
prewitt_mag = np.sqrt(img_prewitt_x**2 + img_prewitt_y**2)
prewitt_mag = (prewitt_mag / np.max(prewitt_mag) * 255).astype(np.uint8)

# ---------------------- 可视化 ----------------------
plt.figure(figsize=(18, 12))

# 原始图像
plt.subplot(4, 4, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

# 拉普拉斯锐化
plt.subplot(4, 4, 2)
plt.imshow(img_sharpen_lap4, cmap='gray')
plt.title('3.6.2 4邻域拉普拉斯锐化')
plt.axis('off')

plt.subplot(4, 4, 3)
plt.imshow(img_sharpen_lap8, cmap='gray')
plt.title('3.6.2 8邻域拉普拉斯锐化')
plt.axis('off')

# 钝化掩蔽和高提升
plt.subplot(4, 4, 4)
plt.imshow(img_unsharp, cmap='gray')
plt.title('3.6.3 钝化掩蔽')
plt.axis('off')

plt.subplot(4, 4, 5)
plt.imshow(img_high_boost, cmap='gray')
plt.title('3.6.3 高提升滤波（k=2）')
plt.axis('off')

# Sobel梯度
plt.subplot(4, 4, 6)
plt.imshow(sobel_mag, cmap='gray')
plt.title('3.6.4 Sobel梯度幅值')
plt.axis('off')

# Prewitt梯度
plt.subplot(4, 4, 7)
plt.imshow(prewitt_mag, cmap='gray')
plt.title('3.6.4 Prewitt梯度幅值')
plt.axis('off')

# 拉普拉斯边缘
plt.subplot(4, 4, 8)
plt.imshow(np.abs(img_lap4).astype(np.uint8), cmap='gray')
plt.title('4邻域拉普拉斯边缘')
plt.axis('off')

plt.tight_layout()
plt.show()

效果说明

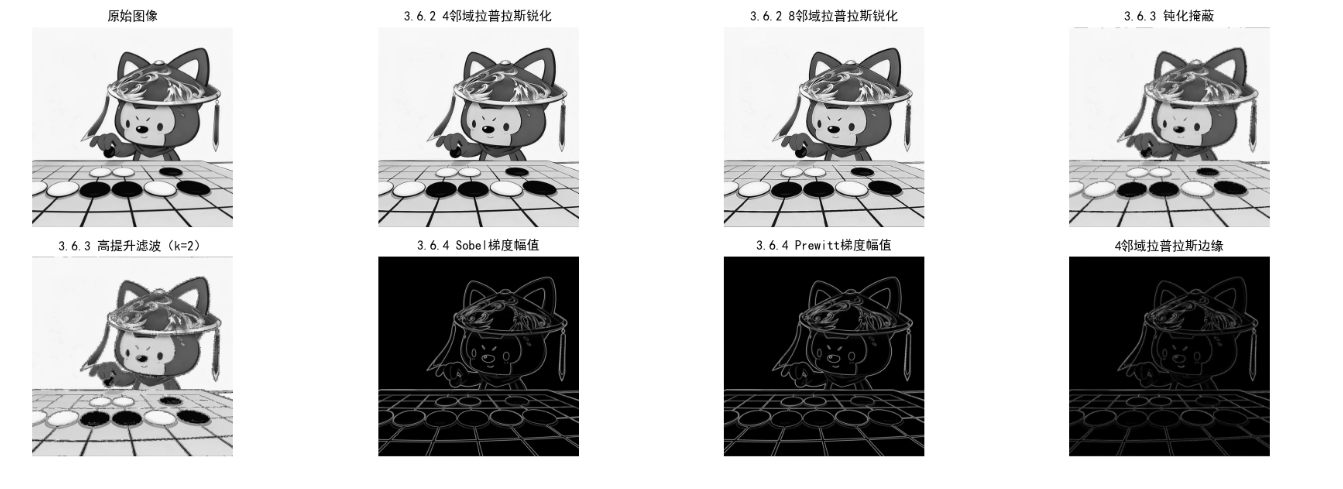
拉普拉斯算子：对噪声敏感，需先平滑；8 邻域比 4 邻域提取的边缘更完整；
钝化掩蔽 / 高提升滤波：实用的锐化方法，k 越大锐化效果越强，但易放大噪声；
梯度算子（Sobel/Prewitt）：Sobel 加入了高斯权重，抗噪声能力更强，是工程中常用的边缘检测算子。

3.7 低通、高通、带阻和带通滤波器

核心原理

低通：保留低频（平滑），抑制高频（边缘 / 噪声）；
高通：保留高频（边缘），抑制低频（背景）；
带阻：抑制指定频率范围（如周期性噪声）；
带通：保留指定频率范围（如提取特定尺度的边缘）。

完整代码实现

复制代码

import numpy as np
import cv2
import matplotlib.pyplot as plt

# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 读取图像
img = cv2.imread('lena.jpg', cv2.IMREAD_GRAYSCALE)
h, w = img.shape

# 傅里叶变换（频域处理）
def dft_process(img):
    # 补零到最优尺寸
    new_h = cv2.getOptimalDFTSize(h)
    new_w = cv2.getOptimalDFTSize(w)
    img_pad = np.zeros((new_h, new_w), dtype=np.float32)
    img_pad[:h, :w] = img / 255.0
    # 傅里叶变换
    dft = cv2.dft(img_pad, flags=cv2.DFT_COMPLEX_OUTPUT)
    return np.fft.fftshift(dft), new_h, new_w

def idft_process(dft_shift, new_h, new_w):
    # 逆傅里叶变换
    dft_ishift = np.fft.ifftshift(dft_shift)
    img_back = cv2.idft(dft_ishift)
    img_back = cv2.magnitude(img_back[:, :, 0], img_back[:, :, 1])
    # 归一化并裁剪
    img_back = (img_back / np.max(img_back) * 255).astype(np.uint8)
    return img_back[:h, :w]

# 生成频域掩码
dft_shift, new_h, new_w = dft_process(img)
crow, ccol = new_h//2, new_w//2
x, y = np.meshgrid(np.arange(new_w), np.arange(new_h))
distance = np.sqrt((x - ccol)**2 + (y - crow)**2)

# ---------------------- 低通滤波器（高斯） ----------------------
low_pass_mask = np.exp(-(distance**2) / (2 * 30**2))
low_pass_mask = np.stack([low_pass_mask, low_pass_mask], axis=-1)
dft_low = dft_shift * low_pass_mask
img_low = idft_process(dft_low, new_h, new_w)

# ---------------------- 高通滤波器（高斯） ----------------------
high_pass_mask = 1 - low_pass_mask
dft_high = dft_shift * high_pass_mask
img_high = idft_process(dft_high, new_h, new_w)

# ---------------------- 带阻滤波器（去除指定频率） ----------------------
# 抑制距离中心50-80的频率
band_stop_mask = np.ones_like(dft_shift)
band_stop_mask[(distance >= 50) & (distance <= 80)] = 0
dft_band_stop = dft_shift * band_stop_mask
img_band_stop = idft_process(dft_band_stop, new_h, new_w)

# ---------------------- 带通滤波器（保留指定频率） ----------------------
band_pass_mask = np.zeros_like(dft_shift)
band_pass_mask[(distance >= 50) & (distance <= 80)] = 1
dft_band_pass = dft_shift * band_pass_mask
img_band_pass = idft_process(dft_band_pass, new_h, new_w)

# ---------------------- 可视化 ----------------------
plt.figure(figsize=(16, 12))

plt.subplot(2, 4, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

plt.subplot(2, 4, 2)
plt.imshow(img_low, cmap='gray')
plt.title('3.7 低通滤波器')
plt.axis('off')

plt.subplot(2, 4, 3)
plt.imshow(img_high, cmap='gray')
plt.title('3.7 高通滤波器')
plt.axis('off')

plt.subplot(2, 4, 4)
plt.imshow(img_band_stop, cmap='gray')
plt.title('3.7 带阻滤波器')
plt.axis('off')

plt.subplot(2, 4, 5)
plt.imshow(img_band_pass, cmap='gray')
plt.title('3.7 带通滤波器')
plt.axis('off')

# 掩码可视化
plt.subplot(2, 4, 6)
plt.imshow(low_pass_mask[:, :, 0], cmap='gray')
plt.title('低通掩码')
plt.axis('off')

plt.subplot(2, 4, 7)
plt.imshow(high_pass_mask[:, :, 0], cmap='gray')
plt.title('高通掩码')
plt.axis('off')

plt.subplot(2, 4, 8)
plt.imshow(band_stop_mask[:, :, 0], cmap='gray')
plt.title('带阻掩码')
plt.axis('off')

plt.tight_layout()
plt.show()

3.8 组合使用空间增强方法

应用场景

实际项目中，单一增强方法往往效果有限，需组合多种方法（如先去噪→再增强对比度→最后锐化）。

完整代码实现

复制代码

import numpy as np
import cv2
import matplotlib.pyplot as plt

# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 模拟低质量图像（噪声+低对比度+模糊）
img = cv2.imread('lena.jpg', cv2.IMREAD_GRAYSCALE)
# 1. 添加高斯噪声
img_noise = img + np.random.normal(0, 15, img.shape).astype(np.uint8)
# 2. 降低对比度
img_low_contrast = cv2.convertScaleAbs(img_noise, alpha=0.6, beta=30)
# 3. 模糊
img_blur = cv2.GaussianBlur(img_low_contrast, (3,3), 1)
# 最终低质量图像
img_bad = img_blur

# ---------------------- 组合增强流程 ----------------------
# 步骤1：中值滤波去噪声
img_step1 = cv2.medianBlur(img_bad, 3)

# 步骤2：CLAHE增强局部对比度
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8,8))
img_step2 = clahe.apply(img_step1)

# 步骤3：高提升滤波锐化
img_blur_step3 = cv2.GaussianBlur(img_step2, (5,5), 1)
mask = img_step2 - img_blur_step3
img_step3 = img_step2 + 1.5 * mask
img_step3 = np.clip(img_step3, 0, 255).astype(np.uint8)

# ---------------------- 可视化 ----------------------
plt.figure(figsize=(16, 8))

plt.subplot(2, 3, 1)
plt.imshow(img, cmap='gray')
plt.title('原始高质量图像')
plt.axis('off')

plt.subplot(2, 3, 2)
plt.imshow(img_bad, cmap='gray')
plt.title('低质量图像（噪声+低对比度+模糊）')
plt.axis('off')

plt.subplot(2, 3, 3)
plt.imshow(img_step1, cmap='gray')
plt.title('步骤1：中值滤波去噪声')
plt.axis('off')

plt.subplot(2, 3, 4)
plt.imshow(img_step2, cmap='gray')
plt.title('步骤2：CLAHE增强对比度')
plt.axis('off')

plt.subplot(2, 3, 5)
plt.imshow(img_step3, cmap='gray')
plt.title('步骤3：高提升滤波锐化')
plt.axis('off')

# 对比直方图
plt.subplot(2, 3, 6)
plt.hist(img_bad.ravel(), bins=256, range=[0,255], alpha=0.5, label='低质量')
plt.hist(img_step3.ravel(), bins=256, range=[0,255], alpha=0.5, label='增强后')
plt.title('直方图对比')
plt.xlabel('灰度值')
plt.ylabel('像素数')
plt.legend()

plt.tight_layout()
plt.show()

效果说明

组合增强的核心逻辑是先去噪→再增强对比度→最后锐化，避免锐化放大噪声、对比度增强放大噪声等问题，是工程中最常用的图像增强流程。

总结

本章系统讲解了灰度变换与空间滤波的核心知识点，从基础原理到代码实现，结合可视化对比让每个知识点都直观易懂。核心要点：

灰度变换是点操作，适合全局对比度 / 亮度调整；
空间滤波是邻域操作，分为平滑（低通）和锐化（高通）；
实际应用中需组合多种方法，遵循 "去噪→增强→锐化" 的流程；
频域滤波适合复杂滤波器（如带阻 / 带通），空域滤波更易实现和部署。

所有代码均可直接运行，建议读者替换不同的测试图像（如低对比度、含噪声、模糊图像），调整参数（如核大小、γ 值、σ 值），观察效果变化，加深对知识点的理解。