一、排序 + 二分查找:基于有序结构的高效查找
1.1. 基本流程
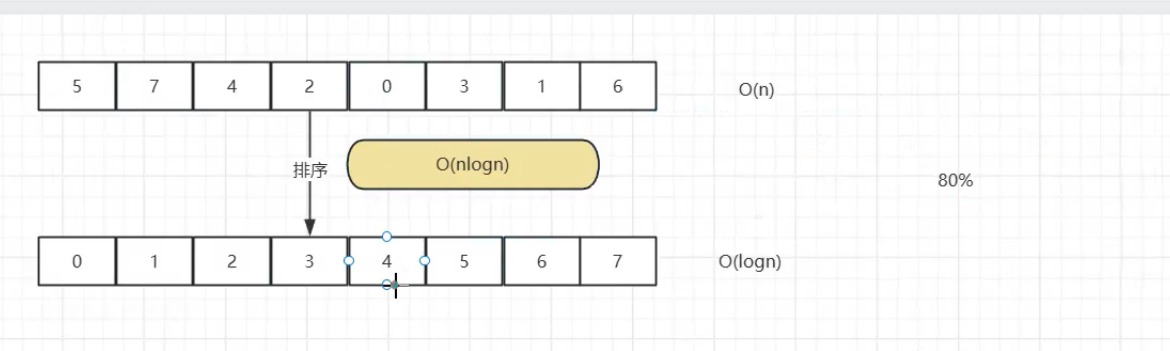
对于无序数据集,先通过排序将其转化为有序结构,再利用二分查找实现高效查询:
排序阶段:采用时间复杂度为 O(nlogn) 的算法(如快速排序、归并排序),将数据集调整为有序序列。
查找阶段:二分查找通过 "分治" 思想,每次排除一半数据,时间复杂度为 O(logn)。
1.2. 示例
以数据集 [5,7,4,2,0,3,1,6] 为例:
- 排序后得到有序序列
[0,1,2,3,4,5,6,7]; - 查找元素
4:- 初始区间
[0,7],中间元素为3(小于 4),缩小到右区间[4,7]; - 中间元素为
5(大于 4),缩小到左区间[4,4],找到目标元素。
- 初始区间
1.3. 局限性
排序操作的开销较高,若数据集频繁增删,需重复排序,整体效率下降。
二、哈希表:O (1) 级别的存储与查找
2.1. 核心原理
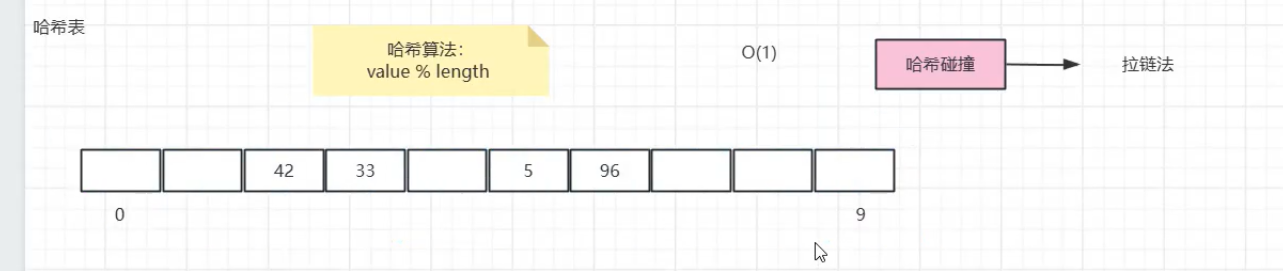
哈希表通过哈希函数将数据映射到数组的指定索引(即 "桶"),实现直接访问:
哈希函数:常见实现为 value % 数组长度(需保证数组长度为质数以减少冲突);
理想情况下,插入、查找、删除操作的时间复杂度均为 O(1)。
2.2. 哈希冲突及解决
当不同数据映射到同一索引时,会发生 "哈希冲突",常用拉链法解决:将冲突元素以链表 / 树的形式存储在同一桶下。
2.3. 示例
以数组长度为 10 的哈希表存储数据 42,33,5,96:
42%10=2 → 存入索引 2;
33%10=3 → 存入索引 3;
若存入 9(9%10=9),后续存入 19 时发生冲突,将 19 链入索引 9 的链表中。
三、树结构:动态数据的高效分层存储
当数据量较大且需频繁增删时,树结构通过分层组织数据,平衡存储与查询效率。
3.1. 二叉排序树(BST)
3.1.1.定义
二叉排序树满足:左子树所有节点值 < 父节点值 < 右子树所有节点值。
3.1.2.操作复杂度
理想情况下(树结构平衡),插入、查找、删除的时间复杂度为 O(logn);
若数据有序,BST 会退化为单链表,操作复杂度劣化为 O(n)。
3.1.3.示例
存储数据集 [5,3,1,4,8,9,7] 的 BST 结构:
java
5
/ \
3 8
/ \ / \
1 4 7 9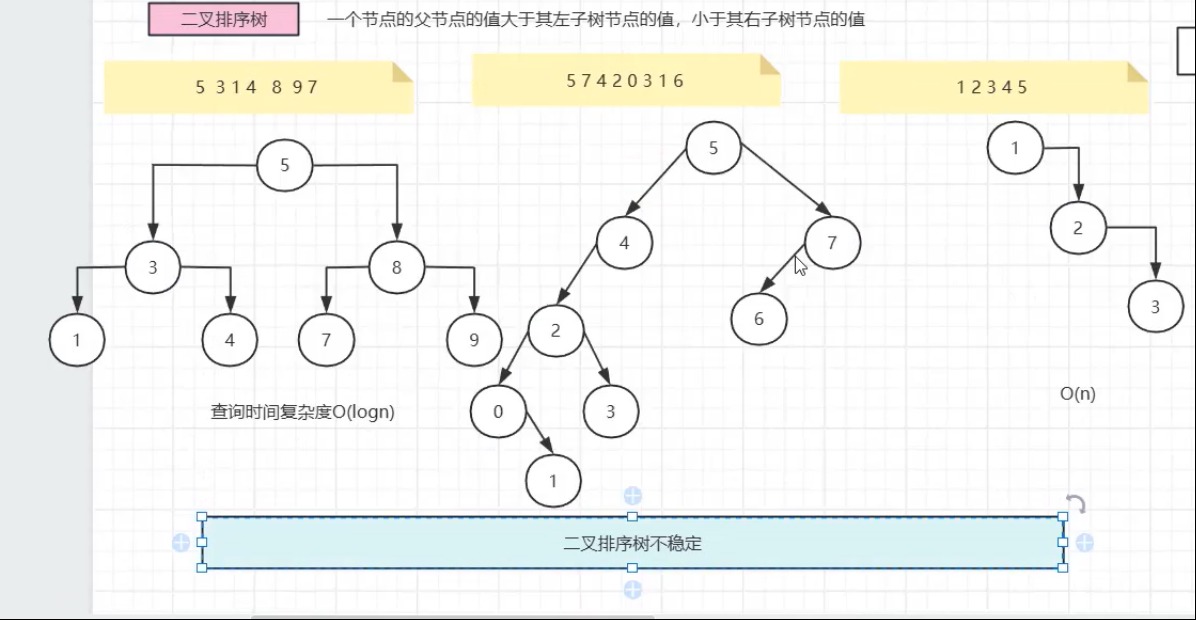
3.2. 平衡二叉树(AVL 树)
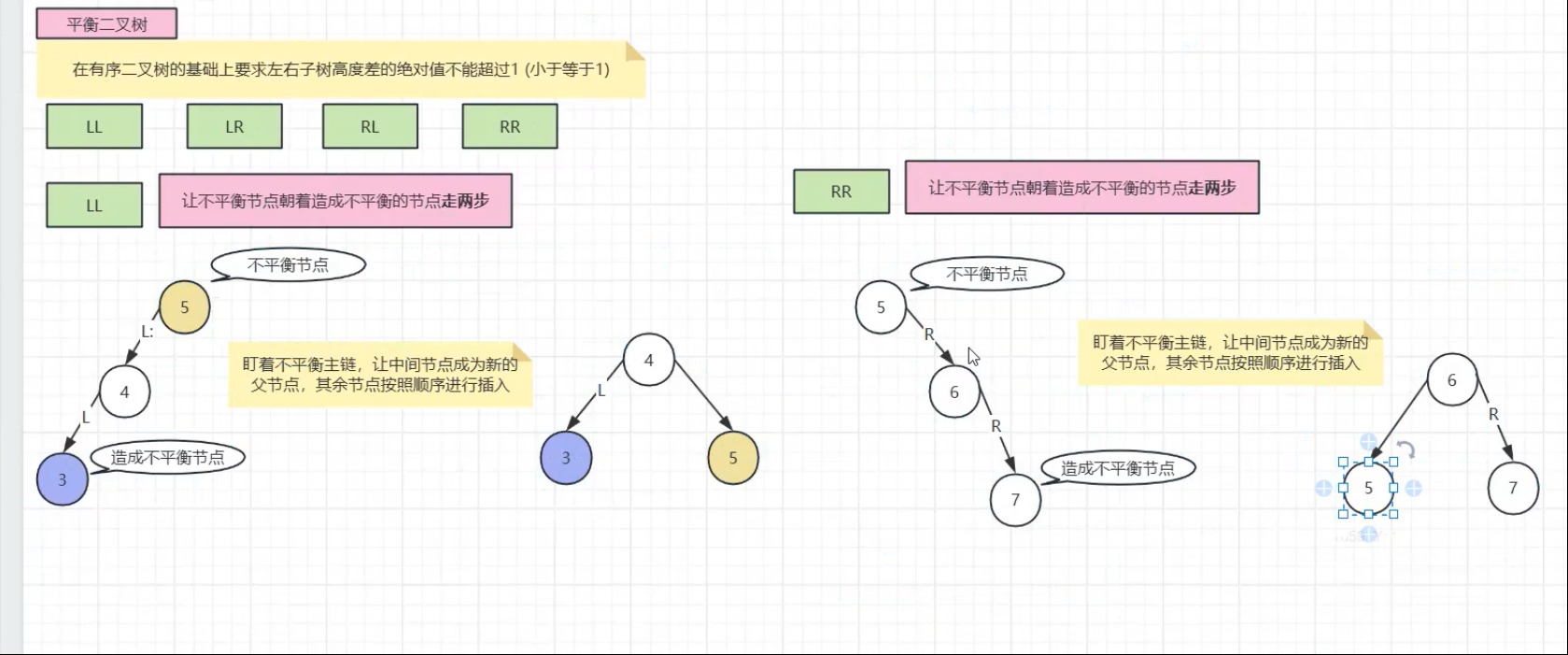
为解决 BST 的退化问题,AVL 树通过平衡因子(左右子树高度差的绝对值)限制树的形态:
平衡因子需 ≤ 1;
当插入 / 删除导致失衡时,通过旋转操作调整结构:
LL/RR 旋转:单方向失衡时,将中间节点提升为父节点;
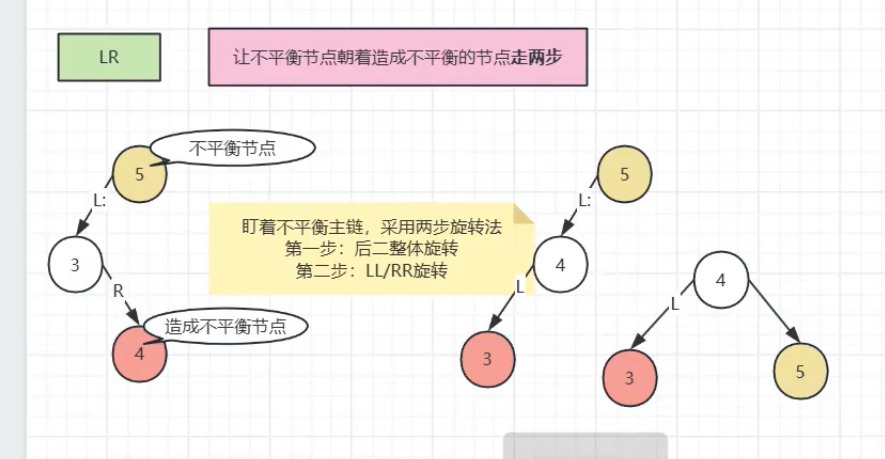
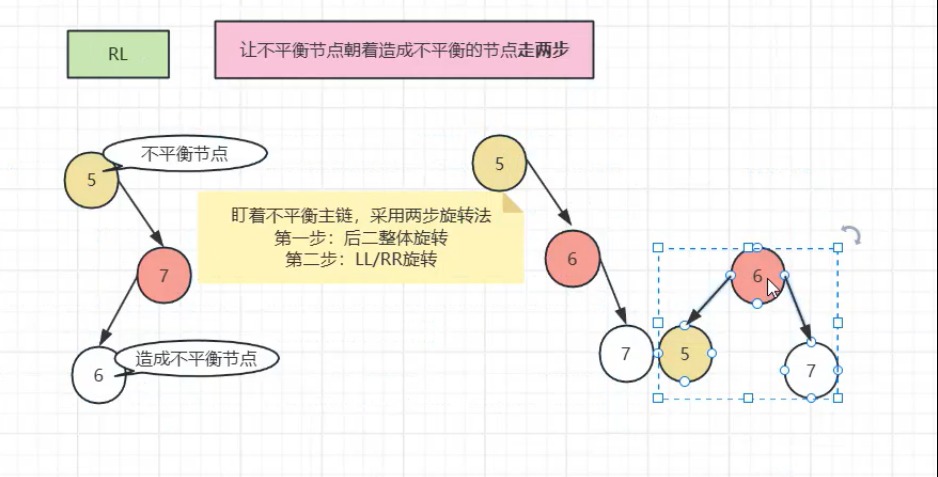
LR/RL 旋转:双向失衡时,先调整子树方向,再执行单旋转。
AVL 树的操作复杂度稳定为 O(logn),但旋转操作开销较高。
3.3. 红黑树
红黑树通过颜色规则维持近似平衡,降低调整频率:
- 红黑树的节点颜色不是红色就是黑色的;
- 根节点与叶子节点都为黑色;
- 如果一个节点是红色的,那么他的子节点必为黑色;
- 从根节点出发到任意一个叶子节点,所走过的路径上黑色节点的数目是相同的
红黑树的最长路径不超过最短路径的 2 倍,操作复杂度为 O(logn),是工程中常用的高效结构(如 Java 的 TreeMap、HashMap)。