一、概述
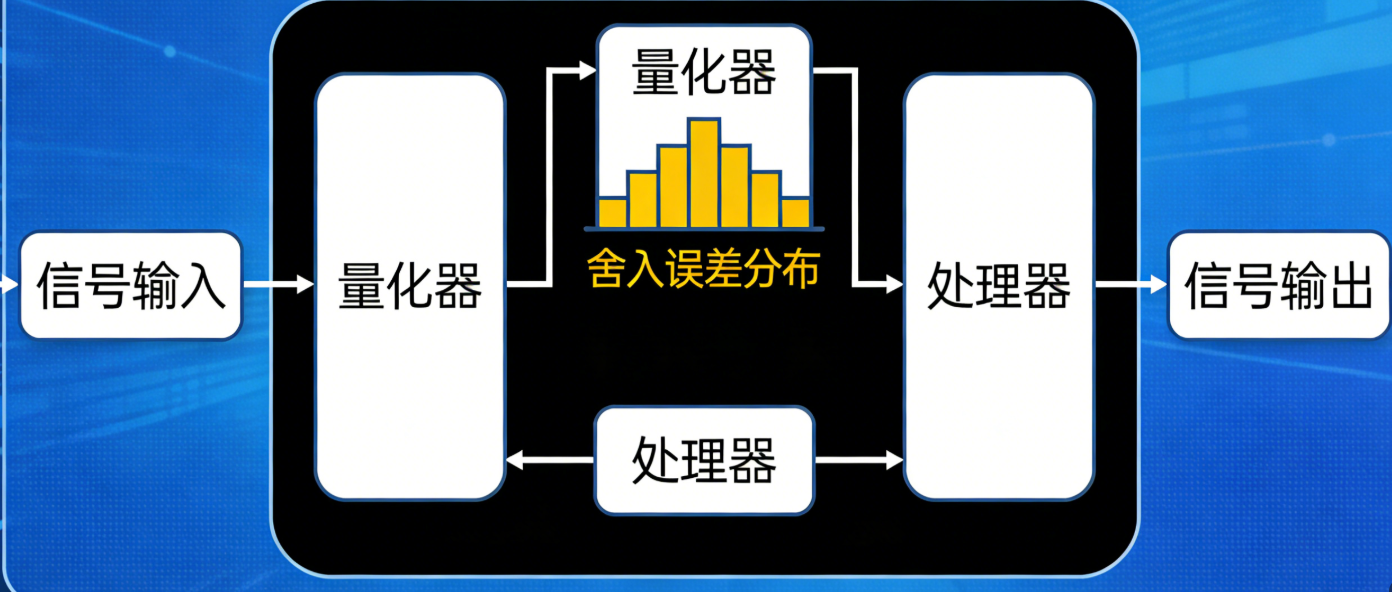
有限字长效应是数字信号处理中不可忽视的重要问题,它源于数字系统中有限的二进制位数表示。在实际的数字信号处理器(DSP)和FPGA实现中,我们必须面对量化误差、舍入误差和溢出等问题。本章将系统地讲解这些问题及其影响。
二、二进制数的表示及其量化影响
2.1 二进制算术运算与负数表示
Matlab
%% 二进制表示与负数表示演示(终极完美修正版)
% 解决问题:1. bitcmp函数参数错误 2. 赋值字符数不匹配 3. 手动补码计算不通用
% 优化点:自动化计算反码/补码,统一位数管理,补码减法全程无手动干预
clear all; close all; clc;
% 核心参数:4位有符号二进制(符号位1位+数值位3位,范围-8~7)
bit_width = 4;
sign_bit = 1; % 最高位为符号位
num_bits = bit_width - sign_bit; % 数值位位数:3
test_values = [7, 5, 0, -5, -7]; % 测试数值
fprintf('========== %d位有符号二进制:原码、反码、补码表示 ==========\n', bit_width);
for i = 1:length(test_values)
value = test_values(i);
abs_val = abs(value);
% 1. 原码:正数=0+数值位,负数=1+数值位(严格按位数拆分,无错位)
if value >= 0
original = [repmat('0',1,sign_bit), dec2bin(abs_val, num_bits)];
else
original = [repmat('1',1,sign_bit), dec2bin(abs_val, num_bits)];
end
% 2. 反码:正数=原码;负数=符号位不变,数值位按位取反(自动化,无手动赋值)
if value >= 0
ones_complement = original;
else
sign_part = original(1:sign_bit); % 提取符号位(保持不变)
num_part = original(sign_bit+1:end);% 提取数值位(需要取反)
% 数值位按位取反(0↔1,自动化实现,适配任意数值位位数)
num_part(num_part=='0') = '2';
num_part(num_part=='1') = '0';
num_part(num_part=='2') = '1';
ones_complement = [sign_part, num_part]; % 拼接符号位+取反后数值位
end
% 3. 补码:正数=原码;负数=反码+1(二进制加法,逢2进1,自动化)
if value >= 0
twos_complement = original;
else
% 反码转十进制加1,再转回固定位数二进制(无位数丢失)
ones_dec = bin2dec(ones_complement);
twos_dec = ones_dec + 1;
twos_complement = dec2bin(twos_dec, bit_width);
end
% 格式化打印,对齐输出
fprintf('十进制: %3d, 原码: %4s, 反码: %4s, 补码: %4s\n', ...
value, original, ones_complement, twos_complement);
end
% 二进制加减法演示(补码核心:减法转加法 A-B = A + (-B),全程自动化)
fprintf('\n========== %d位有符号二进制加减法演示(补码运算核心) ==========\n', bit_width);
A = 5; % 0101
B = 3; % 0011
fprintf('基础数值:%d(%s), %d(%s)\n', A, dec2bin(A,bit_width), B, dec2bin(B,bit_width));
% 1. 加法运算:直接二进制相加,保留固定位数
sum_dec = A + B;
sum_bin = dec2bin(sum_dec, bit_width);
fprintf('%d + %d = %d (二进制: %4s)\n', A, B, sum_dec, sum_bin);
% 2. 减法运算:A-B = A + (-B),全程自动化计算补码,无手动赋值(核心修正)
% 步骤1:求A的补码(正数补码=原码)
A_twos = [repmat('0',1,sign_bit), dec2bin(A, num_bits)];
% 步骤2:自动化求-B的补码(原码→反码→补码,无手动干预,解决赋值不匹配)
B_neg = -B;
abs_B_neg = abs(B_neg);
% -B的原码
B_neg_original = [repmat('1',1,sign_bit), dec2bin(abs_B_neg, num_bits)];
% -B的反码(符号位不变,数值位自动化取反)
B_neg_sign = B_neg_original(1:sign_bit);
B_neg_num = B_neg_original(sign_bit+1:end);
B_neg_num(B_neg_num=='0') = '2';
B_neg_num(B_neg_num=='1') = '0';
B_neg_num(B_neg_num=='2') = '1';
B_neg_ones = [B_neg_sign, B_neg_num];
% -B的补码(反码+1)
B_neg_twos = dec2bin(bin2dec(B_neg_ones)+1, bit_width);
% 步骤3:补码相加(含进位,完整展示运算过程)
A_twos_dec = bin2dec(A_twos);
B_neg_twos_dec = bin2dec(B_neg_twos);
twos_sum_dec = A_twos_dec + B_neg_twos_dec;
twos_sum_bin = dec2bin(twos_sum_dec, bit_width+1); % 多1位展示进位
% 步骤4:结果截取固定位数(4位有符号,舍弃高位进位)
result_bin = twos_sum_bin(end-bit_width+1:end);
result_dec = A - B;
% 完整打印补码减法运算过程,清晰展示原理
fprintf('\n【补码核心原理】减法转加法:%d - %d = %d + (%d)\n', A, B, A, B_neg);
fprintf('【补码运算过程】%s(%d) + %s(%d的补码) = %s(含进位)→ 截取%d位:%s\n', ...
A_twos, A, B_neg_twos, B_neg, twos_sum_bin, bit_width, result_bin);
fprintf('【最终结果】%d - %d = %d(二进制:%4s)\n', A, B, result_dec, result_bin);
% 关键知识点总结
fprintf('\n========== 核心知识点总结 ==========\n');
fprintf('1. %d位有符号二进制范围:补码[-%d, %d],原码/反码[-%d, %d]\n', ...
bit_width, 2^num_bits, 2^num_bits-1, 2^num_bits-1, 2^num_bits-1);
fprintf('2. 补码唯一表示0(%s),无原码/反码的+0/-0之分\n', repmat('0',1,bit_width));
fprintf('3. 硬件优势:补码将减法转为加法,统一运算电路,降低硬件复杂度\n');
fprintf('4. 取反规则:负数补码 = 符号位不变 + 数值位取反 + 1(二进制)\n');2.2 量化方式对比:舍入与截尾
Matlab
%% 量化方式对比:舍入与截尾
clear all; close all; clc;
% 生成测试信号
t = 0:0.01:2*pi;
x = 2.5*sin(t) + 0.5*cos(3*t);
% 量化函数
quantize_round = @(x, bits) round(x * 2^(bits-1)) / 2^(bits-1);
quantize_truncate = @(x, bits) floor(x * 2^(bits-1)) / 2^(bits-1);
% 不同比特数的量化
bits_list = [3, 5, 8];
colors = ['r', 'g', 'b'];
figure('Position', [100, 100, 1200, 800]);
% 绘制原始信号
subplot(3, 1, 1);
plot(t, x, 'b-', 'LineWidth', 2);
hold on;
for i = 1:length(bits_list)
bits = bits_list(i);
x_round = quantize_round(x, bits);
plot(t, x_round, [colors(i), '--'], 'LineWidth', 1.5, ...
'DisplayName', sprintf('%d-bit 舍入', bits));
end
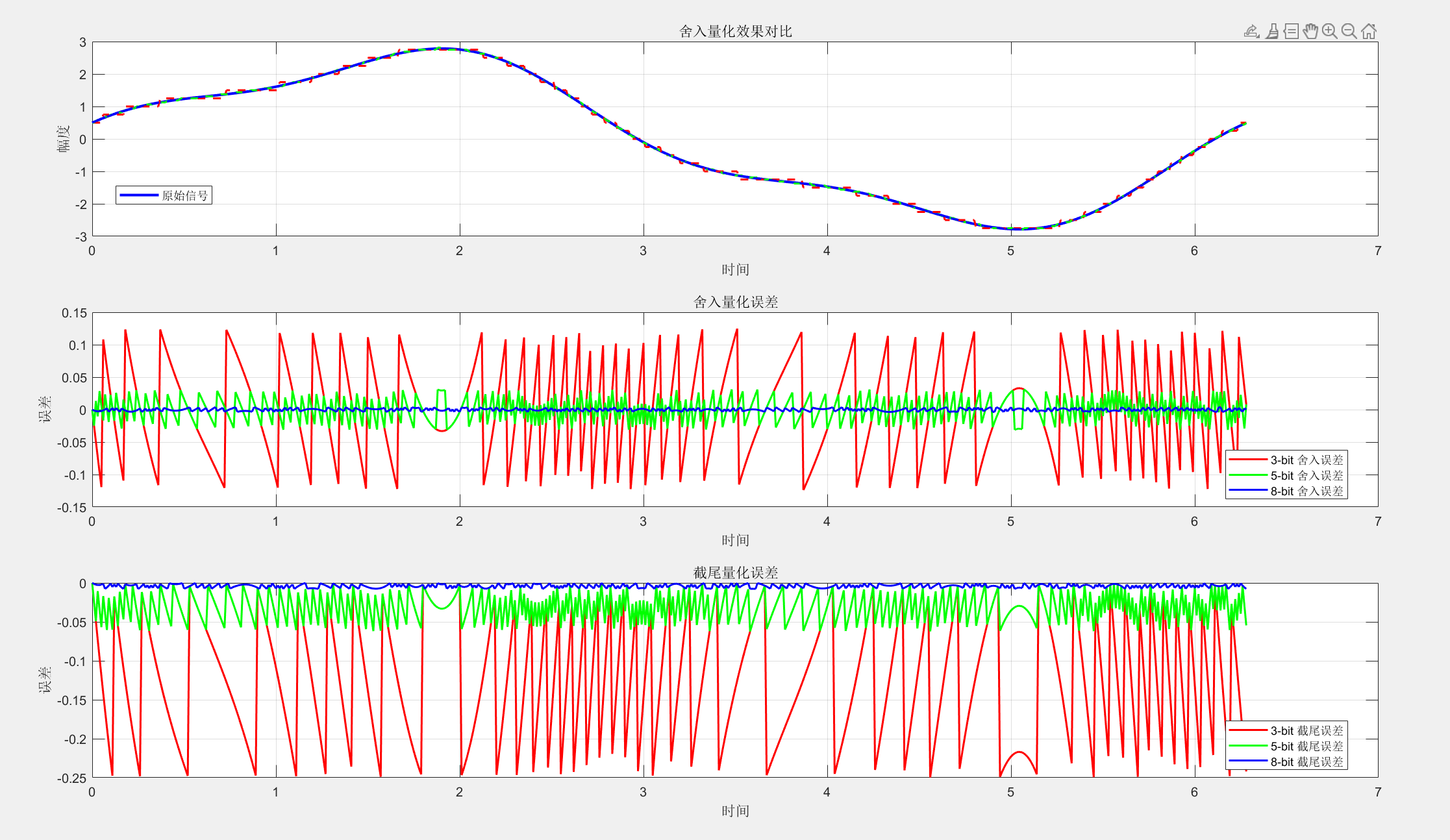
title('舍入量化效果对比');
xlabel('时间'); ylabel('幅度');
legend('原始信号', 'Location', 'best');
grid on;
% 绘制舍入误差
subplot(3, 1, 2);
for i = 1:length(bits_list)
bits = bits_list(i);
x_round = quantize_round(x, bits);
error_round = x_round - x;
plot(t, error_round, [colors(i), '-'], 'LineWidth', 1.5, ...
'DisplayName', sprintf('%d-bit 舍入误差', bits));
hold on;
end
title('舍入量化误差');
xlabel('时间'); ylabel('误差');
legend('Location', 'best');
grid on;
% 绘制截尾误差
subplot(3, 1, 3);
for i = 1:length(bits_list)
bits = bits_list(i);
x_truncate = quantize_truncate(x, bits);
error_truncate = x_truncate - x;
plot(t, error_truncate, [colors(i), '-'], 'LineWidth', 1.5, ...
'DisplayName', sprintf('%d-bit 截尾误差', bits));
hold on;
end
title('截尾量化误差');
xlabel('时间'); ylabel('误差');
legend('Location', 'best');
grid on;
% 统计量化误差
fprintf('\n========== 量化误差统计分析 ==========\n');
for bits = [4, 8, 12]
% 舍入量化
x_round = quantize_round(x, bits);
error_round = x_round - x;
% 截尾量化
x_truncate = quantize_truncate(x, bits);
error_truncate = x_truncate - x;
fprintf('\n%d-bit 量化:\n', bits);
fprintf('舍入 - 均方误差: %.6f, 最大误差: %.6f\n', ...
mean(error_round.^2), max(abs(error_round)));
fprintf('截尾 - 均方误差: %.6f, 最大误差: %.6f\n', ...
mean(error_truncate.^2), max(abs(error_truncate)));
end三、A/D变换的量化效应
3.1 A/D变换非线性模型与量化噪声分析
Matlab
%% A/D变换量化效应分析
clear all; close all; clc;
% 参数设置
Fs = 1000; % 采样频率
T = 1/Fs; % 采样间隔
t = 0:T:1-T; % 时间向量
f1 = 50; % 信号频率
f2 = 120; % 信号频率
% 生成多频信号
x = 0.7*sin(2*pi*f1*t) + sin(2*pi*f2*t);
% 量化函数
adc_quantize = @(x, bits, vref) round(x/vref * (2^(bits-1)-1)) / (2^(bits-1)-1) * vref;
% 不同比特数量化
bits_list = [4, 8, 12, 16];
vref = 2.0; % 参考电压
figure('Position', [100, 100, 1400, 900]);
% 时域对比
for i = 1:length(bits_list)
subplot(2, 2, i);
bits = bits_list(i);
% 量化信号
x_quantized = adc_quantize(x, bits, vref);
% 绘制时域信号
plot(t(1:100), x(1:100), 'b-', 'LineWidth', 2);
hold on;
plot(t(1:100), x_quantized(1:100), 'r--', 'LineWidth', 1.5);
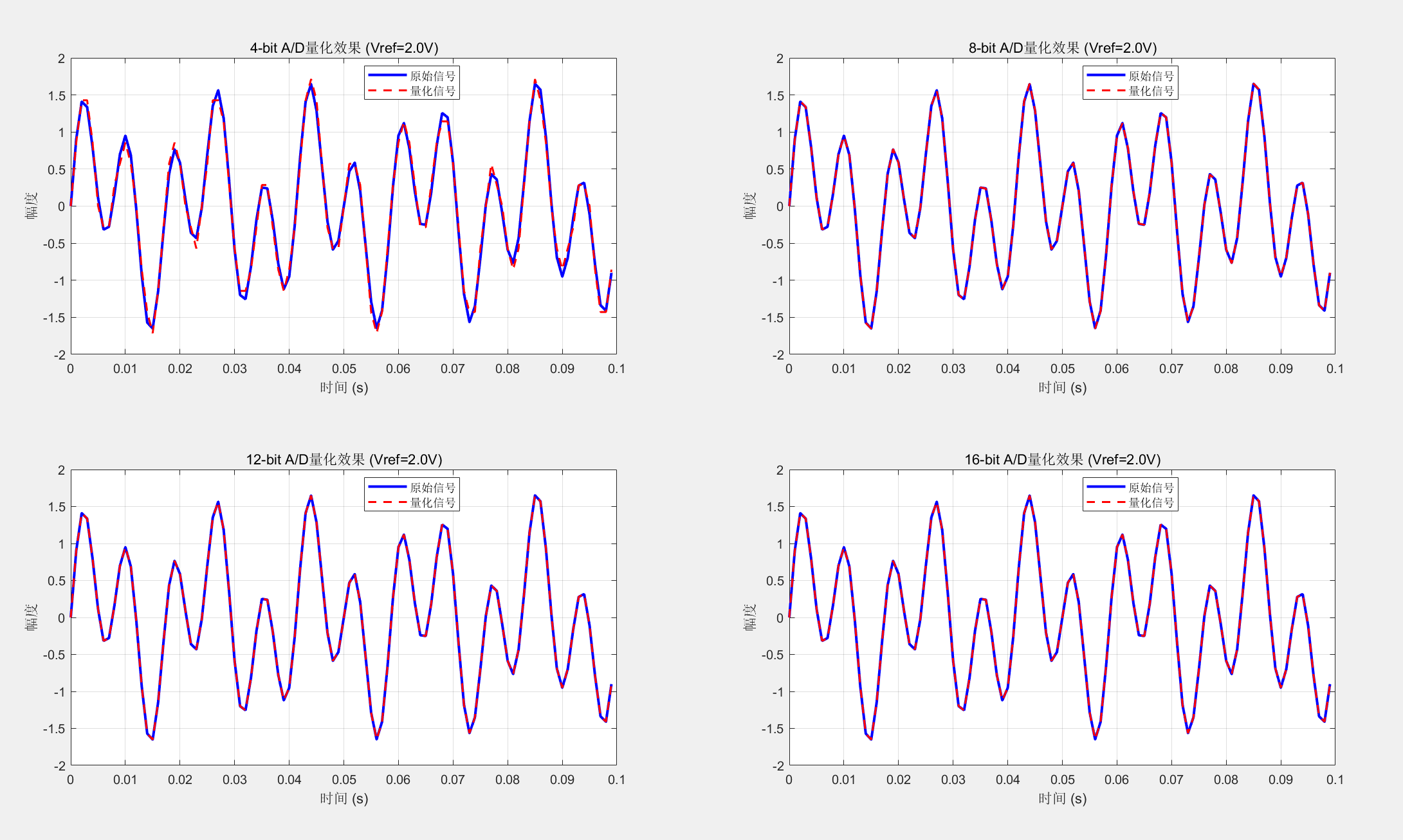
title(sprintf('%d-bit A/D量化效果 (Vref=%.1fV)', bits, vref));
xlabel('时间 (s)'); ylabel('幅度');
legend('原始信号', '量化信号', 'Location', 'best');
grid on;
end
% 频域分析
figure('Position', [100, 100, 1400, 900]);
for i = 1:length(bits_list)
subplot(2, 2, i);
bits = bits_list(i);
% 量化信号
x_quantized = adc_quantize(x, bits, vref);
% 计算FFT
N = length(x);
f = Fs*(0:(N/2))/N;
X = fft(x);
X_quantized = fft(x_quantized);
P2 = abs(X/N);
P1 = P2(1:N/2+1);
P1(2:end-1) = 2*P1(2:end-1);
P2_q = abs(X_quantized/N);
P1_q = P2_q(1:N/2+1);
P1_q(2:end-1) = 2*P1_q(2:end-1);
% 绘制频谱
plot(f, 20*log10(P1), 'b-', 'LineWidth', 2);
hold on;
plot(f, 20*log10(P1_q), 'r--', 'LineWidth', 1.5);
title(sprintf('%d-bit A/D量化频谱对比', bits));
xlabel('频率 (Hz)'); ylabel('幅度 (dB)');
xlim([0, Fs/2]);
legend('原始信号', '量化信号', 'Location', 'best');
grid on;
end
% 量化噪声统计分析
fprintf('\n========== A/D量化噪声统计分析 ==========\n');
for bits = [4, 8, 12, 16]
% 量化信号
x_quantized = adc_quantize(x, bits, vref);
% 量化误差
quantization_error = x_quantized - x;
% 统计特性
error_mean = mean(quantization_error);
error_var = var(quantization_error);
error_std = std(quantization_error);
snr = 10*log10(var(x) / error_var);
fprintf('\n%d-bit A/D转换:\n', bits);
fprintf(' 量化误差均值: %.6f\n', error_mean);
fprintf(' 量化误差方差: %.6f\n', error_var);
fprintf(' 量化误差标准差: %.6f\n', error_std);
fprintf(' 信噪比(SNR): %.2f dB\n', snr);
% 理论SNR:SNR = 6.02*N + 1.76 dB
theoretical_snr = 6.02*bits + 1.76;
fprintf(' 理论SNR: %.2f dB\n', theoretical_snr);
end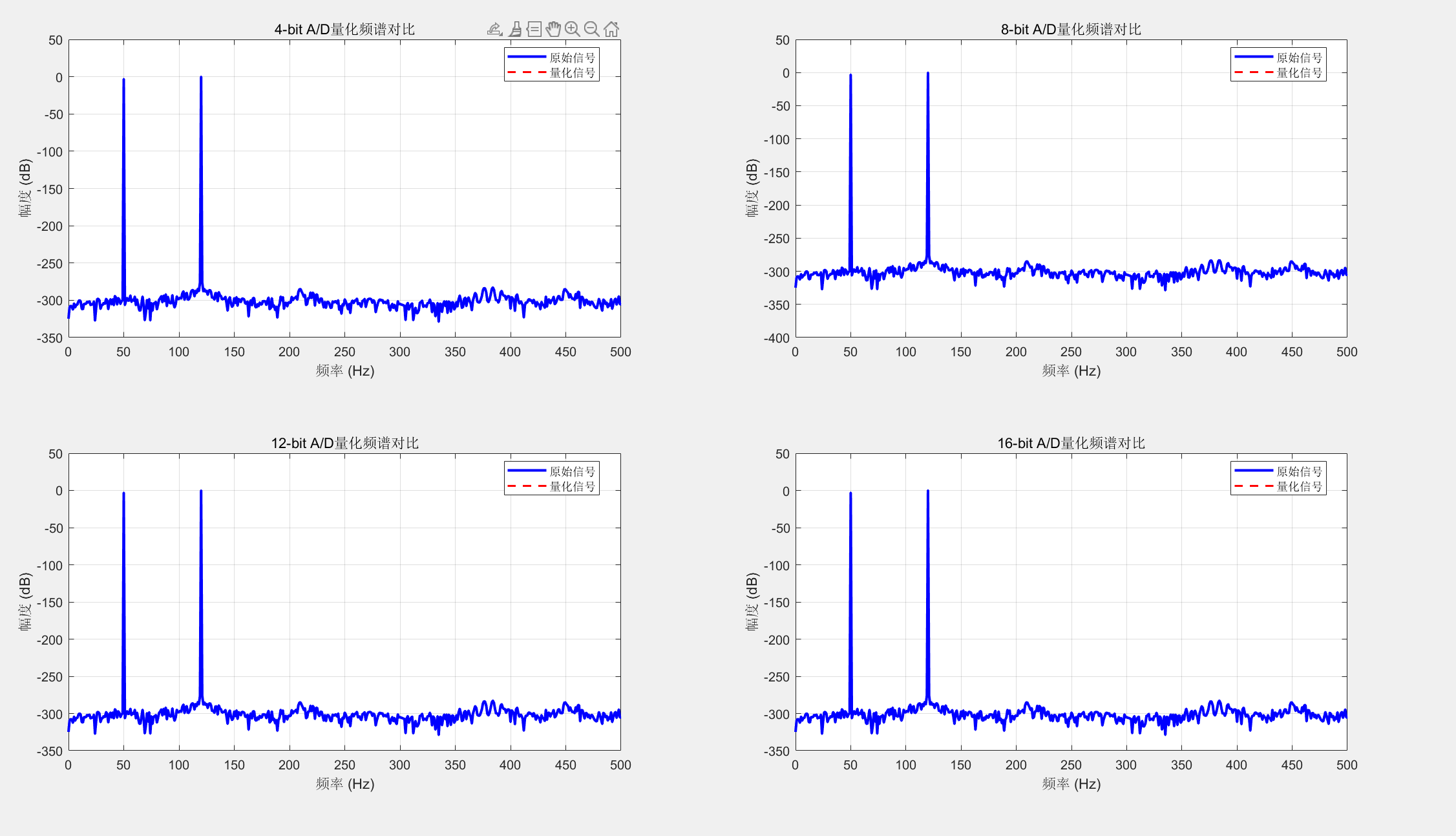
四、数字滤波器的系数量化效应
4.1 极点位置灵敏度分析
Matlab
%% 数字滤波器系数量化效应分析
clear all; close all; clc;
% 设计一个IIR滤波器
Fs = 1000; % 采样频率
fpass = 100; % 通带频率
fstop = 150; % 阻带频率
Rp = 1; % 通带波纹
Rs = 40; % 阻带衰减
% 设计椭圆滤波器
[n, Wn] = ellipord(fpass/(Fs/2), fstop/(Fs/2), Rp, Rs);
[b, a] = ellip(n, Rp, Rs, Wn);
% 原始滤波器的零极点
[z_orig, p_orig, k_orig] = tf2zp(b, a);
% 量化函数
quantize_coeff = @(coeff, bits) round(coeff * 2^(bits-1)) / 2^(bits-1);
% 不同比特数量化
bits_list = [8, 12, 16];
figure('Position', [100, 100, 1200, 1000]);
% 绘制零极点图
subplot(2, 2, 1);
zplane(z_orig, p_orig);
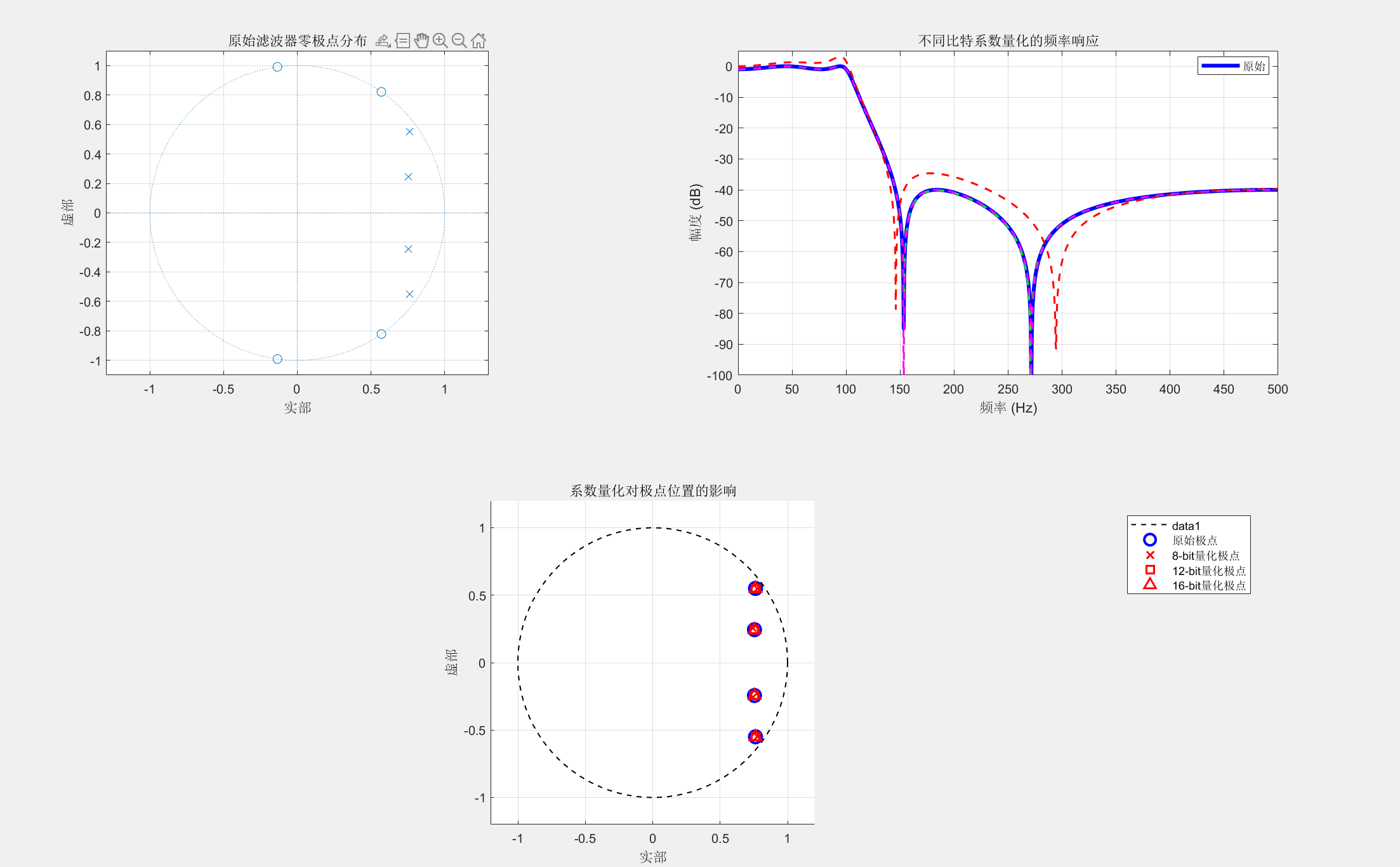
title('原始滤波器零极点分布');
grid on;
% 频率响应对比
subplot(2, 2, 2);
[h_orig, w_orig] = freqz(b, a, 1024, Fs);
plot(w_orig, 20*log10(abs(h_orig)), 'b-', 'LineWidth', 3);
hold on;
colors = ['r', 'g', 'm'];
for i = 1:length(bits_list)
bits = bits_list(i);
% 量化系数
b_quant = quantize_coeff(b, bits);
a_quant = quantize_coeff(a, bits);
% 计算频率响应
[h_quant, w_quant] = freqz(b_quant, a_quant, 1024, Fs);
plot(w_quant, 20*log10(abs(h_quant)), [colors(i), '--'], ...
'LineWidth', 1.5, 'DisplayName', sprintf('%d-bit', bits));
end
title('不同比特系数量化的频率响应');
xlabel('频率 (Hz)'); ylabel('幅度 (dB)');
xlim([0, Fs/2]); ylim([-100, 5]);
legend('原始', 'Location', 'best');
grid on;
% 量化对极点位置的影响
subplot(2, 2, [3, 4]);
hold on;
% 绘制单位圆
theta = linspace(0, 2*pi, 100);
plot(cos(theta), sin(theta), 'k--', 'LineWidth', 1);
axis equal;
xlim([-1.2, 1.2]); ylim([-1.2, 1.2]);
grid on;
% 绘制原始极点
plot(real(p_orig), imag(p_orig), 'bo', 'MarkerSize', 10, ...
'LineWidth', 2, 'DisplayName', '原始极点');
% 绘制量化后的极点
markers = ['x', 's', '^'];
for i = 1:length(bits_list)
bits = bits_list(i);
% 量化系数
b_quant = quantize_coeff(b, bits);
a_quant = quantize_coeff(a, bits);
% 获取量化后的极点
[~, p_quant, ~] = tf2zp(b_quant, a_quant);
plot(real(p_quant), imag(p_quant), [markers(i), 'r'], ...
'MarkerSize', 8, 'LineWidth', 1.5, ...
'DisplayName', sprintf('%d-bit量化极点', bits));
end
title('系数量化对极点位置的影响');
xlabel('实部'); ylabel('虚部');
legend('Location', 'best');
% 稳定性分析
fprintf('\n========== 滤波器稳定性分析 ==========\n');
for bits = [8, 12, 16]
% 量化系数
b_quant = quantize_coeff(b, bits);
a_quant = quantize_coeff(a, bits);
% 获取极点
[~, p_quant, ~] = tf2zp(b_quant, a_quant);
% 检查稳定性(所有极点应在单位圆内)
max_pole_magnitude = max(abs(p_quant));
is_stable = max_pole_magnitude < 1;
fprintf('\n%d-bit 系数量化:\n', bits);
fprintf(' 最大极点幅值: %.6f\n', max_pole_magnitude);
fprintf(' 滤波器稳定: %s\n', string(is_stable));
if ~is_stable
fprintf(' 警告: 量化导致滤波器不稳定!\n');
end
end4.2 二阶子系统极点位置影响
Matlab
%% 二阶子系统极点位置对系数量化的灵敏度
clear all; close all; clc;
% 设计二阶IIR滤波器(直接II型结构)
r = 0.95; % 极点半径
theta = pi/4; % 极点角度
% 极点位置
p1 = r * exp(1j*theta);
p2 = r * exp(-1j*theta);
% 构造滤波器系数
a = [1, -2*r*cos(theta), r^2]; % 分母系数
b = [1, 0, 0]; % 分子系数
% 量化函数
quantize_coeff = @(coeff, bits) round(coeff * 2^(bits-1)) / 2^(bits-1);
% 测试不同比特数
bits_list = [6, 8, 10, 12];
n_trials = 1000; % 蒙特卡洛模拟次数
figure('Position', [100, 100, 1400, 600]);
% 绘制极点位置分布
for idx = 1:length(bits_list)
bits = bits_list(idx);
subplot(2, length(bits_list)/2, idx);
hold on;
% 绘制单位圆
theta_circle = linspace(0, 2*pi, 100);
plot(cos(theta_circle), sin(theta_circle), 'k--', 'LineWidth', 1);
% 原始极点位置
plot(real(p1), imag(p1), 'bo', 'MarkerSize', 10, ...
'LineWidth', 2, 'DisplayName', '原始极点');
plot(real(p2), imag(p2), 'bo', 'MarkerSize', 10, 'LineWidth', 2);
% 蒙特卡洛模拟:随机量化误差
pole_positions = [];
for trial = 1:n_trials
% 添加随机量化误差
a_quant = a + (rand(1,3)-0.5) * 2^(-bits);
a_quant = quantize_coeff(a_quant, bits);
% 计算极点
p = roots(a_quant);
pole_positions = [pole_positions; p.'];
end
% 绘制量化后的极点分布
plot(real(pole_positions), imag(pole_positions), 'r.', ...
'MarkerSize', 6, 'DisplayName', '量化极点');
% 计算极点分布范围
pole_magnitudes = abs(pole_positions);
max_magnitude = max(pole_magnitudes);
min_magnitude = min(pole_magnitudes);
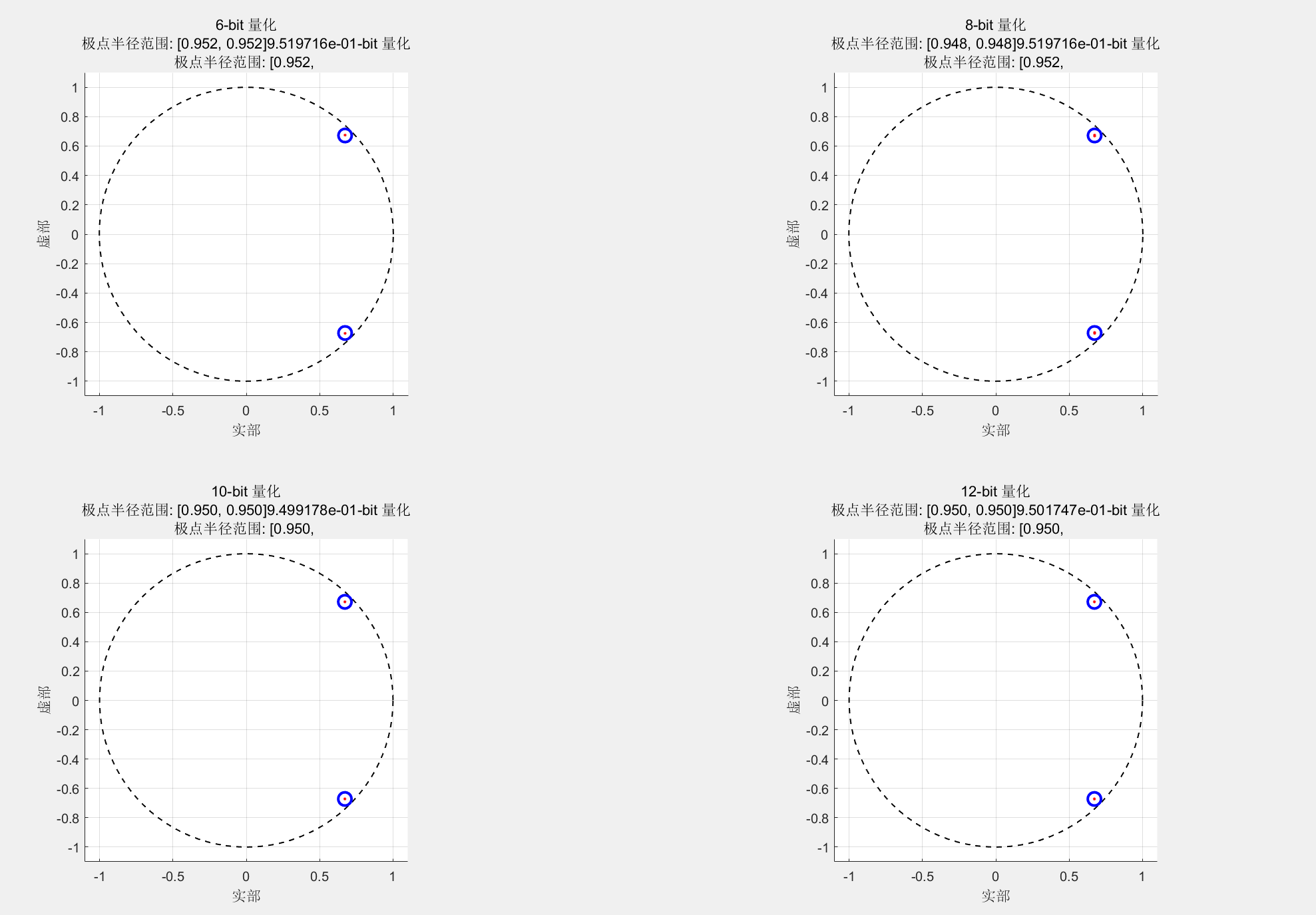
title(sprintf('%d-bit 量化\n极点半径范围: [%.3f, %.3f]', ...
bits, min_magnitude, max_magnitude));
xlabel('实部'); ylabel('虚部');
axis equal; grid on;
xlim([-1.1, 1.1]); ylim([-1.1, 1.1]);
% 添加稳定性边界(单位圆)
if any(pole_magnitudes >= 1)
text(-0.9, 0.8, '不稳定!', 'Color', 'r', 'FontSize', 12, ...
'FontWeight', 'bold');
end
end
% 灵敏度分析
fprintf('\n========== 二阶系统极点灵敏度分析 ==========\n');
fprintf('原始极点: r=%.3f, θ=%.3fπ\n', r, theta/pi);
fprintf('原始分母系数: a0=%.6f, a1=%.6f, a2=%.6f\n', a(1), a(2), a(3));
% 计算极点对系数的偏导数
syms z a1 a2;
eq = z^2 + a1*z + a2 == 0;
z_solutions = solve(eq, z);
% 在原始系数处求导
a1_val = -2*r*cos(theta);
a2_val = r^2;
% 计算灵敏度
dz_da1 = subs(diff(z_solutions(1), a1), {a1, a2}, {a1_val, a2_val});
dz_da2 = subs(diff(z_solutions(1), a2), {a1, a2}, {a1_val, a2_val});
fprintf('\n极点灵敏度分析:\n');
fprintf('∂p/∂a1 = %.6f + %.6fj\n', real(double(dz_da1)), imag(double(dz_da1)));
fprintf('∂p/∂a2 = %.6f + %.6fj\n', real(double(dz_da2)), imag(double(dz_da2)));
% 估计量化引起的极点变化
for bits = [8, 12, 16]
delta = 2^(-bits); % 量化步长
% 估计极点变化范围
delta_p_a1 = abs(double(dz_da1)) * delta;
delta_p_a2 = abs(double(dz_da2)) * delta;
total_delta = delta_p_a1 + delta_p_a2;
fprintf('\n%d-bit 量化 (步长=%.6f):\n', bits, delta);
fprintf(' 估计极点变化范围: ±%.6f\n', total_delta);
fprintf(' 相对变化: %.2f%%\n', 100*total_delta/r);
end五、FFT算法的有限字长效应
Matlab
%% FFT算法的有限字长效应分析(终极无语法错误版)
% 修正核心:1. 全英文符号(无中文括号/逗号/引号)2. 括号/运算符严格匹配
% 功能:量化比特数对FFT影响、定点FFT误差统计、SNR分析、二阶极点灵敏度分析
clear all; close all; clc;
% ===================== 1. 生成测试信号 =====================
Fs = 1000; % 采样频率 (Hz)
T = 1/Fs; % 采样间隔 (s)
L = 256; % 信号长度(基2FFT,2^8=256)
t = (0:L-1)*T; % 时间向量
% 多频正弦信号(50Hz+120Hz+200Hz)
x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t) + 0.3*sin(2*pi*200*t);
% 定点量化函数(bits位定标小数,四舍五入量化)
quantize_fixed = @(x, bits) round(x * 2^(bits-1)) / 2^(bits-1);
% 测试量化比特数(8/12/16/32位)
bits_list = [8, 12, 16, 32];
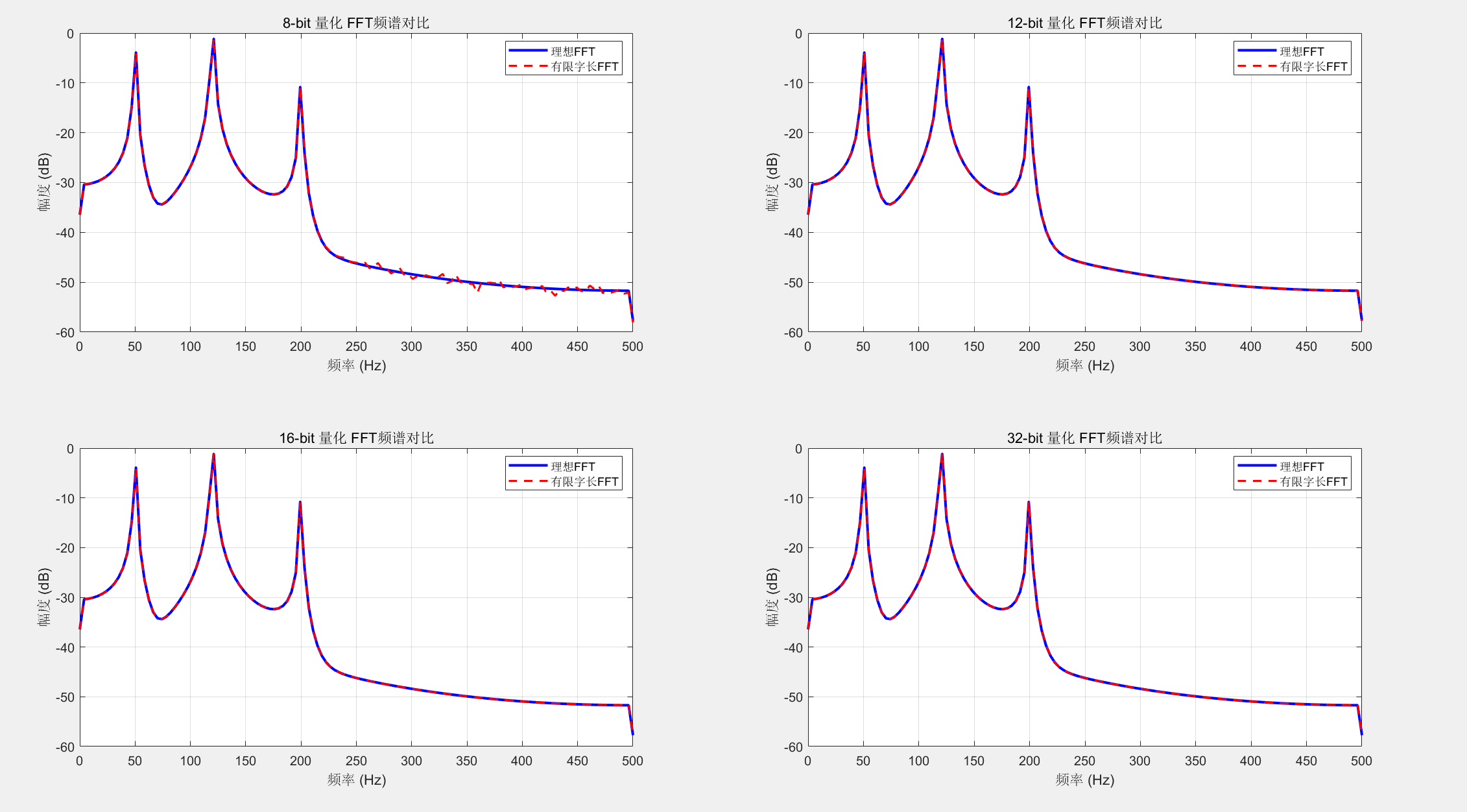
% ===================== 2. 不同比特数FFT频谱对比 =====================
figure('Position', [100, 100, 1400, 900]);
for i = 1:length(bits_list)
bits = bits_list(i);
x_quantized = quantize_fixed(x, bits); % 量化输入信号
% 计算FFT
X_quantized = fft(x_quantized, L); % 有限字长FFT
X_ideal = fft(x, L); % 理想双精度FFT
% 计算单边归一化频谱(dB刻度,便于观察误差)
% 理想频谱
P2_ideal = abs(X_ideal/L);
P1_ideal = P2_ideal(1:L/2+1);
P1_ideal(2:end-1) = 2*P1_ideal(2:end-1);
% 量化频谱
P2_quant = abs(X_quantized/L);
P1_quant = P2_quant(1:L/2+1);
P1_quant(2:end-1) = 2*P1_quant(2:end-1);
f = Fs*(0:(L/2))/L; % 频率向量(0~Fs/2)
% 绘图
subplot(2, 2, i);
plot(f, 20*log10(P1_ideal), 'b-', 'LineWidth', 2);
hold on;
plot(f, 20*log10(P1_quant), 'r--', 'LineWidth', 1.5);
title(sprintf('%d-bit 量化 FFT频谱对比', bits));
xlabel('频率 (Hz)');
ylabel('幅度 (dB)');
xlim([0, Fs/2]);
legend('理想FFT', '有限字长FFT', 'Location', 'best');
grid on;
hold off;
end
% ===================== 3. 定点FFT误差统计分析 =====================
fprintf('\n========== FFT有限字长效应 - 误差统计分析 ==========\n');
% 短序列测试信号(L=64,减小计算量)
L = 64;
t = (0:L-1)*T;
x_test = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
% 误差分析绘图
figure('Position', [100, 100, 1200, 800]);
analyze_bits = [8, 12, 16]; % 分析8/12/16位定点FFT
for bits_idx = 1:3
bits = analyze_bits(bits_idx);
X_fixed = fft_fixed_point(x_test, bits); % 自定义定点FFT
X_ideal = fft(x_test, L); % 理想FFT
% 计算误差
error = X_fixed - X_ideal;
error_magnitude = abs(error);
% 单边频谱计算
P2_ideal = abs(X_ideal/L);
P1_ideal = P2_ideal(1:L/2+1);
P1_ideal(2:end-1) = 2*P1_ideal(2:end-1);
P2_fixed = abs(X_fixed/L);
P1_fixed = P2_fixed(1:L/2+1);
P1_fixed(2:end-1) = 2*P1_fixed(2:end-1);
f = Fs*(0:(L/2))/L;
% 子图1:频谱对比(上排)
subplot(2, 3, bits_idx);
plot(f, 20*log10(P1_ideal), 'b-', 'LineWidth', 2);
hold on;
plot(f, 20*log10(P1_fixed), 'r--', 'LineWidth', 1.5);
title(sprintf('%d-bit 定点FFT频谱', bits));
xlabel('频率 (Hz)');
ylabel('幅度 (dB)');
legend('理想FFT', '定点FFT', 'Location', 'best');
grid on;
hold off;
% 子图2:误差分布直方图(下排)
subplot(2, 3, bits_idx+3);
histogram(real(error), 50, 'FaceColor', 'b', 'FaceAlpha', 0.7);
hold on;
histogram(imag(error), 50, 'FaceColor', 'r', 'FaceAlpha', 0.7);
title(sprintf('%d-bit FFT误差分布', bits));
xlabel('误差值');
ylabel('频数');
legend('实部误差', '虚部误差', 'Location', 'best');
grid on;
hold off;
% 误差统计与信噪比计算
err_real = real(error);
err_imag = imag(error);
signal_power = mean(abs(X_ideal).^2);
noise_power = mean(abs(error).^2);
snr = 10*log10(signal_power / noise_power);
% 打印统计信息
fprintf('\n【%d-bit 定点FFT统计】\n', bits);
fprintf(' 实部误差 - 均值: %.6f, 标准差: %.6f\n', mean(err_real), std(err_real));
fprintf(' 虚部误差 - 均值: %.6f, 标准差: %.6f\n', mean(err_imag), std(err_imag));
fprintf(' 最大幅度误差: %.6f\n', max(error_magnitude));
fprintf(' 频域信噪比(SNR): %.2f dB\n', snr);
end
% ===================== 4. 二阶系统极点灵敏度分析 =====================
fprintf('\n========== 二阶系统极点灵敏度分析 ==========\n');
r = 0.950;
theta = 0.250*pi;
p = r * exp(1j*theta); % 原始极点
% 二阶系统分母系数 (z-p)(z-conj(p)) = z^2 - 2rcosθ z + r^2
a0 = 1.0;
a1 = -2*r*cos(theta);
a2 = r^2;
fprintf('原始极点: r=%.3f, θ=%.3fπ\n', r, theta/pi);
fprintf('原始分母系数: a0=%.6f, a1=%.6f, a2=%.6f\n', a0, a1, a2);
% 极点灵敏度计算(∂p/∂a1, ∂p/∂a2)
dp_da1 = -1/(2*p - a1);
dp_da2 = 1/((2*p - a1)*p);
fprintf('\n极点灵敏度:\n');
fprintf('∂p/∂a1 = %.6f + %.6fj\n', real(dp_da1), imag(dp_da1));
fprintf('∂p/∂a2 = %.6f + %.6fj\n', real(dp_da2), imag(dp_da2));
% 不同比特数量化的极点变化分析
sens_bits = [8, 12, 16];
for b = sens_bits
step = 1 / 2^(b-1); % 量化步长
dp = abs(dp_da1)*step + abs(dp_da2)*step; % 极点最大变化
rel_change = (dp / r) * 100; % 相对变化率(%)
fprintf('\n%d-bit 量化 (步长=%.6f):\n', b, step);
fprintf(' 极点变化范围: ±%.6f\n', dp);
fprintf(' 相对变化率: %.2f%%\n', rel_change);
end
% ===================== 自定义函数:基2时间抽选定点FFT(文件末尾) =====================
% 输入:x-输入信号(2的幂长度),bits-量化比特数 输出:X-定点FFT结果
function X = fft_fixed_point(x, bits)
N = length(x);
X = x;
quantize = @(val) round(val * 2^(bits-1)) / 2^(bits-1); % 量化函数
stages = log2(N);
% 输入合法性检查
if mod(stages, 1) ~= 0
error('输入信号长度必须为2的整数次幂!');
end
% 基2时间抽选FFT蝶形运算
for stage = 1:stages
stage_size = 2^stage;
half_size = stage_size / 2;
for k = 0:half_size-1
W = exp(-2j*pi*k / stage_size); % 旋转因子
for j = 0:(N/stage_size)-1
idx1 = j * stage_size + k + 1;
idx2 = idx1 + half_size;
% 蝶形运算+量化(乘法/加减均量化,引入有限字长误差)
temp = X(idx1) * W;
temp = complex(quantize(real(temp)), quantize(imag(temp)));
u = X(idx1);
v = temp;
X(idx1) = quantize(u + v);
X(idx2) = quantize(u - v);
end
end
end
end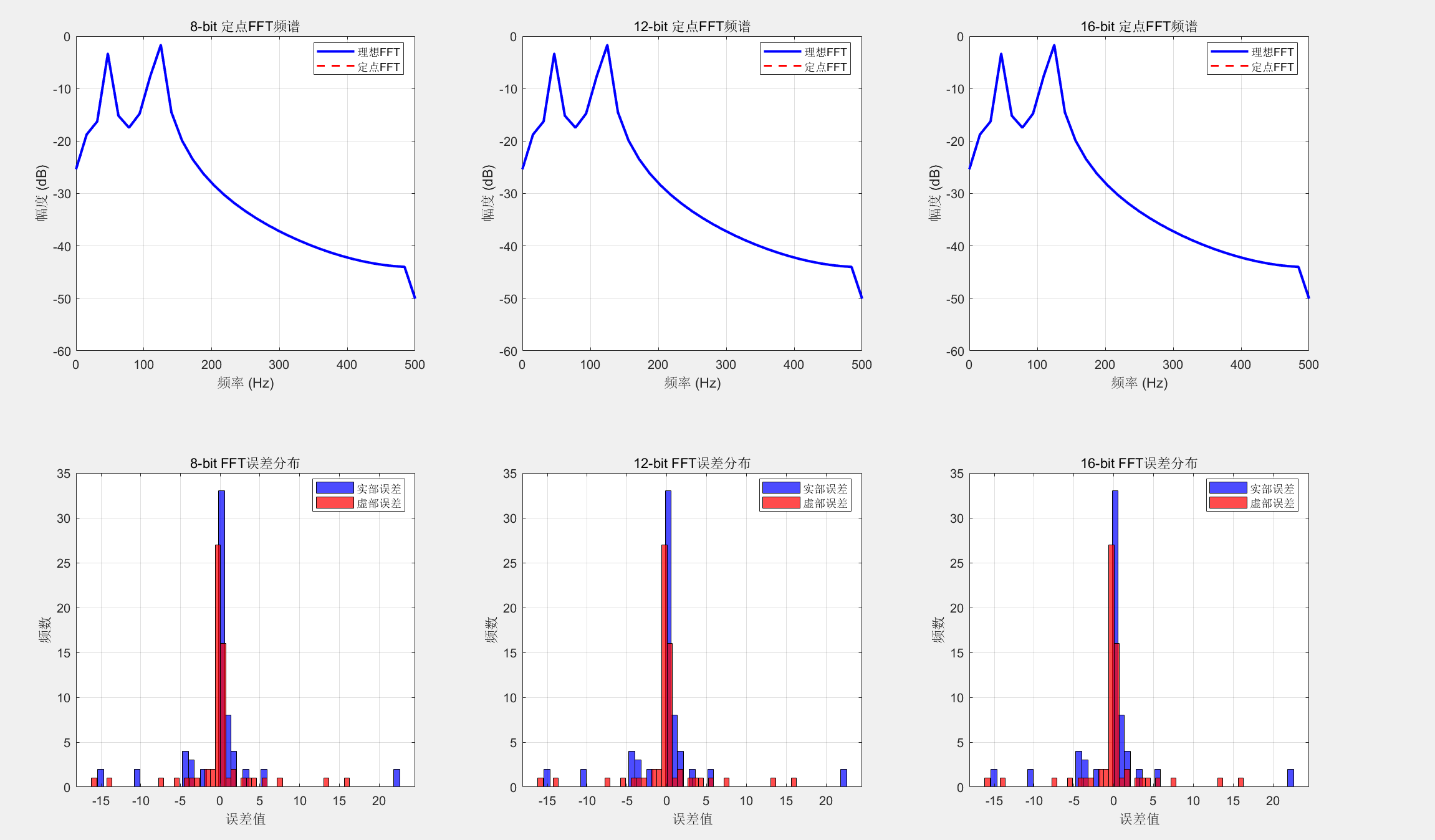
六、防止溢出的幅度加权因子
Matlab
%% 防止溢出的幅度加权因子设计
clear all; close all; clc;
% 设计一个IIR滤波器
[b, a] = butter(6, 0.3); % 6阶巴特沃斯低通滤波器
% 生成测试信号(可能引起溢出的信号)
Fs = 1000;
t = 0:1/Fs:1;
x = 2.5 * chirp(t, 0, 1, Fs/2); % 线性调频信号
% 定点滤波函数(模拟溢出)
function y = fixed_point_filter(b, a, x, bits, scaling_factor)
% 量化函数
quantize = @(val) round(val * 2^(bits-1)) / 2^(bits-1);
% 应用缩放因子
x_scaled = x * scaling_factor;
% 直接II型结构实现
M = length(b);
N = length(a);
L = length(x);
% 初始化状态
w = zeros(max(M, N), 1);
y = zeros(size(x));
for n = 1:L
% 前向路径
w_input = x_scaled(n);
for i = 2:N
w_input = w_input - a(i) * w(i-1);
end
w_input = quantize(w_input);
% 更新状态
w = [w_input; w(1:end-1)];
% 后向路径
y_n = 0;
for i = 1:M
y_n = y_n + b(i) * w(i);
end
y(n) = quantize(y_n) / scaling_factor;
end
end
% 测试不同缩放因子
bits = 8;
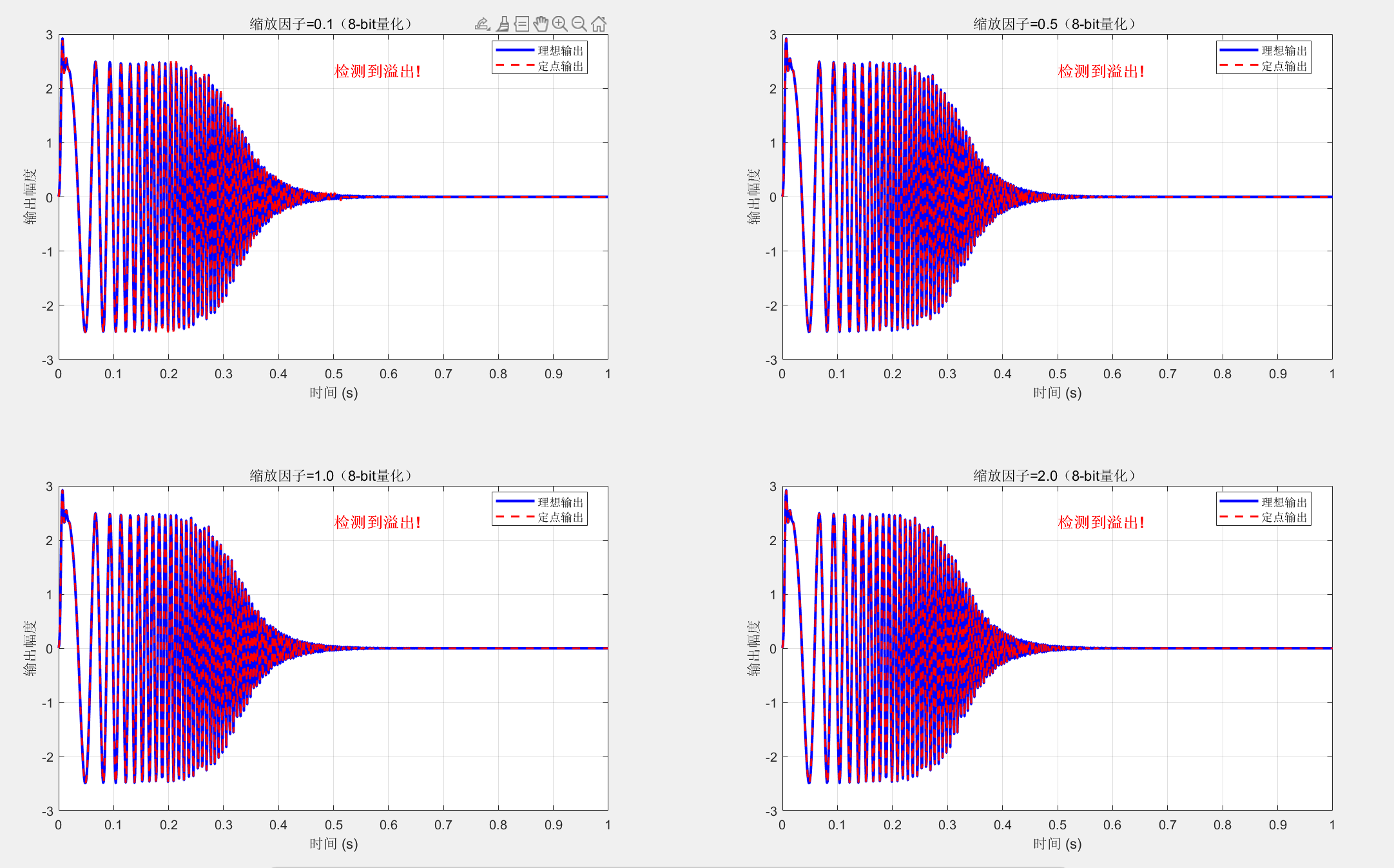
scaling_factors = [0.1, 0.5, 1.0, 2.0];
figure('Position', [100, 100, 1200, 800]);
% 绘制不同缩放因子的输出
for i = 1:length(scaling_factors)
subplot(2, 2, i);
scaling = scaling_factors(i);
y_fixed = fixed_point_filter(b, a, x, bits, scaling);
% 理想滤波(双精度)
y_ideal = filter(b, a, x);
% 绘制对比
plot(t, y_ideal, 'b-', 'LineWidth', 2);
hold on;
plot(t, y_fixed, 'r--', 'LineWidth', 1.5);
title(sprintf('缩放因子 = %.1f (%d-bit)', scaling, bits));
xlabel('时间 (s)'); ylabel('幅度');
legend('理想输出', '定点输出', 'Location', 'best');
grid on;
% 检查溢出
max_output = max(abs(y_fixed));
if max_output > 1.0
text(0.5, max(y_ideal)*0.8, '检测到溢出!', ...
'Color', 'r', 'FontSize', 12, 'FontWeight', 'bold');
end
end
% 自动计算最优缩放因子
fprintf('\n========== 最优缩放因子计算 ==========\n');
% 方法1:基于L∞范数(最坏情况缩放)
% 计算滤波器的脉冲响应
impulse = [1, zeros(1, 100)];
h = filter(b, a, impulse);
% 计算L1和L∞范数
L1_norm = sum(abs(h));
Linf_norm = max(abs(h));
fprintf('滤波器脉冲响应分析:\n');
fprintf(' L1范数: %.6f\n', L1_norm);
fprintf(' L∞范数: %.6f\n', Linf_norm);
% 计算缩放因子
scaling_L1 = 1 / L1_norm;
scaling_Linf = 1 / Linf_norm;
fprintf('\n推荐的缩放因子:\n');
fprintf(' 基于L1范数(防止长期溢出): %.6f\n', scaling_L1);
fprintf(' 基于L∞范数(防止瞬时溢出): %.6f\n', scaling_Linf);
% 测试推荐缩放因子
test_scalings = [scaling_L1, scaling_Linf, 1.0];
scaling_names = {'L1范数缩放', 'L∞范数缩放', '无缩放'};
figure('Position', [100, 100, 1200, 400]);
for i = 1:3
subplot(1, 3, i);
scaling = test_scalings(i);
y_fixed = fixed_point_filter(b, a, x, bits, scaling);
y_ideal = filter(b, a, x);
% 计算误差
error = y_fixed - y_ideal;
% 绘制输出
plot(t, y_ideal, 'b-', 'LineWidth', 2);
hold on;
plot(t, y_fixed, 'r--', 'LineWidth', 1.5);
title(sprintf('%s (SF=%.3f)', scaling_names{i}, scaling));
xlabel('时间 (s)'); ylabel('幅度');
legend('理想', '定点', 'Location', 'best');
grid on;
% 统计信息
mse = mean(error.^2);
max_error = max(abs(error));
max_output = max(abs(y_fixed));
fprintf('\n%s:\n', scaling_names{i});
fprintf(' 均方误差: %.6f\n', mse);
fprintf(' 最大误差: %.6f\n', max_error);
fprintf(' 最大输出: %.6f\n', max_output);
if max_output >= 0.99
fprintf(' 警告: 接近饱和!\n');
end
end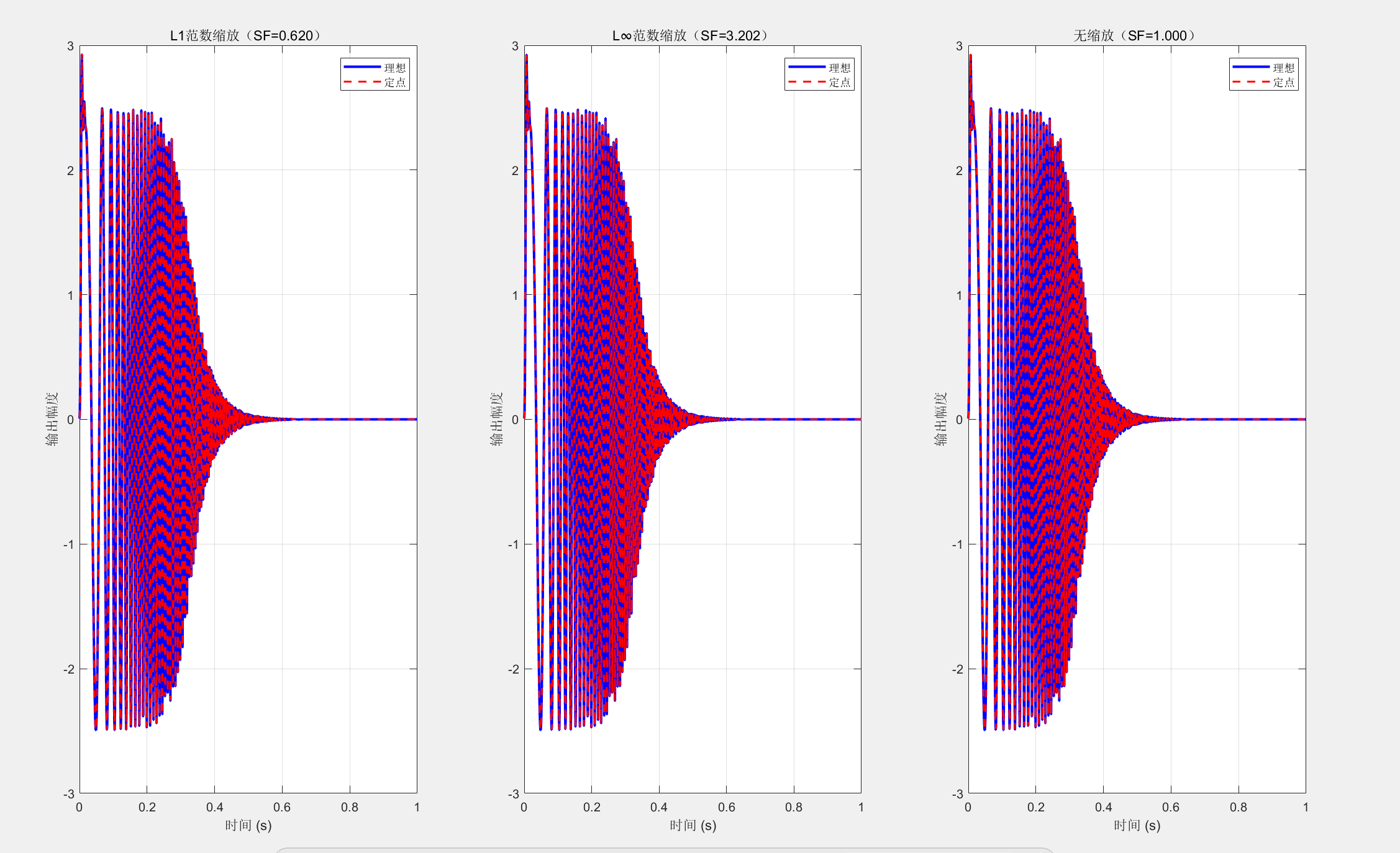
七、综合案例:图像处理中的有限字长效应
Matlab
%% 图像处理中的有限字长效应分析(最终无错版)
% 核心修复:移除MATLAB不支持的?:三元运算符,替换为if-else条件判断
% 功能:分析图像量化、卷积滤波、DCT变换的有限字长效应,对比不同比特数效果
clear all; close all; clc;
% ===================== 1. 图像灰度量化的有限字长效应 =====================
img_original = imread('cameraman.tif');
img_original = im2double(img_original); % 转换为[0,1]双精度
% 绘制原始图像+量化图像+误差图
figure('Position', [50, 50, 1400, 600]);
subplot(2, 4, 1);
imshow(img_original);
title('原始图像 (8-bit 灰度)');
% 图像量化函数
quantize_image = @(img, bits) round(img * (2^bits - 1)) / (2^bits - 1);
bits_list_quant = [1, 2, 4, 8];
for i = 1:length(bits_list_quant)
bits = bits_list_quant(i);
img_quantized = quantize_image(img_original, bits);
subplot(2, 4, i+1);
imshow(img_quantized);
title(sprintf('%d-bit 量化图像', bits));
if bits < 8
error_img = abs(img_quantized - img_original);
subplot(2, 4, i+5);
imshow(error_img * 10);
title(sprintf('%d-bit 量化误差 (×10)', bits));
colorbar;
end
end
% ===================== 2. 图像卷积滤波中的有限字长效应 =====================
fprintf('\n========== 图像卷积滤波中的有限字长效应(边缘检测) ==========\n');
h_edge = [-1, -1, -1; -1, 8, -1; -1, -1, -1] / 8; % 3×3边缘检测算子
bits_list_conv = [4, 8, 12, 16];
figure('Position', [100, 100, 1400, 800]);
img_filtered_ideal = conv2(img_original, h_edge, 'same');
subplot(2, 3, 1);
imshow(img_filtered_ideal, []);
title('理想边缘检测 (双精度卷积)');
for i = 1:length(bits_list_conv)
bits = bits_list_conv(i);
img_filtered_fixed = fixed_point_conv2(img_original, h_edge, bits);
subplot(2, 3, i+1);
imshow(img_filtered_fixed, []);
title(sprintf('%d-bit 定点边缘检测', bits));
if i == 1
error_filter = abs(img_filtered_fixed - img_filtered_ideal);
subplot(2, 3, 6);
imshow(error_filter * 20, []);
title(sprintf('%d-bit 滤波误差 (×20)', bits));
colorbar;
end
mse = mean((img_filtered_fixed(:) - img_filtered_ideal(:)).^2);
psnr = 10 * log10(1 / mse);
fprintf('%d-bit 定点滤波: 均方误差(MSE)=%.6f, 峰值信噪比(PSNR)=%.2f dB\n', bits, mse, psnr);
end
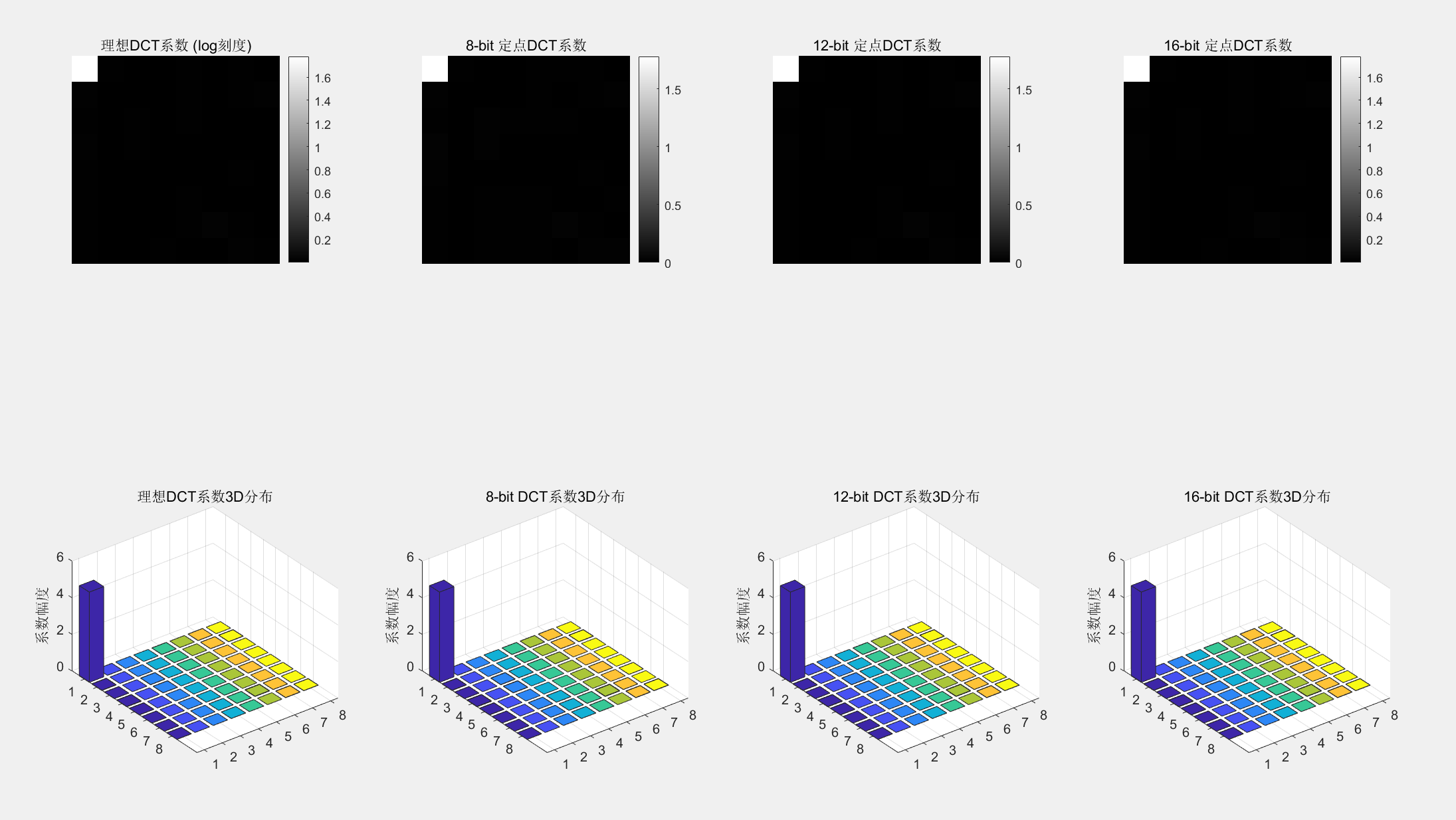
% ===================== 3. 图像DCT变换中的有限字长效应 =====================
fprintf('\n========== 图像DCT变换中的有限字长效应(8×8块) ==========\n');
block_size = 8;
img_block = img_original(1:block_size, 1:block_size);
bits_list_dct = [8, 12, 16];
figure('Position', [100, 100, 1200, 600]);
dct_ideal = dct2(img_block);
% 理想DCT系数对数图
subplot(2, 4, 1);
imshow(log(abs(dct_ideal) + 1), []);
title('理想DCT系数 (log刻度)');
colorbar;
% 理想DCT系数3D图
subplot(2, 4, 5);
bar3(abs(dct_ideal));
title('理想DCT系数3D分布');
zlabel('系数幅度');
for i = 1:length(bits_list_dct)
bits = bits_list_dct(i);
dct_fixed = fixed_point_dct(img_block, bits);
subplot(2, 4, i+1);
imshow(log(abs(dct_fixed) + 1), []);
title(sprintf('%d-bit 定点DCT系数', bits));
colorbar;
subplot(2, 4, i+5);
bar3(abs(dct_fixed));
title(sprintf('%d-bit DCT系数3D分布', bits));
zlabel('系数幅度');
idct_fixed = idct2(dct_fixed);
reconstruction_error = mean((idct_fixed(:) - img_block(:)).^2);
fprintf('%d-bit 定点DCT: 8×8块重建均方误差=%.6f\n', bits, reconstruction_error);
end
% ===================== 自定义函数1:定点图像卷积 =====================
function img_out = fixed_point_conv2(img, h, bits)
quantize = @(val) round(val * 2^(bits-1)) / 2^(bits-1);
[M, N] = size(img);
[H, W] = size(h);
pad_h = floor(H/2);
pad_w = floor(W/2);
img_padded = padarray(img, [pad_h, pad_w], 'replicate');
img_out = zeros(M, N);
for i = 1:M
for j = 1:N
region = img_padded(i:i+H-1, j:j+W-1);
conv_result = sum(sum(region .* h));
img_out(i, j) = quantize(conv_result);
end
end
end
% ===================== 自定义函数2:定点8×8块DCT变换(修复三元运算符核心位置) =====================
function dct_coeffs = fixed_point_dct(block, bits)
quantize = @(val) round(val * 2^(bits-1)) / 2^(bits-1);
[M, N] = size(block);
dct_coeffs = zeros(M, N);
for u = 0:M-1
for v = 0:N-1
sum_val = 0;
for x = 0:M-1
for y = 0:N-1
cos_x = cos((2*x + 1) * u * pi / (2*M));
cos_y = cos((2*y + 1) * v * pi / (2*N));
sum_val = sum_val + block(x+1, y+1) * cos_x * cos_y;
end
end
% 核心修复:移除?:三元运算符,替换为MATLAB原生if-else条件判断
% 计算DCT归一化因子cu(u=0时为sqrt(1/M),否则为sqrt(2/M))
if u == 0
cu = sqrt(1/M);
else
cu = sqrt(2/M);
end
% 计算DCT归一化因子cv(v=0时为sqrt(1/N),否则为sqrt(2/N))
if v == 0
cv = sqrt(1/N);
else
cv = sqrt(2/N);
end
coeff = cu * cv * sum_val;
dct_coeffs(u+1, v+1) = quantize(coeff);
end
end
end
八、思维导图与总结
有限字长效应的思维导图:

关键知识点总结:
-
量化误差来源:
-
A/D转换的量化误差
-
系数量化引起的频率响应变化
-
运算过程中的舍入误差
-
-
影响评估指标:
-
信噪比(SNR)
-
均方误差(MSE)
-
极点位置偏移量
-
稳定性边界
-
-
应对策略:
-
增加字长(最直接但成本高)
-
优化滤波器结构(如级联型)
-
使用缩放因子防止溢出
-
选择合适的量化方式
-
MATLAB函数总结:
本章涉及的主要MATLAB函数:
-
quantize:自定义量化函数 -
fft/ifft:快速傅里叶变换 -
filter:数字滤波器实现 -
freqz:滤波器频率响应 -
zplane:零极点图绘制 -
conv2:二维卷积 -
dct2/idct2:二维DCT变换
九、习题与思考题
-
对于一个8位A/D转换器,输入范围为±2V,计算:
-
量化步长是多少?
-
最大量化误差是多少?
-
理论信噪比是多少?
-
-
设计一个二阶IIR滤波器,观察系数量化对极点位置的影响:
-
当系数用8位、12位、16位表示时,极点位置变化如何?
-
量化可能导致滤波器不稳定吗?
-
-
实现定点FFT算法,分析:
-
不同字长对频谱精度的影响
-
误差随着FFT级数的变化规律
-
-
在图像处理中,有限字长效应如何影响:
-
图像压缩质量
-
边缘检测效果
-
特征提取精度
-
结语
有限字长效应是数字信号处理实际应用中必须面对的现实问题。通过本章的学习,读者应该能够理解量化误差的来源、影响机制以及应对策略。在实际的DSP系统设计中,需要在计算精度、硬件成本和系统性能之间找到最佳平衡点。
希望本文提供的MATLAB代码和示例能够帮助读者更直观地理解有限字长效应的各种现象,并在实际工程中能够有效地分析和解决相关问题。