目录
[1. 时间复杂度分析](#1. 时间复杂度分析)
[2. 空间复杂度分析](#2. 空间复杂度分析)
一、冒泡排序思想
冒泡排序的核⼼思想就是:两两相邻的元素进⾏⽐较,元素 小 / 大 就交换,然后进行下一个两两相邻的元素进⾏⽐较,重复以上动作,直到 升序 / 降序。
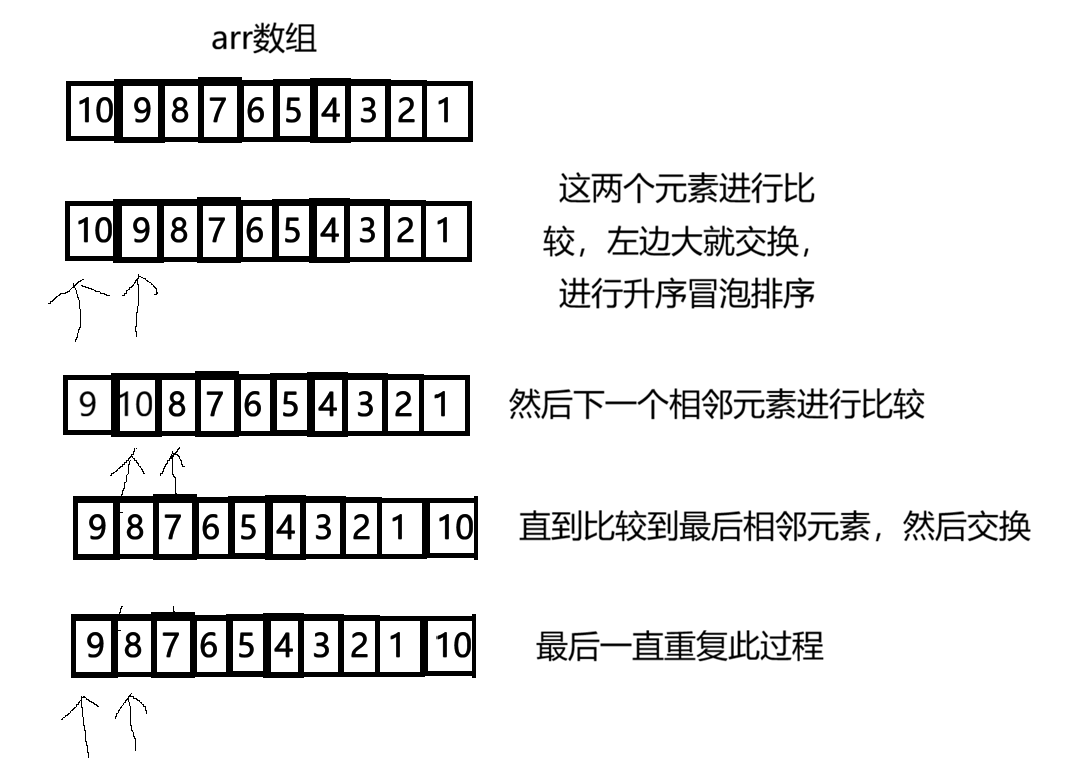
二、冒泡排序代码
cpp
#include<stdio.h>
void bubble_sort(int* arr, int sz) {
int i = 0;
for (i = 0; i < sz - 1; i++) {
int j = 0;
int flag = 1;
for (j = 0; j < sz - 1 - i; j++) {
if (arr[j] > arr[j+1]) {
int tmp = 0;
tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flag = 0;
}
}
if (flag) {
break;
}
}
}
int main() {
int arr[] = { 10,9,8,7,6,5,4,3,2,1 };
int sz = sizeof(arr) / sizeof(arr[0]);
bubble_sort(arr, sz);
for (int i = 0; i < sz; i++) {
printf("%d ", arr[i]);
}
return 0;
}进行升序排序,如图:

三、冒泡排序时间复杂度与空间复杂度
1. 时间复杂度分析
冒泡排序的核心操作是 比较 和 交换。我们通过嵌套循环来实现:
外层循环:控制排序的"轮数"。对于 n 个元素,最多需要 n-1 轮才能确保完全有序。
内层循环:在每一轮中,对未排序部分的相邻元素进行两两比较,并根据需要交换位置。
时间复杂度我们只讨论最坏情况:
当需要排序成升序的数组完全是逆序的时,每一轮都需要进行最大次数的比较和交换。
比较次数 = (n-1) + (n-2) + ... + 2 + 1 = n(n-1)/2
交换次数同样约为 n(n-1)/2。
因此,总操作次数与 n² 成正比,时间复杂度为O(n²)。
2. 空间复杂度分析
冒泡排序的整个排序过程只在原数组内部进行。除了使用几个固定的临时变量(如用于交换的 tmp、循环计数器 i, j、判断是否已经 升序 / 降序 的flag)外,不需要申请额外的、与数据规模 n 相关的存储空间。
所以无论数组有多大,这些临时变量的数量都是固定的。因此,冒泡排序的空间复杂度为 O(1)。