SLAM文献之A micro Lie theory for state estimation in robotic（2）

II. 微型李理论（A Micro Lie Theory）

F. 共轭作用（Adjoint）与共轭矩阵

如果我们在公式 (25, 27) 中将 Y Y Y 识别出来，可以得到

E τ ⊕ X = X ⊕ X τ ^E\tau \oplus X = X \oplus ^X\tau Eτ⊕X=X⊕Xτ

这确定了局部与全局切向量之间的关系（见图 7）。结合公式 (20, 25, 27)，我们可以写为

Exp ( E τ ) X = X Exp ( X τ ) \text{Exp}(^E\tau) X = X \text{Exp}(^X\tau) Exp(Eτ)X=XExp(Xτ)

exp ⁡ ( E τ ∧ ) = X exp ⁡ ( X τ ∧ ) X − 1 = exp ⁡ ( X X τ ∧ X − 1 ) \exp(E\tau^\wedge) = X \exp(^X\tau^\wedge) X^{-1} = \exp(X ^X\tau^\wedge X^{-1}) exp(Eτ∧)=Xexp(Xτ∧)X−1=exp(XXτ∧X−1)

E τ ∧ = X X τ ∧ X − 1 ^E\tau^\wedge = X ^X\tau^\wedge X^{-1} Eτ∧=XXτ∧X−1

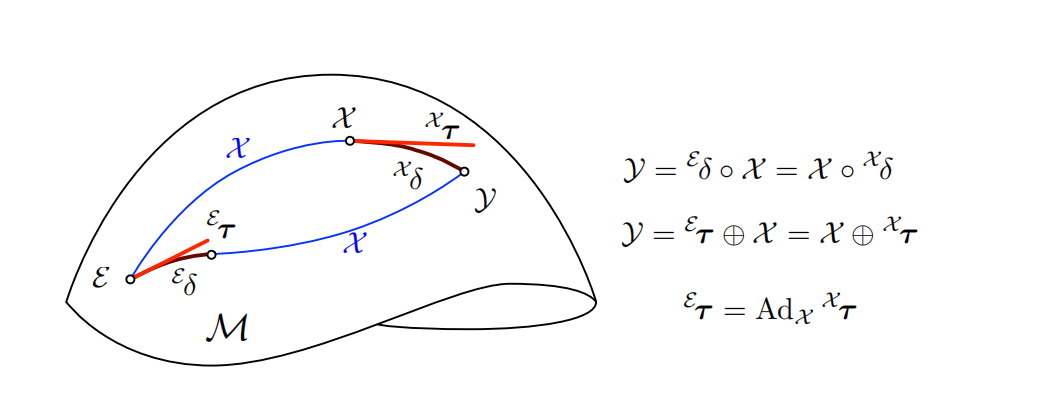
图 7 ：两条路径 X ∘ δ X X \circ ^X_\delta X∘δX 和 δ E ∘ X ^E_\delta \circ X δE∘X 都将原点 E E E 连接到点 Y Y Y 。这两条路径都是将元素 X X X 与增量（或称为"delta"）进行复合，只是这些增量分别在局部坐标系 中表示为 δ X ^X_\delta δX ，或在原点坐标系 中表示为 δ E ^E_\delta δE 。由于群运算的非交换性 ，元素 δ X ^X_\delta δX 与 δ E ^E_\delta δE 并不相等。因此，它们对应的切向量 τ X = log ⁡ ( δ X ) ^X_\tau = \log(^X_\delta) τX=log(δX) 和 τ E = log ⁡ ( δ E ) ^E_\tau = \log(^E_\delta) τE=log(δE) 也不相等。二者之间通过如下线性变换相关联：

τ E = Ad ⁡ X X τ ^E_\tau = \operatorname{Ad}X ^X\tau τE=AdXXτ

其中，Ad ⁡ X \operatorname{Ad}_X AdX 是流形 M M M 在点 X X X 处的伴随算子（adjoint）。

共轭作用（Adjoint） ：
我们定义 Lie 群 M M M 在 X X X 点的共轭作用，记作 Ad X \text{Ad}_X AdX，为

Ad X : m → m ; τ ∧ ↦ Ad X ( τ ∧ ) ≜ X τ ∧ X − 1 , (29) \text{Ad}_X : m \to m; \quad \tau^\wedge \mapsto \text{Ad}_X(\tau^\wedge) \triangleq X \tau^\wedge X^{-1}\tag{29}, AdX:m→m;τ∧↦AdX(τ∧)≜Xτ∧X−1,(29)

从而有

E τ ∧ = Ad X ( X τ ∧ ) ^E\tau^\wedge = \text{Ad}_X(^X\tau^\wedge) Eτ∧=AdX(Xτ∧)

这定义了群对自身李代数的共轭作用。共轭作用具有两个有趣且易于证明的性质：

线性性 ：
Ad X ( a τ ∧ + b σ ∧ ) = a Ad X ( τ ∧ ) + b Ad X ( σ ∧ ) \text{Ad}_X(a\tau^\wedge + b\sigma^\wedge) = a \text{Ad}_X(\tau^\wedge) + b \text{Ad}_X(\sigma^\wedge) AdX(aτ∧+bσ∧)=aAdX(τ∧)+bAdX(σ∧)
同态性 ：
Ad X ( Ad y ( τ ∧ ) ) = Ad x y ( τ ∧ ) \text{Ad}_X(\text{Ad}y(\tau^\wedge)) = \text{Ad}{xy}(\tau^\wedge) AdX(Ady(τ∧))=Adxy(τ∧)

共轭矩阵（Adjoint Matrix） ：
由于 Ad X ( ) \text{Ad}_X() AdX() 是线性的，我们可以找到一个等价的矩阵算子 Ad X \text{Ad}_X AdX，将笛卡尔切向量 E τ ∼ E τ ∧ ^E\tau \sim ^E\tau^\wedge Eτ∼Eτ∧ 和 X τ ∼ X τ ∧ ^X\tau \sim ^X\tau^\wedge Xτ∼Xτ∧ 映射为

Ad X : R m → R m ; X τ ↦ E τ = Ad X X τ , (30) \text{Ad}_X : \mathbb{R}^m \to \mathbb{R}^m; \quad X\tau \mapsto ^E\tau = \text{Ad}_X X\tau,\tag{30} AdX:Rm→Rm;Xτ↦Eτ=AdXXτ,(30)

我们称之为共轭矩阵 。它可以通过对公式 (29) 应用 ∨ \vee ∨ 运算计算，即

Ad X τ = ( X τ ∧ X − 1 ) ∨ , (31) \text{Ad}_X \tau = (X \tau^\wedge X^{-1})^\vee,\tag{31} AdXτ=(Xτ∧X−1)∨,(31)

然后展开右边表达式以识别共轭矩阵（见例 6 及附录）。共轭矩阵还具有以下性质：

X ⊕ τ = ( Ad X τ ) ⊕ X (32) X \oplus \tau = (\text{Ad}_X \tau) \oplus X \tag{32} X⊕τ=(AdXτ)⊕X(32)

Ad X − 1 = A d ( X ) − 1 (33) \text{Ad}_{X^{-1}} = Ad(\text{}_X)^{-1}\tag{33} AdX−1=Ad(X)−1(33)

Ad X Y = Ad X Ad Y (34) \text{Ad}_{XY} = \text{Ad}_X \text{Ad}_Y\tag{34} AdXY=AdXAdY(34)

注意在公式 (33, 34) 中，等式左边通常比右边计算代价低。我们将经常使用共轭矩阵将切空间中 X X X 点的向量线性映射到原点的切空间向量，即

E τ = Ad X X τ . ^E\tau = \text{Ad}_X X\tau. Eτ=AdXXτ.

在本工作中，共轭矩阵将简化称为共轭。

示例 6：SE(3) 的共轭矩阵（Adjoint Matrix）

刚体运动群 S E ( 3 ) \mathrm{SE}(3) SE(3)（见附录 D）具有如下群元素、李代数元素以及向量表示：

M = [ R t 0 1 ] , τ ∧ = [ [ θ ] × ρ 0 0 ] , τ = [ ρ θ ] . M = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix}, \qquad \tau^\wedge = \begin{bmatrix} [\theta]_\times & \rho \\ 0 & 0 \end{bmatrix}, \qquad \tau = \begin{bmatrix} \rho \\ \theta \end{bmatrix}. M=[R0t1],τ∧=[[θ]×0ρ0],τ=[ρθ].

根据公式 (31)，共轭矩阵可通过展开得到：

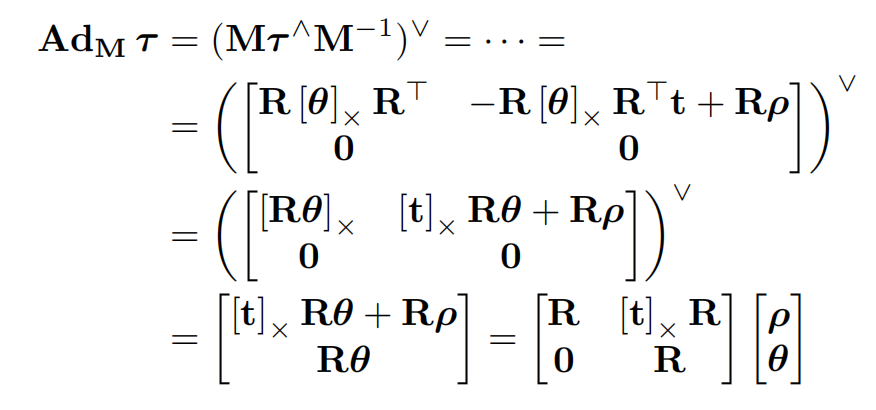
利用恒等式

$R θ \] × = R \[ θ \] × R ⊤ \[R\\theta\]\\times = R \[\\theta\]\\times R\^\\top \[Rθ\]×=R\[θ\]×R⊤$

继续化简,最终，共轭矩阵为：

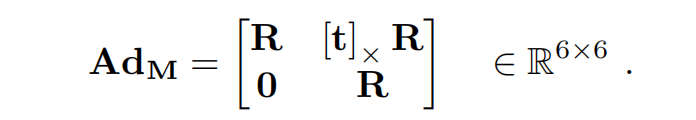
G. 李群上的导数（Derivatives on Lie Groups）

在李群背景下定义导数有多种方式，我们在此专注于以雅可比矩阵（Jacobian）形式定义的、映射向量切空间之间的导数。这已经足够，因为在这些空间中可以方便地定义不确定性和增量。利用这些 Jacobian，李群上的不确定性管理公式在形式上将与向量空间中的非常相似。

接下来描述的 Jacobian 满足链式法则，因此我们可以通过求逆、群运算（composition）、指数映射（exp）、李群作用（action）等部分 Jacobian 很容易组合得到任意 Jacobian（详见第三节 A 的证明）。

1) 回顾：向量空间上的 Jacobians

对一个多变量函数
f : R m → R n f: \mathbb{R}^m \rightarrow \mathbb{R}^n f:Rm→Rn，

其 Jacobian 是一个 n × m n\times m n×m 的矩阵，包含所有偏导数：

J = ∂ f ( x ) ∂ x = [ ∂ f 1 ∂ x 1 ⋯ ∂ f 1 ∂ x m ⋮ ⋱ ⋮ ∂ f n ∂ x 1 ⋯ ∂ f n ∂ x m ] ∈ R n × m . (35) J = \frac{\partial f(x)}{\partial x} = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_m} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial x_1} & \cdots & \frac{\partial f_n}{\partial x_m} \end{bmatrix} \in \mathbb{R}^{n \times m}. \tag{35} J=∂x∂f(x)= ∂x1∂f1⋮∂x1∂fn⋯⋱⋯∂xm∂f1⋮∂xm∂fn ∈Rn×m.(35)

将 J = [ j 1 ⋯ j m ] J = [j_1 \ \cdots\ j_m] J=[j1 ⋯ jm] 列分块，其中第 i i i 列向量为

j i = ∂ f ( x ) ∂ x i ≜ lim ⁡ h → 0 f ( x + h e i ) − f ( x ) h ∈ R n , (36) j_i = \frac{\partial f(x)}{\partial x_i} \triangleq \lim_{h \to 0} \frac{f(x + h e_i) - f(x)}{h} \in \mathbb{R}^n , \tag{36} ji=∂xi∂f(x)≜h→0limhf(x+hei)−f(x)∈Rn,(36)

其中 e i e_i ei 是 R m \mathbb{R}^m Rm 的第 i i i 个标准基向量。

注意分子中的向量：

v i ( h ) = f ( x + h e i ) − f ( x ) ∈ R n (37) v_i(h) = f(x + h e_i) - f(x) \in \mathbb{R}^n \tag{37} vi(h)=f(x+hei)−f(x)∈Rn(37)

表示沿方向 e i e_i ei 的扰动导致的 f ( x ) f(x) f(x) 的变化，因此 j i = ∂ v i ( h ) / ∂ h ∣ h = 0 j_i = \partial v_i(h) / \partial h |_{h=0} ji=∂vi(h)/∂h∣h=0。

为方便起见，引入紧凑写法：

J = ∂ f ( x ) ∂ x ≜ lim ⁡ h → 0 f ( x + h ) − f ( x ) h ∈ R n × m , (38) J = \frac{\partial f(x)}{\partial x} \triangleq \lim_{h\to 0} \frac{f(x+h)-f(x)}{h} \in \mathbb{R}^{n\times m}, \tag{38} J=∂x∂f(x)≜h→0limhf(x+h)−f(x)∈Rn×m,(38)

其中 h ∈ R m h \in \mathbb{R}^m h∈Rm。需注意，这只是符号简化，因为不能真正对向量 h h h 做除法；实际计算仍依赖式 (36)。然而，通过将分子展开成关于 h h h 的线性项并识别 Jacobian，可使用以下机制：

lim ⁡ h → 0 f ( x + h ) − f ( x ) h = ⋯ = lim ⁡ h → 0 J h h ≜ ∂ ( J h ) ∂ h = J . (39) \lim_{h\to 0} \frac{f(x+h)-f(x)}{h} = \cdots = \lim_{h\to 0} \frac{J h}{h}\triangleq \qquad \frac{\partial (J h)}{\partial h} = J . \tag{39} h→0limhf(x+h)−f(x)=⋯=h→0limhJh≜∂h∂(Jh)=J.(39)

最终，在 h h h 足够小时，有线性近似：

f ( x + h ) → h → 0 f ( x ) + ∂ f ( x ) ∂ x h . (40) f(x+h) \xrightarrow[h\to 0]{} f(x) + \frac{\partial f(x)}{\partial x} h . \tag{40} f(x+h) h→0f(x)+∂x∂f(x)h.(40)

2) 李群上的右 Jacobian（Right Jacobians）

受标准导数定义 (38) 启发，我们使用右侧的 ⊕ \oplus ⊕ 和 ⊖ \ominus ⊖（论文中符号为 ⊕ 和 "minus"）来定义作用于李群间函数
f : M → N f : M \rightarrow N f:M→N 的 Jacobian（见图 8）。

将 (38) 中的 + , − {+, -} +,− 替换为 ⊕ , ⊖ {\oplus, \ominus} ⊕,⊖ 可得类似标准导数的定义：

X D f ( X ) ≜ D f ( X ) D X lim ⁡ τ → 0 f ( X ⊕ τ ) ⊖ f ( X ) τ ∈ R n × m . (41a) {^{X}} D f(X) \triangleq \frac{D f(X)}{D X} \lim_{\tau \to 0} \frac{f(X \oplus \tau)\ \ominus\ f(X)}{\tau} \in \mathbb{R}^{n \times m}. \tag{41a} XDf(X)≜DXDf(X)τ→0limτf(X⊕τ) ⊖ f(X)∈Rn×m.(41a)

其展开形式为：

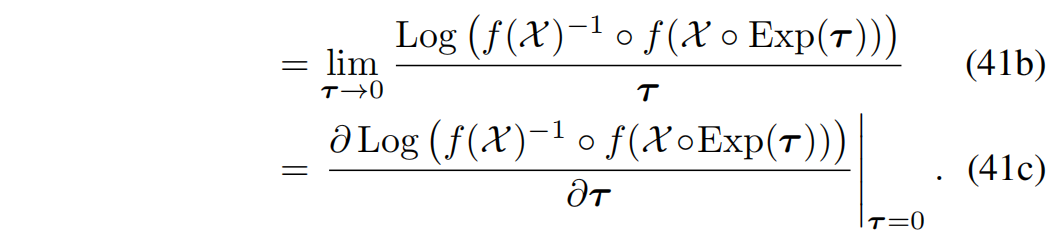
我们将这个雅可比称为 f f f 的右雅可比（right Jacobian） 。注意，式 (41c) 本质上只是对一个相当复杂的函数的标准导数（见式 (38)）：

g ( τ ) = Log ⁡ ( f ( X ) − 1 ∘ f ( X ∘ Exp ⁡ ( τ ) ) ) g(\tau) = \operatorname{Log}\left( f(X)^{-1} \circ f\left( X \circ \operatorname{Exp}(\tau) \right) \right) g(τ)=Log(f(X)−1∘f(X∘Exp(τ)))

而将其写成式 (41a) 的形式则更具直观意义 ：它表示的是 f ( X ) f(X) f(X) 对 X X X 的导数 ，只不过我们将无穷小变化表示在切空间中 而已！确实，得益于右加运算 ⊕ \oplus ⊕ 和 ⊖ \ominus ⊖ 的定义方式， X X X 和 f ( X ) f(X) f(X) 的变化现在都被表示为局部切空间中的向量 ，也就是说，分别位于
X ∈ M X \in \mathcal{M} X∈M 处的切空间 T X M T_X\mathcal{M} TXM，以及 f ( X ) ∈ N f(X) \in \mathcal{N} f(X)∈N 处的切空间 T f ( X ) N T_{f(X)}\mathcal{N} Tf(X)N。

因此，这个导数就是一个真正意义上的雅可比矩阵
R ∈ R n × m \mathbf{R} \in \mathbb{R}^{n \times m} R∈Rn×m

它以线性的方式映射局部切空间：
T X M ⟶ T f ( X ) N T_X\mathcal{M} \longrightarrow T_{f(X)}\mathcal{N} TXM⟶Tf(X)N

（我们用带有局部上标 X X X 的方式来标记这个导数）。

就像在向量空间中一样，这个矩阵的每一列都对应一个方向导数。也就是说，向量

σ i ( h ) = f ( X ⊕ h e i ) ⊖ f ( X ) ∈ R n (42) \sigma_i(h) = f(X \oplus h e_i) \ominus f(X) \in \mathbb{R}^n \tag{42} σi(h)=f(X⊕hei)⊖f(X)∈Rn(42)

（再次参见图 8，并将式 (42) 中的 σ i \sigma_i σi 与式 (37) 中的 v i v_i vi 进行对比）表示的是：当 X X X 沿着方向 e i e_i ei 发生变化时， f ( X ) f(X) f(X) 的变化量。

其对应的雅可比矩阵列向量为
j i = ∂ σ i ( h ) ∂ h ∣ h = 0 . \mathbf{j}i = \left.\frac{\partial \sigma_i(h)}{\partial h}\right|{h=0}. ji=∂h∂σi(h) h=0.

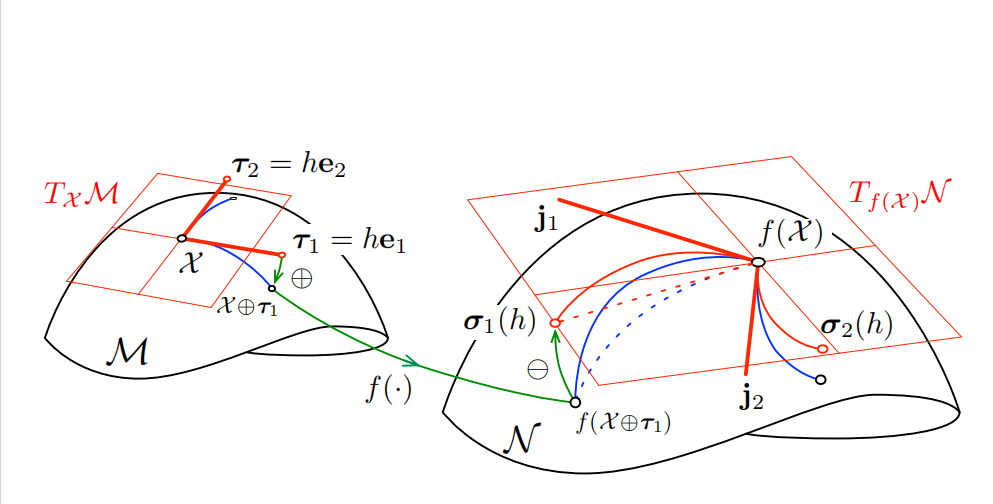
图 8. 函数 f : M → N f:\mathcal{M}\rightarrow\mathcal{N} f:M→N 的右雅可比（Right Jacobian）示意图。

沿着规范方向的扰动向量
τ i = h e i ∈ T X M \tau_i = h e_i \in T_X\mathcal{M} τi=hei∈TXM

通过 加法（ ⊕ \oplus ⊕）→ 应用 f ( ⋅ ) f(\cdot) f(⋅) → 减法（ ⊖ \ominus ⊖） 的过程（绿色箭头），被传播为
σ i ∈ T f ( X ) N , \sigma_i \in T_{f(X)}\mathcal{N}, σi∈Tf(X)N,

从而得到
σ i ( h ) = f ( X ⊕ h e i ) ⊖ f ( X ) . \sigma_i(h) = f(X \oplus h e_i) \ominus f(X). σi(h)=f(X⊕hei)⊖f(X).

当 h h h 取不同数值时，请注意：在流形 M \mathcal{M} M 中，扰动
τ i ( h ) = h e i \tau_i(h) = h e_i τi(h)=hei

（粗红线）沿着测地线（回顾图 1）在 M \mathcal{M} M 上生成一条路径（蓝线）。同时还应注意，在流形 N \mathcal{N} N 中，由于函数 f ( ⋅ ) f(\cdot) f(⋅) 的非线性 ，其像路径（实线蓝色）通常不再是测地线（虚线蓝色）。

这些像路径随后被"提升"到切空间 T f ( X ) N T_{f(X)}\mathcal{N} Tf(X)N 上，形成平滑的弯曲路径（细红色实线）。雅可比矩阵 J \mathbf{J} J 的列向量 j i \mathbf{j}_i ji（粗红线）正是这些提升路径在 f ( X ) f(X) f(X) 处的导数，即
j i = lim ⁡ h → 0 σ i ( h ) h . \mathbf{j}i = \lim{h\to 0} \frac{\sigma_i(h)}{h}. ji=limh→0hσi(h).

每一个 h e i ∈ T X M h e_i \in T_X\mathcal{M} hei∈TXM 都对应一个 j i ∈ T f ( X ) N \mathbf{j}i \in T{f(X)}\mathcal{N} ji∈Tf(X)N，因此最终得到的雅可比矩阵
J = [ j 1 ⋯ j m ] ∈ R n × m \mathbf{J} = [\mathbf{j}_1\ \cdots\ \mathbf{j}m] \in \mathbb{R}^{n\times m} J=[j1 ⋯ jm]∈Rn×m

以线性的方式将向量从
T X M ≃ R m T_X\mathcal{M} \simeq \mathbb{R}^m TXM≃Rm

映射到
T f ( X ) N ≃ R n . T{f(X)}\mathcal{N} \simeq \mathbb{R}^n. Tf(X)N≃Rn.

使用 (41a) 的 Jacobian 计算机制与 (39) 相同，我们一般通过展开分子并提取线性项完成 Jacobian 推导。

例如，对 3D 旋转函数：

f : S O ( 3 ) → R 3 , f ( R ) = R p , f: \mathrm{SO}(3) \rightarrow \mathbb{R}^3, \qquad f(R) = R p, f:SO(3)→R3,f(R)=Rp,

其 Jacobian 为（见附录 B--C5）：

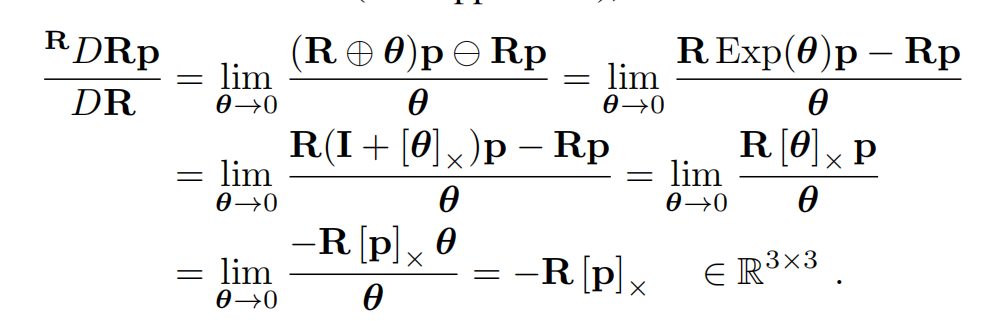
在第 III 节 及附录中可以观察到该机制的诸多示例。需要注意的是，只要函数
f : M → N f:\mathcal{M}\rightarrow\mathcal{N} f:M→N

在不同流形之间进行映射 ，则式 (41a) 中所使用的 加法（plus） 与 减法（minus） 运算符就必须正确选择：

对于定义域流形 M \mathcal{M} M，应使用其对应的 ⊕ \oplus ⊕ 运算；
对于陪域（或像空间）流形 N \mathcal{N} N，则应使用其对应的 ⊖ \ominus ⊖ 运算。

也就是说， ⊕ \oplus ⊕ 与 ⊖ \ominus ⊖ 并非通用的代数运算，而是严格依赖于各自流形结构的局部运算符，这一点在跨流形映射的雅可比推导中尤为关键。

当 τ \tau τ 足够小时，下式成立：

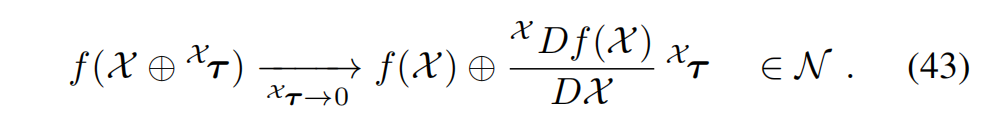
3) 李群上的左 Jacobian（Left Jacobians）

也可以基于左侧的 plus/minus（即 ⊕ , ⊖ \oplus, \ominus ⊕,⊖）来定义导数，得到：

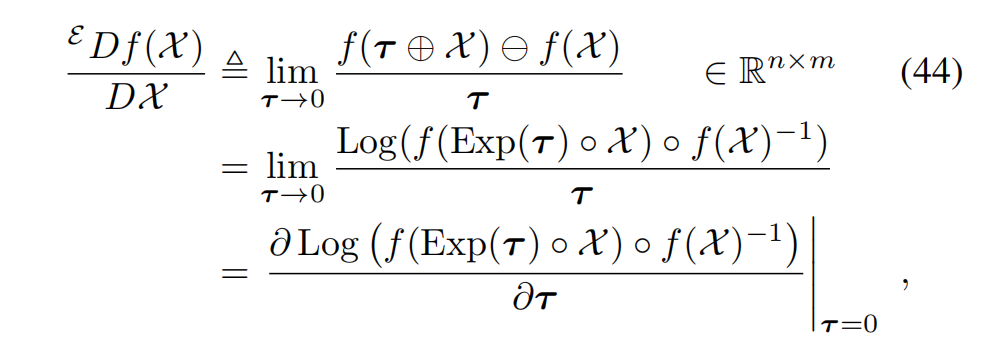
我们称其为 左 Jacobian（left Jacobian）。

注意此时：

τ ∈ T E M \tau \in T_E M τ∈TEM，即在**全局参考系（origin）**的切空间中；
分子属于 T E N T_E N TEN，即 N N N 在全局参考的切空间。

因此左 Jacobian 是一个 n × m n\times m n×m 的矩阵，映射：

T E M → T E N , T_E M \to T_E N, TEM→TEN,

即从 M M M 的李代数映射到 N N N 的李代数（因此标记为 E 上标表示全局参考系）。

对于足够小的 τ \tau τ，有近似式：

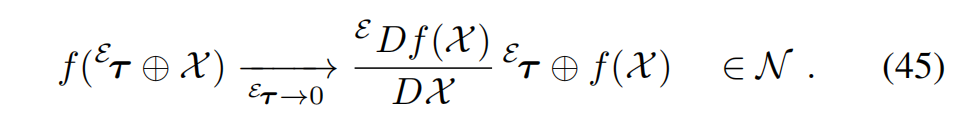
左右 Jacobian 的关系

由式 (32)、(43)、(45) 及图 9 可证明左右 Jacobian 之间满足：

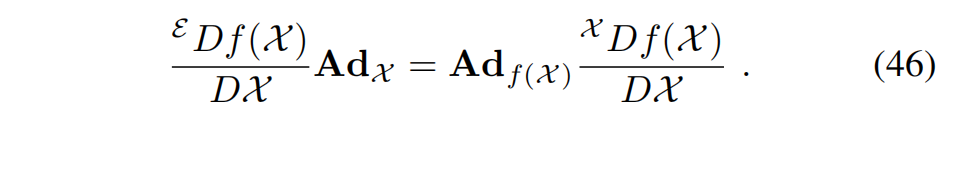
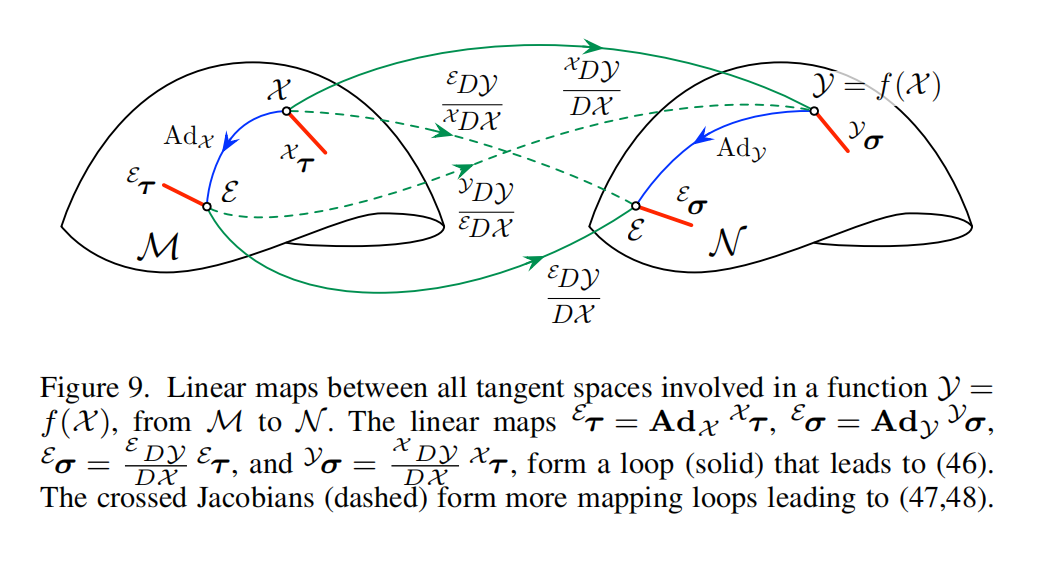
4) 交叉 Jacobian（Crossed right--left Jacobians）

还可以定义使用右加（right-plus）但左减（left-minus）的雅可比，或者反过来使用左加但右减 的形式。尽管这种组合方式并不常见，但在某些情况下仍然是有用的，因为它们能够实现局部切空间与全局切空间之间的映射，或反向映射。

为了简洁起见，这里不对这些雅可比作单独推导，而是通过**伴随算子（adjoint）**将它们与前面定义的雅可比联系起来：

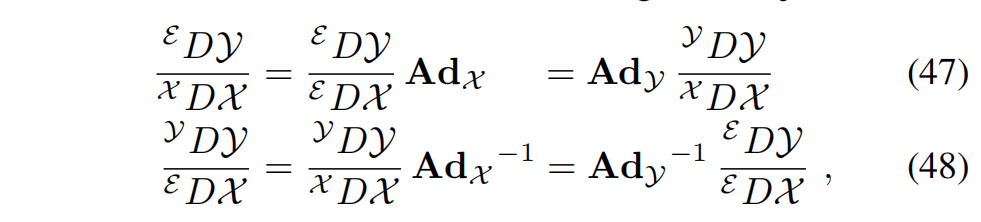
这些关系表明，不同 plus / minus 组合下得到的雅可比矩阵之间，可以通过对应元素处的伴随变换 相互转换。这也再次强调了伴随算子在连接不同参考系与切空间表示中的核心作用。

其中 Y = f ( X ) Y = f(X) Y=f(X)。这里的上下标表示 Jacobian 所表达的参考系（local vs global）。相应的小扰动近似为：

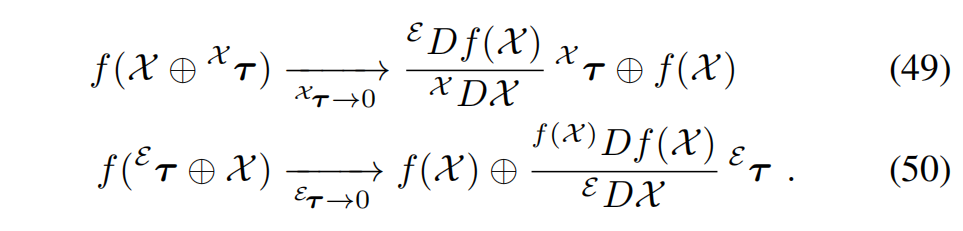
H. 流形上的不确定性与协方差传播

我们在一个点 X ˉ ∈ M \bar{X} \in M Xˉ∈M 的局部切空间 T X ˉ M T_{\bar{X}} M TXˉM 中，使用右加/右减来定义其附近的局部扰动：

X = X ˉ ⊕ τ , τ = X ⊖ X ˉ ∈ T X ˉ M . (51) X = \bar{X} \oplus \tau, \qquad \tau = X \ominus \bar{X} \in T_{\bar{X}} M . \tag{51} X=Xˉ⊕τ,τ=X⊖Xˉ∈TXˉM.(51)

在该切空间定义协方差矩阵（使用期望算子 E [ ⋅ ] E[\cdot] E[⋅]）：

Σ X ≜ E [ τ τ ⊤ ] = E [ ( X ⊖ X ˉ ) ( X ⊖ X ˉ ) ⊤ ] ∈ R m × m , (52) \Sigma_X \triangleq E[\tau \tau^\top]= E[(X\ominus\bar{X})(X\ominus\bar{X})^\top] \in \mathbb{R}^{m\times m}, \tag{52} ΣX≜E[ττ⊤]=E[(X⊖Xˉ)(X⊖Xˉ)⊤]∈Rm×m,(52)

从而使我们能够在流形上定义高斯随机变量 ，
X ∼ N ( X ˉ , Σ X ) , X \sim \mathcal{N}(\bar X,\Sigma_X), X∼N(Xˉ,ΣX),

如图 10 所示。需要注意的是，尽管我们记作 Σ X \Sigma_X ΣX，但该协方差实际上对应的是切空间中的扰动向量 τ \tau τ 的协方差。由于切空间 T M T M TM 的维数 m m m 与流形 M M M 的自由度相一致，因此这样的协方差定义是良好且一致的。

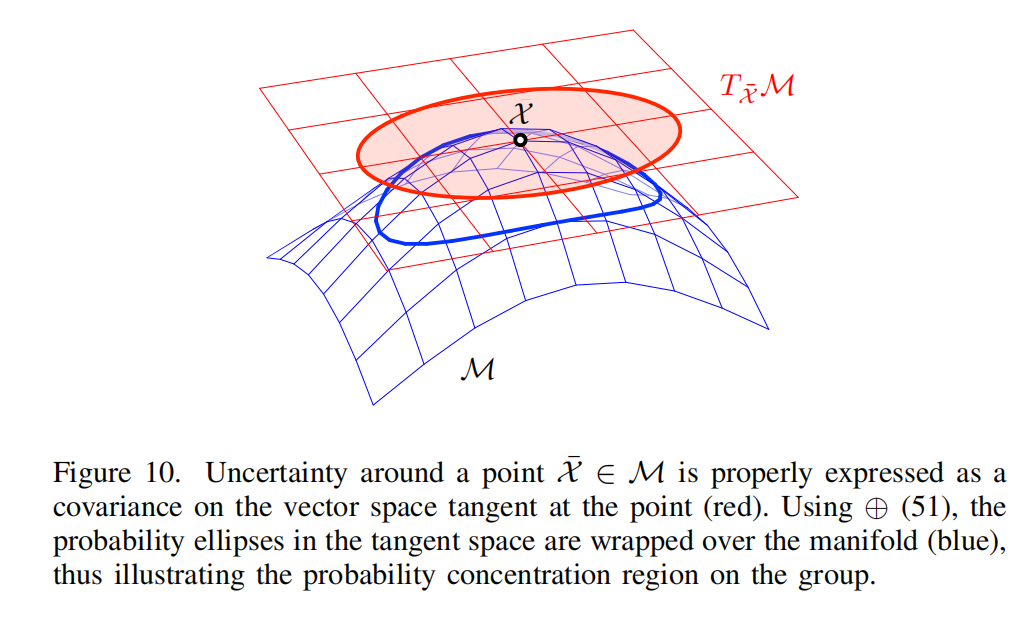
图 10 ：位于点 X ˉ ∈ M \bar{X} \in \mathcal{M} Xˉ∈M 附近的不确定性，应当正确地表示为该点处切向量空间上的协方差 （红色）。通过使用 ⊕ 运算（式 (51)），切空间中的概率椭圆被"包裹"到流形之上（蓝色），从而形象地展示了该李群上的概率集中区域。

在全局参考中的扰动也可以在全局切空间 T E M T_E M TEM 中（使用左加/左减）表示：

X = E τ ⊕ X ˉ , E τ = X ⊖ E X ˉ ∈ T E M . (53) X = {}^{E}\tau \oplus \bar{X}, \qquad {}^{E}\tau = X \ominus_E \bar{X} \in T_E M . \tag{53} X=Eτ⊕Xˉ,Eτ=X⊖EXˉ∈TEM.(53)

这使得我们可以通过式 (52) 中的 left-minus 运算在全局坐标系 下对协方差矩阵进行定义。例如，一个三维姿态如果只在水平面内的旋转 存在不确定性，就可以与如下协方差关联：
E Σ = diag ⁡ ( σ ϕ 2 , σ θ 2 , ∞ ) . {}^{E}\Sigma = \operatorname{diag}(\sigma_\phi^2, \sigma_\theta^2,\infty). EΣ=diag(σϕ2,σθ2,∞).

由于"水平"这一概念是全局性的描述 ，因此协方差 E Σ {}^{E}\Sigma EΣ 必须在全局参考系中给定。

由于全局扰动与局部扰动之间通过伴随变换（式 (30)）相关，它们的协方差可以通过以下方式进行转换：
E Σ X = Ad ⁡ X X Σ X Ad ⁡ X ⊤ . (54) {}^{E}\Sigma_X= \operatorname{Ad}_X {}^{X}\Sigma_X \operatorname{Ad}_X^{\top}. \tag{54} EΣX=AdXXΣXAdX⊤.(54)

对于函数 f : M → N f : M \rightarrow N f:M→N 的协方差传播，其中
X ↦ Y = f ( X ) , X \mapsto Y = f(X), X↦Y=f(X),

只需使用式 (43) 中的线性化以及式 (41a) 给出的雅可比矩阵，便可得到熟悉的协方差传播公式：
Σ Y ≈ D f D X Σ X D f D X ⊤ ∈ R n × n . (55) \Sigma_Y \approx \frac{Df}{DX} \Sigma_X \frac{Df}{DX}^{\top} \in \mathbb{R}^{n \times n}. \tag{55} ΣY≈DXDfΣXDXDf⊤∈Rn×n.(55)

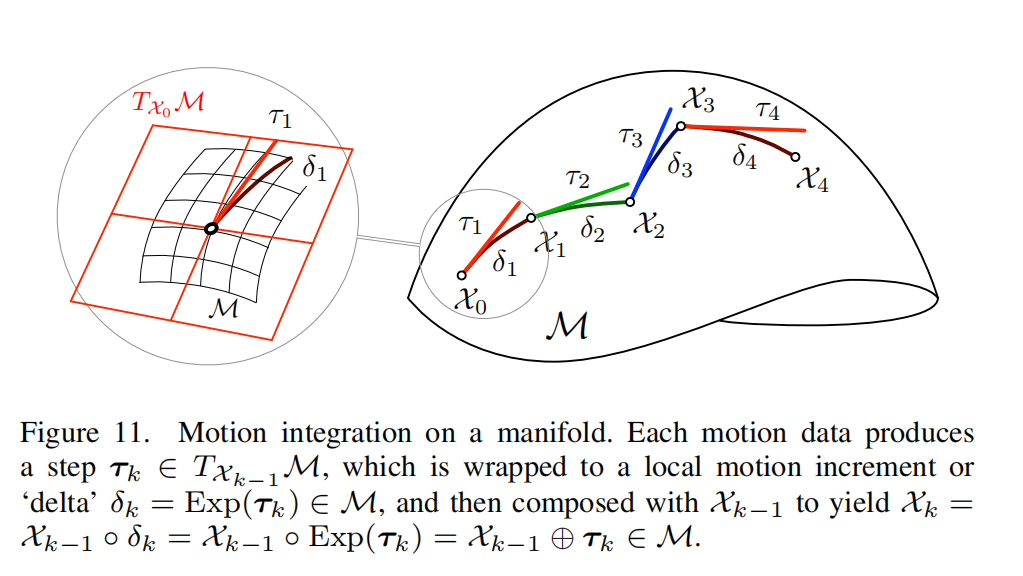
I. 流形上的离散积分

指数映射
X ( t ) = X 0 ∘ Exp ⁡ ( v t ) X(t) = X_0 \circ \operatorname{Exp}(v t) X(t)=X0∘Exp(vt)

实现了将定义在 T X 0 M T_{X_0}\mathcal{M} TX0M 上的常值速度 v v v 进行连续时间积分并映射到流形上 的过程。对于非常值速度 v ( t ) v(t) v(t)，通常的处理方式是将其分段近似为分段常值速度
v k ∈ T X k − 1 M , v_k \in T_{X_{k-1}}\mathcal{M}, vk∈TXk−1M,

每一段持续一个（较短的）时间间隔 δ t k \delta t_k δtk，并写出如下的离散积分形式
X k = X 0 ∘ Exp ⁡ ( v 1 δ t 1 ) ∘ Exp ⁡ ( v 2 δ t 2 ) ∘ ⋯ ∘ Exp ⁡ ( v k δ t k ) = X 0 ⊕ v 1 δ t 1 ⊕ v 2 δ t 2 ⊕ ⋯ ⊕ v k δ t k . \begin{aligned} X_k &= X_0 \circ \operatorname{Exp}(v_1 \delta t_1) \circ \operatorname{Exp}(v_2 \delta t_2) \circ \cdots \circ \operatorname{Exp}(v_k \delta t_k) \\ &= X_0 \oplus v_1 \delta t_1 \oplus v_2 \delta t_2 \oplus \cdots \oplus v_k \delta t_k . \end{aligned} Xk=X0∘Exp(v1δt1)∘Exp(v2δt2)∘⋯∘Exp(vkδtk)=X0⊕v1δt1⊕v2δt2⊕⋯⊕vkδtk.

等价地（见图 11），我们可以定义
τ k = v k δ t k , \tau_k = v_k \delta t_k, τk=vkδtk,

并将该积分过程视为一系列小的离散切向量步长的"累加" ，
τ k ∈ T X k − 1 M , \tau_k \in T_{X_{k-1}}\mathcal{M}, τk∈TXk−1M,

即
X k ≃ X 0 ⊕ τ 1 ⊕ τ 2 ⊕ ⋯ ⊕ τ k . X_k \simeq X_0 \oplus \tau_1 \oplus \tau_2 \oplus \cdots \oplus \tau_k . Xk≃X0⊕τ1⊕τ2⊕⋯⊕τk.

上述所有形式都可以写成如下的递推表达式
X k = X k − 1 ⊕ τ k = X k − 1 ∘ Exp ⁡ ( τ k ) = X k − 1 ∘ Exp ⁡ ( v k δ t k ) . (56) X_k = X_{k-1} \oplus \tau_k = X_{k-1} \circ \operatorname{Exp}(\tau_k) = X_{k-1} \circ \operatorname{Exp}(v_k \delta t_k). \tag{56} Xk=Xk−1⊕τk=Xk−1∘Exp(τk)=Xk−1∘Exp(vkδtk).(56)

常见的例子包括：

将三维角速度 ω \boldsymbol{\omega} ω 积分为旋转矩阵
R k = R k − 1 Exp ⁡ ( ω k δ t ) , R_k = R_{k-1} \operatorname{Exp}(\boldsymbol{\omega}k \delta t), Rk=Rk−1Exp(ωkδt),

或积分为四元数
q k = q k − 1 Exp ⁡ ( ω k δ t ) . q_k = q{k-1} \operatorname{Exp}(\boldsymbol{\omega}_k \delta t). qk=qk−1Exp(ωkδt).