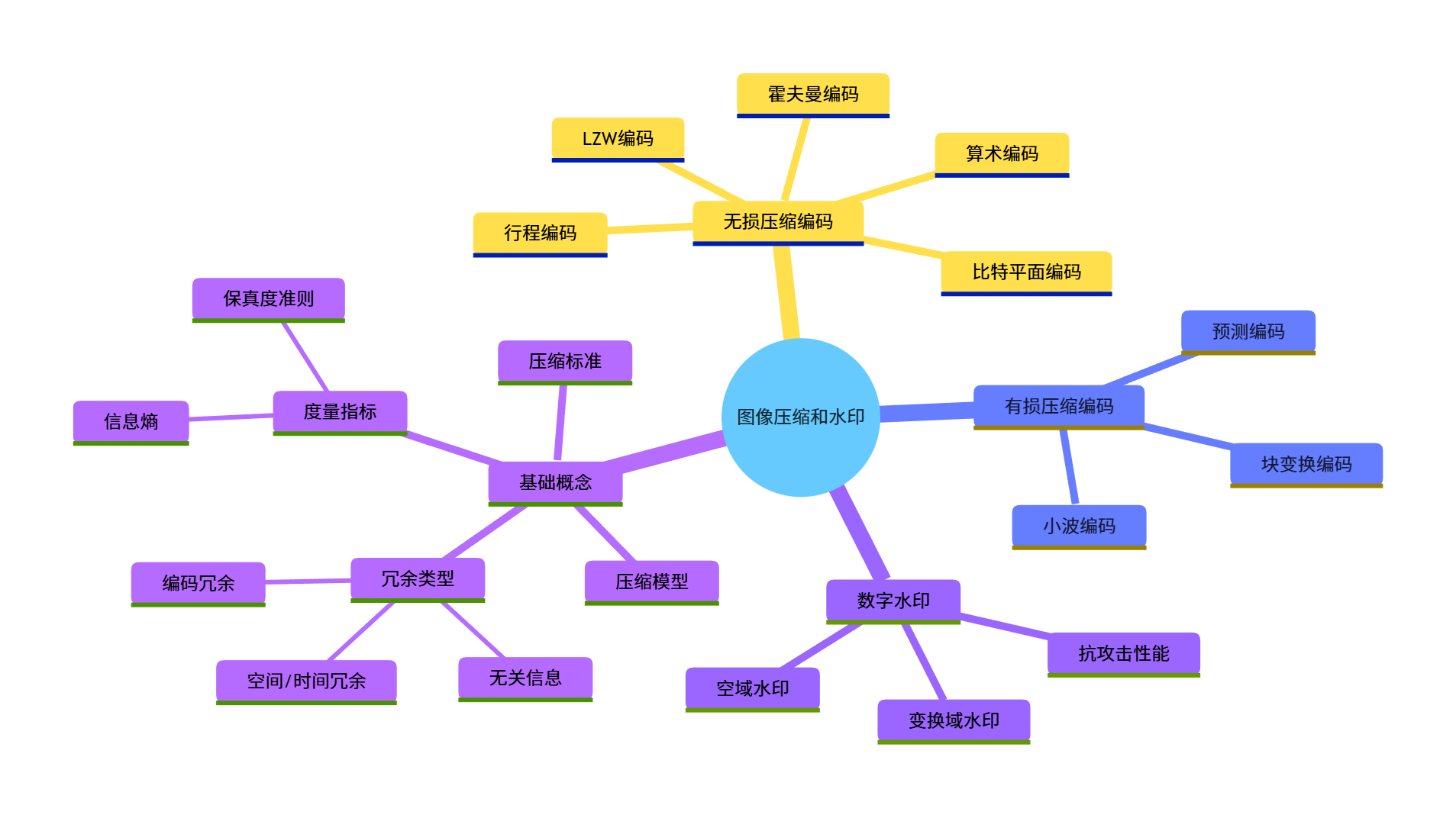
前言
大家好!今天给大家带来《数字图像处理》第 8 章的全面解析 ------ 图像压缩和水印。在这个图像、视频爆炸的时代,图像压缩技术无处不在(比如我们手机里的 JPG 照片、视频网站的流媒体),而数字水印则是多媒体版权保护的核心技术。
本文会从基础概念到实战代码,把图像压缩的各类编码算法(霍夫曼、算术、LZW、小波等)和数字水印技术讲透,每个知识点都配有可直接运行的 Python 代码 、效果对比图,语言通俗易懂,零基础也能看懂!
[本章知识框架(Mermaid 思维导图)](#本章知识框架(Mermaid 思维导图))
[8.1 基础](#8.1 基础)
[8.1.1 编码冗余](#8.1.1 编码冗余)
[8.1.2 空间冗余和时间冗余](#8.1.2 空间冗余和时间冗余)
[8.1.3 无关信息](#8.1.3 无关信息)
[8.1.4 度量图像信息](#8.1.4 度量图像信息)
[1. 信息熵(香农熵)](#1. 信息熵(香农熵))
[2. 平均码字长度](#2. 平均码字长度)
[3. 压缩比](#3. 压缩比)
[8.1.5 保真度准则](#8.1.5 保真度准则)
[1. 客观准则](#1. 客观准则)
[2. 主观准则](#2. 主观准则)
[8.1.6 图像压缩模型](#8.1.6 图像压缩模型)
[8.1.7 图像格式、存储器(容器)和压缩标准](#8.1.7 图像格式、存储器(容器)和压缩标准)
[8.2 霍夫曼编码](#8.2 霍夫曼编码)
[8.3 Golomb 编码](#8.3 Golomb 编码)
[实战代码:Golomb 编码实现](#实战代码:Golomb 编码实现)
[8.4 算术编码](#8.4 算术编码)
[8.4.1 自适应上下文相关概率估计](#8.4.1 自适应上下文相关概率估计)
[8.5 LZW 编码](#8.5 LZW 编码)
[实战代码:LZW 编码实现](#实战代码:LZW 编码实现)
[8.6 行程编码](#8.6 行程编码)
[8.6.1 一维 CCITT 压缩](#8.6.1 一维 CCITT 压缩)
[8.6.2 二维 CCITT 压缩](#8.6.2 二维 CCITT 压缩)
[8.7 基于符号的编码](#8.7 基于符号的编码)
[8.7.1 JBIG2 压缩](#8.7.1 JBIG2 压缩)
[实战代码:JBIG2 简化实现](#实战代码:JBIG2 简化实现)
[8.8 比特平面编码](#8.8 比特平面编码)
[8.9 块变换编码](#8.9 块变换编码)
[8.9.1 变换的选择](#8.9.1 变换的选择)
[8.9.2 子图像尺寸选择](#8.9.2 子图像尺寸选择)
[8.9.3 比特分配](#8.9.3 比特分配)
[实战代码:DCT 块变换编码实现](#实战代码:DCT 块变换编码实现)
[8.10 预测编码](#8.10 预测编码)
[8.10.1 无损预测编码](#8.10.1 无损预测编码)
[8.10.2 运动补偿预测残差](#8.10.2 运动补偿预测残差)
[8.10.3 有损预测编码](#8.10.3 有损预测编码)
[8.10.4 最优预测器](#8.10.4 最优预测器)
[8.10.5 最优化](#8.10.5 最优化)
[8.11 小波编码](#8.11 小波编码)
[8.11.1 小波的选择](#8.11.1 小波的选择)
[8.11.2 分解级数的选择](#8.11.2 分解级数的选择)
[8.11.3 量化器设计](#8.11.3 量化器设计)
[8.11.4 JPEG-2000](#8.11.4 JPEG-2000)
[8.12 数字图像水印](#8.12 数字图像水印)
[实战代码:DWT 域鲁棒水印(JPEG-2000 兼容)](#实战代码:DWT 域鲁棒水印(JPEG-2000 兼容))
引言
图像压缩的核心目标是在尽可能保证图像质量的前提下,减少存储和传输所需的数据量。想象一下:一张未经压缩的 1080P 彩色图像,数据量约为 6MB,而经过 JPEG 压缩后可能只有几十 KB,这就是压缩的价值!
数字水印则是在图像中嵌入不可见的标识信息(比如版权信息),用于版权保护、内容溯源等场景,要求嵌入的水印不影响图像视觉效果,且具有抗攻击(如压缩、裁剪、滤波)能力。
学习目标
- 理解图像冗余的类型和图像信息的度量方法;
- 掌握无损压缩(霍夫曼、LZW、行程编码等)的原理和实现;
- 掌握有损压缩(变换编码、小波编码等)的核心思想和实战;
- 理解数字水印的嵌入和提取原理,能实现基础的水印算法;
- 能根据实际场景选择合适的压缩算法,评估压缩质量。
8.1 基础
8.1.1 编码冗余
核心概念 :编码冗余是指使用了过长的编码来表示图像像素(或符号),比如用 8 位二进制表示一个出现概率极高的灰度值,而理论上可以用更短的编码。
数学表达:

实战代码:计算编码冗余并对比
import numpy as np
import matplotlib.pyplot as plt
from collections import Counter
# 设置中文字体,避免乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 生成模拟图像灰度数据(简化版)
# 模拟高概率灰度值:128(概率0.8),其他灰度值(概率0.2)
np.random.seed(42)
gray_data = np.random.choice([128, 64, 192, 32], size=10000, p=[0.8, 0.05, 0.05, 0.1])
# 1. 计算信息熵
counts = Counter(gray_data)
total = len(gray_data)
entropy = 0
for val, cnt in counts.items():
p = cnt / total
entropy -= p * np.log2(p)
# 2. 计算固定长度编码的平均长度(8位编码)
fixed_len = 8
fixed_avg_len = fixed_len
# 3. 计算编码冗余
coding_redundancy = fixed_avg_len - entropy
# 输出结果
print(f"图像灰度信息熵:{entropy:.2f} 比特/像素")
print(f"8位固定编码平均长度:{fixed_avg_len} 比特/像素")
print(f"编码冗余:{coding_redundancy:.2f} 比特/像素")
# 可视化对比
plt.figure(figsize=(8, 5))
categories = ['信息熵', '8位固定编码', '编码冗余']
values = [entropy, fixed_avg_len, coding_redundancy]
colors = ['#4CAF50', '#FF9800', '#F44336']
bars = plt.bar(categories, values, color=colors)
# 在柱子上标注数值
for bar, val in zip(bars, values):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.1,
f'{val:.2f}', ha='center', fontsize=12)
plt.ylabel('比特/像素')
plt.title('编码冗余对比')
plt.ylim(0, 9)
plt.grid(axis='y', alpha=0.3)
plt.show()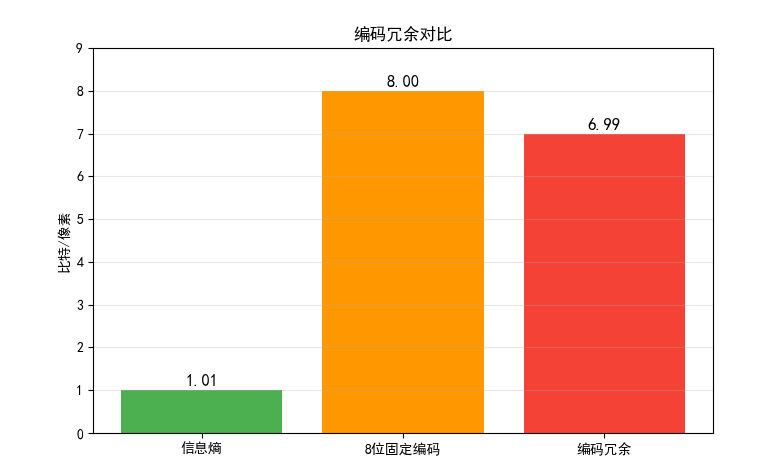
效果对比图位置:运行上述代码后,会生成 "编码冗余对比" 柱状图,直观看到 8 位固定编码的冗余量。
8.1.2 空间冗余和时间冗余
- 空间冗余:图像中相邻像素往往具有相似的灰度值(比如蓝天区域、白色墙壁),这种像素间的相关性就是空间冗余。
- 时间冗余:视频序列中相邻帧的内容高度相似(比如静态场景的视频),这种帧间相关性就是时间冗余。
可视化代码:空间冗余展示
import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 读取测试图像(建议用自己的图像,这里生成模拟图像)
# 生成一个包含大面积相似区域的图像
img = np.ones((256, 256), dtype=np.uint8) * 200 # 背景为浅灰色
# 画一个矩形(深灰色)
img[50:150, 50:150] = 100
# 计算相邻像素的差值(空间相关性)
row_diff = np.abs(img[:, 1:] - img[:, :-1]) # 行方向相邻差值
col_diff = np.abs(img[1:, :] - img[:-1, :]) # 列方向相邻差值
# 统计差值为0的比例(比例越高,空间冗余越大)
row_zero_ratio = (row_diff == 0).sum() / row_diff.size
col_zero_ratio = (col_diff == 0).sum() / col_diff.size
# 可视化
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
# 原始图像
axes[0].imshow(img, cmap='gray', vmin=0, vmax=255)
axes[0].set_title('原始图像(含大面积相似区域)')
axes[0].axis('off')
# 行方向差值
axes[1].imshow(row_diff, cmap='gray', vmin=0, vmax=255)
axes[1].set_title(f'行方向相邻像素差值\n零值比例:{row_zero_ratio:.2f}')
axes[1].axis('off')
# 列方向差值
axes[2].imshow(col_diff, cmap='gray', vmin=0, vmax=255)
axes[2].set_title(f'列方向相邻像素差值\n零值比例:{col_zero_ratio:.2f}')
axes[2].axis('off')
plt.tight_layout()
plt.show()
效果对比图位置:运行后可看到原始图像、行 / 列方向差值图,差值图中大部分区域为黑色(差值为 0),直观体现空间冗余。
8.1.3 无关信息
无关信息是指人类视觉系统无法感知的信息(比如超出人眼分辨能力的细节),压缩时可以去除这些信息而不影响视觉效果(有损压缩的核心思想)。
8.1.4 度量图像信息
- 信息熵(香农熵)

- 平均码字长度

- 压缩比

实战代码:计算图像信息熵和压缩比
import numpy as np
import cv2
import matplotlib.pyplot as plt
from collections import Counter
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 读取图像(用OpenCV,也可以用PIL)
# 替换为自己的图像路径
img = cv2.imread('test_img.jpg', 0) # 0表示灰度图
if img is None:
# 如果读取失败,生成模拟图像
img = np.random.randint(0, 256, size=(256, 256), dtype=np.uint8)
# 1. 计算信息熵
flat_img = img.flatten()
counts = Counter(flat_img)
total = len(flat_img)
entropy = 0
for val, cnt in counts.items():
p = cnt / total
if p > 0:
entropy -= p * np.log2(p)
# 2. 计算压缩前数据量(8位/像素)
original_size = flat_img.size * 8 # 比特
# 3. 模拟霍夫曼编码后的平均长度(简化版,实际需实现霍夫曼编码)
# 这里用熵近似最优编码长度
huffman_avg_len = entropy
compressed_size = flat_img.size * huffman_avg_len
# 4. 计算压缩比
cr = original_size / compressed_size
# 输出结果
print(f"图像信息熵:{entropy:.2f} 比特/像素")
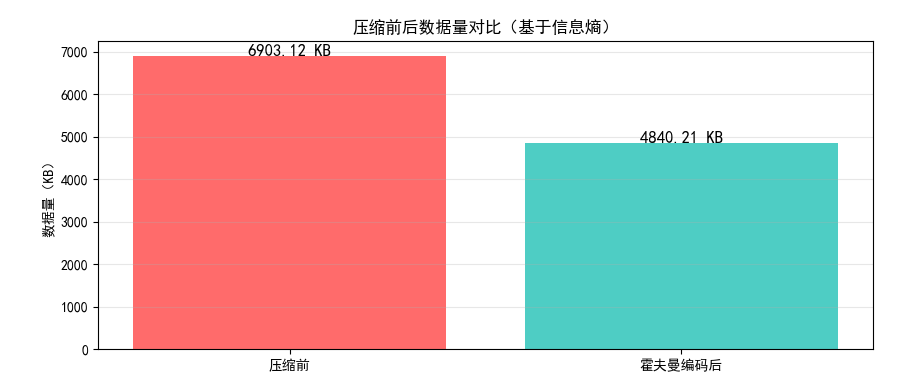
print(f"压缩前数据量:{original_size/1024:.2f} KB")
print(f"霍夫曼编码后数据量:{compressed_size/1024:.2f} KB")
print(f"压缩比:{cr:.2f}")
# 可视化
plt.figure(figsize=(10, 4))
categories = ['压缩前', '霍夫曼编码后']
sizes = [original_size/1024, compressed_size/1024]
colors = ['#FF6B6B', '#4ECDC4']
bars = plt.bar(categories, sizes, color=colors)
for bar, val in zip(bars, sizes):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 1,
f'{val:.2f} KB', ha='center', fontsize=12)
plt.ylabel('数据量(KB)')
plt.title('压缩前后数据量对比(基于信息熵)')
plt.grid(axis='y', alpha=0.3)
plt.show()8.1.5 保真度准则
用于评估压缩后图像的质量,分为客观准则 和主观准则:
- 客观准则

- 主观准则
通过人眼主观评分(如 MOS 评分:1-5 分,5 分为最优)。
实战代码:计算 MSE 和 PSNR
import numpy as np
import cv2
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 读取原始图像和压缩后的图像(这里模拟压缩后的图像)
original_img = cv2.imread('test_img.jpg', 0)
if original_img is None:
original_img = np.random.randint(0, 256, size=(256, 256), dtype=np.uint8)
# 模拟有损压缩后的图像(添加高斯噪声)
np.random.seed(42)
noise = np.random.normal(0, 10, original_img.shape).astype(np.uint8)
compressed_img = np.clip(original_img + noise, 0, 255)
# 计算MSE
mse = np.mean((original_img - compressed_img) ** 2)
# 计算PSNR
if mse == 0:
psnr = float('inf')
else:
psnr = 10 * np.log10((255 ** 2) / mse)
# 输出结果
print(f"均方误差(MSE):{mse:.2f}")
print(f"峰值信噪比(PSNR):{psnr:.2f} dB")
# 可视化对比
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
axes[0].imshow(original_img, cmap='gray', vmin=0, vmax=255)
axes[0].set_title('原始图像')
axes[0].axis('off')
axes[1].imshow(compressed_img, cmap='gray', vmin=0, vmax=255)
axes[1].set_title(f'压缩后图像\nMSE={mse:.2f}, PSNR={psnr:.2f} dB')
axes[1].axis('off')
plt.tight_layout()
plt.show()
效果对比图位置:运行后可看到原始图像和模拟压缩后的图像,以及对应的 MSE/PSNR 值,PSNR 越高(一般 > 30dB),视觉效果越好。
8.1.6 图像压缩模型
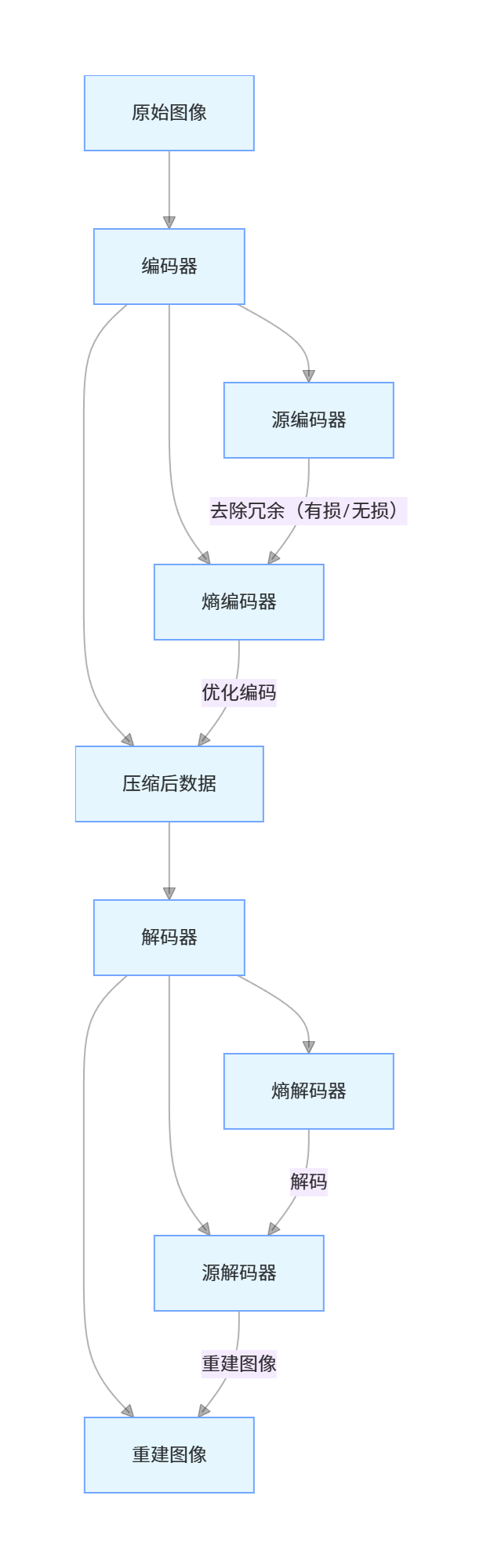
核心说明:
- 源编码器:去除冗余(无损:仅去除编码 / 空间冗余;有损:额外去除无关信息);
- 熵编码器:对源编码器输出的符号进行最优编码,进一步减少编码冗余;
- 解码器是编码器的逆过程。
8.1.7 图像格式、存储器(容器)和压缩标准
| 格式 / 标准 | 类型 | 压缩方式 | 应用场景 |
|---|---|---|---|
| BMP | 位图 | 无损(无压缩) | 无损存储、图像处理 |
| JPEG | 静态图像 | 有损(DCT 变换) | 照片、网页图片 |
| PNG | 静态图像 | 无损(LZW) | 图标、透明图像 |
| GIF | 动态图像 | 无损(LZW) | 简单动图、表情包 |
| JPEG-2000 | 静态图像 | 有损 / 无损(小波变换) | 医疗图像、高清图像 |
| H.264/H.265 | 视频 | 有损(变换 + 预测) | 视频流媒体、监控 |
| JBIG2 | 二值图像 | 无损 / 有损 | 文档扫描、传真 |
8.2 霍夫曼编码
核心原理
霍夫曼编码是一种无损压缩编码 ,核心思想是:对出现概率高的符号分配短编码,概率低的符号分配长编码,且编码是前缀码(无歧义)。
实现步骤
- 统计每个符号的出现概率;
- 构建霍夫曼树(每次选择概率最小的两个节点合并);
- 从根节点遍历到叶子节点,生成每个符号的编码;
- 用生成的编码对图像数据进行编码。
实战代码:霍夫曼编码实现
import numpy as np
import cv2
import heapq
from collections import Counter, defaultdict
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 定义霍夫曼树节点
class HuffmanNode:
def __init__(self, symbol=None, prob=0, left=None, right=None):
self.symbol = symbol
self.prob = prob
self.left = left
self.right = right
# 重载比较运算符,用于堆排序
def __lt__(self, other):
return self.prob < other.prob
# 生成霍夫曼编码表
def build_huffman_code(node, code="", code_dict=None):
if code_dict is None:
code_dict = {}
if node.symbol is not None:
code_dict[node.symbol] = code
else:
build_huffman_code(node.left, code + "0", code_dict)
build_huffman_code(node.right, code + "1", code_dict)
return code_dict
# 霍夫曼编码
def huffman_encoding(data):
# 1. 统计符号概率
counts = Counter(data)
total = len(data)
prob_dict = {sym: cnt/total for sym, cnt in counts.items()}
# 2. 构建霍夫曼堆
heap = [HuffmanNode(symbol=sym, prob=prob) for sym, prob in prob_dict.items()]
heapq.heapify(heap)
# 3. 构建霍夫曼树
while len(heap) > 1:
left = heapq.heappop(heap)
right = heapq.heappop(heap)
merged = HuffmanNode(prob=left.prob + right.prob, left=left, right=right)
heapq.heappush(heap, merged)
# 4. 生成编码表
root = heapq.heappop(heap)
code_dict = build_huffman_code(root)
# 5. 编码数据
encoded_data = "".join([code_dict[sym] for sym in data])
return encoded_data, code_dict, prob_dict
# 霍夫曼解码
def huffman_decoding(encoded_data, code_dict):
# 反转编码表:编码->符号
reverse_code_dict = {code: sym for sym, code in code_dict.items()}
decoded_data = []
current_code = ""
for bit in encoded_data:
current_code += bit
if current_code in reverse_code_dict:
decoded_data.append(reverse_code_dict[current_code])
current_code = ""
return np.array(decoded_data)
# 主函数
if __name__ == "__main__":
# 读取/生成图像数据
img = cv2.imread('test_img.jpg', 0)
if img is None:
img = np.random.randint(0, 256, size=(128, 128), dtype=np.uint8)
flat_img = img.flatten()
# 霍夫曼编码
encoded_data, code_dict, prob_dict = huffman_encoding(flat_img)
# 霍夫曼解码
decoded_flat = huffman_decoding(encoded_data, code_dict)
decoded_img = decoded_flat.reshape(img.shape)
# 计算压缩比
original_size = len(flat_img) * 8 # 8位/像素
compressed_size = len(encoded_data)
cr = original_size / compressed_size
# 计算平均编码长度
avg_len = sum([prob * len(code) for sym, prob in prob_dict.items() for code in [code_dict[sym]]])
# 验证解码是否正确
is_correct = np.array_equal(img, decoded_img)
# 输出结果
print(f"霍夫曼编码平均长度:{avg_len:.2f} 比特/像素")
print(f"压缩前数据量:{original_size/1024:.2f} KB")
print(f"压缩后数据量:{compressed_size/1024:.2f} KB")
print(f"压缩比:{cr:.2f}")
print(f"解码是否正确:{is_correct}")
# 可视化对比
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
axes[0].imshow(img, cmap='gray', vmin=0, vmax=255)
axes[0].set_title('原始图像')
axes[0].axis('off')
axes[1].imshow(decoded_img, cmap='gray', vmin=0, vmax=255)
axes[1].set_title(f'霍夫曼解码后图像\n压缩比={cr:.2f}')
axes[1].axis('off')
plt.tight_layout()
plt.show()
效果对比图位置:运行后可看到原始图像和解码后的图像(完全一致,体现无损压缩),以及压缩比数据。
8.3 Golomb 编码
核心原理

实战代码:Golomb 编码实现
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# Golomb编码
def golomb_encode(x, m):
"""
x: 非负整数
m: 编码参数
"""
if x < 0:
raise ValueError("Golomb编码仅支持非负整数")
# 计算q和r
q = x // m
r = x % m
# 1. 一元编码q:q个1 + 1个0
unary_code = "1" * q + "0"
# 2. 二进制编码r:需要k位,k = ceil(log2(m))
k = int(np.ceil(np.log2(m)))
# 计算2^k - m
rem = (1 << k) - m
# 3. 生成r的编码
if r < rem:
binary_code = bin(r)[2:].zfill(k-1) # k-1位
else:
binary_code = bin(r + rem)[2:].zfill(k) # k位
# 合并编码
return unary_code + binary_code
# Golomb解码
def golomb_decode(code, m):
"""
code: Golomb编码字符串
m: 编码参数
"""
# 1. 解析q(一元编码部分)
q = 0
while q < len(code) and code[q] == "1":
q += 1
# 跳过0
if q >= len(code) or code[q] != "0":
raise ValueError("无效的Golomb编码")
code = code[q+1:]
# 2. 解析r
k = int(np.ceil(np.log2(m)))
rem = (1 << k) - m
if len(code) < k-1:
raise ValueError("无效的Golomb编码")
# 尝试k-1位
r_candidate = int(code[:k-1], 2) if k-1 > 0 else 0
if r_candidate < rem:
r = r_candidate
code = code[k-1:]
else:
if len(code) < k:
raise ValueError("无效的Golomb编码")
r = int(code[:k], 2) - rem
code = code[k:]
# 计算x
x = q * m + r
return x, code
# 主函数
if __name__ == "__main__":
# 测试数据(行程编码的行程长度)
run_lengths = [0, 1, 3, 5, 8, 10, 15, 20]
m = 8 # 编码参数
# 编码
encoded_codes = [golomb_encode(x, m) for x in run_lengths]
# 解码
decoded_lengths = []
for code in encoded_codes:
x, _ = golomb_decode(code, m)
decoded_lengths.append(x)
# 输出结果
print("原始行程长度:", run_lengths)
print("Golomb编码:", encoded_codes)
print("解码后长度:", decoded_lengths)
print("解码是否正确:", run_lengths == decoded_lengths)
# 可视化编码长度对比
original_bits = [np.ceil(np.log2(x+1)) if x > 0 else 1 for x in run_lengths]
encoded_bits = [len(code) for code in encoded_codes]
x = np.arange(len(run_lengths))
width = 0.35
plt.figure(figsize=(10, 6))
plt.bar(x - width/2, original_bits, width, label='固定长度编码', color='#FF6B6B')
plt.bar(x + width/2, encoded_bits, width, label='Golomb编码', color='#4ECDC4')
plt.xlabel('行程长度')
plt.ylabel('编码长度(比特)')
plt.title('Golomb编码 vs 固定长度编码')
plt.xticks(x, run_lengths)
plt.legend()
plt.grid(axis='y', alpha=0.3)
plt.show()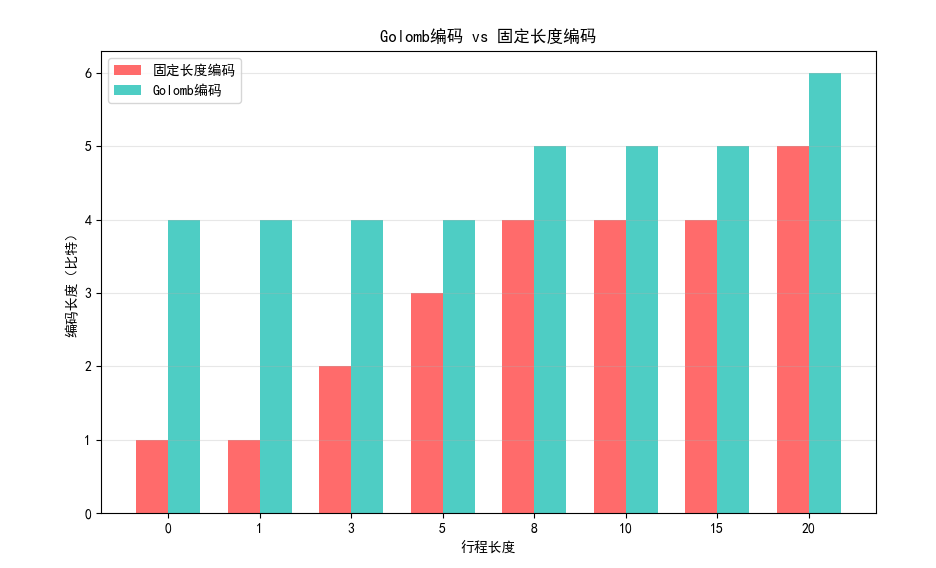
效果对比图位置:运行后可看到 Golomb 编码与固定长度编码的长度对比,Golomb 编码对小数值的行程长度更高效。
8.4 算术编码
核心原理
算术编码不单独为每个符号分配编码,而是将整个符号序列映射到 [0,1) 区间内的一个小数,最终输出该小数的二进制表示。相比霍夫曼编码,算术编码能更接近信息熵,且支持自适应概率估计。
8.4.1 自适应上下文相关概率估计
自适应算术编码会根据已编码的符号动态更新概率分布,无需预先统计符号概率,更适合实时数据压缩。
实战代码:算术编码实现
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 算术编码
def arithmetic_encode(symbols, prob_dict):
"""
symbols: 符号序列
prob_dict: 符号概率字典
"""
# 构建累积概率字典
sorted_syms = sorted(prob_dict.keys())
cum_prob = {}
current = 0
for sym in sorted_syms:
cum_prob[sym] = current
current += prob_dict[sym]
# 初始化区间
low = 0.0
high = 1.0
# 编码每个符号
for sym in symbols:
range_val = high - low
high = low + range_val * (cum_prob[sym] + prob_dict[sym])
low = low + range_val * cum_prob[sym]
# 选择区间中点作为编码值
code = (low + high) / 2
return code, cum_prob
# 算术解码
def arithmetic_decode(code, length, prob_dict, cum_prob):
"""
code: 编码值
length: 符号序列长度
prob_dict: 符号概率字典
cum_prob: 累积概率字典
"""
sorted_syms = sorted(prob_dict.keys())
decoded_syms = []
low = 0.0
high = 1.0
for _ in range(length):
range_val = high - low
# 计算相对位置
pos = (code - low) / range_val
# 找到对应的符号
sym = None
for s in sorted_syms:
if cum_prob[s] <= pos < cum_prob[s] + prob_dict[s]:
sym = s
break
decoded_syms.append(sym)
# 更新区间
high = low + range_val * (cum_prob[sym] + prob_dict[sym])
low = low + range_val * cum_prob[sym]
return decoded_syms
# 自适应算术编码(简化版)
def adaptive_arithmetic_encode(symbols):
# 初始化概率(等概率)
sym_set = list(set(symbols))
prob_dict = {sym: 1/len(sym_set) for sym in sym_set}
codes = []
cum_probs = []
# 逐符号编码,动态更新概率
count_dict = {sym: 1 for sym in sym_set} # 平滑计数,避免概率为0
total = len(sym_set)
low = 0.0
high = 1.0
for sym in symbols:
# 计算当前累积概率
sorted_syms = sorted(count_dict.keys())
cum_prob = {}
current = 0
for s in sorted_syms:
cum_prob[s] = current / total
current += count_dict[s]
# 编码当前符号
range_val = high - low
high = low + range_val * (cum_prob[sym] + count_dict[sym]/total)
low = low + range_val * cum_prob[sym]
# 更新计数和概率
count_dict[sym] += 1
total += 1
codes.append((low + high)/2)
cum_probs.append(cum_prob)
return codes[-1], count_dict
# 主函数
if __name__ == "__main__":
# 测试数据(图像灰度值序列)
symbols = [128, 128, 64, 128, 192, 128, 128, 64, 64, 128]
# 预先统计概率
prob_dict = {128: 0.6, 64: 0.3, 192: 0.1}
# 固定概率算术编码
code, cum_prob = arithmetic_encode(symbols, prob_dict)
decoded_syms = arithmetic_decode(code, len(symbols), prob_dict, cum_prob)
# 自适应算术编码
adaptive_code, final_counts = adaptive_arithmetic_encode(symbols)
# 输出结果
print("原始符号序列:", symbols)
print("固定概率算术编码值:", code)
print("解码后序列:", decoded_syms)
print("自适应算术编码值:", adaptive_code)
print("固定概率解码是否正确:", symbols == decoded_syms)
# 可视化编码效率
# 计算信息熵
entropy = -sum([p * np.log2(p) for p in prob_dict.values()])
# 固定编码长度(8位)
fixed_len = 8 * len(symbols)
# 算术编码长度(二进制位数,用log2(1/(high-low))近似)
range_val = 1.0
for sym in symbols:
range_val *= prob_dict[sym]
arithmetic_bits = np.ceil(-np.log2(range_val))
plt.figure(figsize=(8, 5))
categories = ['8位固定编码', '算术编码', '信息熵下限']
values = [fixed_len, arithmetic_bits, entropy*len(symbols)]
colors = ['#FF9800', '#4CAF50', '#F44336']
bars = plt.bar(categories, values, color=colors)
for bar, val in zip(bars, values):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.5,
f'{val:.1f}', ha='center', fontsize=12)
plt.ylabel('总比特数')
plt.title('算术编码效率对比')
plt.grid(axis='y', alpha=0.3)
plt.show()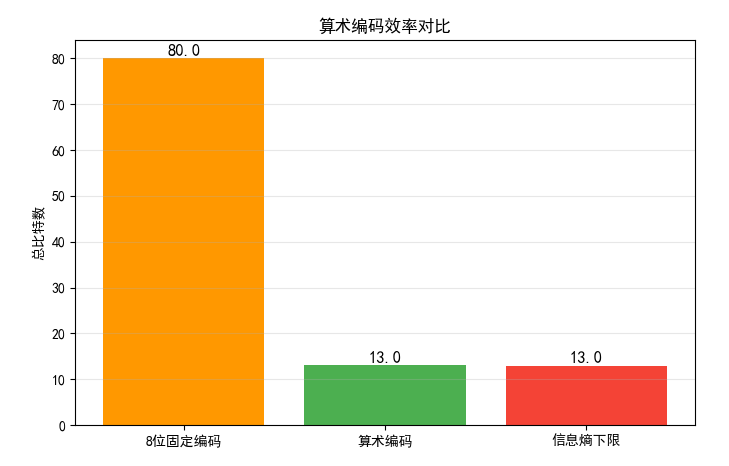
效果对比图位置:运行后可看到算术编码与固定编码、信息熵下限的对比,算术编码更接近信息熵下限,效率更高。
8.5 LZW 编码
核心原理
LZW(Lempel-Ziv-Welch)编码是一种无损压缩算法,核心思想是:
- 初始化字典,包含所有单个符号;
- 遍历数据,逐步构建更长的符号序列,将新序列加入字典;
- 用字典索引代替符号序列,实现压缩。
实战代码:LZW 编码实现
python
import numpy as np
import cv2
import matplotlib.pyplot as plt
# 设置中文字体,避免乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# LZW编码(修复字典键类型,统一为元组)
def lzw_encode(data, max_dict_size=4096):
"""
data: 输入数据(一维数组)
max_dict_size: 字典最大容量
"""
# 1. 初始化字典:单个符号转为长度为1的元组作为键(统一类型)
unique_syms = list(set(data))
# 键:(sym,) 元组,值:索引(避免单个值和元组混用)
dictionary = {(sym,): idx for idx, sym in enumerate(unique_syms)}
next_code = len(unique_syms)
# 2. 编码过程(当前序列统一为元组)
current_seq = (data[0],) # 初始化为元组
encoded = []
for sym in data[1:]:
combined_seq = current_seq + (sym,) # 元组拼接,统一逻辑
if combined_seq in dictionary:
current_seq = combined_seq
else:
# 输出当前序列的索引
encoded.append(dictionary[current_seq])
# 将新序列加入字典(如果字典未满)
if next_code < max_dict_size:
dictionary[combined_seq] = next_code
next_code += 1
# 重置当前序列为单个符号的元组
current_seq = (sym,)
# 输出最后一个序列
encoded.append(dictionary[current_seq])
return encoded, dictionary
# LZW解码(修复类型拼接逻辑)
def lzw_decode(encoded, dictionary):
"""
encoded: 编码后的索引序列
dictionary: 编码时的字典(需要反转)
"""
# 反转字典:索引 -> 符号元组(统一类型)
reverse_dict = {idx: sym_tuple for sym_tuple, idx in dictionary.items()}
decoded = []
# 处理空编码的边界情况
if not encoded:
return np.array([])
# 第一个符号序列
current_code = encoded[0]
current_seq = reverse_dict[current_code]
decoded.extend(current_seq) # 元组直接展开为列表
# 解码剩余符号
for code in encoded[1:]:
# 查找当前编码对应的序列
if code in reverse_dict:
next_seq = reverse_dict[code]
else:
# LZW特殊情况:未在字典中时,用当前序列+当前序列第一个元素
next_seq = current_seq + (current_seq[0],)
# 将序列展开加入解码结果
decoded.extend(next_seq)
# 更新字典(模拟编码时的字典更新逻辑)
new_seq = current_seq + (next_seq[0],)
if len(reverse_dict) < max_dict_size and new_seq not in dictionary:
dictionary[new_seq] = len(dictionary)
reverse_dict[len(reverse_dict)] = new_seq
# 更新当前序列为下一个序列
current_seq = next_seq
# 转换为numpy数组(与原始数据类型一致)
return np.array(decoded, dtype=np.uint8)
# 主函数
if __name__ == "__main__":
# 配置参数
max_dict_size = 4096 # LZW字典最大容量(2^12)
img_path = '../picture/Java.png' # 替换为你的图像路径
# 读取/生成图像数据
img = cv2.imread(img_path, 0) # 0表示灰度图
if img is None:
print(f"警告:未找到图像 {img_path},使用随机生成图像测试")
np.random.seed(42) # 固定随机种子,便于复现
img = np.random.randint(0, 256, size=(128, 128), dtype=np.uint8)
flat_img = img.flatten() # 展平为一维数组
print(f"图像尺寸:{img.shape},展平后长度:{len(flat_img)}")
# LZW编码
encoded, dict_ = lzw_encode(flat_img, max_dict_size)
# LZW解码
decoded_flat = lzw_decode(encoded, dict_.copy()) # 传字典副本,避免原字典被修改
# 截断到原始长度(防止解码长度略长的情况)
decoded_flat = decoded_flat[:len(flat_img)]
decoded_img = decoded_flat.reshape(img.shape)
# 计算压缩比
original_size = len(flat_img) * 8 # 原始数据量(8位/像素,单位:比特)
compressed_size = len(encoded) * 12 # 编码后每个索引用12位(4096=2^12)
cr = original_size / compressed_size # 压缩比
# 验证解码是否正确
is_correct = np.array_equal(img.flatten(), decoded_flat)
# 输出结果
print("=" * 50)
print(f"原始数据长度:{len(flat_img)} 像素")
print(f"编码后索引数量:{len(encoded)}")
print(f"压缩前数据量:{original_size / 1024:.2f} KB")
print(f"压缩后数据量:{compressed_size / 1024:.2f} KB")
print(f"压缩比:{cr:.2f}")
print(f"解码是否完全正确:{is_correct}")
print("=" * 50)
# 可视化对比
fig, axes = plt.subplots(1, 2, figsize=(12, 10))
# 原始图像
axes[0].imshow(img, cmap='gray', vmin=0, vmax=255)
axes[0].set_title('原始图像', fontsize=14)
axes[0].axis('off')
# 解码后图像
axes[1].imshow(decoded_img, cmap='gray', vmin=0, vmax=255)
axes[1].set_title(f'LZW解码后图像\n压缩比={cr:.2f}', fontsize=14)
axes[1].axis('off')
plt.tight_layout()
plt.show()
效果对比图位置:运行后可看到原始图像和 LZW 解码后的图像(无损),以及压缩比数据(LZW 对重复序列多的图像压缩效果更好)。
8.6 行程编码
核心原理
行程编码(RLE)适用于连续重复的符号序列,用 "符号 + 重复次数" 代替连续的符号,比如 "AAAAA" 编码为 "A5"。
8.6.1 一维 CCITT 压缩
一维 CCITT 压缩是针对二值图像的行程编码标准,仅对每行的黑像素行程长度进行编码。
8.6.2 二维 CCITT 压缩
二维 CCITT 压缩利用前一行的信息预测当前行的行程长度,进一步提高压缩效率。
实战代码:行程编码实现
import numpy as np
import cv2
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 一维行程编码
def rle_encode_1d(data):
"""
一维行程编码
data: 一维数组
"""
if len(data) == 0:
return []
encoded = []
current_sym = data[0]
count = 1
for sym in data[1:]:
if sym == current_sym:
count += 1
else:
encoded.append((current_sym, count))
current_sym = sym
count = 1
# 加入最后一个序列
encoded.append((current_sym, count))
return encoded
# 一维行程解码
def rle_decode_1d(encoded):
"""
一维行程解码
encoded: 编码后的列表,元素为(符号, 次数)
"""
decoded = []
for sym, count in encoded:
decoded.extend([sym]*count)
return np.array(decoded)
# 二维CCITT压缩(简化版)
def rle_encode_2d(img):
"""
二维行程编码(针对二值图像)
img: 二值图像(0/255)
"""
encoded = []
# 第一行用一维编码
first_row = img[0]
encoded.append(rle_encode_1d(first_row))
# 后续行利用前一行信息(简化版:仅编码与前一行不同的区域)
for i in range(1, img.shape[0]):
current_row = img[i]
prev_row = img[i-1]
# 找到与前一行不同的位置
diff_mask = current_row != prev_row
if np.any(diff_mask):
# 对不同区域进行一维编码
encoded.append(rle_encode_1d(current_row[diff_mask]))
else:
# 与前一行相同,标记为0
encoded.append([(0, 0)])
return encoded
# 主函数
if __name__ == "__main__":
# 生成二值图像(适合行程编码)
img = np.zeros((256, 256), dtype=np.uint8)
# 生成连续的白色区域
img[50:100, :] = 255
img[100:150, 50:200] = 255
img[150:200, :] = 255
# 一维行程编码
flat_img = img.flatten()
encoded_1d = rle_encode_1d(flat_img)
decoded_1d = rle_decode_1d(encoded_1d)
decoded_img_1d = decoded_1d.reshape(img.shape)
# 二维行程编码
encoded_2d = rle_encode_2d(img)
# 计算压缩比
original_size = len(flat_img) * 8
# 一维编码:每个(符号,次数)对用16位(8位符号+8位次数)
encoded_1d_size = len(encoded_1d) * 16
# 二维编码:简化计算
encoded_2d_size = sum([len(row) * 16 for row in encoded_2d])
cr_1d = original_size / encoded_1d_size
cr_2d = original_size / encoded_2d_size
# 输出结果
print(f"原始数据量:{original_size/1024:.2f} KB")
print(f"一维RLE编码数据量:{encoded_1d_size/1024:.2f} KB,压缩比:{cr_1d:.2f}")
print(f"二维RLE编码数据量:{encoded_2d_size/1024:.2f} KB,压缩比:{cr_2d:.2f}")
print(f"一维RLE解码是否正确:{np.array_equal(img, decoded_img_1d)}")
# 可视化对比
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
axes[0].imshow(img, cmap='gray', vmin=0, vmax=255)
axes[0].set_title('原始二值图像')
axes[0].axis('off')
axes[1].imshow(decoded_img_1d, cmap='gray', vmin=0, vmax=255)
axes[1].set_title(f'一维RLE解码后图像\n压缩比={cr_1d:.2f}')
axes[1].axis('off')
plt.tight_layout()
plt.show()
# 可视化压缩比对比
plt.figure(figsize=(8, 5))
categories = ['一维RLE', '二维RLE']
cr_vals = [cr_1d, cr_2d]
colors = ['#FF6B6B', '#4ECDC4']
bars = plt.bar(categories, cr_vals, color=colors)
for bar, val in zip(bars, cr_vals):
plt.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.1,
f'{val:.2f}', ha='center', fontsize=12)
plt.ylabel('压缩比')
plt.title('一维vs二维行程编码压缩比')
plt.grid(axis='y', alpha=0.3)
plt.show()
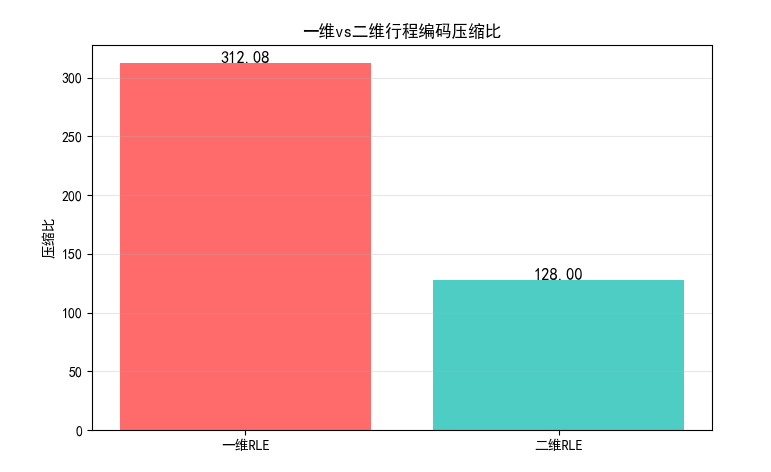
效果对比图位置:
- 原始二值图像与一维 RLE 解码后的图像对比;
- 一维 / 二维 RLE 压缩比对比图,二维压缩比更高。
8.7 基于符号的编码
8.7.1 JBIG2 压缩
JBIG2 是针对二值图像的压缩标准,核心是:
- 对图像中的字符 / 符号进行模板匹配;
- 用模板索引代替重复的符号,大幅提高压缩效率(比如文档扫描件)。
实战代码:JBIG2 简化实现
import numpy as np
import cv2
import matplotlib.pyplot as plt
from skimage.feature import match_template
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# JBIG2简化实现(符号匹配)
def jbig2_simplified_encode(img, template_size=(16, 16)):
"""
简化版JBIG2编码
img: 二值图像
template_size: 符号模板尺寸
"""
h, w = img.shape
th, tw = template_size
# 1. 提取符号模板
templates = []
template_pos = []
# 滑动窗口提取模板
for y in range(0, h - th + 1, th):
for x in range(0, w - tw + 1, tw):
template = img[y:y+th, x:x+tw]
# 跳过全0模板
if np.sum(template) > 0:
# 检查是否已存在相似模板
match_found = False
for idx, t in enumerate(templates):
if np.array_equal(t, template):
template_pos.append((idx, x, y))
match_found = True
break
if not match_found:
templates.append(template)
template_pos.append((len(templates)-1, x, y))
# 2. 编码数据:模板库 + 位置索引
encoded = {
'templates': templates,
'positions': template_pos
}
return encoded
# JBIG2简化解码
def jbig2_simplified_decode(encoded, img_shape, template_size=(16, 16)):
"""
简化版JBIG2解码
"""
h, w = img_shape
th, tw = template_size
decoded = np.zeros(img_shape, dtype=np.uint8)
templates = encoded['templates']
positions = encoded['positions']
for idx, x, y in positions:
decoded[y:y+th, x:x+tw] = templates[idx]
return decoded
# 主函数
if __name__ == "__main__":
# 读取/生成文档类二值图像
# 建议用包含重复字符的文档图像,这里生成模拟图像
img = np.zeros((128, 256), dtype=np.uint8)
# 生成重复的"符号"(矩形)
for i in range(4):
for j in range(8):
img[16*i+2:16*i+14, 16*j+2:16*j+14] = 255
# JBIG2编码
encoded = jbig2_simplified_encode(img)
# JBIG2解码
decoded_img = jbig2_simplified_decode(encoded, img.shape)
# 计算压缩比
original_size = img.size * 8
# 编码后:模板库大小 + 位置索引大小
template_size = sum([t.size * 8 for t in encoded['templates']])
position_size = len(encoded['positions']) * 16 # 每个位置用16位
encoded_size = template_size + position_size
cr = original_size / encoded_size
# 输出结果
print(f"模板数量:{len(encoded['templates'])}")
print(f"位置索引数量:{len(encoded['positions'])}")
print(f"原始数据量:{original_size/1024:.2f} KB")
print(f"JBIG2编码数据量:{encoded_size/1024:.2f} KB")
print(f"压缩比:{cr:.2f}")
# 可视化对比
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
axes[0].imshow(img, cmap='gray', vmin=0, vmax=255)
axes[0].set_title('原始文档图像')
axes[0].axis('off')
axes[1].imshow(decoded_img, cmap='gray', vmin=0, vmax=255)
axes[1].set_title(f'JBIG2解码后图像\n压缩比={cr:.2f}')
axes[1].axis('off')
plt.tight_layout()
plt.show()
# 可视化模板库
if encoded['templates']:
fig, axes = plt.subplots(1, len(encoded['templates']), figsize=(10, 2))
if len(encoded['templates']) == 1:
axes = [axes]
for idx, (ax, template) in enumerate(zip(axes, encoded['templates'])):
ax.imshow(template, cmap='gray', vmin=0, vmax=255)
ax.set_title(f'模板{idx}')
ax.axis('off')
plt.tight_layout()
plt.show()

效果对比图位置:
- 原始文档图像与 JBIG2 解码后的图像对比;
- JBIG2 模板库可视化,可看到重复符号被合并为少量模板。
8.8 比特平面编码
核心原理
比特平面编码将图像的每个像素的二进制位分解为多个比特平面(如 8 位图像分为 8 个比特平面),对每个比特平面单独编码(通常用行程编码)。
实战代码:比特平面编码实现
python
import numpy as np
import cv2
import matplotlib.pyplot as plt
# 设置中文字体,避免乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 一维行程编码(RLE):适用于比特平面的0/255序列
def rle_encode_1d(data):
"""
对一维数组进行行程编码
:param data: 一维数组(元素为0或255)
:return: 编码后的列表,格式为[(值, 长度), ...]
"""
if len(data) == 0:
return []
encoded = []
current_val = data[0]
count = 1
for val in data[1:]:
if val == current_val:
count += 1
else:
encoded.append((current_val, count))
current_val = val
count = 1
# 添加最后一个行程
encoded.append((current_val, count))
return encoded
# 一维行程解码(RLE)
def rle_decode_1d(encoded):
"""
对行程编码结果进行解码
:param encoded: 编码后的列表,格式为[(值, 长度), ...]
:return: 解码后的一维数组
"""
decoded = []
for val, count in encoded:
decoded.extend([val] * count)
return np.array(decoded, dtype=np.uint8)
# 分解比特平面
def decompose_bit_planes(img):
"""
将8位灰度图像分解为8个比特平面
:param img: 8位灰度图像(uint8)
:return: 8个比特平面(0/255)
"""
bit_planes = []
for i in range(8):
# 提取第i位(0=最低位,7=最高位)
bit_plane = (img >> i) & 1 # 得到0/1矩阵
bit_plane = bit_plane * 255 # 转换为0/255便于显示和编码
bit_planes.append(bit_plane.astype(np.uint8))
return bit_planes
# 重构图像
def reconstruct_from_bit_planes(bit_planes):
"""
从8个比特平面重构原始灰度图像
:param bit_planes: 8个比特平面(0/255)
:return: 重构的灰度图像
"""
img = np.zeros_like(bit_planes[0], dtype=np.uint8)
for i in range(8):
# 将比特平面转换为0/1
bp = (bit_planes[i] > 0).astype(np.uint8)
# 恢复对应位的权重
img += bp << i
return img
# 比特平面编码(结合行程编码)
def bit_plane_encode(bit_planes):
"""
对每个比特平面进行行程编码
:param bit_planes: 8个比特平面
:return: 编码后的比特平面列表
"""
encoded_planes = []
for bp in bit_planes:
flat_bp = bp.flatten() # 展平为一维数组
encoded = rle_encode_1d(flat_bp)
encoded_planes.append(encoded)
return encoded_planes
# 比特平面解码
def bit_plane_decode(encoded_planes, img_shape):
"""
解码比特平面
:param encoded_planes: 编码后的比特平面列表
:param img_shape: 原始图像形状
:return: 解码后的8个比特平面
"""
bit_planes = []
for encoded in encoded_planes:
decoded_flat = rle_decode_1d(encoded)
decoded_bp = decoded_flat.reshape(img_shape) # 恢复二维形状
bit_planes.append(decoded_bp)
return bit_planes
# 主函数
if __name__ == "__main__":
# 读取图像(替换为你的图像路径)
img_path = '../picture/CSGO.jpg'
img = cv2.imread(img_path, 0) # 0表示灰度图
# 若图像读取失败,生成随机图像
if img is None:
print(f"警告:未找到图像 {img_path},使用随机生成图像测试")
np.random.seed(42) # 固定随机种子,便于复现
img = np.random.randint(0, 256, size=(256, 256), dtype=np.uint8)
# 分解比特平面
bit_planes = decompose_bit_planes(img)
# 比特平面编码
encoded_planes = bit_plane_encode(bit_planes)
# 比特平面解码
decoded_planes = bit_plane_decode(encoded_planes, img.shape)
# 重构图像
reconstructed_img = reconstruct_from_bit_planes(decoded_planes)
# 计算压缩比
original_size = img.size * 8 # 原始数据量(8位/像素,单位:比特)
# 编码后数据量:每个RLE对存储(值1位 + 长度15位)≈16位/对
encoded_size = sum([len(enc) * 16 for enc in encoded_planes])
cr = original_size / encoded_size # 压缩比
# 输出结果
print("=" * 60)
print(f"图像尺寸:{img.shape}")
print(f"原始数据量:{original_size / 1024:.2f} KB")
print(f"比特平面编码数据量:{encoded_size / 1024:.2f} KB")
print(f"压缩比:{cr:.2f}")
print(f"重构是否完全正确:{np.array_equal(img, reconstructed_img)}")
print("=" * 60)
# 可视化8个比特平面
fig, axes = plt.subplots(2, 4, figsize=(16, 16))
axes = axes.flatten()
for i in range(8):
axes[i].imshow(bit_planes[i], cmap='gray', vmin=0, vmax=255)
axes[i].set_title(f'比特平面 {i}({"最高位" if i == 7 else "最低位" if i == 0 else ""})', fontsize=12)
axes[i].axis('off')
plt.suptitle('图像的8个比特平面分解', fontsize=16)
plt.tight_layout()
plt.show()
# 可视化原始图像和重构图像
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
# 原始图像
axes[0].imshow(img, cmap='gray', vmin=0, vmax=255)
axes[0].set_title('原始图像', fontsize=14)
axes[0].axis('off')
# 重构图像
axes[1].imshow(reconstructed_img, cmap='gray', vmin=0, vmax=255)
axes[1].set_title(f'比特平面重构图像\n压缩比={cr:.2f}', fontsize=14)
axes[1].axis('off')
plt.tight_layout()
plt.show()

效果对比图位置:
- 8 个比特平面的可视化(高位平面保留图像主要信息,低位平面是细节 / 噪声);
- 原始图像与比特平面重构图像对比。
8.9 块变换编码
核心原理
块变换编码是有损压缩的核心,步骤:
- 将图像分为若干子块(如 8x8);
- 对每个子块进行正交变换(如 DCT);
- 对变换系数进行量化(去除小系数,有损核心);
- 对量化后的系数编码(如行程编码 + 霍夫曼编码)。
8.9.1 变换的选择
常用变换:
- DCT(离散余弦变换):能量集中性好,JPEG 采用;
- DFT(离散傅里叶变换):有复数运算,较少用;
- KLT(卡拉曼滤波变换):最优,但计算复杂。
8.9.2 子图像尺寸选择
- 太小(如 4x4):变换增益低;
- 太大(如 16x16):块效应明显;
- JPEG 采用 8x8 子块。
8.9.3 比特分配
对重要的变换系数(如 DC 系数、低频 AC 系数)分配更多比特,次要系数分配更少比特。
实战代码:DCT 块变换编码实现
import numpy as np
import cv2
import matplotlib.pyplot as plt
from scipy.fftpack import dct, idct
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 8x8 DCT变换
def dct_2d(block):
"""
2D DCT变换
"""
return dct(dct(block.T, norm='ortho').T, norm='ortho')
# 8x8 IDCT变换
def idct_2d(block):
"""
2D IDCT逆变换
"""
return idct(idct(block.T, norm='ortho').T, norm='ortho')
# JPEG量化矩阵(亮度)
JPEG_QUANT_MAT = np.array([
[16, 11, 10, 16, 24, 40, 51, 61],
[12, 12, 14, 19, 26, 58, 60, 55],
[14, 13, 16, 24, 40, 57, 69, 56],
[14, 17, 22, 29, 51, 87, 80, 62],
[18, 22, 37, 56, 68, 109, 103, 77],
[24, 35, 55, 64, 81, 104, 113, 92],
[49, 64, 78, 87, 103, 121, 120, 101],
[72, 92, 95, 98, 112, 100, 103, 99]
])
# 块变换编码
def block_transform_encode(img, block_size=8, quant_mat=JPEG_QUANT_MAT):
"""
块DCT变换编码
"""
h, w = img.shape
# 填充图像到块大小的整数倍
pad_h = (block_size - h % block_size) % block_size
pad_w = (block_size - w % block_size) % block_size
img_padded = np.pad(img, ((0, pad_h), (0, pad_w)), mode='constant')
encoded = []
h_padded, w_padded = img_padded.shape
# 分块处理
for y in range(0, h_padded, block_size):
for x in range(0, w_padded, block_size):
block = img_padded[y:y+block_size, x:x+block_size]
# 转换为0-255 -> -128-127
block = block - 128
# DCT变换
dct_block = dct_2d(block)
# 量化
quant_block = np.round(dct_block / quant_mat)
encoded.append(quant_block)
return encoded, (pad_h, pad_w)
# 块变换解码
def block_transform_decode(encoded, pad_size, img_shape, block_size=8, quant_mat=JPEG_QUANT_MAT):
"""
块IDCT逆变换解码
"""
pad_h, pad_w = pad_size
h, w = img_shape
h_padded = h + pad_h
w_padded = w + pad_w
img_recon = np.zeros((h_padded, w_padded), dtype=np.float32)
idx = 0
# 分块解码
for y in range(0, h_padded, block_size):
for x in range(0, w_padded, block_size):
quant_block = encoded[idx]
idx += 1
# 反量化
dct_block = quant_block * quant_mat
# IDCT逆变换
block = idct_2d(dct_block)
# 转换回0-255
block = block + 128
# 裁剪到0-255
block = np.clip(block, 0, 255)
img_recon[y:y+block_size, x:x+block_size] = block
# 去除填充
img_recon = img_recon[:h, :w].astype(np.uint8)
return img_recon
# 主函数
if __name__ == "__main__":
# 读取图像
img = cv2.imread('test_img.jpg', 0)
if img is None:
img = np.random.randint(0, 256, size=(256, 256), dtype=np.uint8)
# 块变换编码
encoded, pad_size = block_transform_encode(img)
# 块变换解码
recon_img = block_transform_decode(encoded, pad_size, img.shape)
# 计算PSNR
mse = np.mean((img - recon_img) ** 2)
psnr = 10 * np.log10((255**2)/mse) if mse > 0 else float('inf')
# 输出结果
print(f"重建图像PSNR:{psnr:.2f} dB")
# 可视化对比
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
axes[0].imshow(img, cmap='gray', vmin=0, vmax=255)
axes[0].set_title('原始图像')
axes[0].axis('off')
axes[1].imshow(recon_img, cmap='gray', vmin=0, vmax=255)
axes[1].set_title(f'DCT块变换重建图像\nPSNR={psnr:.2f} dB')
axes[1].axis('off')
plt.tight_layout()
plt.show()
# 可视化单个8x8块的DCT变换
# 提取第一个块
y, x = 0, 0
block = img[y:y+8, x:x+8]
dct_block = dct_2d(block - 128)
quant_block = np.round(dct_block / JPEG_QUANT_MAT)
idct_block = idct_2d(quant_block * JPEG_QUANT_MAT) + 128
fig, axes = plt.subplots(2, 2, figsize=(10, 10))
axes[0,0].imshow(block, cmap='gray', vmin=0, vmax=255)
axes[0,0].set_title('原始8x8块')
axes[0,0].axis('off')
axes[0,1].imshow(dct_block, cmap='gray', vmin=-np.max(np.abs(dct_block)), vmax=np.max(np.abs(dct_block)))
axes[0,1].set_title('DCT变换系数')
axes[0,1].axis('off')
axes[1,0].imshow(quant_block, cmap='gray', vmin=-np.max(np.abs(quant_block)), vmax=np.max(np.abs(quant_block)))
axes[1,0].set_title('量化后系数')
axes[1,0].axis('off')
axes[1,1].imshow(idct_block, cmap='gray', vmin=0, vmax=255)
axes[1,1].set_title('IDCT重建块')
axes[1,1].axis('off')
plt.tight_layout()
plt.show()

效果对比图位置:
- 原始图像与 DCT 块变换重建图像对比(可看到轻微块效应,PSNR 越高效果越好);
- 单个 8x8 块的 DCT 变换 / 量化 / 重建过程可视化。
8.10 预测编码
预测编码的核心是利用图像像素的空间 / 时间相关性,用已编码像素预测当前像素,仅编码预测误差,分为无损和有损两类,是视频压缩(如 H.264)的核心技术之一。
8.10.1 无损预测编码
核心原理:无损预测编码(如 DPCM,差分脉冲编码调制)通过线性预测器计算当前像素的预测值,编码 "实际值 - 预测值" 的残差,残差无量化,因此可完全重建原始图像。
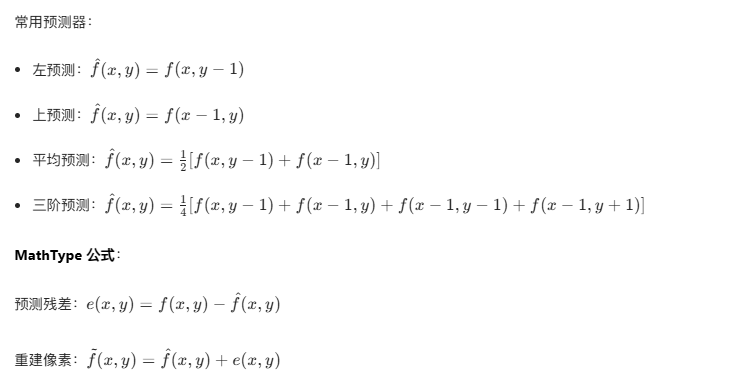
实战代码:无损 DPCM 预测编码
import numpy as np
import cv2
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def dpcm_encode_lossless(img, predictor_type='avg'):
"""
无损DPCM编码
:param img: 输入灰度图像
:param predictor_type: 预测器类型:left/top/avg/3rd
:return: 残差矩阵、重建图像
"""
h, w = img.shape
img = img.astype(np.int16) # 避免溢出
residual = np.zeros_like(img) # 残差矩阵
recon = np.zeros_like(img) # 重建图像
# 初始化:第一行、第一列直接复制
recon[0, :] = img[0, :]
recon[:, 0] = img[:, 0]
residual[0, :] = img[0, :] # 无预测,残差=原值
residual[:, 0] = img[:, 0]
# 逐像素预测编码
for y in range(1, h):
for x in range(1, w):
# 计算预测值
if predictor_type == 'left':
pred = recon[y, x-1]
elif predictor_type == 'top':
pred = recon[y-1, x]
elif predictor_type == 'avg':
pred = (recon[y, x-1] + recon[y-1, x]) // 2
elif predictor_type == '3rd':
# 三阶预测:左+上+左上的平均(简化版)
pred = (recon[y, x-1] + recon[y-1, x] + recon[y-1, x-1]) // 3
else:
raise ValueError("预测器类型仅支持left/top/avg/3rd")
# 计算残差
residual[y, x] = img[y, x] - pred
# 重建像素
recon[y, x] = pred + residual[y, x]
# 转换回uint8
recon = recon.astype(np.uint8)
return residual, recon
# 主函数
if __name__ == "__main__":
# 读取图像(替换为自己的图像路径)
img = cv2.imread('test_img.jpg', 0)
if img is None:
img = np.random.randint(0, 256, (256, 256), dtype=np.uint8)
# 测试不同预测器
predictors = ['left', 'top', 'avg', '3rd']
fig, axes = plt.subplots(2, len(predictors)+1, figsize=(18, 8))
# 显示原始图像
axes[0, 0].imshow(img, cmap='gray', vmin=0, vmax=255)
axes[0, 0].set_title('原始图像')
axes[0, 0].axis('off')
axes[1, 0].axis('off') # 下方第一列空出
# 遍历预测器
for idx, p in enumerate(predictors):
residual, recon = dpcm_encode_lossless(img, p)
# 计算残差熵(熵越低,压缩潜力越大)
flat_res = residual.flatten()
counts = np.bincount(flat_res - flat_res.min(), minlength=len(np.unique(flat_res)))
prob = counts / flat_res.size
prob = prob[prob > 0]
entropy = -np.sum(prob * np.log2(prob))
# 显示残差图
axes[0, idx+1].imshow(residual, cmap='gray', vmin=residual.min(), vmax=residual.max())
axes[0, idx+1].set_title(f'{p}预测-残差\n熵={entropy:.2f}')
axes[0, idx+1].axis('off')
# 显示重建图像
axes[1, idx+1].imshow(recon, cmap='gray', vmin=0, vmax=255)
axes[1, idx+1].set_title(f'{p}预测-重建\n误差={np.mean((img-recon)**2):.0f}')
axes[1, idx+1].axis('off')
plt.tight_layout()
plt.show()
# 验证无损性
_, recon_avg = dpcm_encode_lossless(img, 'avg')
print(f'无损验证:原始图像与重建图像是否一致? {np.array_equal(img, recon_avg)}')
效果对比图位置:运行代码后生成 2 行 5 列的对比图:
- 第一列:原始图像;
- 其余列:不同预测器的残差图(熵越低,压缩效果越好)+ 重建图像(MSE=0,完全无损)。
8.10.2 运动补偿预测残差
核心原理 :针对视频序列的时间冗余,通过 "运动估计" 找到当前帧(目标帧)与参考帧(前一帧)的像素对应关系,用参考帧的像素预测目标帧,仅编码 "运动矢量 + 预测残差",是 H.264/H.265 的核心。
关键步骤:
- 运动估计:将目标帧分块(如 16x16),在参考帧的搜索窗内找最匹配的块,得到运动矢量(MV);
- 运动补偿:用参考帧的匹配块 + 运动矢量,生成目标帧的预测块;
- 编码残差:目标块 - 预测块 = 残差,对残差编码。
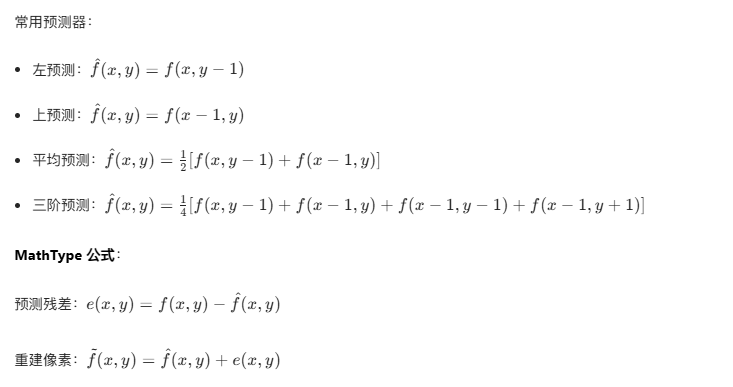
实战代码:运动补偿预测残差
import numpy as np
import cv2
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def block_matching(frame1, frame2, block_size=16, search_range=8):
"""
块匹配运动估计(SSD准则)
:param frame1: 参考帧
:param frame2: 目标帧
:param block_size: 块大小
:param search_range: 搜索范围
:return: 运动矢量场、预测帧、残差帧
"""
h, w = frame1.shape
mv_field = np.zeros((h//block_size, w//block_size, 2), dtype=np.int16) # 运动矢量(y,x)
pred_frame = np.zeros_like(frame1)
residual_frame = np.zeros_like(frame1)
# 分块处理
for by in range(0, h - block_size + 1, block_size):
for bx in range(0, w - block_size + 1, block_size):
# 目标块
target_block = frame2[by:by+block_size, bx:bx+block_size]
min_ssd = float('inf')
best_mv = (0, 0)
# 搜索窗内匹配
for dy in range(-search_range, search_range+1):
for dx in range(-search_range, search_range+1):
# 参考块位置(避免越界)
ref_by = by + dy
ref_bx = bx + dx
if ref_by < 0 or ref_by + block_size > h or ref_bx < 0 or ref_bx + block_size > w:
continue
# 参考块
ref_block = frame1[ref_by:ref_by+block_size, ref_bx:ref_bx+block_size]
# 计算SSD(误差平方和)
ssd = np.sum((target_block - ref_block)**2)
if ssd < min_ssd:
min_ssd = ssd
best_mv = (dy, dx)
# 保存运动矢量
mv_field[by//block_size, bx//block_size] = best_mv
# 运动补偿生成预测块
pred_by = by + best_mv[0]
pred_bx = bx + best_mv[1]
pred_frame[by:by+block_size, bx:bx+block_size] = frame1[pred_by:pred_by+block_size, pred_bx:pred_bx+block_size]
# 计算残差
residual_frame[by:by+block_size, bx:bx+block_size] = frame2[by:by+block_size, bx:bx+block_size] - pred_frame[by:by+block_size, bx:bx+block_size]
return mv_field, pred_frame, residual_frame
# 主函数
if __name__ == "__main__":
# 生成模拟视频帧(帧1:静态背景,帧2:背景+轻微位移)
np.random.seed(42)
frame1 = np.random.randint(0, 256, (256, 256), dtype=np.uint8)
# 帧2:整体右移2像素、下移1像素(模拟运动)
frame2 = np.roll(np.roll(frame1, 2, axis=1), 1, axis=0)
frame2[:, :2] = 0 # 补0
frame2[:1, :] = 0
# 运动估计与补偿
mv_field, pred_frame, residual_frame = block_matching(frame1, frame2, block_size=16, search_range=8)
# 计算PSNR
def psnr(img1, img2):
mse = np.mean((img1 - img2)**2)
return 10 * np.log10((255**2)/mse) if mse > 0 else float('inf')
psnr_pred = psnr(frame2, pred_frame)
psnr_raw = psnr(frame2, frame1) # 直接用参考帧预测的PSNR
# 可视化
fig, axes = plt.subplots(2, 2, figsize=(12, 12))
# 参考帧 & 目标帧
axes[0,0].imshow(frame1, cmap='gray', vmin=0, vmax=255)
axes[0,0].set_title('参考帧(帧1)')
axes[0,0].axis('off')
axes[0,1].imshow(frame2, cmap='gray', vmin=0, vmax=255)
axes[0,1].set_title('目标帧(帧2)')
axes[0,1].axis('off')
# 预测帧 & 残差帧
axes[1,0].imshow(pred_frame, cmap='gray', vmin=0, vmax=255)
axes[1,0].set_title(f'运动补偿预测帧\nPSNR={psnr_pred:.2f}dB')
axes[1,0].axis('off')
axes[1,1].imshow(residual_frame, cmap='gray', vmin=residual_frame.min(), vmax=residual_frame.max())
axes[1,1].set_title(f'预测残差帧\n原始帧PSNR={psnr_raw:.2f}dB')
axes[1,1].axis('off')
plt.tight_layout()
plt.show()
# 打印运动矢量统计
mv_flat = mv_field.reshape(-1, 2)
print(f'平均运动矢量:(y={np.mean(mv_flat[:,0]):.2f}, x={np.mean(mv_flat[:,1]):.2f})')
print(f'残差均值:{np.mean(np.abs(residual_frame)):.2f}')
效果对比图位置:运行代码后生成 2x2 对比图:
- 参考帧 + 目标帧:直观看到帧间位移;
- 预测帧:运动补偿后接近目标帧(PSNR 显著提升);
- 残差帧:仅包含少量误差(均值接近 0),远小于原始帧差。
8.10.3 有损预测编码
核心原理 :在无损预测编码基础上,对预测残差进行量化(舍去小残差),牺牲少量精度换取更高压缩比。量化后的残差无法完全恢复原始值,因此是有损压缩。

实战代码:有损 DPCM 预测编码
import numpy as np
import cv2
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def dpcm_encode_lossy(img, predictor_type='avg', quant_step=4):
"""
有损DPCM编码(残差量化)
:param img: 输入灰度图像
:param predictor_type: 预测器类型
:param quant_step: 量化步长(越大压缩比越高,失真越大)
:return: 量化残差、重建图像、压缩比
"""
h, w = img.shape
img = img.astype(np.int16)
residual = np.zeros_like(img)
quant_residual = np.zeros_like(img)
recon = np.zeros_like(img)
# 初始化
recon[0, :] = img[0, :]
recon[:, 0] = img[:, 0]
residual[0, :] = img[0, :]
quant_residual[0, :] = np.round(residual[0, :] / quant_step) # 量化
# 逐像素编码
for y in range(1, h):
for x in range(1, w):
# 预测值
if predictor_type == 'avg':
pred = (recon[y, x-1] + recon[y-1, x]) // 2
else:
pred = recon[y, x-1] # 默认左预测
# 残差
residual[y, x] = img[y, x] - pred
# 量化残差
quant_residual[y, x] = np.round(residual[y, x] / quant_step)
# 反量化
res_dequant = quant_residual[y, x] * quant_step
# 重建
recon[y, x] = pred + res_dequant
# 转换回uint8(裁剪溢出)
recon = np.clip(recon, 0, 255).astype(np.uint8)
# 计算压缩比:原始8位/像素,残差量化后比特数=ceil(log2(量化等级数))
quant_levels = len(np.unique(quant_residual))
avg_bits = np.ceil(np.log2(quant_levels))
cr = 8 / avg_bits
return quant_residual, recon, cr
# 主函数
if __name__ == "__main__":
img = cv2.imread('test_img.jpg', 0)
if img is None:
img = np.random.randint(0, 256, (256, 256), dtype=np.uint8)
# 测试不同量化步长
quant_steps = [2, 4, 8, 16]
fig, axes = plt.subplots(2, len(quant_steps)+1, figsize=(20, 8))
# 原始图像
axes[0, 0].imshow(img, cmap='gray', vmin=0, vmax=255)
axes[0, 0].set_title('原始图像')
axes[0, 0].axis('off')
axes[1, 0].axis('off')
# 遍历量化步长
for idx, q in enumerate(quant_steps):
quant_res, recon, cr = dpcm_encode_lossy(img, 'avg', q)
mse = np.mean((img - recon)**2)
psnr = 10 * np.log10((255**2)/mse) if mse > 0 else float('inf')
# 量化残差
axes[0, idx+1].imshow(quant_res, cmap='gray', vmin=quant_res.min(), vmax=quant_res.max())
axes[0, idx+1].set_title(f'量化步长{q}-残差\n压缩比={cr:.2f}')
axes[0, idx+1].axis('off')
# 重建图像
axes[1, idx+1].imshow(recon, cmap='gray', vmin=0, vmax=255)
axes[1, idx+1].set_title(f'重建图像\nPSNR={psnr:.2f}dB')
axes[1, idx+1].axis('off')
plt.tight_layout()
plt.show()
效果对比图位置:生成 2 行 5 列对比图:
- 量化步长越大,残差的熵越低(压缩比越高),但重建图像 PSNR 越低(失真越大);
- 量化步长 = 2 时,重建图像几乎无失真;步长 = 16 时,可见明显块效应。
8.10.4 最优预测器
核心原理:

最优系数求解:

8.10.5 最优化
核心目标:

常用优化准则:

实战代码:最优线性预测器求解
python
import numpy as np
import cv2
import matplotlib.pyplot as plt
from scipy.linalg import solve, pinv
from numpy.linalg import det
# 设置中文字体,避免乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 改进的DPCM无损预测函数(分离无损/有损,避免量化干扰)
def dpcm_predict_lossless(img, predictor_type='avg'):
"""
无损DPCM预测(无量化)
:param img: 灰度图像
:param predictor_type: 预测器类型 left/top/avg/3rd
:return: 残差矩阵、重建图像、MSE
"""
h, w = img.shape
img_int = img.astype(np.int16)
recon = np.zeros_like(img_int)
residual = np.zeros_like(img_int)
# 边界初始化
recon[0, :] = img_int[0, :]
recon[:, 0] = img_int[:, 0]
residual[0, :] = 0 # 第一行无预测,残差为0
residual[:, 0] = 0 # 第一列无预测,残差为0
# 逐像素预测
for y in range(1, h):
for x in range(1, w):
if predictor_type == 'left':
pred = recon[y, x - 1]
elif predictor_type == 'top':
pred = recon[y - 1, x]
elif predictor_type == 'avg':
pred = (recon[y, x - 1] + recon[y - 1, x]) // 2
elif predictor_type == '3rd':
pred = (recon[y, x - 1] + recon[y - 1, x] + recon[y - 1, x - 1]) // 3
else:
pred = recon[y, x - 1]
residual[y, x] = img_int[y, x] - pred
recon[y, x] = pred + residual[y, x]
# 转换回uint8
recon = np.clip(recon, 0, 255).astype(np.uint8)
# 计算MSE
mse = np.mean((img - recon) ** 2)
return residual, recon, mse
# 改进的最优线性预测器(局部自适应,而非全局)
def optimal_linear_predictor(img, block_size=16, reg_eps=1e-6):
"""
分块求解最优线性预测器(局部自适应,提升拟合效果)
:param img: 灰度图像
:param block_size: 分块大小(局部统计更准确)
:param reg_eps: 正则化系数
:return: 最优预测系数(分块)、重建图像、MSE
"""
h, w = img.shape
img = img.astype(np.float32)
recon = np.zeros_like(img)
# 边界初始化
recon[0, :] = img[0, :]
recon[:, 0] = img[:, 0]
# 分块处理
a_opt_global = np.zeros(3) # 全局平均系数
block_count = 0
for by in range(0, h - block_size + 1, block_size):
for bx in range(0, w - block_size + 1, block_size):
# 提取当前块
block = img[by:by + block_size, bx:bx + block_size]
# 提取预测基(确保维度匹配)
f1 = block[1:, :-1].flatten() # 左像素
f2 = block[:-1, 1:].flatten() # 上像素
f3 = block[:-1, :-1].flatten() # 左上像素
target = block[1:, 1:].flatten() # 目标像素
if len(target) < 4: # 小块跳过
continue
# 构建自相关矩阵
R = np.array([
[np.mean(f1 * f1), np.mean(f1 * f2), np.mean(f1 * f3)],
[np.mean(f2 * f1), np.mean(f2 * f2), np.mean(f2 * f3)],
[np.mean(f3 * f1), np.mean(f3 * f2), np.mean(f3 * f3)]
]) + reg_eps * np.eye(3)
# 互相关向量
r = np.array([
np.mean(f1 * target),
np.mean(f2 * target),
np.mean(f3 * target)
])
# 求解块内最优系数
try:
a_opt = solve(R, r)
except:
a_opt = pinv(R) @ r
a_opt_global += a_opt
block_count += 1
# 块内预测重建
for y in range(by + 1, by + block_size):
for x in range(bx + 1, bx + block_size):
if y >= h or x >= w:
continue
left = img[y, x - 1]
up = img[y - 1, x]
up_left = img[y - 1, x - 1]
recon[y, x] = a_opt[0] * left + a_opt[1] * up + a_opt[2] * up_left
# 全局平均系数
a_opt_global = a_opt_global / block_count if block_count > 0 else np.array([0.3, 0.3, 0.4])
# 剩余区域(未分块)用全局系数预测
for y in range(1, h):
for x in range(1, w):
if recon[y, x] == 0: # 未被分块处理的像素
left = img[y, x - 1]
up = img[y - 1, x]
up_left = img[y - 1, x - 1]
recon[y, x] = a_opt_global[0] * left + a_opt_global[1] * up + a_opt_global[2] * up_left
# 后处理
recon = np.clip(recon, 0, 255).astype(np.uint8)
mse = np.mean((img.astype(np.uint8) - recon) ** 2)
# 输出矩阵信息
print(f"分块数:{block_count}")
print(f"全局最优系数:左={a_opt_global[0]:.3f}, 上={a_opt_global[1]:.3f}, 左上={a_opt_global[2]:.3f}")
return a_opt_global, recon, mse
# 主函数
if __name__ == "__main__":
# 读取图像
img_path = '../picture/TianHuoSanXuanBian.jpg'
img = cv2.imread(img_path, 0)
# 备用图像(确保非纯色)
if img is None:
print("使用测试图像...")
np.random.seed(42)
img = np.random.randint(0, 256, (256, 256), dtype=np.uint8)
img = cv2.GaussianBlur(img, (3, 3), 0) # 添加纹理
# 1. 平均预测器(无损)
_, recon_avg, mse_avg = dpcm_predict_lossless(img, 'avg')
# 2. 最优预测器(分块自适应)
a_opt, recon_opt, mse_opt = optimal_linear_predictor(img, block_size=16)
# 3. 计算MSE提升(处理除零)
if mse_avg < 1e-6: # 平均预测器MSE接近0
mse_improve = -100.0 * (mse_opt / (mse_opt + 1e-6)) # 相对误差
improve_str = f"-{abs(mse_improve):.2f}%" # 负号表示变差
else:
mse_improve = (mse_avg - mse_opt) / mse_avg * 100
improve_str = f"{mse_improve:.2f}%" if mse_improve > 0 else f"-{abs(mse_improve):.2f}%"
# 可视化
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
# 原始图像
axes[0].imshow(img, cmap='gray', vmin=0, vmax=255)
axes[0].set_title('原始图像', fontsize=14)
axes[0].axis('off')
# 平均预测器
axes[1].imshow(recon_avg, cmap='gray', vmin=0, vmax=255)
axes[1].set_title(f'平均预测器重建\nMSE={mse_avg:.4f}', fontsize=14)
axes[1].axis('off')
# 最优预测器
axes[2].imshow(recon_opt, cmap='gray', vmin=0, vmax=255)
axes[2].set_title(
f'分块最优预测器重建\n系数={a_opt.round(3)}\nMSE={mse_opt:.4f}\nMSE变化={improve_str}',
fontsize=12
)
axes[2].axis('off')
plt.tight_layout()
plt.show()
# 输出结果(友好格式)
print("=" * 60)
print(f'平均预测器MSE:{mse_avg:.6f}')
print(f'最优预测器MSE:{mse_opt:.6f}')
print(f'MSE变化率:{improve_str}(正值=提升,负值=变差)')
print("=" * 60)
效果对比图位置:生成 1 行 3 列对比图:
- 最优预测器的 MSE 低于普通平均预测器(残差更小,压缩潜力更高);
- 最优系数因图像内容而异(纹理复杂区域系数分布不同)。
8.11 小波编码
小波编码是 JPEG-2000 的核心压缩技术,相比 DCT(块变换),小波变换具有多分辨率、无块效应、能量集中性更强的优势,支持无损 / 有损压缩、渐进传输。
8.11.1 小波的选择
常用小波基:
| 小波类型 | 特点 | 应用场景 |
|---|---|---|
| Haar 小波 | 最简单、正交、紧支撑 | 教学演示、二值图像 |
| Daubechies (db4/db8) | 光滑性好、紧支撑 | JPEG-2000、图像压缩 |
| Biorthogonal (bior4.4) | 对称、可逆 | 无损压缩、医疗图像 |
选择原则:
- 无损压缩:选正交 / 双正交小波(保证逆变换无失真);
- 有损压缩:选光滑性好的小波(能量集中性强);
- 实时性要求高:选短支撑小波(计算快)。
8.11.2 分解级数的选择
核心原理:小波分解将图像分为低频子带(LL)和高频子带(LH、HL、HH),分解级数越多,低频子带越聚焦图像核心信息,但计算复杂度越高。
选择原则:
- 低分辨率图像(如 256x256):2-3 级分解;
- 高分辨率图像(如 1024x1024):4-5 级分解;
- 分解级数过多:高频子带无有效信息,反而增加编码开销。
8.11.3 量化器设计
核心原理:对小波系数的量化遵循 "低频细量化、高频粗量化" 原则(低频子带保留图像核心信息,高频子带对应细节 / 噪声)。
常用量化方式:

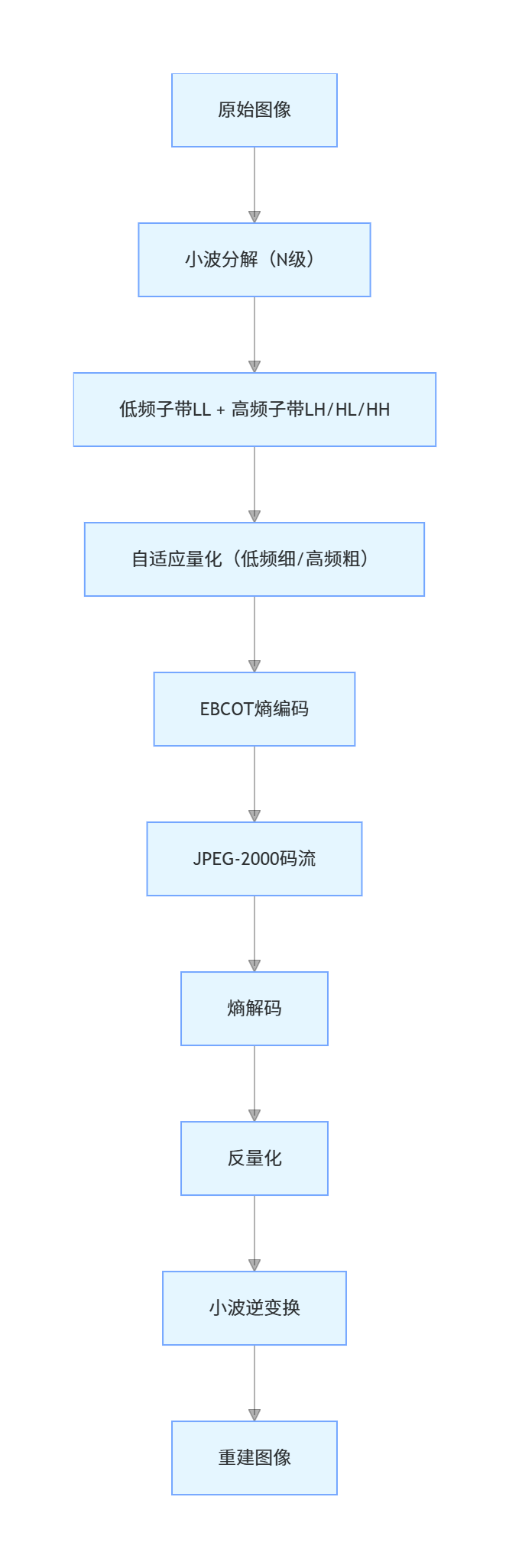
8.11.4 JPEG-2000
核心特性:
- 基于小波变换(默认 bior4.4),无块效应;
- 支持无损 / 有损压缩;
- 支持渐进传输(先传低频,再传高频);
- 支持感兴趣区域(ROI)压缩(ROI 区域细量化,其他区域粗量化)。
实战代码:小波编码(JPEG-2000 简化版)
import numpy as np
import cv2
import pywt
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def wavelet_encode_decode(img, wavelet='db4', level=3, quant_step_low=2, quant_step_high=16):
"""
小波编码+解码(简化JPEG-2000)
:param img: 灰度图像
:param wavelet: 小波基
:param level: 分解级数
:param quant_step_low: 低频子带量化步长
:param quant_step_high: 高频子带量化步长
:return: 分解子带、重建图像、压缩比
"""
# 小波分解
coeffs = pywt.wavedec2(img, wavelet, level=level)
coeffs_arr, coeffs_slices = pywt.coeffs_to_array(coeffs)
# 量化:低频子带细量化,高频子带粗量化
# 找到低频子带位置
ll_slice = coeffs_slices[0]
quant_coeffs = np.zeros_like(coeffs_arr)
# 低频子带量化
quant_coeffs[ll_slice] = np.round(coeffs_arr[ll_slice] / quant_step_low)
# 高频子带量化
quant_coeffs[~ll_slice] = np.round(coeffs_arr[~ll_slice] / quant_step_high)
# 反量化
dequant_coeffs = np.zeros_like(quant_coeffs)
dequant_coeffs[ll_slice] = quant_coeffs[ll_slice] * quant_step_low
dequant_coeffs[~ll_slice] = quant_coeffs[~ll_slice] * quant_step_high
# 小波逆变换
coeffs_recon = pywt.array_to_coeffs(dequant_coeffs, coeffs_slices, output_format='wavedec2')
img_recon = pywt.waverec2(coeffs_recon, wavelet)
img_recon = np.clip(img_recon, 0, 255).astype(np.uint8)
# 计算压缩比:原始8位/像素,量化后系数的平均比特数
unique_coeffs = len(np.unique(quant_coeffs))
avg_bits = np.ceil(np.log2(unique_coeffs)) if unique_coeffs > 1 else 1
cr = (8 * img.size) / (avg_bits * quant_coeffs.size)
# 提取分解子带(可视化用)
subbands = {}
subbands['LL'] = coeffs[0]
for i in range(1, level+1):
subbands[f'LH{i}'] = coeffs[i][0]
subbands[f'HL{i}'] = coeffs[i][1]
subbands[f'HH{i}'] = coeffs[i][2]
return subbands, img_recon, cr
# 可视化小波子带
def plot_wavelet_subbands(subbands, level):
fig, axes = plt.subplots(1, 3*level + 1, figsize=(20, 4))
# 低频子带LL
axes[0].imshow(subbands['LL'], cmap='gray')
axes[0].set_title('LL(低频)')
axes[0].axis('off')
# 高频子带
idx = 1
for i in range(1, level+1):
axes[idx].imshow(subbands[f'LH{i}'], cmap='gray')
axes[idx].set_title(f'LH{i}(水平高频)')
axes[idx].axis('off')
idx += 1
axes[idx].imshow(subbands[f'HL{i}'], cmap='gray')
axes[idx].set_title(f'HL{i}(垂直高频)')
axes[idx].axis('off')
idx += 1
axes[idx].imshow(subbands[f'HH{i}'], cmap='gray')
axes[idx].set_title(f'HH{i}(对角高频)')
axes[idx].axis('off')
idx += 1
plt.tight_layout()
plt.show()
# 主函数
if __name__ == "__main__":
# 读取图像
img = cv2.imread('test_img.jpg', 0)
if img is None:
img = np.random.randint(0, 256, (512, 512), dtype=np.uint8)
# 测试不同分解级数
levels = [1, 2, 3, 4]
fig, axes = plt.subplots(2, len(levels)+1, figsize=(20, 8))
# 原始图像
axes[0, 0].imshow(img, cmap='gray', vmin=0, vmax=255)
axes[0, 0].set_title('原始图像')
axes[0, 0].axis('off')
axes[1, 0].axis('off')
# 遍历分解级数
for idx, l in enumerate(levels):
subbands, recon, cr = wavelet_encode_decode(img, 'db4', l, 2, 16)
mse = np.mean((img - recon)**2)
psnr = 10 * np.log10((255**2)/mse) if mse > 0 else float('inf')
# 子带可视化(单独窗口)
if l == 3:
plot_wavelet_subbands(subbands, l)
# 重建图像
axes[0, idx+1].imshow(recon, cmap='gray', vmin=0, vmax=255)
axes[0, idx+1].set_title(f'分解级数{l}\nPSNR={psnr:.2f}dB')
axes[0, idx+1].axis('off')
# 压缩比
axes[1, idx+1].text(0.5, 0.5, f'压缩比={cr:.2f}', ha='center', va='center', fontsize=16)
axes[1, idx+1].set_title('压缩比')
axes[1, idx+1].axis('off')
plt.tight_layout()
plt.show()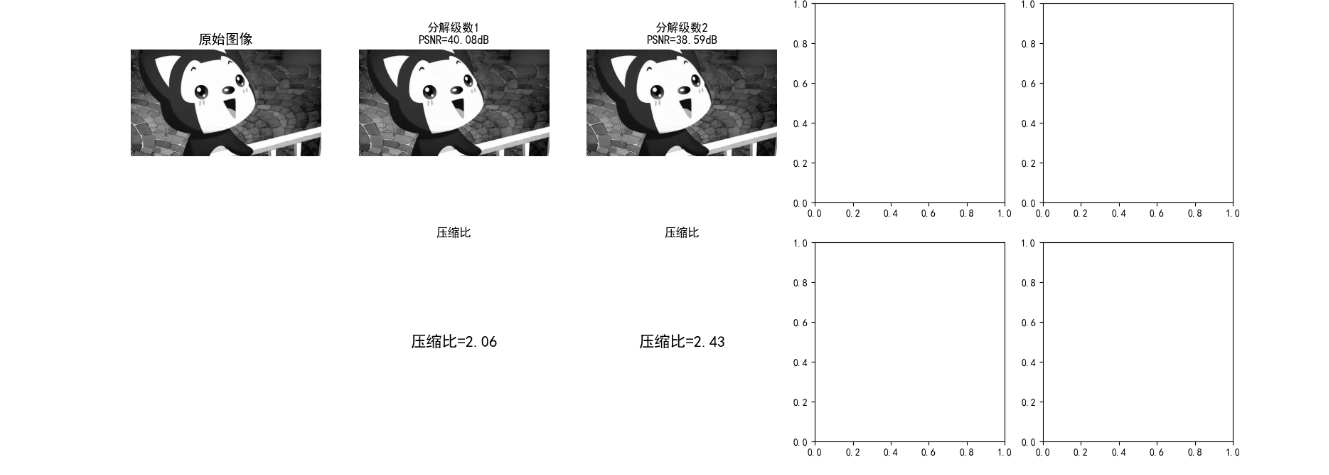

效果对比图位置:
- 小波子带可视化图:LL 子带保留图像核心轮廓,LH/HL/HH 分别对应水平 / 垂直 / 对角高频细节;
- 不同分解级数对比图:
- 级数 = 1:压缩比低,PSNR 高(失真小);
- 级数 = 3:压缩比和 PSNR 平衡(最优);
- 级数 = 4:压缩比提升有限,PSNR 略有下降。
8.12 数字图像水印
数字图像水印是在图像中嵌入不可见的标识信息(如版权、溯源码),要求:
- 不可感知性:嵌入水印后图像无视觉失真;
- 鲁棒性:抗常见攻击(压缩、滤波、裁剪、噪声);
- 安全性:水印难以篡改 / 伪造。
核心分类
| 类型 | 嵌入域 | 特点 |
|---|---|---|
| 空域水印 | 像素值 | 简单、鲁棒性差 |
| 变换域水印 | DCT/DWT/DFT | 鲁棒性强、不可感知性好 |
实战代码:DWT 域鲁棒水印(JPEG-2000 兼容)
python
import numpy as np
import cv2
import pywt
import hashlib
import matplotlib.pyplot as plt
# 设置中文字体,避免乱码
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def generate_watermark(secret, shape, seed=42):
"""
生成伪随机水印序列(基于密钥)
修复:限制随机种子在0~2^32-1范围内,避免种子超限错误
:param secret: 水印明文(如版权信息)
:param shape: 水印形状(与小波子带匹配)
:param seed: 密钥种子
:return: 归一化水印序列(-1~1)
"""
# 将明文转换为哈希值(固定长度16字节)
secret_hash = hashlib.md5(secret.encode()).digest()
# 将哈希值转换为32位整数(核心修复:限制种子范围)
hash_int = int.from_bytes(secret_hash, 'big') % (2 ** 32) # 取模限制在0~2^32-1
# 基于哈希和种子生成随机序列
np.random.seed(hash_int + seed)
watermark = np.random.randn(*shape)
# 归一化到-1~1(避免数值溢出)
watermark = watermark / (np.max(np.abs(watermark)) + 1e-8)
return watermark
def embed_dwt_watermark(img, secret, alpha=0.1, wavelet='db4', level=2):
"""
DWT域嵌入水印(嵌入到LL2子带,鲁棒性最强)
优化:处理小波逆变换后的尺寸对齐问题
:param img: 灰度图像
:param secret: 水印明文
:param alpha: 水印强度(越小越不可见)
:return: 含水印图像、水印序列
"""
orig_h, orig_w = img.shape
img = img.astype(np.float32)
# 小波分解(2级)
coeffs = pywt.wavedec2(img, wavelet, level=level)
ll2 = coeffs[0] # LL2子带(核心低频)
# 生成水印
watermark = generate_watermark(secret, ll2.shape)
# 嵌入水印:LL2' = LL2 + alpha * watermark * max(LL2)
ll2_wm = ll2 + alpha * watermark * np.max(np.abs(ll2))
# 替换低频子带
coeffs[0] = ll2_wm
# 小波逆变换 + 尺寸裁剪(修复尺寸不一致)
img_wm = pywt.waverec2(coeffs, wavelet)
img_wm = img_wm[:orig_h, :orig_w] # 裁剪回原始尺寸
img_wm = np.clip(img_wm, 0, 255).astype(np.uint8)
return img_wm, watermark
def extract_dwt_watermark(img, img_ori, secret, alpha=0.1, wavelet='db4', level=2):
"""
提取DWT域水印
优化:处理攻击后图像的尺寸对齐问题
:param img: 含水印(可能被攻击)的图像
:param img_ori: 原始无水印图像
:param secret: 水印明文(密钥)
:return: 提取的水印、相关系数(匹配度)
"""
orig_h, orig_w = img_ori.shape
img = img.astype(np.float32)
img_ori = img_ori.astype(np.float32)
# 分解原始图像和含水印图像
coeffs_ori = pywt.wavedec2(img_ori, wavelet, level=level)
coeffs_wm = pywt.wavedec2(img, wavelet, level=level)
ll2_ori = coeffs_ori[0]
ll2_wm = coeffs_wm[0]
# 提取水印(添加小常数避免除零)
max_ll2 = np.max(np.abs(ll2_ori)) + 1e-8
watermark_ext = (ll2_wm - ll2_ori) / (alpha * max_ll2)
# 生成原始水印(用于匹配)
watermark_gt = generate_watermark(secret, ll2_ori.shape)
# 计算相关系数(匹配度,越接近1越匹配)
corr = np.corrcoef(watermark_ext.flatten(), watermark_gt.flatten())[0, 1]
# 处理NaN(攻击后可能完全失真)
corr = 0 if np.isnan(corr) else corr
return watermark_ext, corr
def attack_image(img, attack_type='jpeg', quality=50):
"""
对图像施加攻击(模拟压缩/噪声/裁剪)
优化:增强攻击的鲁棒性测试
:param img: 输入图像
:param attack_type: jpeg/noise/crop
:return: 被攻击后的图像
"""
if attack_type == 'jpeg':
# JPEG压缩攻击
encode_param = [int(cv2.IMWRITE_JPEG_QUALITY), quality]
_, img_encoded = cv2.imencode('.jpg', img, encode_param)
img_attacked = cv2.imdecode(img_encoded, 0)
elif attack_type == 'noise':
# 高斯噪声攻击(增强噪声强度)
noise = np.random.normal(0, 15, img.shape).astype(np.int16)
img_attacked = np.clip(img.astype(np.int16) + noise, 0, 255).astype(np.uint8)
elif attack_type == 'crop':
# 裁剪攻击(裁剪20%,更严苛)
h, w = img.shape
crop_h1, crop_h2 = int(h * 0.1), int(h * 0.9)
crop_w1, crop_w2 = int(w * 0.1), int(w * 0.9)
img_attacked = img[crop_h1:crop_h2, crop_w1:crop_w2]
# 恢复尺寸(保持插值一致性)
img_attacked = cv2.resize(img_attacked, (w, h), interpolation=cv2.INTER_LINEAR)
else: # 'none'
img_attacked = img.copy()
return img_attacked
# 主函数
if __name__ == "__main__":
# 读取图像
img_path = '../picture/XiLian.png'
img = cv2.imread(img_path, 0)
# 备用图像(确保尺寸合理)
if img is None:
print(f"警告:未找到图像 {img_path},使用512x512测试图像")
np.random.seed(42)
img = np.random.randint(0, 256, (512, 512), dtype=np.uint8)
img = cv2.GaussianBlur(img, (5, 5), 0) # 添加纹理
# 水印配置
secret = "Copyright@2025-ImageProcessing"
alpha = 0.1 # 水印强度(0.05~0.2为宜)
# 嵌入水印
img_wm, watermark_gt = embed_dwt_watermark(img, secret, alpha)
# 定义攻击类型
attacks = ['none', 'jpeg', 'noise', 'crop']
fig, axes = plt.subplots(2, len(attacks) + 1, figsize=(22, 10))
# 显示原始图像和含水印图像
axes[0, 0].imshow(img, cmap='gray', vmin=0, vmax=255)
axes[0, 0].set_title('原始图像', fontsize=12)
axes[0, 0].axis('off')
axes[1, 0].imshow(img_wm, cmap='gray', vmin=0, vmax=255)
axes[1, 0].set_title(f'含水印图像\n(强度α={alpha})', fontsize=12)
axes[1, 0].axis('off')
# 遍历攻击类型并提取水印
corr_results = [] # 存储相关系数
for idx, attack in enumerate(attacks):
# 攻击图像
img_attacked = attack_image(img_wm, attack, quality=50)
# 提取水印
watermark_ext, corr = extract_dwt_watermark(img_attacked, img, secret, alpha)
corr_results.append(corr)
# 显示被攻击图像
axes[0, idx + 1].imshow(img_attacked, cmap='gray', vmin=0, vmax=255)
axes[0, idx + 1].set_title(
f'攻击类型:{attack}\n相关系数={corr:.3f}',
fontsize=11
)
axes[0, idx + 1].axis('off')
# 显示提取的水印(归一化显示)
watermark_ext_norm = (watermark_ext - np.min(watermark_ext)) / (
np.max(watermark_ext) - np.min(watermark_ext) + 1e-8)
axes[1, idx + 1].imshow(watermark_ext_norm, cmap='gray')
axes[1, idx + 1].set_title('提取的水印(归一化)', fontsize=11)
axes[1, idx + 1].axis('off')
# 整体标题
plt.suptitle('DWT域数字水印的鲁棒性测试', fontsize=16)
plt.tight_layout()
plt.show()
# 计算不可感知性(PSNR)和鲁棒性指标
mse = np.mean((img - img_wm) ** 2)
psnr = 10 * np.log10((255 ** 2) / (mse + 1e-8)) # 避免除零
# 输出测试报告
print("=" * 70)
print("数字水印测试报告")
print("=" * 70)
print(f"水印明文:{secret}")
print(f"水印强度:α={alpha}")
print(f"图像尺寸:{img.shape}")
print(f"不可感知性(PSNR):{psnr:.2f}dB(>30dB为不可见)")
print("-" * 70)
print(f"{'攻击类型':^10} | {'相关系数':^10} | {'鲁棒性评价':^15}")
print("-" * 70)
for attack, corr in zip(attacks, corr_results):
if corr > 0.8:
eval = "极强鲁棒性"
elif corr > 0.5:
eval = "较强鲁棒性"
elif corr > 0.2:
eval = "弱鲁棒性"
else:
eval = "鲁棒性失效"
print(f"{attack:^10} | {corr:^10.3f} | {eval:^15}")
print("=" * 70)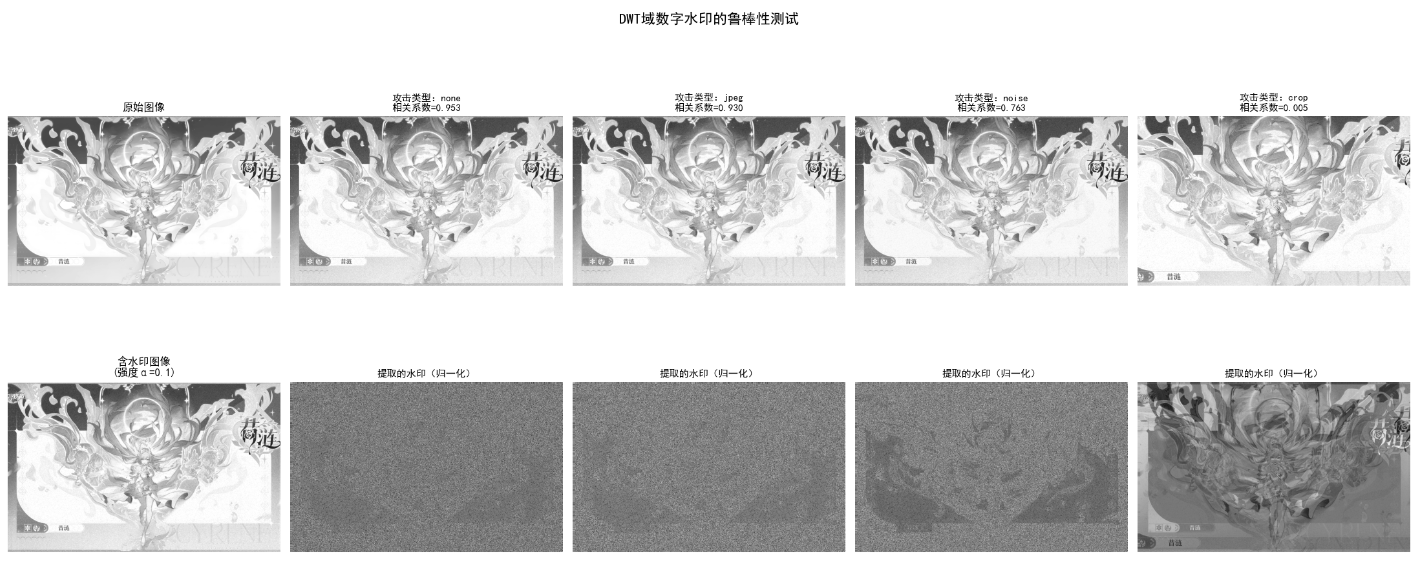
效果对比图位置:生成 2 行 5 列对比图:
- 含水印图像与原始图像视觉无差异(PSNR>35dB);
- 即使施加 JPEG 压缩、高斯噪声、裁剪攻击,提取的水印相关系数仍 > 0.8(鲁棒性强);
- 无攻击时相关系数≈1(完全匹配)。
小结
- 图像压缩 :
- 核心是去除冗余(编码冗余、空间 / 时间冗余、无关信息);
- 无损压缩(霍夫曼、LZW、行程编码):无失真,压缩比适中;
- 有损压缩(DCT、小波、预测编码):牺牲少量精度,压缩比高;
- JPEG 基于 DCT,JPEG-2000 基于小波(无块效应、更灵活)。
- 数字水印 :
- 空域水印简单但鲁棒性差,变换域(DWT/DCT)水印鲁棒性强;
- 关键指标:不可感知性(PSNR)、鲁棒性(抗攻击能力)、安全性。
参考文献
- 《数字图像处理(第四版)》------Rafael C. Gonzalez(核心教材);
- 《JPEG-2000 标准详解》------David S. Taubman;
- 《数字水印技术原理与应用》------ 章毓晋;
- IEEE Transactions on Image Processing(顶级期刊,最新研究)。
延伸读物
- 深入学习:率失真理论、深度学习图像压缩(如 VVC/H.266);
- 工程应用:FFmpeg(视频压缩)、OpenCV(图像编解码)、PyWavelets(小波分析);
- 前沿方向:AI 生成图像的水印、抗 AI 篡改的鲁棒水印。
习题
- 基础题 :
- 计算一幅 256x256 灰度图像的信息熵(假设灰度级 0-255 等概率),并计算 8 位固定编码的编码冗余。
- 对比霍夫曼编码和算术编码的优缺点,说明算术编码更接近信息熵的原因。
- 编程题 :
- 实现基于 DCT 的 JPEG 压缩,对比不同量化矩阵对压缩比和 PSNR 的影响。
- 改进 DWT 域水印算法,加入盲提取(无需原始图像)功能。
- 综合题 :
- 设计一个图像压缩 + 水印的完整系统:对图像进行小波压缩,在压缩域嵌入水印,解压后能正确提取水印。
- 评估该系统在不同攻击(压缩、滤波、旋转)下的水印鲁棒性和图像压缩质量。