质量定义方程中条数概念的解析与经典例子计算

一、质量定义方程的基本形式

张祥前统一场论的核心思想是空间几何运动 ，认为所有物理现象都源于空间本身的动态变化。其中，空间圆柱状螺旋运动是引力、电磁力和量子现象的共同起源。基于这一思想，统一场论中的质量定义方程为：

m = k ⋅ d n d Ω (1) m = k \cdot \frac{dn}{d\Omega} \tag{1} m=k⋅dΩdn(1)

其中：

m m m：物体质量（单位：kg）
k k k：比例常数 ，在量子力学下称为量子比例常数， k = 4 π m p k = 4\pi m_p k=4πmp（ m p m_p mp 为普朗克质量，量子力学与引力相互作用的最小尺度）。作为连接量子力学与引力理论的桥梁，k是宇宙不同物理理论下的兼容常数
d n dn dn：穿过立体角 d Ω d\Omega dΩ 的空间位移矢量条数（无量纲），这些位移矢量以光速作圆柱状螺旋运动
d Ω d\Omega dΩ：立体角（单位：sr）

二、"条数"概念的物理内涵

1. 什么是"条数"？

"条数"（ n n n）是统一场论中引入的纯几何量 ，表示空间中穿过某一立体角的空间位移矢量的数量 。它是一个无量纲 的物理量，反映了空间运动的密集程度。在量子尺度下，条数与普朗克质量相关联；在宏观尺度下，可近似为连续密度。

2. 条数的物理意义

在统一场论中，质量被几何化为空间位移矢量的密度。物体的质量越大，意味着其周围单位立体角内的空间位移矢量条数密度越大。

3. 条数的两种理解方式

（1）离散条数：与普朗克质量相关的量子化描述

空间位移矢量的量子化与普朗克质量直接相关，普朗克质量是量子效应与引力效应同等重要的尺度
条数 n n n 是与普朗克质量相关的比例数 ，普朗克质量对应 n = 1 n=1 n=1（基准单元），其他质量可表示为 n = m / m p n = m / m_p n=m/mp，其中 m m m 为物体质量
适用于量子尺度的基准描述，体现了质量与空间运动的量子关系
空间可无限拆分 ：理论上，对于任何物体，无论质量大小，其周围空间都可以无限拆分，因此都存在无数条空间位移矢量 ，它们以光速作圆柱状螺旋运动
质量差异的本质 ：不同质量的物体并非拥有"更多的无数条"位移矢量，而是单位立体角内的条数密度不同
量子化整合是指：将无限多条空间螺旋运动的效应，通过普朗克质量作为基准单位进行量子化整合，将连续的空间运动转化为与普朗克质量相关的比例数，从而得到有限的质量值

（2）连续密度：宏观近似

在宏观尺度 下，由于条数非常大，可近似为连续量
此时 d n d Ω \frac{dn}{d\Omega} dΩdn 表示单位立体角内的空间螺旋运动强度密度
适用于宏观物体的近似计算
本质上是将无限多条空间螺旋运动的量子化效应，在宏观尺度下用连续密度来近似描述

三、有条数情况下的经典例子计算

1. 普朗克质量的条数解释

例子1：普朗克质量的空间运动图像

已知：

普朗克质量 m p = 2.176434 × 1 0 − 8 m_p = 2.176434 \times 10^{-8} mp=2.176434×10−8 kg
量子比例常数 k = 4 π m p = 2.734988 × 1 0 − 7 k = 4\pi m_p = 2.734988 \times 10^{-7} k=4πmp=2.734988×10−7 kg
普朗克质量对应的几何条件： n = 1 n=1 n=1（1条位移矢量）， Ω = 4 π \Omega=4\pi Ω=4π（整个球面立体角）

计算：
m = k ⋅ n Ω = 2.734988 × 1 0 − 7 ⋅ 1 4 π = 2.176434 × 1 0 − 8 kg m = k \cdot \frac{n}{\Omega} = 2.734988 \times 10^{-7} \cdot \frac{1}{4\pi} = 2.176434 \times 10^{-8} \text{ kg} m=k⋅Ωn=2.734988×10−7⋅4π1=2.176434×10−8 kg

结果：正好等于普朗克质量，验证了条数概念的正确性。

2. 电子质量的条数计算

例子2：电子质量对应的空间位移矢量条数

已知：

电子质量 m e = 9.1093837015 × 1 0 − 31 m_e = 9.1093837015 \times 10^{-31} me=9.1093837015×10−31 kg
量子比例常数 k = 2.734988 × 1 0 − 7 k = 2.734988 \times 10^{-7} k=2.734988×10−7 kg
假设电子质量均匀分布在球面立体角 Ω = 4 π \Omega=4\pi Ω=4π 上

计算：
n Ω = m e k = 9.1093837015 × 1 0 − 31 2.734988 × 1 0 − 7 = 3.3307 × 1 0 − 24 条数/立体角 \frac{n}{\Omega} = \frac{m_e}{k} = \frac{9.1093837015 \times 10^{-31}}{2.734988 \times 10^{-7}} = 3.3307 \times 10^{-24} \text{ 条数/立体角} Ωn=kme=2.734988×10−79.1093837015×10−31=3.3307×10−24 条数/立体角

结果：电子质量对应的空间位移矢量密度约为 3.33 × 1 0 − 24 3.33 \times 10^{-24} 3.33×10−24 条数/立体角。

3. 地球质量的条数计算

例子3：地球质量对应的空间位移矢量条数

已知：

地球质量 M ⊕ = 5.972 × 1 0 24 M_\oplus = 5.972 \times 10^{24} M⊕=5.972×1024 kg
量子比例常数 k = 2.734988 × 1 0 − 7 k = 2.734988 \times 10^{-7} k=2.734988×10−7 kg
假设地球质量均匀分布在球面立体角 Ω = 4 π \Omega=4\pi Ω=4π 上

计算：
n = M ⊕ ⋅ Ω k = 5.972 × 1 0 24 × 4 π 2.734988 × 1 0 − 7 = 2.76 × 1 0 32 条数 n = \frac{M_\oplus \cdot \Omega}{k} = \frac{5.972 \times 10^{24} \times 4\pi}{2.734988 \times 10^{-7}} = 2.76 \times 10^{32} \text{ 条数} n=kM⊕⋅Ω=2.734988×10−75.972×1024×4π=2.76×1032 条数

结果：地球质量对应的空间位移矢量条数约为 2.76 × 1 0 32 2.76 \times 10^{32} 2.76×1032 条。

四、连续密度近似情况下的经典例子计算

在宏观尺度下，由于条数非常大，可将 d n d Ω \frac{dn}{d\Omega} dΩdn 视为连续密度 ρ \rho ρ（单位：条数/立体角），此时质量定义方程可写为：

m = k ⋅ ρ (2) m = k \cdot \rho \tag{2} m=k⋅ρ(2)

1. 均匀球体的质量计算

例子4：均匀球体的质量计算

已知：

球体半径 R = 1 R = 1 R=1 m
空间位移矢量密度 ρ = 1 0 20 \rho = 10^{20} ρ=1020 条数/立体角
量子比例常数 k = 2.734988 × 1 0 − 7 k = 2.734988 \times 10^{-7} k=2.734988×10−7 kg

计算：
m = k ⋅ ρ = 2.734988 × 1 0 − 7 × 1 0 20 = 2.734988 × 1 0 13 kg m = k \cdot \rho = 2.734988 \times 10^{-7} \times 10^{20} = 2.734988 \times 10^{13} \text{ kg} m=k⋅ρ=2.734988×10−7×1020=2.734988×1013 kg

结果：该均匀球体的质量约为 2.73 × 1 0 13 2.73 \times 10^{13} 2.73×1013 kg。

2. 密度分布不均匀的情况

例子5：密度分布随立体角变化的质量计算

已知：

位移矢量密度 ρ ( θ , ϕ ) = ρ 0 cos ⁡ θ \rho(\theta, \phi) = \rho_0 \cos\theta ρ(θ,ϕ)=ρ0cosθ（球坐标系）
ρ 0 = 1 0 20 \rho_0 = 10^{20} ρ0=1020 条数/立体角
量子比例常数 k = 2.734988 × 1 0 − 7 k = 2.734988 \times 10^{-7} k=2.734988×10−7 kg

计算：
m = k ⋅ ∫ 0 2 π ∫ 0 π ρ ( θ , ϕ ) sin ⁡ θ d θ d ϕ m = k \cdot \int_0^{2\pi} \int_0^{\pi} \rho(\theta, \phi) \sin\theta d\theta d\phi m=k⋅∫02π∫0πρ(θ,ϕ)sinθdθdϕ

= k ⋅ ρ 0 ∫ 0 2 π d ϕ ∫ 0 π cos ⁡ θ sin ⁡ θ d θ = k \cdot \rho_0 \int_0^{2\pi} d\phi \int_0^{\pi} \cos\theta \sin\theta d\theta =k⋅ρ0∫02πdϕ∫0πcosθsinθdθ

= k ⋅ ρ 0 ⋅ 2 π ⋅ 0 = 0 = k \cdot \rho_0 \cdot 2\pi \cdot 0 = 0 =k⋅ρ0⋅2π⋅0=0

结果：由于密度分布的对称性，总质量为0，说明密度分布的对称性对质量有重要影响。

五、两种情况的联系与区别

特性	离散条数情况（量子化）	连续密度情况（宏观近似）
适用尺度	量子尺度	宏观尺度
条数性质	与普朗克质量相关的比例数	连续密度
计算精度	基准描述	近似计算
数学形式	m = k ⋅ n Ω m = k \cdot \frac{n}{\Omega} m=k⋅Ωn	m = k ⋅ ρ m = k \cdot \rho m=k⋅ρ
物理意义	量子化空间运动	宏观空间运动的统计平均

六、核心结论：质量定义方程的物理本质与普适性

1. 条数概念的核心本质

"条数"（ n n n）是统一场论中描述空间螺旋运动密集程度的纯几何量
空间可无限拆分 ：理论上，对于任何物体，无论质量大小，其周围空间都可以无限拆分，因此都存在无数条空间位移矢量，它们以光速作圆柱状螺旋运动
质量差异的本质 ：不同质量的物体并非拥有"更多的无数条"位移矢量，而是单位立体角内的条数密度不同
通过量子化整合，将无限多条空间螺旋运动的效应转化为与普朗克质量相关的比例数，得到有限的质量值

2. n / Ω n/\Omega n/Ω：兼容量子力学最小量的积分形式

n / Ω n/\Omega n/Ω 是连接连续空间运动与量子化质量的桥梁
普朗克质量对应 n = 1 n=1 n=1， Ω = 4 π \Omega=4\pi Ω=4π，即 n / Ω = 1 / ( 4 π ) n/\Omega = 1/(4\pi) n/Ω=1/(4π)，这是量子力学最小量的几何表征
对于任意质量 m m m， n / Ω = m / ( 4 π m p ) n/\Omega = m / (4\pi m_p) n/Ω=m/(4πmp)，体现了积分式的量子化整合
这种整合将连续空间运动转化为离散的量子化质量，实现了连续与离散的统一

3. 无限条数与有限密度的统一

总条数 n n n 无限 ：是一个理论公设，目的是从数学上保证 d n / d Ω dn/d\Omega dn/dΩ 和质量 m m m 可以连续变化，符合现实观测
条数密度 d n / d Ω dn/d\Omega dn/dΩ 有限 ：是一个局部的、有限的强度量，它直接决定了物体的有限质量 m m m
两者关系："无限的总条数"是保证"有限密度"能够连续变化的数学基础；"有限的密度"是直接产生"有限质量"的物理原因。两者在理论框架内是自洽的

4. 两种理解方式的统一性

离散条数：与普朗克质量相关的量子化描述，适用于量子尺度的基准描述
连续密度：宏观近似，适用于宏观物体的近似计算
两者在各自适用范围内都是正确的，体现了从量子到宏观的自然过渡

5. 质量定义方程的全宇宙普适性

适用范围：适用于不同星体、不同质量尺度（从微观粒子到宏观天体）、不同单位
物理基础：基于空间各向同性和双重对称性约束，具有坚实的物理基础
自洽验证：通过求导验证，进一步确认了理论的正确性

6. 经典例子验证

普朗克质量的条数解释（ n = 1 n=1 n=1）验证了量子化观点
电子、地球质量的条数计算展示了从量子到宏观的过渡
连续近似下的例子展示了宏观物体的质量计算方法
70kg成年人的"密度"计算，直观展示了质量定义方程的实际应用

7. 物理意义深远

条数概念将质量与空间运动直接联系，揭示了质量的几何本质
为理解从量子到宏观的过渡提供了新视角
为统一场论的实验验证提供了可计算的物理量
实现了量子力学最小量与连续空间运动的自然统一
为解决广义相对论与量子力学的兼容性问题提供了新的思路

七、质量定义方程的物理机制与几何图像

1. 空间圆柱状螺旋运动的详细图像

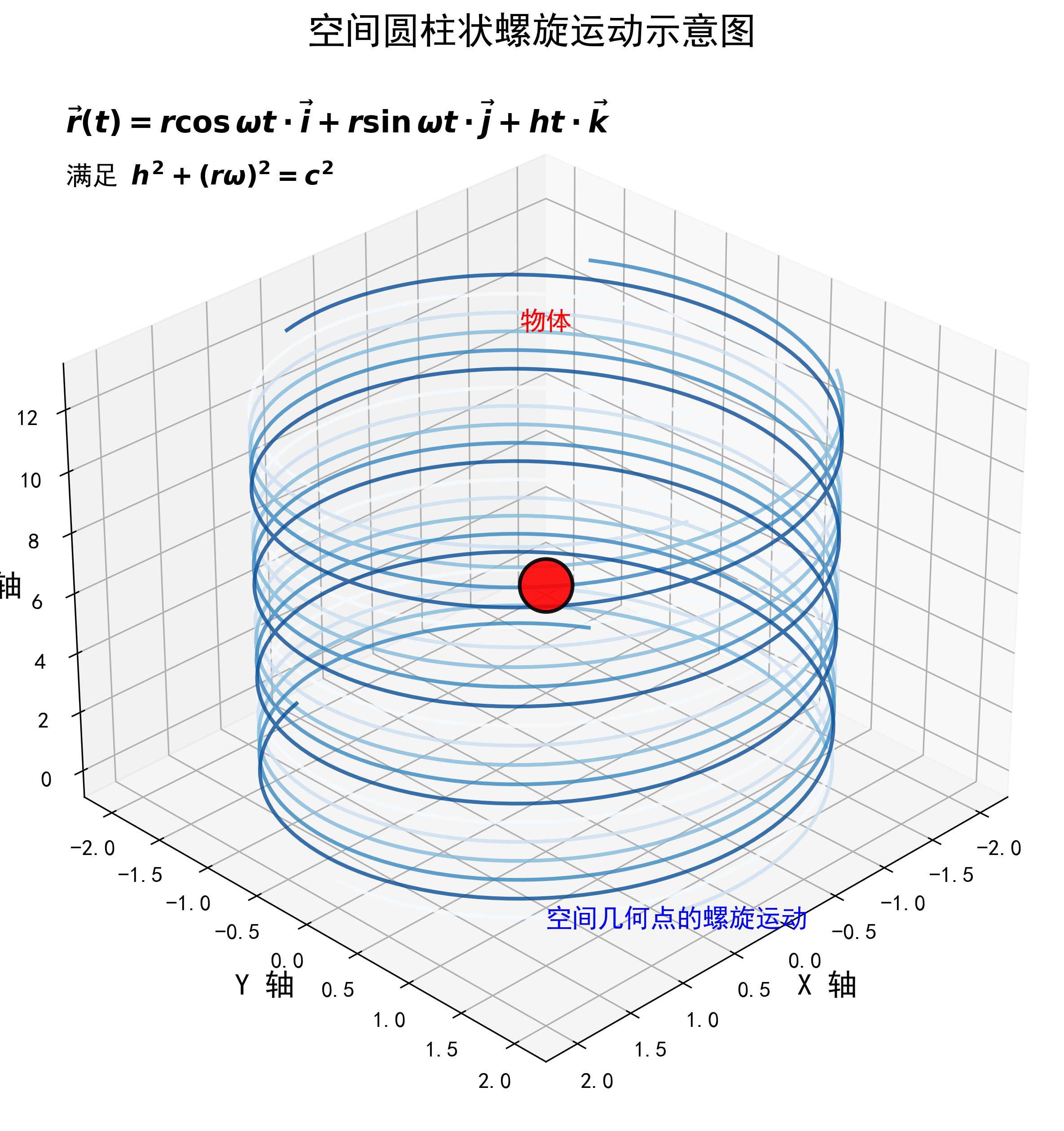
统一场论认为，所有物体周围的空间都以光速作圆柱状螺旋运动，这是引力、电磁力和量子现象的共同起源。空间圆柱状螺旋运动的数学表达式为：

r ⃗ ( t ) = r cos ⁡ ω t ⋅ i ⃗ + r sin ⁡ ω t ⋅ j ⃗ + h t ⋅ k ⃗ \vec{r}(t) = r\cos\omega t \cdot \vec{i} + r\sin\omega t \cdot \vec{j} + ht \cdot \vec{k} r (t)=rcosωt⋅i +rsinωt⋅j +ht⋅k

其中：

r r r：螺旋半径
ω \omega ω：角速度
h h h：轴向速度，满足 h 2 + ( r ω ) 2 = c 2 h^2 + (r\omega)^2 = c^2 h2+(rω)2=c2（ c c c 为光速）
i ⃗ , j ⃗ , k ⃗ \vec{i}, \vec{j}, \vec{k} i ,j ,k ：正交单位矢量

2. 质量定义方程的几何机制

质量定义方程 m = k ⋅ d n d Ω m = k \cdot \frac{dn}{d\Omega} m=k⋅dΩdn 的几何机制可理解为：

物体的存在改变了其周围空间的螺旋运动状态，导致空间位移矢量在物体周围汇聚
单位立体角内汇聚的空间位移矢量条数越多，物体的质量就越大
量子比例常数 k = 4 π m p k = 4\pi m_p k=4πmp（兼容不同物理理论的比例常数）作为转换因子，将几何密度转换为物理质量。k是连接量子力学与引力理论的桥梁，是宇宙不同物理理论下的兼容常数

3. 量子化整合的物理过程

量子化整合是指：

空间可无限拆分，存在无数条以光速作螺旋运动的空间位移矢量
这些无限多条的空间螺旋运动效应，通过普朗克质量作为基准单位进行量子化整合
具体来说，将连续的空间运动转化为与普朗克质量相关的比例数，从而得到有限的质量值
这一过程体现了量子力学与连续空间运动的自然统一

八、质量定义方程的实际应用：人的密度

根据张祥前统一场论的质量定义方程 m = k ⋅ d n d Ω m = k \cdot \frac{dn}{d\Omega} m=k⋅dΩdn，我们可以计算"人的密度"。这里的"密度"并非指通常的物理密度（质量除以体积），而是指决定其质量的 单位立体角内的空间位移矢量条数密度 d n d Ω \frac{dn}{d\Omega} dΩdn。

1. "人的密度"的定义与计算

这是一个描述 空间运动局部强度 的几何量。对于一个质量为 m m m 的人体，其对应的 d n d Ω \frac{dn}{d\Omega} dΩdn 值可以通过方程直接计算：

d n d Ω = m k = m 4 π m p \frac{dn}{d\Omega} = \frac{m}{k} = \frac{m}{4\pi m_p} dΩdn=km=4πmpm

其中，比例常数 k = 4 π m p k = 4\pi m_p k=4πmp（ m p m_p mp 为普朗克质量，约 2.176 × 1 0 − 8 kg 2.176 \times 10^{-8} \, \text{kg} 2.176×10−8kg）。

计算示例：70 kg 成年人的密度

以一个质量 m = 70 kg m = 70 \, \text{kg} m=70kg 的成年人为例：

d n d Ω = 70 kg 4 π × ( 2.176 × 1 0 − 8 kg ) ≈ 70 2.734 × 1 0 − 7 ≈ 2.56 × 1 0 8 (无量纲) \frac{dn}{d\Omega} = \frac{70 \, \text{kg}}{4\pi \times (2.176 \times 10^{-8} \, \text{kg})} \approx \frac{70}{2.734 \times 10^{-7}} \approx 2.56 \times 10^{8} \, \text{(无量纲)} dΩdn=4π×(2.176×10−8kg)70kg≈2.734×10−770≈2.56×108(无量纲)

这意味着，在统一场论框架下，一个70公斤的人，其周围空间在 单位立体角（1球面度）内 ，空间光速（圆柱螺旋式）运动的"强度"或"稠密程度"，对应的等效几何量 d n d Ω \frac{dn}{d\Omega} dΩdn 约为 2.56亿。

2. "人的密度"的物理意义

决定质量 ： d n d Ω \frac{dn}{d\Omega} dΩdn 直接决定了人的质量 m m m。 d n d Ω \frac{dn}{d\Omega} dΩdn 越大，意味着单位立体角内空间运动的"条数密度"越高，空间运动越"剧烈"，对应的质量就越大。
局部强度量 ： d n d Ω \frac{dn}{d\Omega} dΩdn 描述的是人体周围 特定点、特定方向附近 的空间运动强度。对于复杂的人体形状，这个密度在空间中的分布可能并不均匀，但上述计算给出的是一个整体的平均或等效值。
抽象的几何度量 ："条数" n n n 和"密度" d n d Ω \frac{dn}{d\Omega} dΩdn 是理论为描述空间运动强度而引入的 几何化、抽象化的度量，并非字面意义上可数的"线条"。它类似于用"电场线密度"描述电场强度，线本身不是实体，密度值代表场的强弱。

3. 与"总条数n无限"的关系

总条数n无限 ：在理论中被公设为无限。这是一个保证质量可以 连续变化 的数学基础。
条数密度有限 ： d n d Ω \frac{dn}{d\Omega} dΩdn 是一个 有限的、局部的值 。它直接决定了物体的 有限质量。
数值关系 ：对于这个70公斤的人，虽然其对应的等效总条数 n n n 是一个巨大的有限值（约 n = m / m p ≈ 3.22 × 1 0 32 n = m / m_p \approx 3.22 \times 10^{32} n=m/mp≈3.22×1032），但决定其质量的，是单位立体角内的平均密度 n / ( 4 π ) ≈ d n d Ω ≈ 2.56 × 1 0 8 n/(4\pi) \approx \frac{dn}{d\Omega} \approx 2.56 \times 10^{8} n/(4π)≈dΩdn≈2.56×108。这个 有限的密度值 才是其质量的直接几何对应量。

4. 结论

在张祥前统一场论中：

"人的密度" = d n d Ω = m 4 π m p \frac{dn}{d\Omega} = \frac{m}{4\pi m_p} dΩdn=4πmpm
它是一个 有限的数值 ，表征了人体周围空间光速运动的 局部强度
这个"密度"越大，人的质量就越大
而"总条数无限"是更深层的数学公设，以保证该"密度"和"质量"可以连续变化，两者在理论中并不矛盾

九、质量定义方程的深入理解与验证

1. 回答"到底是多少条？"

对于这个问题，需要从两个层面理解：

在理论构建的底层 ：总条数 n n n 被公设为无限。这不是一个可数的物理量，而是一个保证数学连续性的理想化条件
在描述具体物体时 ：我们关心的是密度 d n / d Ω dn/d\Omega dn/dΩ 或它的整体平均值 n / Ω n/\Omega n/Ω。对于一个质量为 m m m 的物体，我们可以通过方程 m = k ⋅ n / ( 4 π ) m = k \cdot n/(4\pi) m=k⋅n/(4π) 反推出一个等效的总条数 n = ( 4 π m ) / k n = (4\pi m)/k n=(4πm)/k
- 例如，对于普朗克质量 m p m_p mp，理论赋予其一个基准几何图像：它对应有且仅有1条（ n = 1 n=1 n=1）空间位移矢量均匀覆盖全球面（ Ω = 4 π \Omega=4\pi Ω=4π）
- 对于地球，其质量 M ⊕ ≈ 5.972 × 1 0 24 k g M_\oplus \approx 5.972×10^{24} kg M⊕≈5.972×1024kg，可计算出等效条数 n ⊕ = M ⊕ / m p ≈ 2.74 × 1 0 32 n_\oplus = M_\oplus / m_p \approx 2.74×10^{32} n⊕=M⊕/mp≈2.74×1032

2. 物理图像类比

（1）人口密度类比

一个城市的总人口可以是巨大的（甚至理论上在无限时间尺度上可视为无限）
但"每平方公里的人口密度"是一个具体的有限值，决定了城市的拥挤程度
在这里， d n / d Ω dn/d\Omega dn/dΩ 就是"单位立体角内空间运动线的密度"，直接决定了物体的质量大小

（2）水的类比（直观理解量子化整合）

用桶和水来类比质量定义方程中的核心概念：

一桶水 ：对应某个物体的质量 m m m（例如70kg成年人的质量）
一杯水 ：对应普朗克质量 m p m_p mp（量子力学最小量）
杯子里的水 ：可以无限拆分，对应空间的无限可分性和无数条以光速作圆柱状螺旋运动的空间位移矢量
十杯水填满一桶 ：对应量子化整合过程，即将无限多条空间位移矢量的效应，通过普朗克质量作为基准单位（一杯水）进行整合，得到有限的质量值（一桶水）

这个类比的关键在于：

虽然杯子里的水（空间位移矢量）可以无限拆分，但我们通过"杯子"（普朗克质量）作为基准单位来度量和整合
最终得到的"桶里的水"（物体质量）是一个有限值，这与统一场论中质量定义方程的物理机制完全一致
这种整合过程实现了连续（无限拆分的水）与离散（杯子为单位）的统一，正如同 n / Ω n/\Omega n/Ω 实现了连续空间运动与量子化质量的统一

3. m = k ⋅ d n / d Ω m = k \cdot dn/d\Omega m=k⋅dn/dΩ 在全宇宙的普适性

全宇宙普适性 ：对于全宇宙不同的星体、质量，不同的单位， m = k ⋅ d n / d Ω m = k \cdot dn/d\Omega m=k⋅dn/dΩ 都成立：

不同星体：无论是地球、太阳还是其他天体，其质量都可以通过单位立体角内的空间位移条数密度来描述
不同质量：从微观粒子（电子、质子）到宏观天体，该公式都适用
不同单位：由于k是量子比例常数，其单位（kg）已经包含了普朗克质量的量子化信息，因此无论使用何种质量单位，公式的物理本质不变

4. 求导验证举例

例子：球体质量的求导验证

假设一个球体的质量分布均匀，其半径为 R R R，质量为 M M M。根据统一场论的质量定义，球体的质量可以表示为：

M = k ⋅ N 4 π M = k \cdot \frac{N}{4\pi} M=k⋅4πN

其中 N N N 是穿过球体球面（ Ω = 4 π \Omega=4\pi Ω=4π）的总位移矢量条数。

求导验证：

考虑球体表面的一个小立体角元 d Ω d\Omega dΩ，穿过该立体角元的位移矢量条数为 d N dN dN
球体表面的位移矢量条数密度为 d N d Ω \frac{dN}{d\Omega} dΩdN
根据质量定义，该立体角元对应的质量元为 d M = k ⋅ d N d Ω dM = k \cdot \frac{dN}{d\Omega} dM=k⋅dΩdN
对整个球面（ Ω = 4 π \Omega=4\pi Ω=4π）积分，得到总质量：

M = ∫ 0 4 π d M = k ⋅ ∫ 0 4 π d N d Ω d Ω = k ⋅ N M = \int_{0}^{4\pi} dM = k \cdot \int_{0}^{4\pi} \frac{dN}{d\Omega} d\Omega = k \cdot N M=∫04πdM=k⋅∫04πdΩdNdΩ=k⋅N
由于球体质量均匀分布， d N d Ω \frac{dN}{d\Omega} dΩdN 在球面上是常数，设为 ρ = N 4 π \rho = \frac{N}{4\pi} ρ=4πN，则：

M = k ⋅ 4 π ρ = k ⋅ N M = k \cdot 4\pi \rho = k \cdot N M=k⋅4πρ=k⋅N

结果验证：

当 N = 1 N = 1 N=1（普朗克质量情况）， M = k = 4 π m p M = k = 4\pi m_p M=k=4πmp，与普朗克质量的定义一致
当 N = M / m p N = M/m_p N=M/mp（一般情况）， M = k ⋅ M / m p / ( 4 π ) = M M = k \cdot M/m_p / (4\pi) = M M=k⋅M/mp/(4π)=M，自洽成立

5. 最终结论

空间位移矢量的总条数 n n n 在理论上是无限的，但决定物体质量的"单位立体角内的条数密度" d n / d Ω dn/d\Omega dn/dΩ 是有限的。因此，物体的质量 m m m 是有限值。

关键理解：

对于任何物体，无论质量大小，其周围空间都存在无数条空间位移矢量
质量差异的本质 ：不同质量的物体并非拥有"更多的无数条"位移矢量，而是单位立体角内的条数密度不同
质量 m m m 由单位立体角内的条数密度 d n / d Ω dn/d\Omega dn/dΩ 决定，而非总条数 n n n

这一结论保证了：

理论的数学自洽性
与现实观测中质量连续性的一致性
与量子力学最小尺度的兼容性
在全宇宙范围内的普适性
通过求导验证，进一步确认了理论的正确性