一、决策树
概念:决策树通过对训练样本的学习,并建立分类规则,然后依据分类规则对新样本数据进行分类预测,属于有监督学习。
核心:所有数据从根节点一步一步落到叶子节点
什么是有监督学习,也就是是否有y(标签结果),在上文学习逻辑回归的时候,我们会设置x和y,其中x为特征,y是结果标签,有监督学习就是有y参与计算,线性回归和逻辑回归都用参加了计算。无监督学习自然就是不需要y参与计算就做出分类。自然无监督学习的模型准确率都比较低。
一般y结果标签都是人为标记的,当没有标记的时候会用到无监督学习,实际问题中监督学习和无监督学习都是一起使用的。
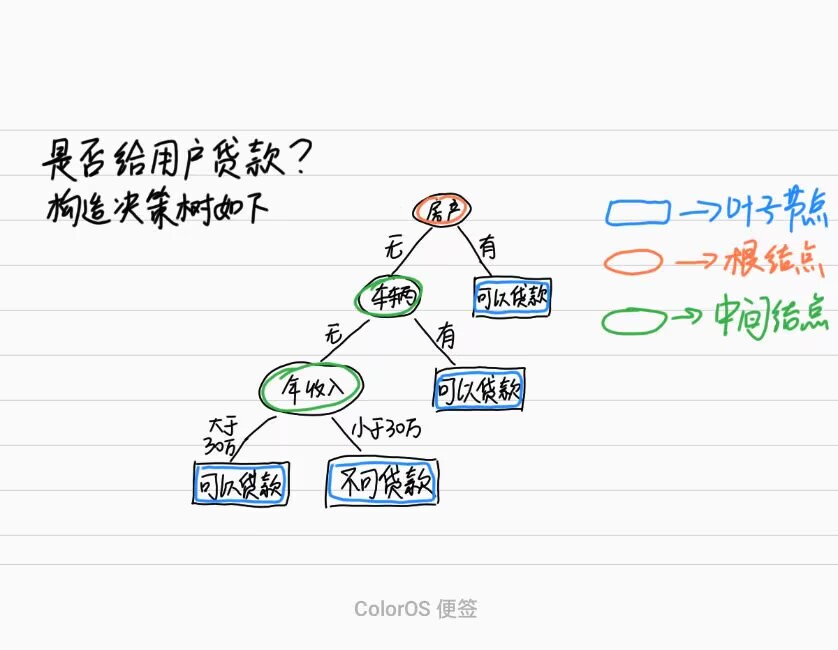
1.决策树结构
根节点:第一个节点
非叶子节点:中间节点
叶子节点:最终结果节点
2.如何构造决策树
根节点的选择,中间节点的选择,叶子节点的选择,节点如何分裂,分裂标准的依据?
决策树分类标准有三种:
ID3算法,C4.5算法,CART决策树
二、ID3
衡量标准:熵值(表示随机变量不确定性的度量,或者说是物体内部的混乱程度)
熵值计算公式: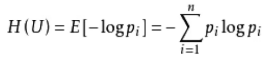
这里p是概率,然后累加
举一个例子:这里肉眼也是能看出B集合比较混乱

算法详细解释:
下面是一个数据,前四列为特征后一列为标签
天气,温度,湿度,风,是否出去玩
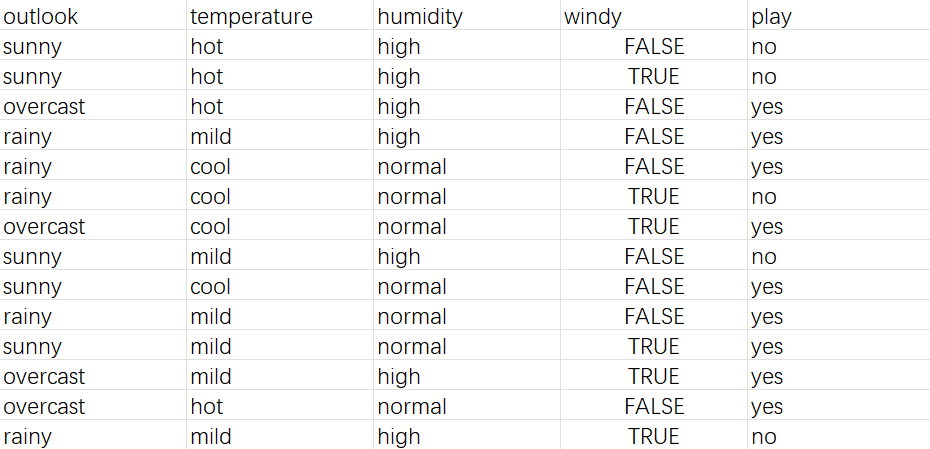
对该数据我们要构造一个决策树
选择根节点,中间节点,叶子节点及其分裂就要用到计算混乱程度,混乱程度越低,说明情况越简单,可以作为根节点
1)计算出标签也就是play的熵值:0.940
2)每一个特征的情况,情况次数,每次对应的标签值,然后计算出熵,求信息增益
信息增益:标签熵减去特征总熵

这里计算的outlook的信息增益就是outlook这个特征对结果的决策量,衡量这个特征是否重要,对结果影响有多大。
越大,说明对结果影响大,越适合做根节点。

其他特征也是这样
温度:0.940-0.911=0.029
湿度:0.940-0.789=0.151
风 : 0.940-0.892=0.048
0.247(outlook)>0.151(humidity)>0.048(windy)>0.029(temperature)
比较信息增益,outlook最大作为根节点目前我们的决策树为
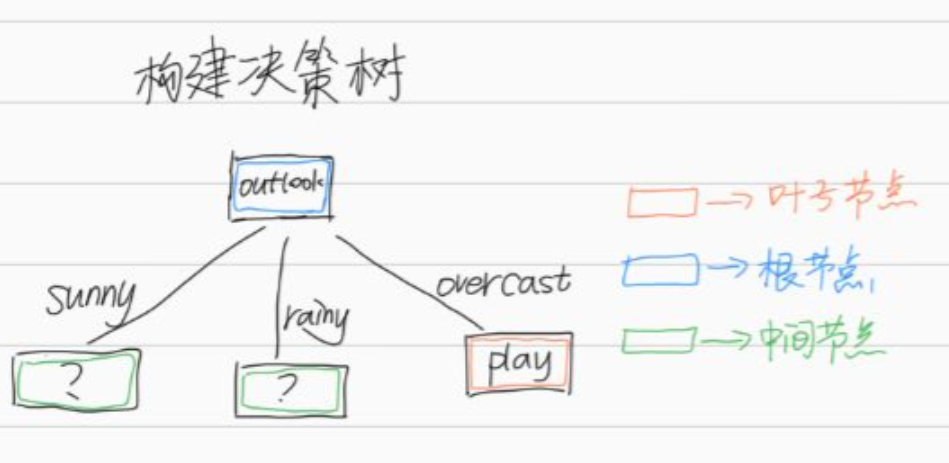
中间节点还不确定
注意这里我们不是求出各特征的信息增益后就按照从大到小安排当节点,就比如这里,sunny和rainy后写什么特征,这里依旧是需要重新进行计算,过程和原理与上面一样
3)找出对应情况的数据作为新表格算信息增益
这里把sunny和rainy的数据找出
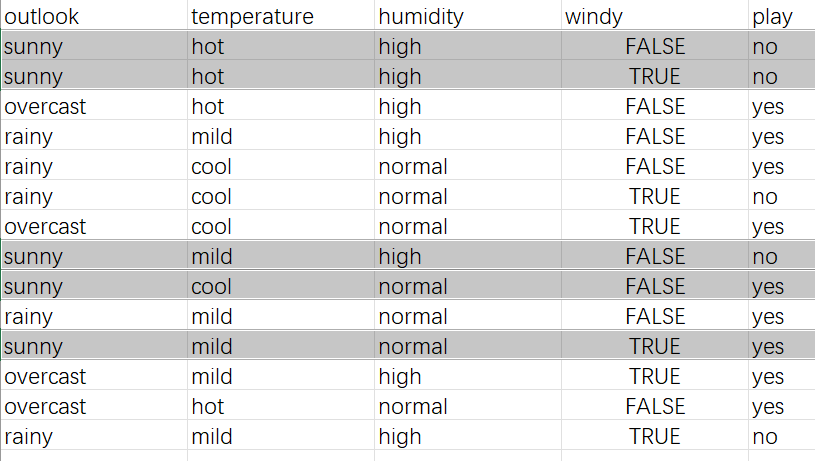
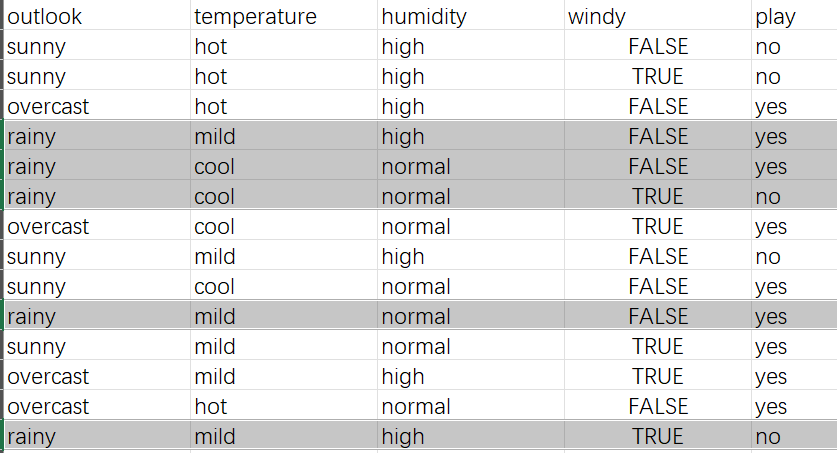
把阴影部分当作新表
以sunny中temperature为例

上面是temperature的总熵,这里我们还需要注意一点就是,标签熵是多少,不要用之前总表算出的标签熵,我们把黑色部分组成新表,所以标签熵也要重新算,这里计算得出:0.971
依次算出其他特征,最后sunny处是temperature
其他不做计算
三、C4.5算法
解决稀疏向量的问题,例如编号


意思就是C4.5算法是在ID3算法基础上,也是要算信息增益,但是C4.5算法要除以一个自身熵值得到信息增益比
计算信息增益的时候我们求出的特征总熵是条件熵,这里我们要除以的自身熵值是特征原始熵,是不一样的。也就是说不需要考虑标签值,只把该特征的值进行计算,和本文一开始拿集合A和集合B举例那样计算。
outlook信息增益为0.247,自身熵:1.577
信息增益率:0.247/1.577=0.1566
四、基尼指数
以下是贷款情况数据
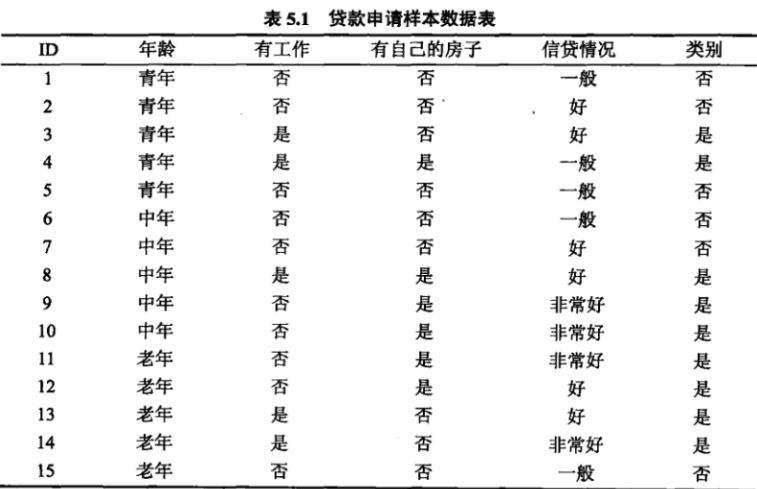
计算基尼系数公式:



现在在数据表下,特征年龄下

这里知道大致计算流程就可以
五、代码构建决策树
1.构建和参数介绍


参数1,默认情况下是基尼系数
参数2,最优还是随机选择特征做根节点?默认情况下是best
参数3,特征数量很大才会启用
参数4,也就是树的层数,用来限制层数


这些参数不是很重要,了解就行
2。决策树剪枝
防止过拟合,剪枝分为两种,预剪枝和后剪枝
特征中经过计算没有合适的,需要一直进行判断,导致决策树层数很多,说白了不是分类了,到最后几乎每一条数据就是一类了,然后我们输入数据进行分类,根本没有合适的类别给这个数据,这个就是过拟合,之前学习逻辑回归时也说过过拟合,就是模型分的过于细而导致的。
对于决策树我们就会限制它的层数,这样就不会出现到最后几乎很少的数据甚至一条数据是一个类别。剪掉多余的层数,该层数下的数据就会归为一类。
预剪枝就是边建立决策树边剪。后剪枝就是等决策树建好后再进行剪枝,虽然准确率高但是很慢,所以一般选择预剪枝。

3.电信客户流失数据(决策树实现分类)
数据:
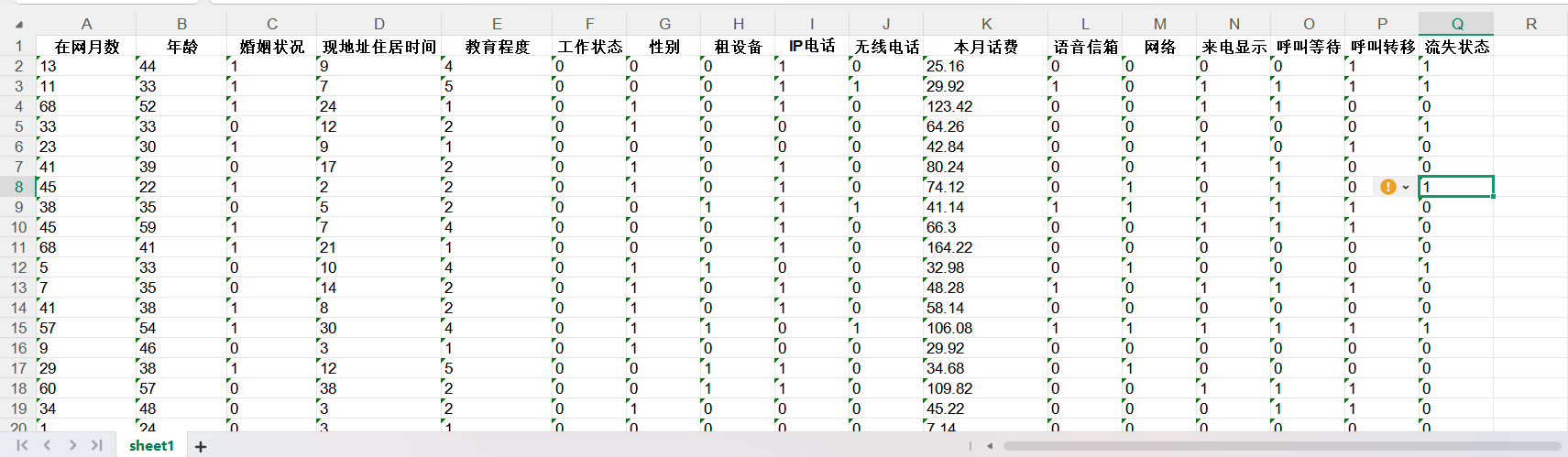
代码:
python
import numpy as np
import pandas as pd
def cm_plot(y, yp):#混淆矩阵绘制
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
cm = confusion_matrix(y, yp)
plt.matshow(cm, cmap=plt.cm.Blues)
plt.colorbar()
for x in range(len(cm)):
for y in range(len(cm)):
plt.annotate(cm[x, y], xy=(y, x), horizontalalignment='center',
verticalalignment = 'center')
plt.ylabel('True label')
plt.xlabel('Predicted label')
return plt
#导入数据
alldata=pd.read_excel("D:\learn\代码所用文本\电信客户流失数据.xlsx")
data=alldata.iloc[:,:-1]
result=alldata.iloc[:,-1]
#划分数据
from sklearn.model_selection import train_test_split
data_train,data_test,result_train,result_test=train_test_split(data,result, test_size=0.2,random_state=40)
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_val_score
#选出最优层数
scores=[]
depths=[4,5,6,7,8,9,10]
for i in depths:
tree=DecisionTreeClassifier(criterion='gini',max_depth=i,random_state=44)
score=cross_val_score(tree,data,result,cv=5,scoring='recall')
score_nu=sum(score)/len(score)
scores.append(score_nu)
print(score_nu)
best_depths=depths[np.argmax(scores)]
print('最优depth:{}'.format(best_depths))
#建立模型
tree=DecisionTreeClassifier(criterion='gini',max_depth=best_depths,random_state=44)
tree.fit(data_train,result_train)
#自测和预测并画出混淆矩阵
from sklearn import metrics
train_pre=tree.predict(data_train)
print(metrics.classification_report(result_train,train_pre))
cm_plot(result_train,train_pre).show()
test_pre=tree.predict(data_test)
print(metrics.classification_report(result_test,test_pre))
cm_plot(result_test,test_pre).show()
tree.score(data_test,result_test)
#绘制决策树
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
fig,ax=plt.subplots(figsize=(32,32))
plot_tree(tree,filled=True,ax=ax)
plt.show()结果:

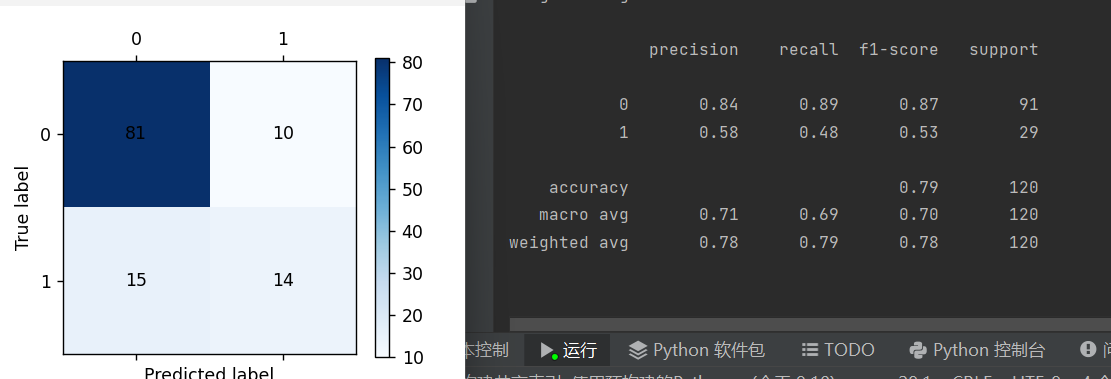
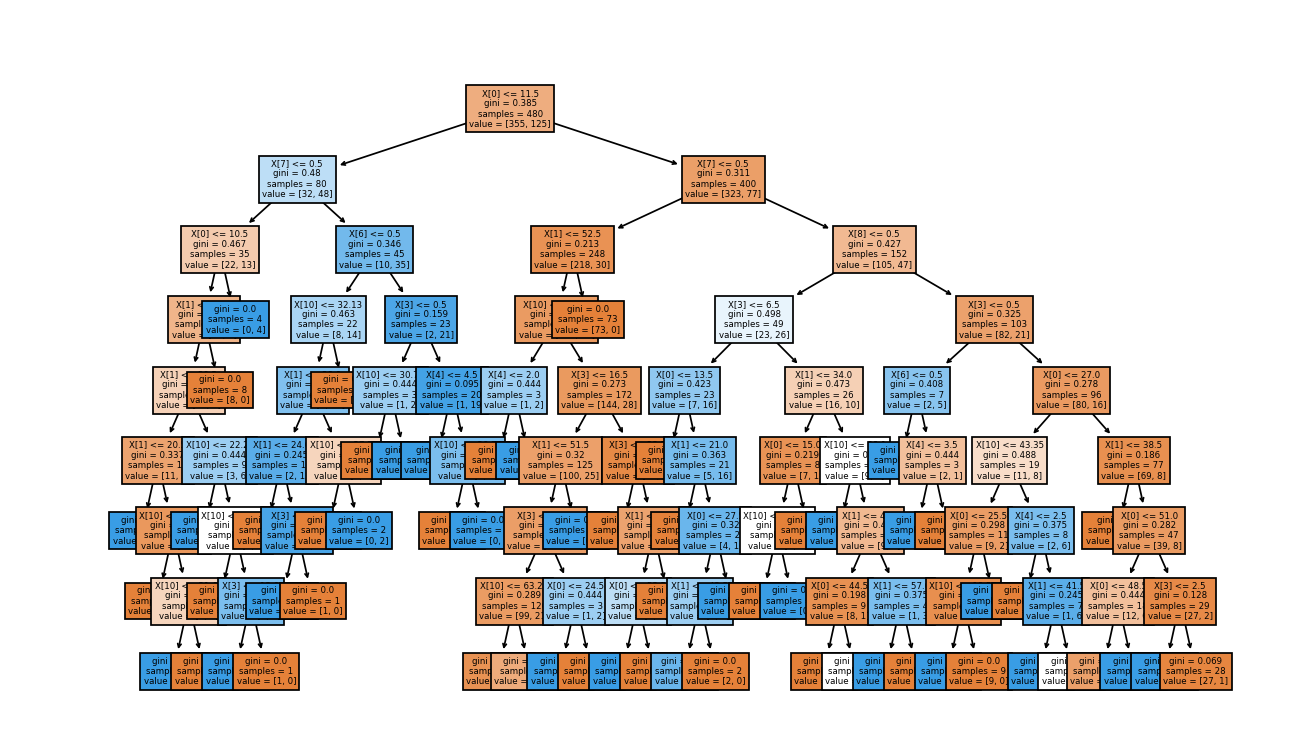
六、决策树之回归树模型(了解)
1.什么是回归树?
解决回归问题的决策树模型,特点是必须是二叉树
例子:
现在又一组数据

对其进行构造回归树,过程:
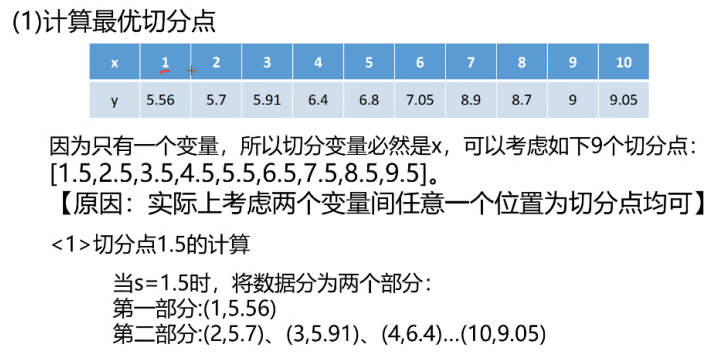
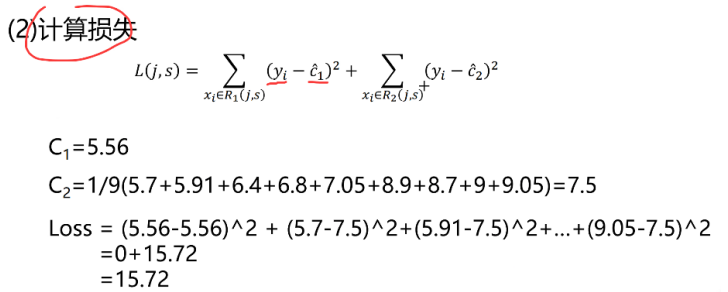
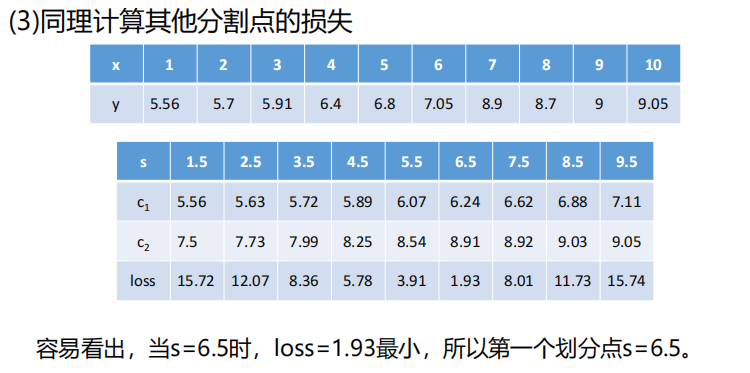
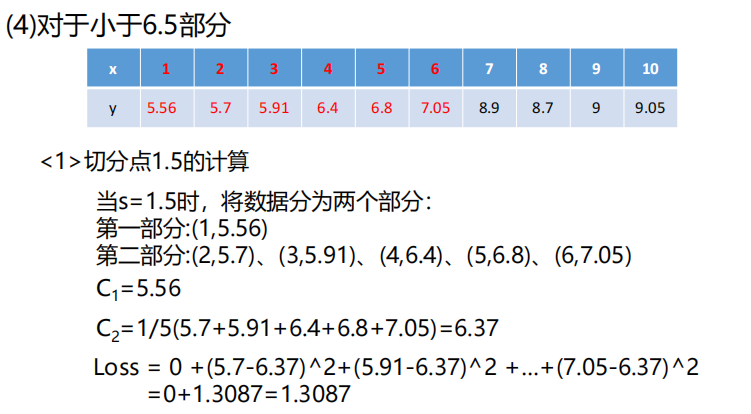
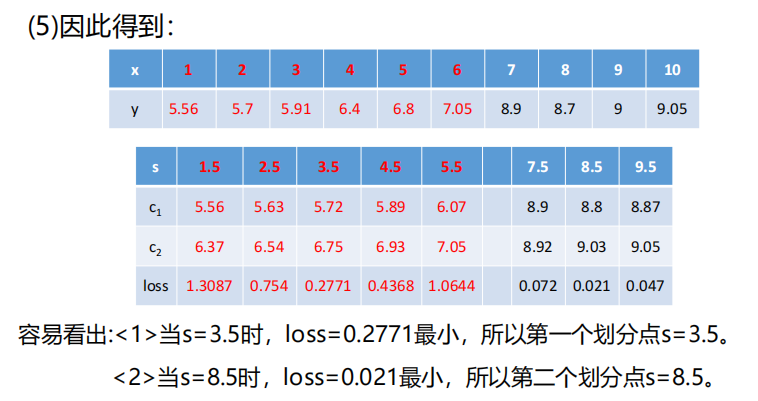
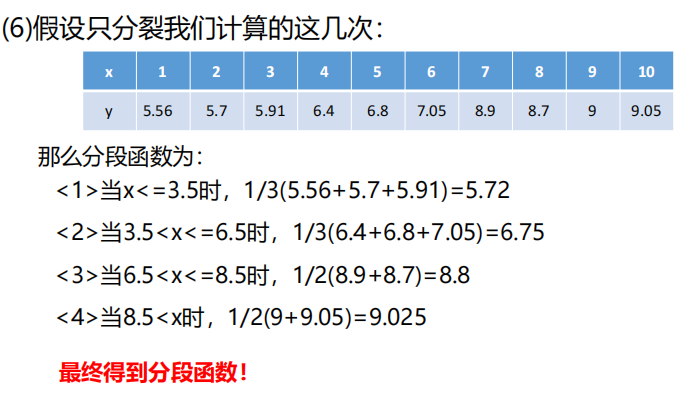

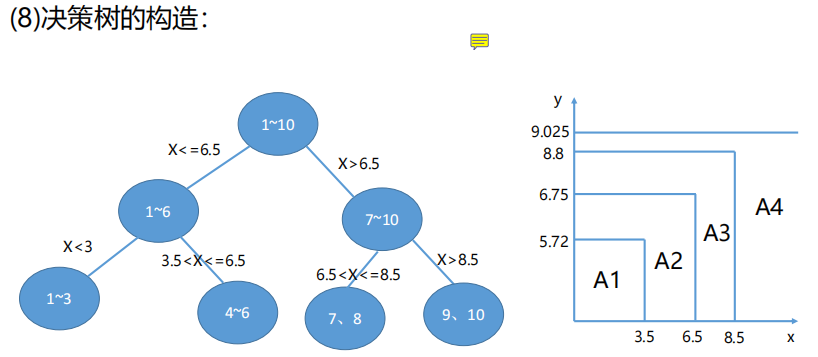
上面例子是只有一个变量x,如果是多个变量,如下

这里是x1进行了顺序排序,算出x1和y之间的最优切分点
然后对x2进行排序,注意这里的上下值也要跟着移动,然后算出x2与y之间的最优切分点
比较x1和x2的最优切分点,谁的损失小谁当根节点
2.参数和模型定义


回归树指标不高,仅作了解就行
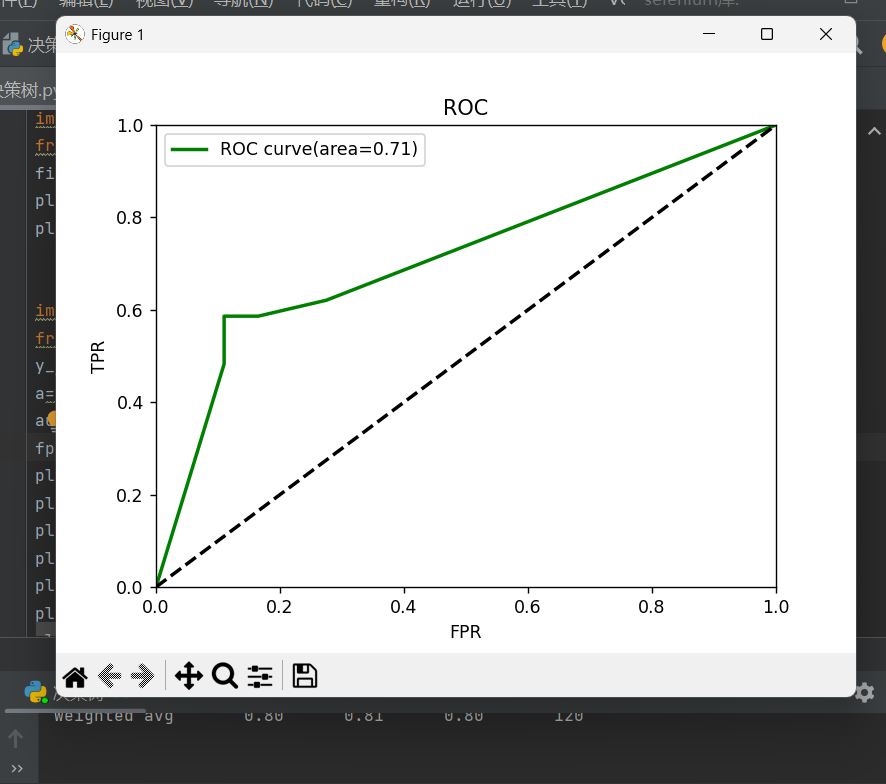
七、AUC性能测量

召回率为1是最好的,在纵轴上找到1,画平行于横轴的一条直线,FPR值为多少都无伤大雅,也找到1,画垂直于横轴的直线,这样两条直线和坐标轴形成的正方形,面积为1,是理想召回率,阴影部分就是我们模型的指标,如果阴影部分越大越接近一,说名指标越高
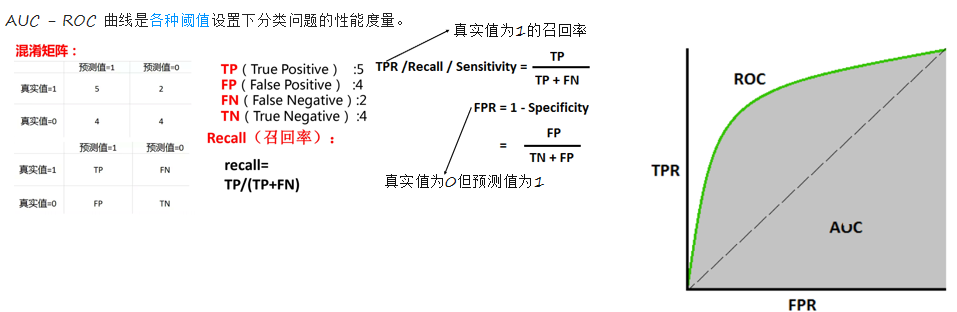

在上述代码处最后加上,就能绘制AUC-ROC曲线了
python
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve
y_pred_proba=tree.predict_proba(data_test)
a=y_pred_proba[:,1]
auc_result=metrics.roc_auc_score(result_test,a)
fpr,tpr,thresholds = roc_curve(result_test,a)
plt.figure()
plt.plot(fpr,tpr,color='green',lw=2,label='ROC curve(area=%0.2f)'% auc_result)
plt.plot([0,1],[0,1],color='black',lw=2,linestyle='--')
plt.xlim([0.0,1.0])
plt.ylim([0.0,1.0])
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.title('ROC')
plt.legend()
plt.show()