【算法基础篇】（三十五）图论基础之最小生成树：从原理到实战，彻底吃透 Prim 与 Kruskal 算法

---

目录

前言

[一、最小生成树的核心概念：先搞懂 "是什么"](#一、最小生成树的核心概念：先搞懂 “是什么”)

[1.1 生成树的定义](#1.1 生成树的定义)

[1.2 最小生成树的定义](#1.2 最小生成树的定义)

[1.3 最小生成树的性质](#1.3 最小生成树的性质)

[1.4 最小生成树的适用场景](#1.4 最小生成树的适用场景)

[二、Prim 算法："加点法" 构建最小生成树](#二、Prim 算法：“加点法” 构建最小生成树)

[2.1 Prim 算法的基本思想](#2.1 Prim 算法的基本思想)

[2.2 Prim 算法的图解过程](#2.2 Prim 算法的图解过程)

[2.3 Prim 算法的代码实现（邻接矩阵版）](#2.3 Prim 算法的代码实现（邻接矩阵版）)

代码说明：

[2.4 Prim 算法的代码实现（邻接表版）](#2.4 Prim 算法的代码实现（邻接表版）)

代码说明：

[2.5 Prim 算法的时间复杂度分析](#2.5 Prim 算法的时间复杂度分析)

[三、Kruskal 算法："加边法" 构建最小生成树](#三、Kruskal 算法：“加边法” 构建最小生成树)

[3.1 Kruskal 算法的基本思想](#3.1 Kruskal 算法的基本思想)

[3.2 Kruskal 算法的图解过程](#3.2 Kruskal 算法的图解过程)

[3.3 Kruskal 算法的代码实现（并查集 + 排序）](#3.3 Kruskal 算法的代码实现（并查集 + 排序）)

代码说明：

[3.4 Kruskal 算法的时间复杂度分析](#3.4 Kruskal 算法的时间复杂度分析)

[3.5 并查集的优化：路径压缩 + 按秩合并](#3.5 并查集的优化：路径压缩 + 按秩合并)

[四、Prim 算法与 Kruskal 算法的对比：该选哪一个？](#四、Prim 算法与 Kruskal 算法的对比：该选哪一个？)

选择建议：

五、经典例题实战：从模板到应用

[例题 1：买礼物（洛谷 P1194）](#例题 1：买礼物（洛谷 P1194）)

题目描述：

输入格式：

输出格式：

[示例输入 2：](#示例输入 2：)

[示例输出 2：](#示例输出 2：)

解法分析：

代码实现：

[例题 2：滑雪（洛谷 P2573）](#例题 2：滑雪（洛谷 P2573）)

题目描述：

输入格式：

输出格式：

示例输入：

示例输出：

解法分析：

代码实现：

总结

---

前言

在图论的世界里，有这样一个经典问题：给定一个连通图，如何找到一棵包含所有顶点、边权之和最小的树？这就是最小生成树（Minimum Spanning Tree，简称 MST）要解决的核心问题。小到城市间的公路规划、通信网络搭建，大到芯片布线、物流路径优化，最小生成树都发挥着至关重要的作用 ------ 它能在保证 "连通性" 的前提下，实现 "成本最小化"，堪称图论中的 "性价比之王"。

如果你是算法初学者，可能会对 "生成树""贪心策略" 这些概念感到困惑；如果你是有一定基础的开发者，或许想深入理解两种经典算法的底层逻辑与适用场景。本文将从最小生成树的基本概念出发，用通俗的语言拆解 Prim 算法和 Kruskal 算法的实现细节，结合大量图解和可直接运行的 C++ 代码，再通过 5 道经典例题巩固实战能力。无论你是学生还是职场人，相信都能从这篇文章中有所收获。下面就让问我们正式开始吧！

---

一、最小生成树的核心概念：先搞懂 "是什么"

在正式讲解算法之前，我们必须先理清几个关键概念 ------ 只有地基打牢了，后续的算法学习才能事半功倍。

1.1 生成树的定义

首先，我们回顾一下 "生成树" 的概念。对于一个连通无向图G=(V,E)：

• 生成树是 G 的一个子图，包含 G 中所有的顶点（即 V'=V）；
• 这个子图是一棵树（无回路、连通），因此边数恰好为 n-1（n 为顶点个数）；
• 生成树具有**"极小连通性"**：去掉任意一条边，树就会变成非连通图；增加任意一条边，就会形成回路。

一个连通图的生成树可能有多个。例如，一个有 4 个顶点、5 条边的图，可能存在多棵不同的生成树，每棵树都包含 3 条边且连接所有顶点。

1.2 最小生成树的定义

最小生成树，就是所有生成树中边权之和最小的那一棵。如下图所示：

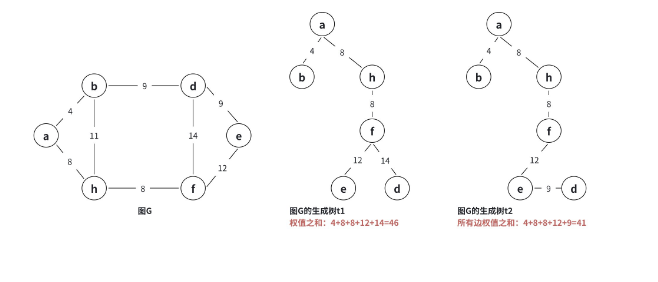
1.3 最小生成树的性质

最小生成树有两个非常重要的性质，也是后续算法正确性的基础：

1. 切割性质：设 S 是顶点集 V 的一个非空子集，若边 (u,v) 是跨越 S 和 V-S 的所有边中权值最小的，则 (u,v) 一定在某棵最小生成树中；
2. 回路性质：若边 (u,v) 是某回路中权值最大的边，则 (u,v) 一定不在任何一棵最小生成树中。

这两个性质看似抽象，其实很容易理解：切割性质告诉我们**"最小的跨界边必须选"** ，回路性质告诉我们**"最大的回路边必须丢"**------ 这正是贪心策略在最小生成树中的体现。

1.4 最小生成树的适用场景

最小生成树的核心是 "连通所有点，成本最小"，因此它的应用场景非常广泛：

• 通信网络搭建：用最少的光纤连接所有城市，保证数据互通；
• 公路建设规划：在多个城镇间修建公路，使总造价最低；
• 芯片布线：在芯片上连接多个元件，使导线总长度最短；
• 物流配送：规划仓库与多个配送点的路线，使运输成本最低。

了解了这些基本概念后，我们就可以正式进入算法的学习了。

二、Prim 算法："加点法" 构建最小生成树

Prim 算法是最小生成树的经典算法之一，由计算机科学家 Robert C. Prim 于 1957 年提出。它的核心思路是 "从一个顶点出发，逐步将距离当前树最近的顶点加入树中，直到所有顶点都被加入"------ 简单来说，就是 "先有一个点，慢慢扩建成一棵树"。

2.1 Prim 算法的基本思想

Prim 算法的本质是贪心策略，每一步都选择 "当前最优" 的决策，最终得到全局最优解。具体步骤如下：

1. 初始化 ：选择任意一个顶点作为起始点（通常选顶点 1），将其加入生成树中；同时，维护一个 dist 数组，**dist [i]**表示顶点 i 到当前生成树的最短距离（初始时，起始点的 dist 为 0，其他顶点的 dist 为无穷大）；
2. 选最近点：在所有未加入生成树的顶点中，找到 dist 值最小的顶点 u，将 u 加入生成树；
3. 更新距离 ：对于顶点 u 的所有邻接顶点 v，若 v 未加入生成树，且边 (u,v) 的权值小于 dist [v]，则更新 dist [v] = 边 (u,v) 的权值；
4. 重复步骤 2-3：直到所有顶点都被加入生成树（共执行 n 次，n 为顶点数）。

举个通俗的例子：把生成树想象成一个 "朋友圈"，起始点是你自己。每次都邀请当前和你关系最好（距离最近）的人加入朋友圈，然后通过这个人，看看他的朋友中有没有和你关系更近的，更新关系后再邀请下一个人，直到所有人都加入朋友圈。

2.2 Prim 算法的图解过程

为了让大家更直观地理解，我们用一个具体的图来演示 Prim 算法的执行过程：

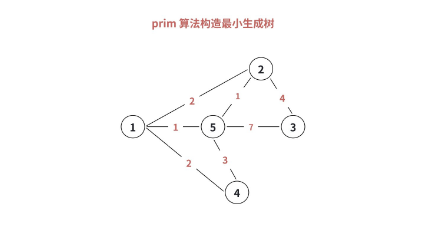
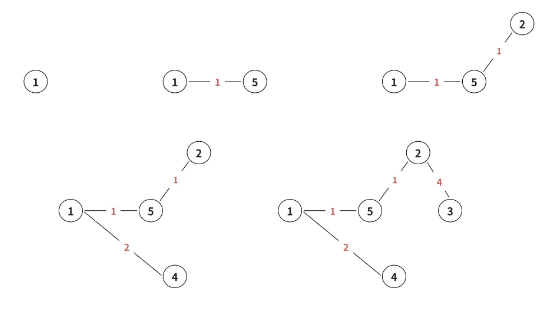
2.3 Prim 算法的代码实现（邻接矩阵版）

Prim 算法的实现有两种常见方式：邻接矩阵和邻接表。邻接矩阵适用于稠密图 （边数多，接近 n²），代码简洁直观；邻接表适用于稀疏图（边数少，远小于 n²），空间效率更高。

首先给出邻接矩阵版的实现，适用于 n 较小的场景（比如 n≤5000）：

#include <iostream>
#include <cstring>
using namespace std;

const int N = 5010, INF = 0x3f3f3f3f;

int n, m;
int edges[N][N];  // 邻接矩阵存储图，edges[i][j]表示i到j的边权，无穷大表示无边
int dist[N];      // dist[i]表示顶点i到当前生成树的最短距离
bool st[N];       // st[i]标记顶点i是否已加入生成树

int prim() {
    // 初始化dist数组为无穷大
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;  // 起始点选1，距离为0
    int ret = 0;  // 存储最小生成树的权值和

    // 共需要加入n个顶点，循环n次
    for (int i = 1; i <= n; i++) {
        // 步骤1：找到未加入树且dist最小的顶点t
        int t = 0;
        for (int j = 1; j <= n; j++) {
            if (!st[j] && dist[j] < dist[t]) {
                t = j;
            }
        }

        // 如果dist[t]仍是无穷大，说明图不连通，无最小生成树
        if (dist[t] == INF) return INF;

        // 将t加入生成树，累加权值
        st[t] = true;
        ret += dist[t];

        // 步骤2：更新t的邻接顶点到生成树的距离
        for (int j = 1; j <= n; j++) {
            if (!st[j] && edges[t][j] < dist[j]) {
                dist[j] = edges[t][j];
            }
        }
    }

    return ret;
}

int main() {
    cin >> n >> m;

    // 初始化邻接矩阵为无穷大
    memset(edges, 0x3f, sizeof edges);
    // 自环边权值为0（实际中无意义，避免干扰）
    for (int i = 1; i <= n; i++) edges[i][i] = 0;

    // 读入m条边（无向图，双向存储）
    for (int i = 1; i <= m; i++) {
        int x, y, z;
        cin >> x >> y >> z;
        // 处理重边：保留权值最小的边
        edges[x][y] = edges[y][x] = min(edges[x][y], z);
    }

    int res = prim();
    if (res == INF) {
        cout << "orz" << endl;  // 图不连通
    } else {
        cout << res << endl;    // 输出最小生成树的权值和
    }

    return 0;
}

代码说明：

1. 数据结构 ：

   • edges[N][N]：邻接矩阵，存储图的边权，初始值为无穷大（0x3f3f3f3f），表示无边；
   • dist[N]：存储每个顶点到当前生成树的最短距离；
   • st[N]：标记顶点是否已加入生成树；

2. 核心逻辑 ：

   • 外层循环 n 次，每次加入一个顶点；
   • 内层第一个循环找 "未加入树且距离最近" 的顶点 t；
   • 检查图是否连通（dist [t] == INF 则不连通）；
   • 累加权值后，更新 t 的邻接顶点的距离；

3. 处理重边：无向图中可能存在多条连接同一对顶点的边，我们只保留权值最小的那条，避免影响结果。

2.4 Prim 算法的代码实现（邻接表版）

当 n 较大（比如 n=1e5）时，邻接矩阵的空间复杂度 O (n²) 会超出内存限制，此时需要用邻接表存储图。邻接表的空间复杂度为 O (m)（m 为边数），适用于稀疏图。

邻接表版的实现如下：

#include <iostream>
#include <vector>
#include <cstring>
using namespace std;

typedef pair<int, int> PII;  // first存储邻接顶点，second存储边权
const int N = 5010, INF = 0x3f3f3f3f;

int n, m;
vector<PII> edges[N];  // 邻接表存储图
int dist[N];
bool st[N];

int prim() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    int ret = 0;

    for (int i = 1; i <= n; i++) {
        // 找到未加入树且dist最小的顶点t
        int t = 0;
        for (int j = 1; j <= n; j++) {
            if (!st[j] && dist[j] < dist[t]) {
                t = j;
            }
        }

        if (dist[t] == INF) return INF;

        st[t] = true;
        ret += dist[t];

        // 更新t的邻接顶点的距离（邻接表遍历）
        for (auto& p : edges[t]) {
            int v = p.first;  // 邻接顶点
            int w = p.second; // 边权
            if (!st[v] && w < dist[v]) {
                dist[v] = w;
            }
        }
    }

    return ret;
}

int main() {
    cin >> n >> m;

    for (int i = 1; i <= m; i++) {
        int x, y, z;
        cin >> x >> y >> z;
        // 无向图，双向添加边
        edges[x].push_back({y, z});
        edges[y].push_back({x, z});
    }

    int res = prim();
    if (res == INF) {
        cout << "orz" << endl;
    } else {
        cout << res << endl;
    }

    return 0;
}

代码说明：

1. 用**vector<PII>**存储邻接表，每个元素是(邻接顶点, 边权)的键值对；
2. 遍历邻接顶点时，直接迭代edges[t]，效率比邻接矩阵更高；
3. 重边的处理：由于邻接表会存储所有边，但在更新**dist[v]**时，会自动选择最小的边权，因此无需额外处理重边。

2.5 Prim 算法的时间复杂度分析

• 邻接矩阵版：外层循环 n 次，内层两个循环各 n 次，总时间复杂度为 O (n²)；
• 邻接表版：外层循环 n 次，找最小顶点的循环 n 次，更新邻接顶点的循环总次数为 O (m)（每个边被遍历两次），总时间复杂度为 O (n² + m)。

当图是稠密图 （m≈n²）时，两种版本的时间复杂度相近；当图是稀疏图（m≈n）时，邻接表版的时间复杂度接近 O (n²)，但空间效率更高。

如果想进一步优化时间复杂度，可以使用 "堆优化" 版的 Prim 算法，将 "找最小顶点" 的时间复杂度从 O (n) 降到 O (log n)，整体时间复杂度优化为 O (m log n)，适用于更大规模的稀疏图。不过堆优化版的代码稍复杂，初学者可以先掌握基础版本，后续再深入学习。

三、Kruskal 算法："加边法" 构建最小生成树

Kruskal 算法是另一种经典的最小生成树算法，由 Joseph Kruskal 于 1956 年提出。它的核心思路与 Prim 算法完全不同：先将所有边按权值排序，然后依次选择权值最小的边，若该边的两个顶点不在同一连通分量中，则将其加入生成树，直到所有顶点都连通------ 简单来说，就是 "先有所有边，慢慢选边拼成树"。

3.1 Kruskal 算法的基本思想

Kruskal 算法同样基于贪心策略，但它的贪心体现在 "选边" 上：每次选权值最小的边，同时保证选的边不会形成回路。为了判断两个顶点是否在同一连通分量中，需要用到并查集（Union-Find） 这一数据结构 ------ 并查集能高效地处理 "合并集合" 和 "查询集合根节点" 的操作，是 Kruskal 算法的核心支撑。

具体步骤如下：

1. 初始化：将所有边按权值从小到大排序；初始化并查集，每个顶点各自成为一个独立的集合；
2. 选最小边：依次从排序后的边中选择权值最小的边 (u, v)；
3. 判断连通性：用并查集查询 u 和 v 的根节点。若根节点不同（说明 u 和 v 不在同一连通分量中），则将该边加入生成树，并合并 u 和 v 所在的集合；若根节点相同（说明加入该边会形成回路），则跳过该边；
4. 重复步骤 2-3：直到生成树中包含 n-1 条边（所有顶点连通）或所有边都处理完毕。

举个通俗的例子：把所有边想象成 "候选公路"，按造价从低到高排序。每次选造价最低的公路，只要它能连接两个之前不连通的城市，就修建这条公路；如果它连接的是已经连通的城市，就放弃这条公路，直到所有城市都连通。

3.2 Kruskal 算法的图解过程

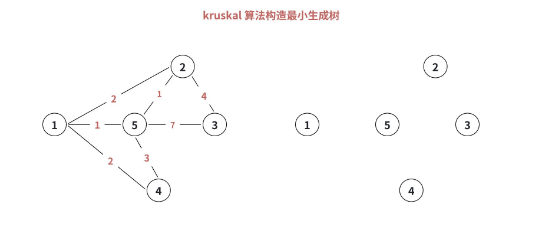
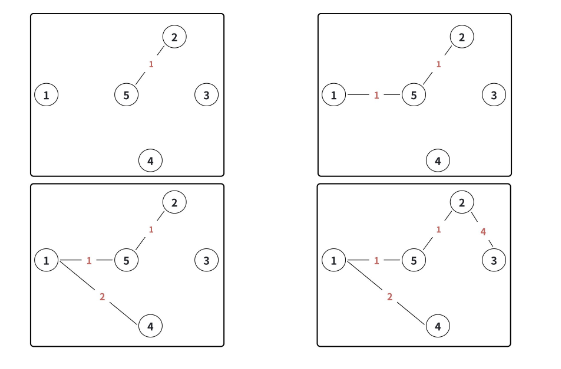
3.3 Kruskal 算法的代码实现（并查集 + 排序）

Kruskal 算法的代码核心是**"边排序"** 和 "并查集操作"，实现如下：

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 5010, M = 2e5 + 10, INF = 0x3f3f3f3f;

int n, m;
// 存储边：x和y是顶点，z是边权
struct Edge {
    int x, y, z;
} edges[M];

// 并查集数组：parent[i]表示顶点i的父节点
int parent[N];

// 比较函数：按边权从小到大排序
bool cmp(Edge a, Edge b) {
    return a.z < b.z;
}

// 并查集查询操作（路径压缩）
int find(int x) {
    if (parent[x] != x) {
        parent[x] = find(parent[x]);
    }
    return parent[x];
}

int kruskal() {
    // 初始化并查集
    for (int i = 1; i <= n; i++) {
        parent[i] = i;
    }

    // 对边按权值排序
    sort(edges + 1, edges + 1 + m, cmp);

    int cnt = 0;  // 生成树中已选的边数
    int ret = 0;  // 最小生成树的权值和

    for (int i = 1; i <= m; i++) {
        int x = edges[i].x;
        int y = edges[i].y;
        int z = edges[i].z;

        // 查询x和y的根节点
        int fx = find(x);
        int fy = find(y);

        // 若根节点不同，说明不连通，加入该边
        if (fx != fy) {
            parent[fx] = fy;  // 合并集合
            cnt++;
            ret += z;

            // 当边数达到n-1时，说明所有顶点已连通，直接返回
            if (cnt == n - 1) {
                break;
            }
        }
    }

    // 若边数不足n-1，说明图不连通
    return cnt == n - 1 ? ret : INF;
}

int main() {
    cin >> n >> m;

    // 读入m条边
    for (int i = 1; i <= m; i++) {
        cin >> edges[i].x >> edges[i].y >> edges[i].z;
    }

    int res = kruskal();
    if (res == INF) {
        cout << "orz" << endl;
    } else {
        cout << res << endl;
    }

    return 0;
}

代码说明：

1. 数据结构 ：

   • Edge结构体：存储每条边的两个顶点和权值；
   • parent[N]：并查集的父节点数组；

2. 核心逻辑 ：

   • 并查集初始化：每个顶点的父节点是自己；
   • 边排序：按权值从小到大排序，保证每次选最小边；
   • 并查集查询：用路径压缩优化，提高查询效率；
   • 合并集合：若两个顶点不连通，合并它们的集合，并累加边权；

3. 终止条件：当生成树的边数达到 n-1 时，直接返回结果，无需继续处理后续边，提高效率。

3.4 Kruskal 算法的时间复杂度分析

Kruskal 算法的时间复杂度主要由两部分构成：

1. 边排序：时间复杂度为 O (m log m)（m 为边数）；
2. 并查集操作：每次查询和合并的时间复杂度接近 O (1)（路径压缩和按秩合并优化后），总共有 m 次操作，时间复杂度为 O (m α(n))（α 是阿克曼函数的反函数，增长极慢，可视为常数）；

因此，Kruskal 算法的总时间复杂度为 O (m log m)，这使得它非常适合稀疏图（m 较小）------ 当 m 远小于 n² 时，Kruskal 算法的效率远高于 Prim 算法的 O (n²) 版本。

3.5 并查集的优化：路径压缩 + 按秩合并

在上面的代码中，我们只使用了 "路径压缩" 优化并查集的查询操作。为了进一步提高效率，还可以加入 "按秩合并" 优化 ------ 合并两个集合时，将秩（树的高度）较小的集合合并到秩较大的集合中，避免树的高度过高，从而优化查询效率。

优化后的并查集实现如下：

// 并查集数组：parent[i]表示父节点，rank[i]表示树的秩（高度）
int parent[N], rank[N];

// 初始化并查集
void init() {
    for (int i = 1; i <= n; i++) {
        parent[i] = i;
        rank[i] = 1;  // 初始时每个树的秩为1
    }
}

// 查询操作（路径压缩）
int find(int x) {
    if (parent[x] != x) {
        parent[x] = find(parent[x]);
    }
    return parent[x];
}

// 合并操作（按秩合并）
void unite(int x, int y) {
    int fx = find(x);
    int fy = find(y);
    if (fx == fy) return;

    // 将秩小的树合并到秩大的树中
    if (rank[fx] < rank[fy]) {
        parent[fx] = fy;
    } else {
        parent[fy] = fx;
        // 若秩相等，合并后秩+1
        if (rank[fx] == rank[fy]) {
            rank[fx]++;
        }
    }
}

将 Kruskal 算法中的并查集部分替换为上述代码，可进一步提高算法效率，尤其是在顶点数较多的场景下。

四、Prim 算法与 Kruskal 算法的对比：该选哪一个？

通过前面的学习，我们已经掌握了两种最小生成树算法的实现。那么在实际应用中，该如何选择合适的算法呢？下面从多个维度进行对比：

对比维度	Prim 算法	Kruskal 算法
核心思想	加点法：从顶点出发，逐步扩展生成树	加边法：从边出发，逐步选择有效边
数据结构依赖	邻接矩阵 / 邻接表	并查集 + 边排序
时间复杂度	基础版 O (n²)，堆优化版 O (m log n)	O(m log m)
空间复杂度	邻接矩阵 O (n²)，邻接表 O (n+m)	O (m)（存储边）+ O (n)（并查集）
适用场景	稠密图（m≈n²）	稀疏图（m≈n）
处理带权图	支持非负权边	支持非负权边
处理图不连通	可检测（返回 INF）	可检测（边数不足 n-1）

选择建议：

1. 如果是稠密图（比如 n=1000，m=1e6），优先选择 Prim 算法的邻接矩阵版，代码简洁，效率稳定；
2. 如果是稀疏图（比如 n=1e5，m=1e5），优先选择 Kruskal 算法，时间复杂度 O (m log m)，空间效率更高；
3. 如果顶点数较少（n≤1000），两种算法都可以，可根据个人习惯选择；
4. 如果需要处理更大规模的稀疏图，可选择堆优化版的 Prim 算法或优化后的 Kruskal 算法。

五、经典例题实战：从模板到应用

理论学习之后，必须通过实战巩固。下面为大家精选了两道洛谷上的经典例题，涵盖模板题、应用场景题、变形题，帮助大家灵活运用两种算法。

例题 1：买礼物（洛谷 P1194）

题目链接：https://www.luogu.com.cn/problem/P1194

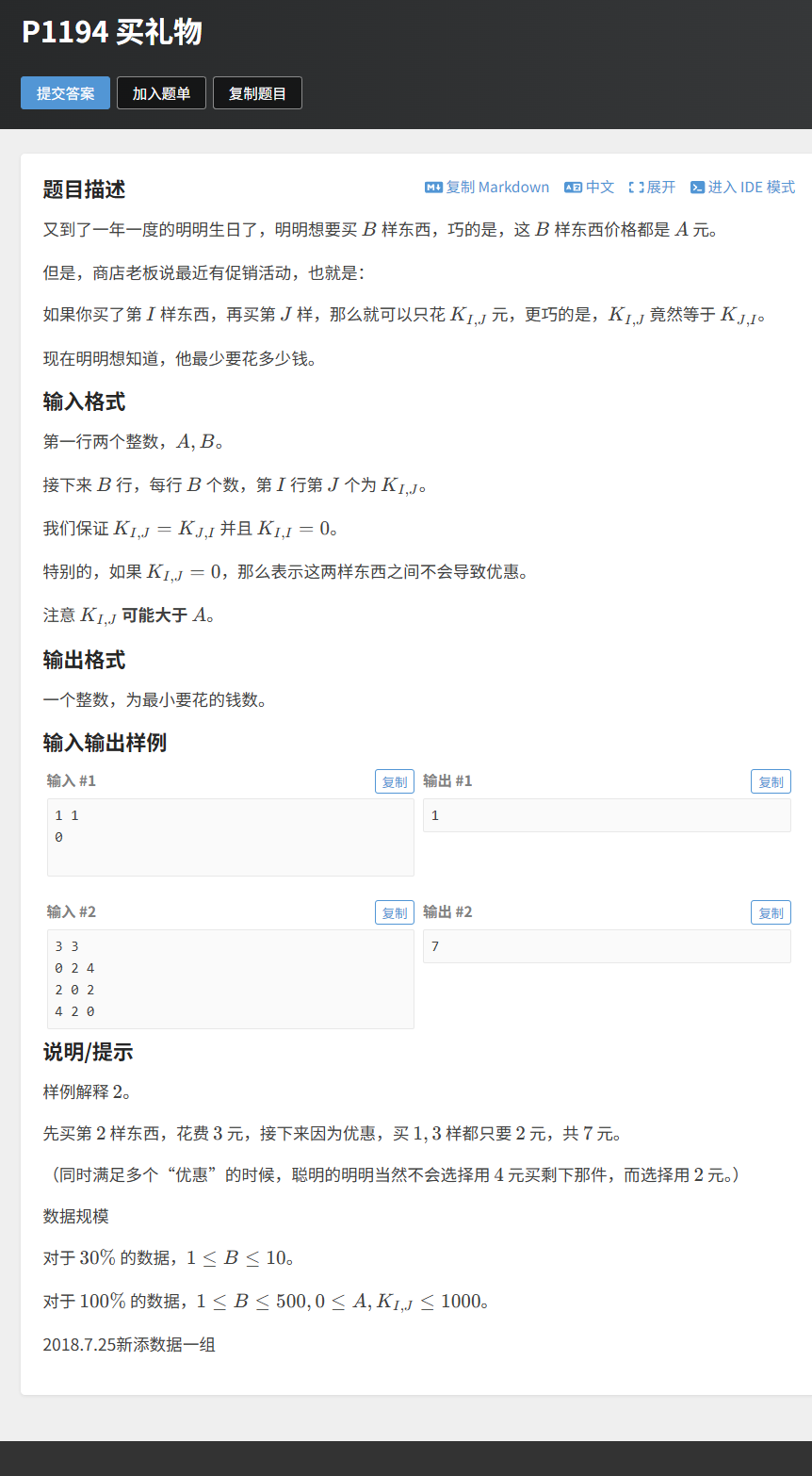
题目描述：

明明想要买 B 样东西，每样东西价格都是 A 元。商店有促销活动：如果买了第 I 样东西，再买第 J 样，那么就可以只花 K_{I,J} 元（K_{I,J}=K_{J,I}）。若 K_{I,J}=0，则无优惠。求明明最少要花多少钱。

输入格式：

第一行两个整数 A、B。接下来 B 行，每行 B 个数，第 I 行第 J 个为 K_{I,J}。

输出格式：

一个整数，为最小要花的钱数。

示例输入 2：

3 3
0 2 4
2 0 2
4 2 0

示例输出 2：

7

解法分析：

这道题的关键是将问题转化为最小生成树问题：

• 每个礼物看作一个顶点（共 B 个顶点）；
• 优惠活动 K_{I,J} 看作连接顶点 I 和 J 的边，边权为 K_{I,J}；
• 若不使用优惠，买第 I 样东西的成本是 A 元，相当于每个顶点有一条 "自环边"（或连接到一个虚拟顶点的边），边权为 A；

最终，问题转化为：选择一些边，使得所有顶点都被覆盖（即买所有礼物），且边权之和最小。这里有两种选择：

1. 直接买某样礼物，花费 A 元（相当于选 "自环边"）；
2. 先买另一样礼物，再用优惠买该礼物，花费 K_{I,J} 元（相当于选连接 I 和 J 的边）；

因此，我们可以构建一个包含 B 个顶点的图，边包括所有有效的 K_{I,J}（K_{I,J}≠0 且 K_{I,J}<A），然后求最小生成树。生成树的边权之和，加上未被覆盖的顶点的 A 元（实际上生成树包含所有顶点，因此无需额外加），就是最小总花费。

代码实现：

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 500 * 500 + 10;

int A, B;
struct Edge {
    int x, y, z;
} edges[N];
int parent[N];
int pos = 0;  // 边的计数器

bool cmp(Edge a, Edge b) {
    return a.z < b.z;
}

int find(int x) {
    if (parent[x] != x) parent[x] = find(parent[x]);
    return parent[x];
}

int main() {
    cin >> A >> B;

    // 读入优惠边（K_ij≠0且K_ij<A，且i<j避免重复）
    for (int i = 1; i <= B; i++) {
        for (int j = 1; j <= B; j++) {
            int k;
            cin >> k;
            if (i >= j || k == 0 || k >= A) continue;
            edges[++pos] = {i, j, k};
        }
    }

    // 初始化并查集
    for (int i = 1; i <= B; i++) parent[i] = i;

    // Kruskal算法选边
    sort(edges + 1, edges + 1 + pos, cmp);
    int cnt = 0, res = 0;
    for (int i = 1; i <= pos; i++) {
        int x = edges[i].x, y = edges[i].y, z = edges[i].z;
        int fx = find(x), fy = find(y);
        if (fx != fy) {
            parent[fx] = fy;
            cnt++;
            res += z;
        }
    }

    // 总花费 = 生成树边权和 + 未被优惠覆盖的顶点数 * A
    // 未被优惠覆盖的顶点数 = B - cnt（生成树有cnt条边，覆盖cnt+1个顶点？不，生成树有B个顶点，cnt=B-1时覆盖所有）
    // 实际上，每个顶点要么通过优惠边连接（计入res），要么直接购买（花费A），因此总花费=res + (B - cnt) * A
    cout << res + (B - cnt) * A << endl;

    return 0;
}

例题 2：滑雪（洛谷 P2573）

题目链接：https://www.luogu.com.cn/problem/P2573

题目描述：

雪山有 n 个景点（顶点），m 条轨道（边），每个景点有高度 h_i。可以从景点 i 滑到 j 当且仅当 h_i ≥ h_j。可以使用时间胶囊回溯到之前的景点。求最多能到达多少个景点，以及此时的最短滑行距离总和。

输入格式：

第一行 n、m；第二行 n 个整数 h_i；接下来 m 行 u、v、k，表示景点 u 和 v 之间有一条长度为 k 的轨道。

输出格式：

最多能到达的景点数和最短滑行距离总和。

示例输入：

3 3
3 2 1
1 2 1
2 3 1
1 3 10

示例输出：

3 2

解法分析：

这道题是最小生成树的变形，需要结合 DFS 和 Kruskal 算法：

1. 最多能到达的景点数：从起点 1 出发，通过 DFS/BFS 遍历所有可达的景点（h_i ≥ h_j），统计个数；
2. 最短滑行距离总和：由于可以回溯，相当于需要选择一些边，将所有可达的景点连接起来，且边权之和最小（即最小生成树）。但由于滑行方向限制（h_i ≥ h_j），排序时需优先选择高度高的顶点的边，确保能向下滑行。

代码实现：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
using namespace std;

typedef long long LL;
typedef pair<int, int> PII;
const int N = 1e5 + 10, M = 2e6 + 10;

int n, m;
int h[N];  // 每个景点的高度
vector<PII> edges[N];  // 存储图
bool st[N];  // 标记是否已遍历（DFS用）
int cnt = 0;  // 最多能到达的景点数

// 存储用于Kruskal的边
struct Edge {
    int x, y, z;
} e[M];
int pos = 0;  // 边的计数器
int parent[N];

// DFS遍历所有可达的景点
void dfs(int u) {
    cnt++;
    st[u] = true;
    for (auto& p : edges[u]) {
        int v = p.first, k = p.second;
        // 记录边（用于后续Kruskal）
        e[++pos] = {u, v, k};
        if (!st[v] && h[u] >= h[v]) {
            dfs(v);
        }
    }
}

// 边排序：优先按邻接顶点的高度降序，再按边权升序
bool cmp(Edge a, Edge b) {
    if (h[a.y] != h[b.y]) return h[a.y] > h[b.y];
    return a.z < b.z;
}

int find(int x) {
    if (parent[x] != x) parent[x] = find(parent[x]);
    return parent[x];
}

// Kruskal算法求最小生成树的边权和
LL kruskal() {
    for (int i = 1; i <= n; i++) parent[i] = i;
    sort(e + 1, e + 1 + pos, cmp);
    LL res = 0;
    for (int i = 1; i <= pos; i++) {
        int x = e[i].x, y = e[i].y, z = e[i].z;
        // 只考虑可达的景点
        if (!st[x] || !st[y]) continue;
        int fx = find(x), fy = find(y);
        if (fx != fy) {
            parent[fx] = fy;
            res += z;
        }
    }
    return res;
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> h[i];
    for (int i = 1; i <= m; i++) {
        int x, y, z;
        cin >> x >> y >> z;
        // 双向存储边（因为可能从y滑到x，只要h[y]>=h[x]）
        if (h[x] >= h[y]) edges[x].push_back({y, z});
        if (h[y] >= h[x]) edges[y].push_back({x, z});
    }

    // 从景点1出发DFS
    dfs(1);
    // Kruskal求最短滑行距离
    LL dist_sum = kruskal();

    cout << cnt << " " << dist_sum << endl;

    return 0;
}

---

总结

最小生成树是图论中的基础算法，也是面试和算法竞赛中的高频考点。希望本文能帮助你彻底掌握这一知识点，在后续的学习和实践中灵活运用。如果有任何疑问或建议，欢迎在评论区留言讨论！