每日激励:"不设限和自我肯定的心态:I can do all things。 --- Stephen Curry"
**绪论:
本章将先通过链表常用方法+操作总结帮助你快速了解我们后面会用到的方法以及操作,然后会通过5道由简单到复杂的综合题帮你巩固,本章主要为了让你能快速认识并能解决大部分链表相关的题。早关注不迷路,话不多说安全带系好,发车啦(建议电脑观看)。**
链表
总结链表常用技巧:
-
画图!!!(不仅仅是链表而是大多数数据结构),画图就会变得更加直观形象和便于理解。
-
引入虚拟 "头" 结点,在算法中链表一般都是不带头(哨兵/头结点)节点的单链表为什么说要利用哨兵呢
- 当我们引入头结点后我们就能非常方便的处理链表
- 便于处理边界情况:当不提前引入虚拟节点就需要判断头结点的情况,而引入后即使头结点为空我们也能通过虚拟节点的特判快速处理
- 方便对链表操作:因为常常我们需要返回新链而引入哨兵这个新链就在newhead->next里面,所以在对新链的操作中,不用考虑头位置在哪了,只需要考虑新链的操作
- 代替空指针作为当做空来指向,方便头插完成逆序(这个主要体现与逆序prev指针的初始值)

- 当我们引入头结点后我们就能非常方便的处理链表
-
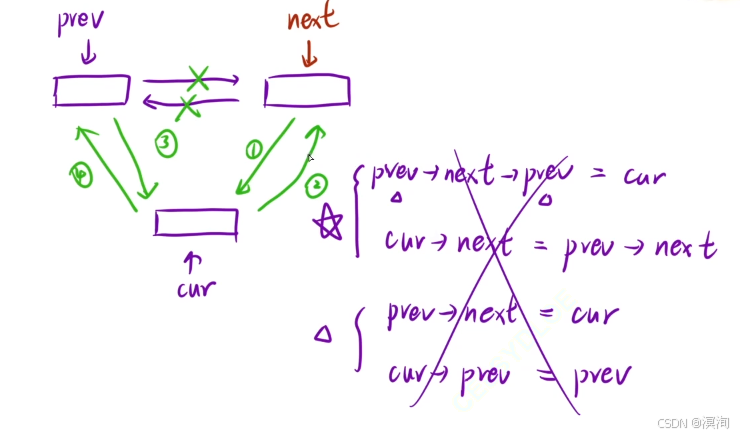
不要吝啬空间,大胆去定义指针变量来辅助在链表中的操作(如下图若不使用next变量,你就需要执行右边一大堆步骤,还要考虑内部的顺序,而若先记录了下一个位置,那么这些问题都将迎刃而解,所以不要吝啬那4byte的空间)所以大胆的定义通俗易懂方便操作的变量
-
快慢双指针
cpp/** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode(int x) : val(x), next(NULL) {} * }; */ class Solution { public: ListNode *detectCycle(ListNode *head) { if(head == nullptr) return nullptr; //使用快慢指针 ListNode* guard = head; ListNode* fast = head,*last = head; while(fast) { if(fast->next != nullptr){ fast = fast->next->next; } else{ return nullptr; } last = last->next; if(fast == last) { //设 a = 从开头到入口(不包括入口),k代表走的步数 //当fast和last相遇后,此时last = k,fast = 2k //设last在圈中走m步数与fast相遇,即:k = a + m //而fast = 2k(last + k),就代表从相遇点再到相遇带是k步 //而 k = a + m,而 m = 从入口到相遇点 //所以最后就代表,从相遇点再走a步就能到达入口 //所以现在一个指针从开始走,一个指针从相遇点走,当相遇的时候就代表说入口 fast = guard; while(fast != last) { fast = fast->next; last = last->next; } return fast; } } return nullptr; } };
总结:
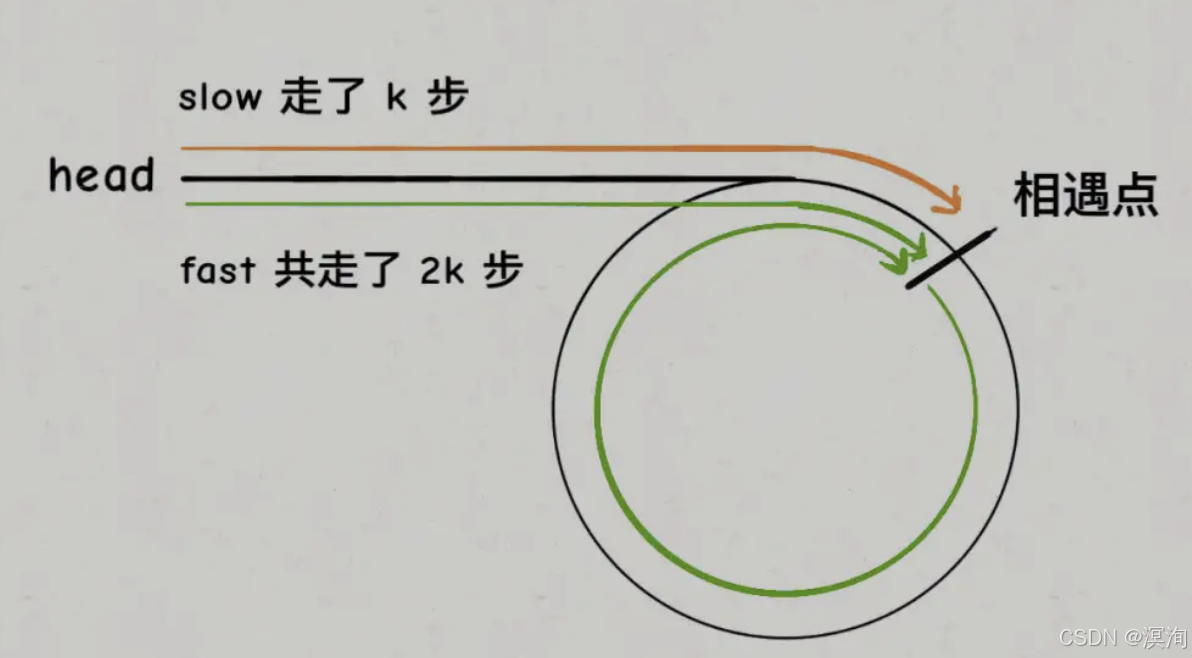
- 设 a = 从开头到入口(不包括入口),k代表走的步数
- 当fast和last相遇时,
last = k,fast = 2k(因为快慢指针)- 这就代表着fast在圈内从相遇点到相遇点的距离为k,因为从开始到相遇点的距离就是last走的步数k,相加就是2k(如下第一张图)
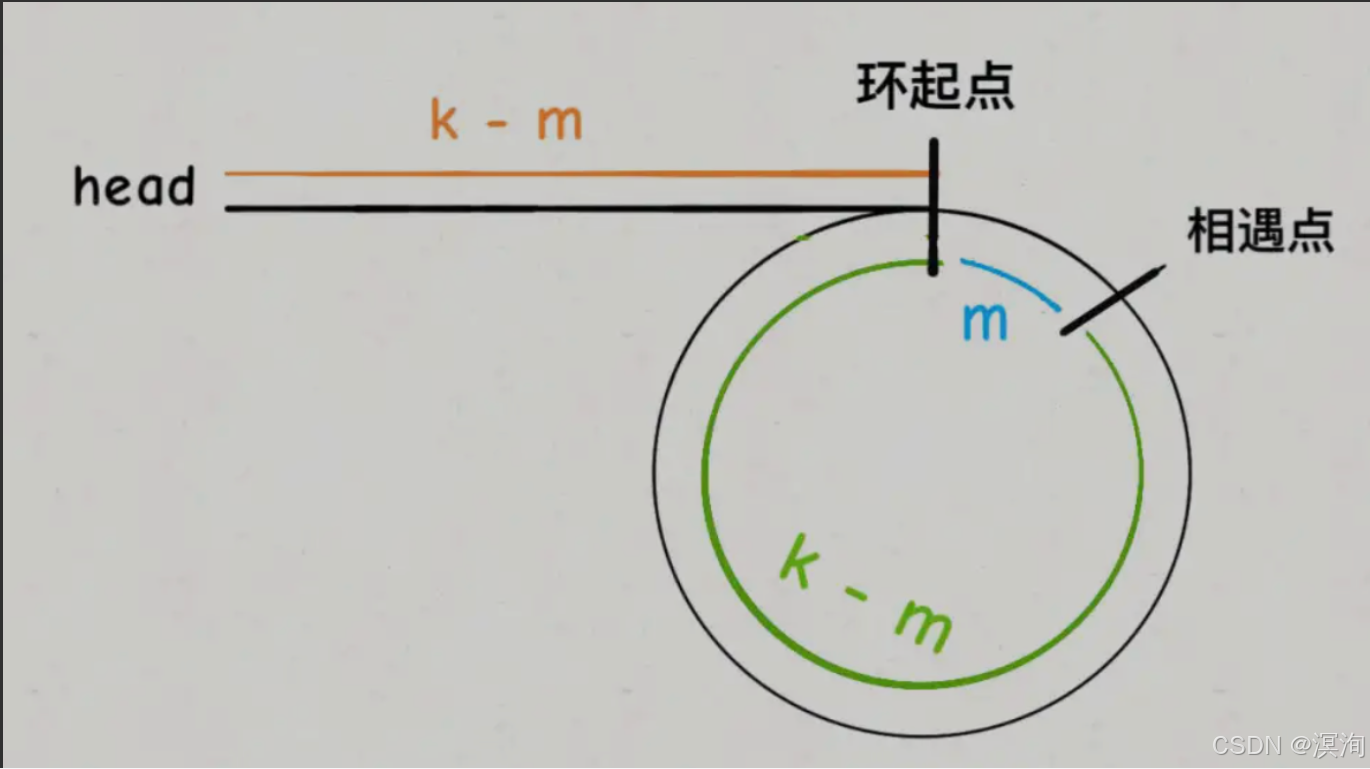
- 现在设从入口到相遇点的距离是m,则从起始到入口的距离就是 k - m(如下第二张图)
- 结合前面fast在圈内从相遇点到相遇点的距离为k,所以若不到相遇点就是 k - m 了
- 也就是说:从相遇点到入口 = 从起点到入口,这样将一个指针回到起点然后两个指针同时走最终就一定会到入口相遇走 k - m 步
当相遇后都各自在一步步走就将在环起点相遇
附:作者LeetCode静静再次精简理解:直接想当fast和slow相遇的点,slow走了k步(a从开始到入环 + b环内走的路程),不管fast走了多少,因为都是在圈中,而他们相遇点是 b,所以在走a步也就是将slow放回起点,fast不变,两个同时走最终将在入环点相遇(因为减掉了b也就是减掉了slow在环中走的路程)
-
cpp
/** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode() : val(0), next(nullptr) {} * ListNode(int x) : val(x), next(nullptr) {} * ListNode(int x, ListNode *next) : val(x), next(next) {} * }; */ class Solution { public: ListNode* removeNthFromEnd(ListNode* head, int n) { //删除倒数第n个,且遍历一遍 //当我们画出图,看删除节点,让快指针先走n步,然后慢指针在和快指针同步走,当快指针走到结束时,慢指针的下一个位置就是删除的节点 //原因,快指针始终只是比慢指针快n步,所以当快指针结束慢指针所在的位置也就是倒数n位置 //所以我们可以定义三个指针:prev slow fast if(head == nullptr) return nullptr; ListNode* prev= nullptr; ListNode* slow = head,*fast = head; while(n--) // fast先走n步 if(fast) fast = fast->next; while(fast) { fast = fast->next; if(slow) { prev = slow; slow = slow->next; } } ListNode* next = slow->next; if(prev == nullptr){//代表进行头删即可 head = next; } else{//当结束后slow位置就是要删除的值的位置 prev->next = next; } delete slow; return head; } };
这题就在于技巧分析得出:让fast指针先走n步,然后slow在开始走,当fast结束后,slow的下一个位置就是要删除的节点
链表中的常用操作:
- 创建新节点(new)
- 尾插(这里通常需要创建一个prev(tail)尾指针记录链表尾部的地址,这样当我们需要插入的时候就能够直接通过这个指针进行尾插)

- 头插(如下图,当我们引入虚拟节点后,对链表进行头插就会非常方便)
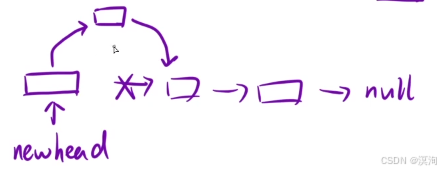
- 同上当你会头插你就能快速的做出来逆序链表:
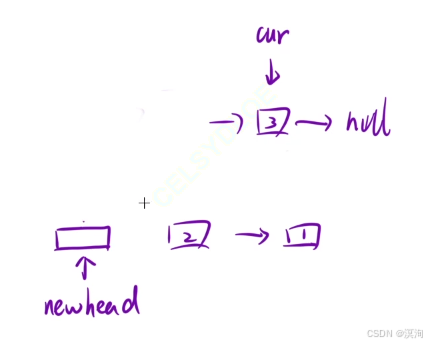
- 同上当你会头插你就能快速的做出来逆序链表:
请一定要将上面总结的观看完,上述都是下述的基础或者说总结而来,当你把上述内容看完,再来做就能达到事半功倍的效果!
具体训练:
两数相加
题目:
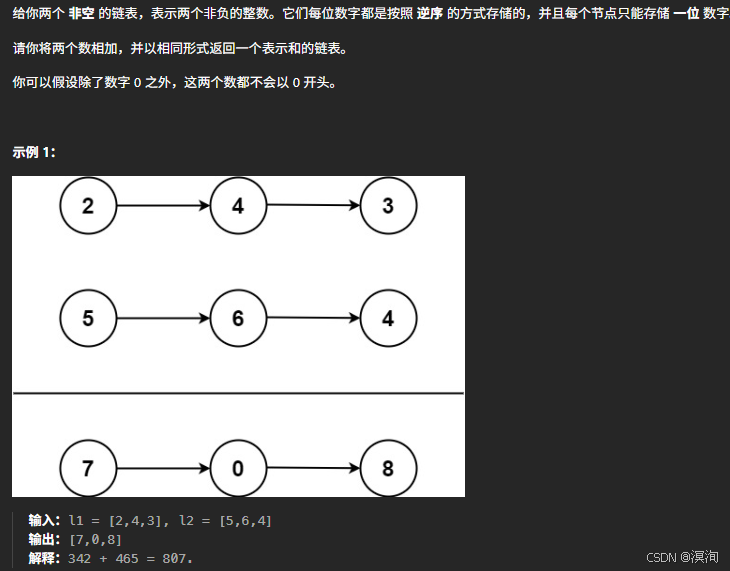
分析题目并提出,解决方法:
- 其中链表内存储的数据都是逆序的数值,所以需要先逆序的取出来
- 最后在把算出来的值,逆序创建一个链表
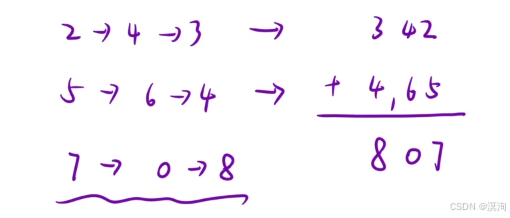
题解核心逻辑:
- 解法:模拟两数相加的过程即可(如下图)
- 其中技巧中的巧用虚拟头结点这里也就可以用上了
- 若不使用虚拟头结点,还需要记录head节点
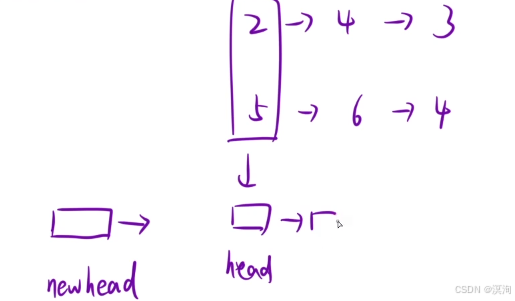
- 当使用了虚拟头结点就很顺畅了直接连接在虚拟节点后面即可(操作:头插)
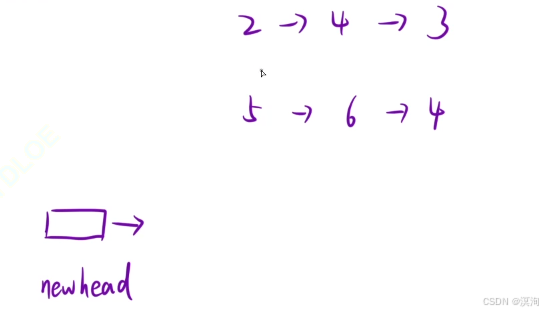
- 若不使用虚拟头结点,还需要记录head节点
- 后面就是使用双指针遍历两个链表,同时移动并相加,得到值t,将t的个位取出来,后面的t就是进位,所以后面需要加上
- 其中取出来的个位就创建为节点连到链表中即可
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
//虚拟头结点
ListNode* newhead = new ListNode();
ListNode* cur = newhead;
//创建变量记录计算结果和进位
int t = 0;
// //2. 遍历两个链表并相加
// while(l1 && l2)
// {
// t = l1->val + l2->val + t;//加上t是因为可能会有进位
// l1 = l1->next;
// l2 = l2->next;
// //取出个位创建节点
// ListNode* newnode = new ListNode(t % 10);
// t /= 10;
// cur->next = newnode;
// cur = cur->next;
// }
// //3. 处理长度不一致
// while(l1)
// {
// t = l1->val + t;//这里就只用处理l1了
// l1 = l1->next;
// ListNode* newnode = new ListNode(t % 10);
// t /= 10;
// cur->next = newnode;
// cur = cur->next;
// }
// while(l2)
// {
// t = l2->val + t;//这里就只用处理l1了
// l2 = l2->next;
// ListNode* newnode = new ListNode(t % 10);
// t /= 10;
// cur->next = newnode;
// cur = cur->next;
// }
// if(t != 0) {
// ListNode* newnode = new ListNode(t);
// cur->next = newnode;
// cur = cur->next;
// }
// 优化在一起:从上面的分开来的进行总结得出:
while(l1 || l2 || t) //当l1/l2走完后仍然要继续执行,并且t可能也会到最后剩1所以也要处理
{
if(l1)
{
t += l1->val;
l1 = l1->next;
}
if(l2)
{
t += l2->val;
l2 = l2->next;
}
ListNode* node = new ListNode(t%10);
t /=10;
cur->next = node;
cur = cur->next;
}
cur = newhead->next;
delete newhead;
return cur;
}
};两两交换链表中的节点
题目:
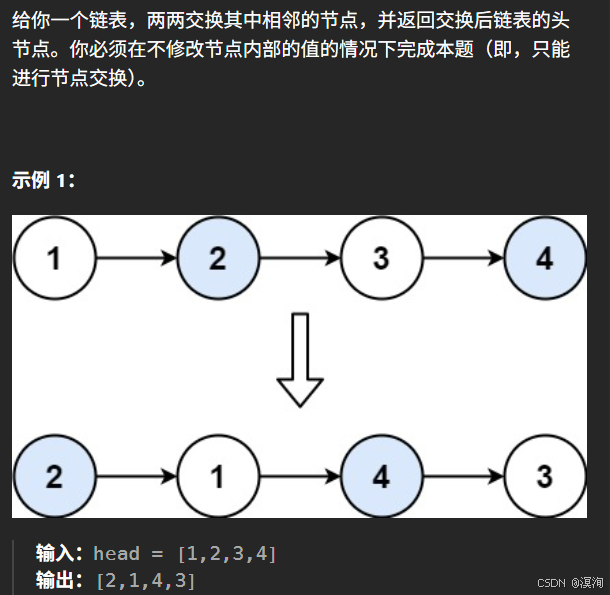
分析题目并提出,解决方法:
分析题目不难得出就是将两两相邻节点的交换,具体如下图
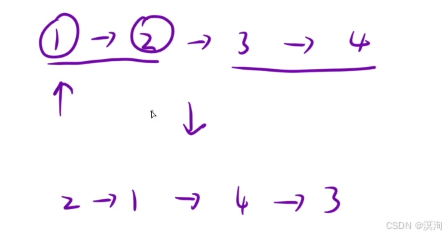
解法1:递归
解法2:循环,迭代(模拟)
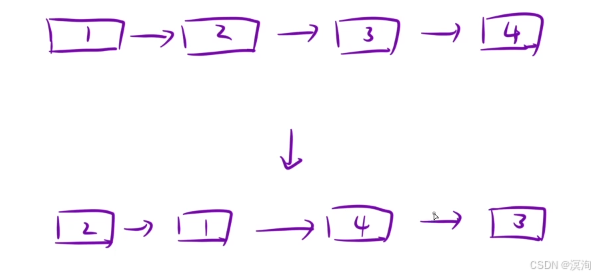
- 引入虚拟头结点节点(下图为不引入此时需要对12节点单独处理,而若引入虚拟节点12和后面的操作就是保持一致的了)
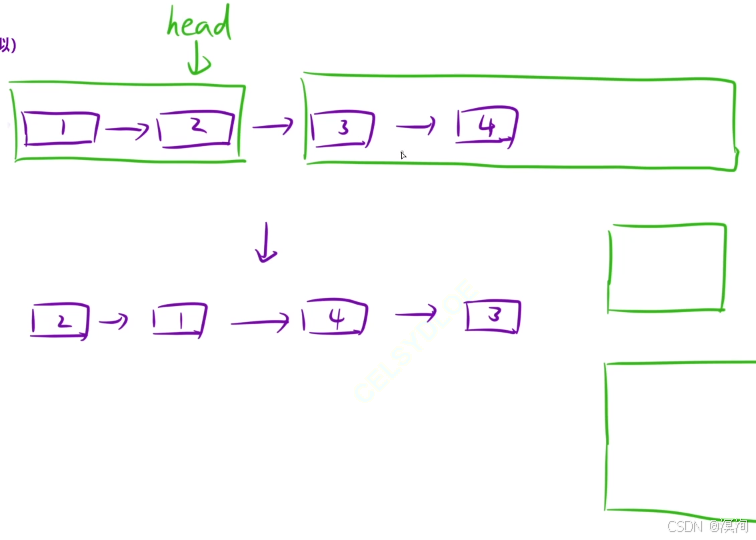
- 并且不要吝啬变量方便操作(如下图,当设置变量后就能非常轻便的进行链的操作)
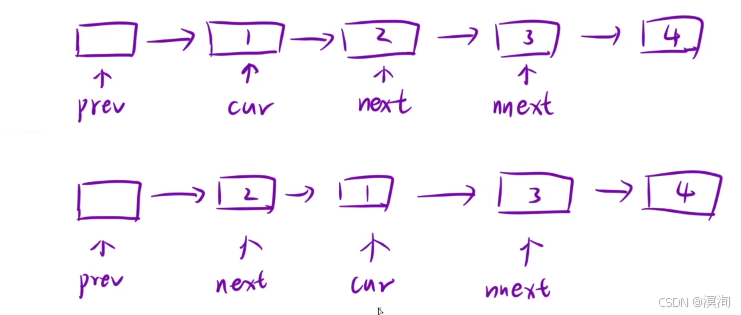
- 当从上的链表修改为下面的链表后,就可以将整体向后移动
-
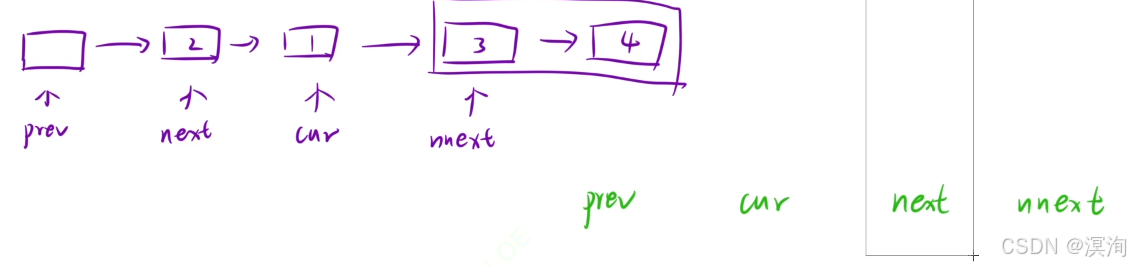
prev、cur、next、nnext的移动如下图:
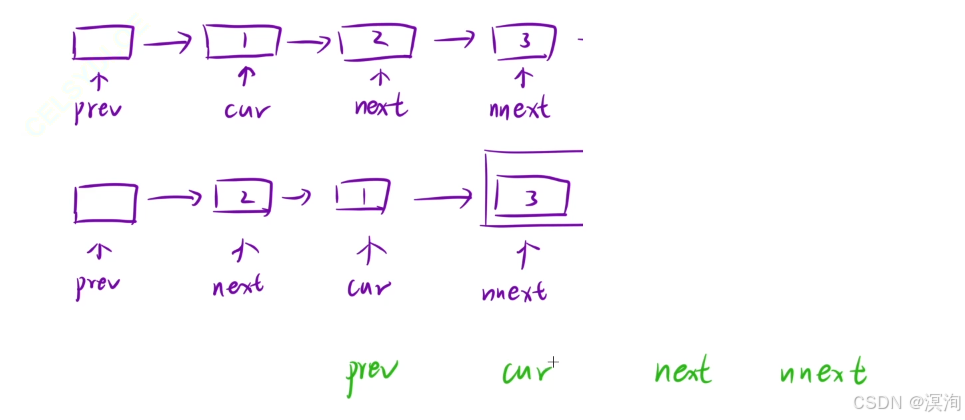
-
其中注意的是当 cur 或者 next为空时则代表结束(具体如下图情况,分别是奇数个元素和最终结束结果的情况)
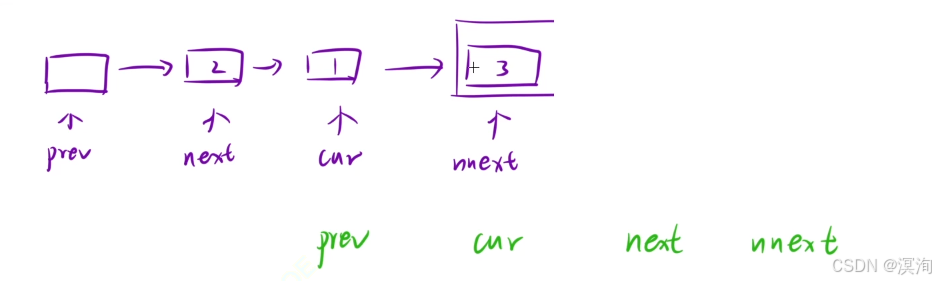
-
题解核心逻辑:
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
//递归实现版本:
// if(head == nullptr || head->next == nullptr){
// return head;//返回当前结点
// }
// //子问题:
// //1. 获取dfs后面的头结点
// ListNode* tmp = swapPairs(head->next->next);
// head->next->next = head;
// ListNode* ret = head->next;
// head->next = tmp;
// return ret;
//迭代:
ListNode* newhead = new ListNode(0,head);
if(head == nullptr || head->next == nullptr) return head;
ListNode* prev = newhead,*cur = head,*next = head->next,*nnext = next->next;
// if(cur == nullptr) next = nullptr;
// else next = cur->next;
// if(next == nullptr) nnext = nullptr;
// else nnext = next->next;
while(next && cur)
{
prev->next = next;
cur->next = nnext;
next->next = cur;
prev = cur;// 这里是cur,和先修改prev在修改cur
cur = nnext;
if(cur) next = cur->next;
if(next) nnext = next->next;
}
prev = newhead->next;
delete newhead;
return prev;
}
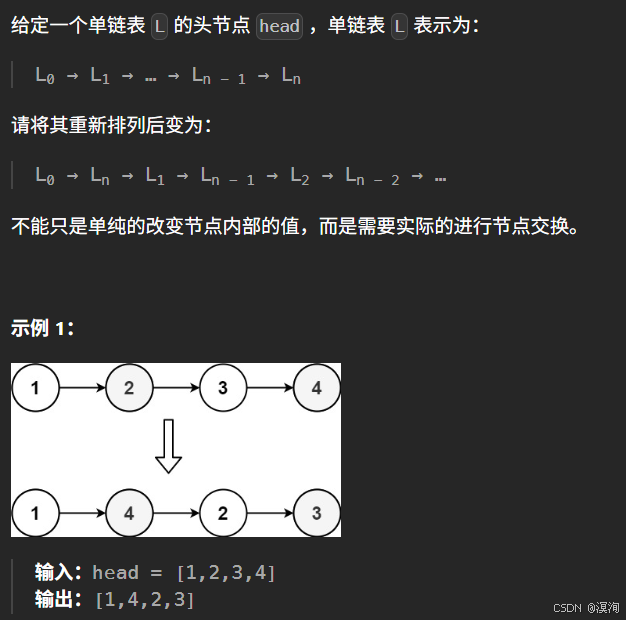
};重排链表⭐⭐⭐
题目:
分析题目并提出,解决方法:

不难理解就是按给的排列形式将原本的链表修改为给定的排序方法
解法:模拟
通过对题目的分析,可以把他看成两个链表的合并,这两个链表分别是数组的前半段和后半段的逆序(具体如下图)
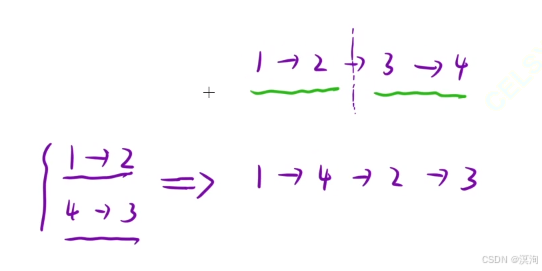
题解核心逻辑:
那么这题的解法就是:
- 先将链表分成两部分,找中间节点(快慢双指针)
- 将第二部分逆序(双指针/头插法)
- 合并两个链表:先使用前半段链表的节点(双指针)
不难发现这题综合性还是比较高的,所以面试也会常考。
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
void reorderList(ListNode* head) {
//1. 找到链表的中间元素(快慢指针)
ListNode* fast = head,*slow = head;
ListNode* l1last = nullptr;
while(fast)
{
l1last = slow;
slow = slow->next;
if(fast->next == nullptr) break;
fast = fast->next->next;
}
l1last->next = nullptr;//把两个链表断开
//此时slow就是后半段的开始
ListNode* l2head = new ListNode(0);//给 l2 一个虚拟头结点
ListNode* l2 = slow;//此时的slow是第二个链表的开始,若为奇数不要中间节点
//通过l2和l2的虚拟头结点遍历自身完成头插逆序
while(l2)
{
ListNode* next = l2->next;
l2->next = l2head->next;
l2head->next = l2;
l2 = next;
}
l2 = l2head->next;//l2head->next就是逆序后的新l2
delete l2head;//l2没用了就释放了吧
//3. 合并两个链表
ListNode* l1 = head;
ListNode* newhead = new ListNode(0,l1);//重新定义整个链表的虚拟节点,并将所有节点都放到newhead后面
while(l1 && l2)
{
ListNode* next1 = l1->next,*next2 = l2->next;//记录下一个位置,因为下面要断开了
l1->next = l2;
l2->next = next1;
l1 = next1;
l2 = next2;
}
head = newhead->next;
delete newhead;
}
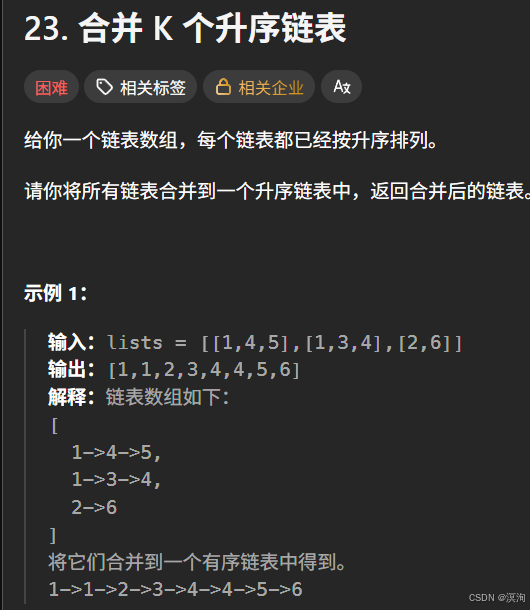
};合并 K 个升序链表
题目:
分析题目并提出,解决方法:
分析示例一不难知道如下图:就是将给的多个升序链表合并为一条链表
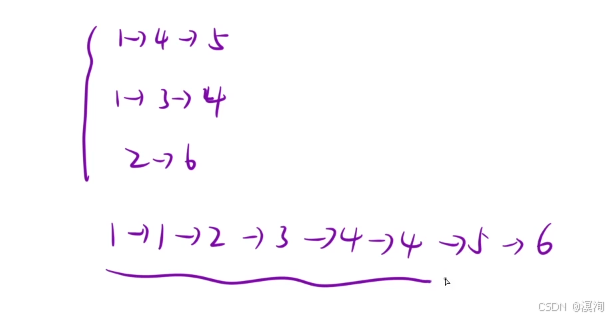
解法一:暴力解法
本质就和合并两个有序链表的延展,将多个链表先合并两个链表为一个链表,然后将这个新的链表再继续和其他链表进行合并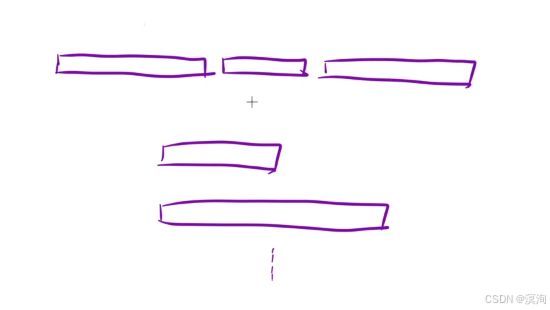
解法二:利用优先级队列
- 在利用类似之前合并两个链表的思想:同时比较多个链表(比较两个链表)找出较小的值然后添加到newhaed链表后
- 其中因为比较比较麻烦所以映入一个优先级队列(小根堆:最小的元素一致在堆顶),来快速的对多个数据的比较进行优化,具体比较方法:如下图首先将链表最开始的三个元素放进去,此时第一个链表的元素最小就从小根堆中取出来,然后再把第一个链表的第二个元素放进小根堆
- 这样就能不断的比较然后快速的取出较小的元素放到newhead后面,最终完成合并
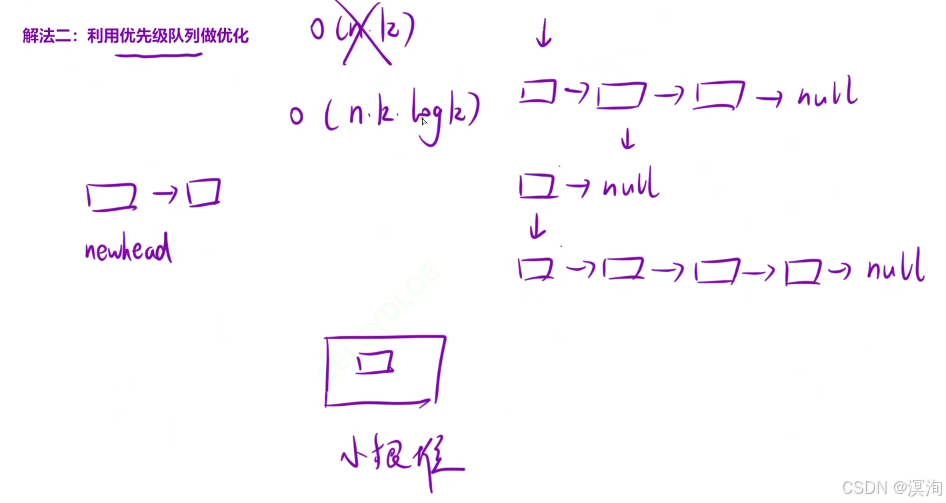
时间复杂度:O(nKlogk):因为n个元素K个链表也就是总个数、logk小根堆一次的比较时间复杂度
使用优先级队列(priority_queue<int,vector<int>,less<int>其中默认是大根堆)能够同时比较数量是未知的情况时的值,也就是说当一个数组中数量是未知的而此时有需要进行比较不妨可以使用一下优先级队列
解法三:分治 - 递归
递归思想:
- 将多个链表(注其中下图的一个节点是一个链表而不是一个节点)分成两份,前半段合并为一个,后半段合并一个
- 最后将这形成的新的两个链表合并为一个
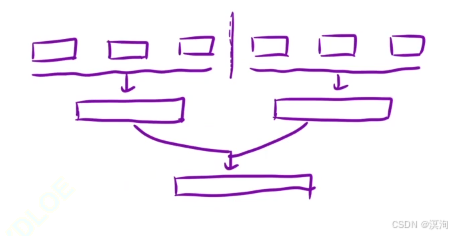
对于左右两边的多个如何进行操作呢,其实本质同上,从中间劈开两部分,然后再各自处理,直到值最小情况(只有一个链表),这样来看就非常想归并了(这里不太熟悉的话建议看blog)。
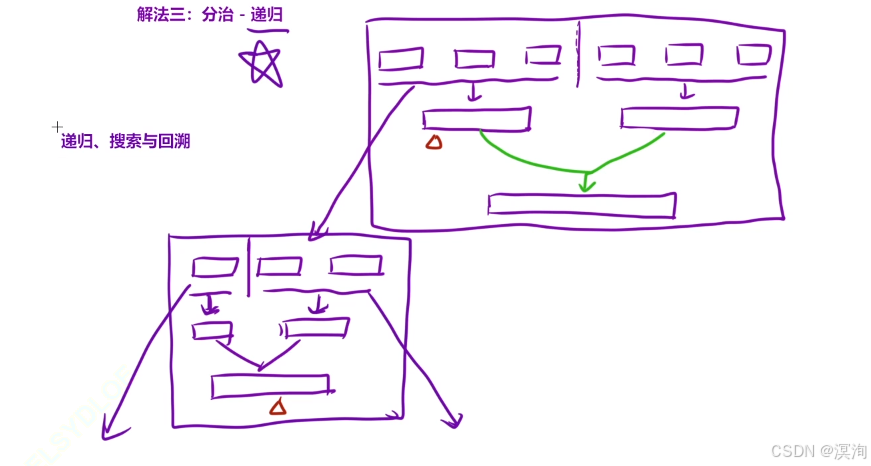
时间复杂度:同样是O(n * k * logk):n个节点k个链表执行logk次合并
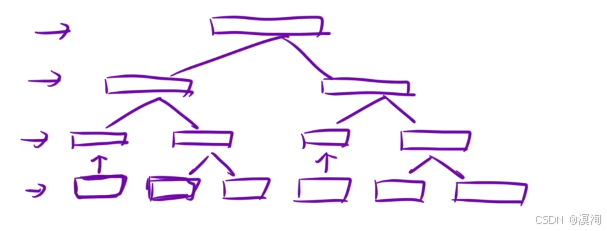
题解核心逻辑:
解法二:
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
struct cmp{
bool operator()(const ListNode* node1,const ListNode* node2)
{
return node1->val > node2->val;
}
};
ListNode* mergeKLists(vector<ListNode*>& lists) {
//从合并两个有序链表变成合并K个有序链表
//核心思想保持不变,通过遍历K个链表,将较小的值添加到新链表后面
//其中比较过程通过一个优先级队列进行优化:将比较的K个元素丢进小根堆,取出堆顶元素,再将取出的堆顶元素的下一个节点丢进来完成比较
//所以这里总结下:当需要同时比较多个值或者未知个个数的值时,就能给他丢进优先级队列中来进行比较
priority_queue<ListNode*,vector<ListNode*>,cmp> pq;//注意默认是大根堆
for(auto node : lists)//首先将K个节点插入
if(node) pq.push(node); // 其中一定要注意着里要判断一下防止传递空进去
ListNode* newhead = new ListNode(0);
ListNode* prev = newhead;
while(!pq.empty())
{
ListNode* node = pq.top();
pq.pop();
prev->next = node;
prev = prev->next;
if(node->next) // 其中一定要注意着里要判断一下防止传递空进去
pq.push(node->next);
}
prev = newhead->next;
delete newhead;
return prev;
}
};解法三:
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
return merge(lists, 0, lists.size() - 1);
}
ListNode* merge(vector<ListNode*>& lists, int left, int right) {
if (left > right)
return nullptr;
if (left == right)
return lists[left];
// 1. 平分数组
int mid = left + right >> 1;
// [left, mid] [mid + 1, right]
// 2. 递归处理左右区间
ListNode* l1 = merge(lists, left, mid);
ListNode* l2 = merge(lists, mid + 1, right);
// 3. 合并两个有序链表
return mergeTowList(l1, l2);
}
ListNode* mergeTowList(ListNode* l1, ListNode* l2) {
if (l1 == nullptr)
return l2;
if (l2 == nullptr)
return l1;
// 合并两个有序链表
ListNode head;
ListNode *cur1 = l1, *cur2 = l2, *prev = &head;
head.next = nullptr;
while (cur1 && cur2) {
if (cur1->val <= cur2->val) {
prev = prev->next = cur1;
cur1 = cur1->next;
} else {
prev = prev->next = cur2;
cur2 = cur2->next;
}
}
if (cur1)
prev->next = cur1;
if (cur2)
prev->next = cur2;
return head.next;
}
};K 个一组翻转链表
题目:
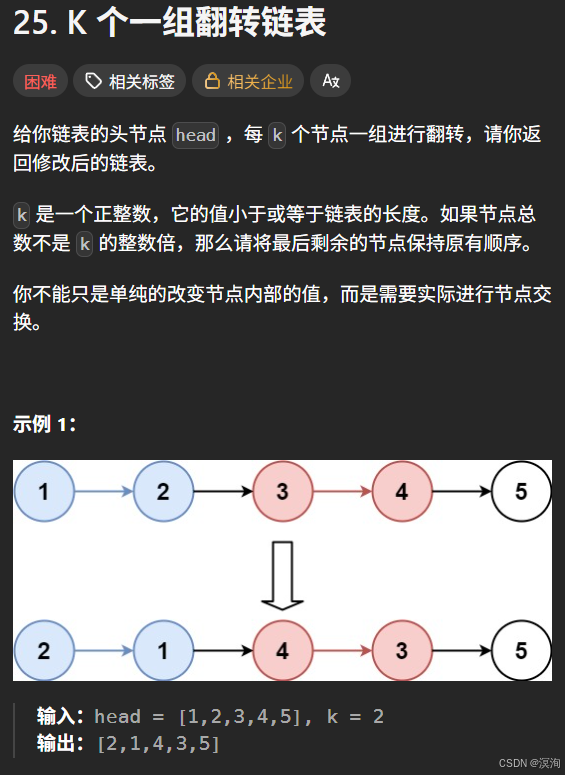
分析题目并提出,解决方法:
根据示例一:不难分析出如下图,题目给定一个k值只需要翻转k值以内的链表,不够k值的则不用翻转(如下5节点)
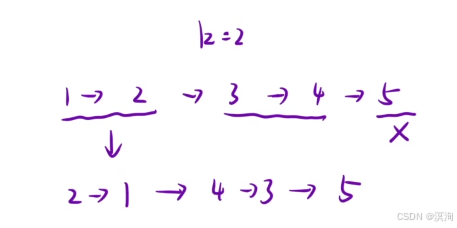
解法:模拟
- 先求出需要逆序多少组:n(遍历链表一次即可知道)
- 重复n次,长度为 k 的链表的逆序即可
- 逆序:头插法
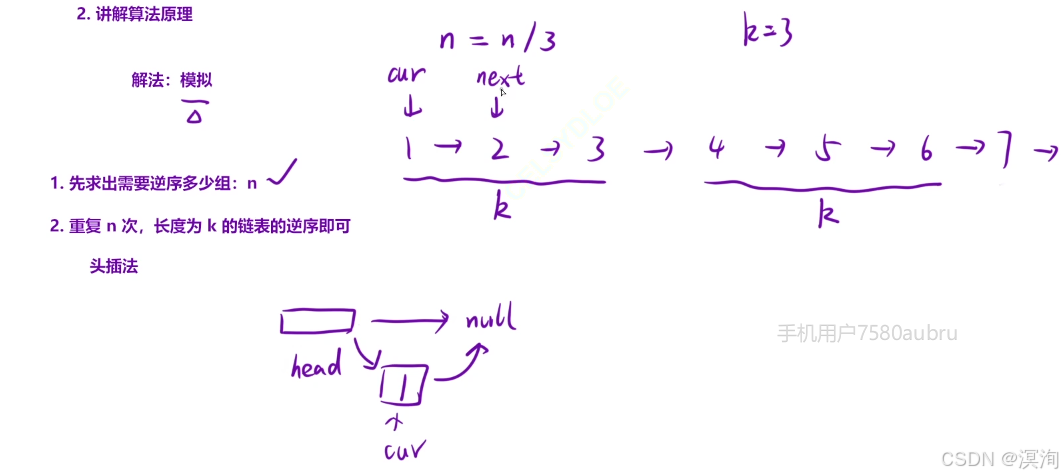
其中注意:
因为这里是一次性头插 k 个然后又重新头插 k 个所以连接的位置就需要记录下,使用一个tmp指针记录最开始节点的位置,当翻转过后他就能到链表的最后,也就是下一个要翻转链表的连接点,同时把prev指向这里代表新链表的尾(方便后续连接)
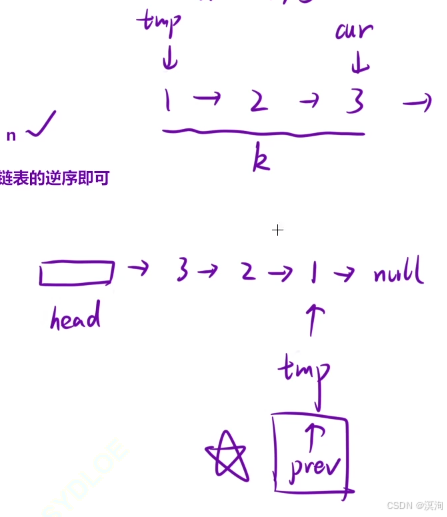
题解核心逻辑:
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
//模拟
//1. 遍历数组找到需要翻转的次数
ListNode* cur = head;
int n = 0;
while(cur)
{
n++;
cur = cur->next;
}
n = n / k;//翻转次数就为 n / k
//2. 模拟翻转过程
ListNode* newhead = new ListNode(0);//虚拟头结点
ListNode* prev = newhead,* tmp = head;
cur = head;
while(n--)//翻转n次
{
int kt = k;
while(kt--)
{
ListNode* next = cur->next;//记录防止丢失
//头插
cur->next = prev->next;
prev->next = cur;
cur = next;
}
prev = tmp;
tmp = cur;
}
if(cur) prev->next = cur;
prev = newhead->next;
delete newhead;
return prev;
}
};