文章目录
-
- [what 's piovt?](#what 's piovt?)
-
- [How? how to find the pivots?](#How? how to find the pivots?)
- 为什么要找主元所在的列?
"找主元"是矩阵运算中最基础也最核心的技能。
总结一句话:
在 RREF 中,每一行最左边的那个"1"就是主元;这些"1"在哪一列,哪一列就是主元列。
what 's piovt?
piovt: 在RREF(行最简行矩阵)中,每一行第一个非零的"1",成为主元。
简单来说,**主元(Pivot)**就是 RREF(行最简形矩阵)中,每一行第一个非零的"1"。
How? how to find the pivots?
我们可以把找主元的过程想象成 "下台阶"。
- 看着刚才算出来的 RREF 矩阵
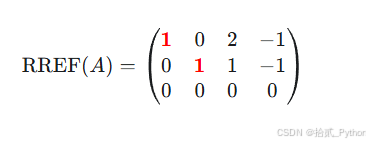
怎么找主元?(三步走)
- 看第一行: 从左向右,第一个不为零的数字
- 第一个主元在第一列 1
- 看第二行: 同理
- 第二个主元在第二列、
- 同理, 全为0.没有主元、
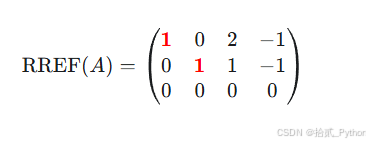
matlab
\text{RREF}(A) =
\begin{pmatrix}
\color{red}{\mathbf{1}} & 0 & 2 & -1 \\
0 & \color{red}{\mathbf{1}} & 1 & -1 \\
0 & 0 & 0 & 0
\end{pmatrix}
为什么要找主元所在的列?
在**"满秩分解"中非常关键。**
主元所在的列,代表了原矩阵 A 的"骨架"。
