计算机图形学 模型矩阵的逆矩阵：如何从“世界”回归“局部”？

目录

[一、 引言：为什么我们需要"回去"？](#一、 引言：为什么我们需要“回去”？)

[二、 核心理论：逆矩阵的几何意义](#二、 核心理论：逆矩阵的几何意义)

[1. 数学推导](#1. 数学推导)

[2. 几何解释](#2. 几何解释)

[三、 实战应用：为什么这很重要？](#三、 实战应用：为什么这很重要？)

场景：点击一个歪歪扭扭的盒子

[四、 代码实现（基于 Three.js）](#四、 代码实现（基于 Three.js）)

[1. 使用封装好的 API](#1. 使用封装好的 API)

[2. 手动实现（还原数学原理）](#2. 手动实现（还原数学原理）)

五、更通俗易懂的例子

核心逻辑

代码实现

---

在 3D 开发（如 Three.js、WebGL）中，我们经常使用模型矩阵 将物体从局部坐标系转换到世界坐标系。但你是否思考过，如何反向操作？现在从数学原理与几何意义出发，探讨"模型矩阵的逆矩阵"在坐标转换中的核心作用，并结合射线拾取（Raycasting）等实际场景，

一、 引言：为什么我们需要"回去"？

我们最熟悉的流程通常是这样的：

1. 在建模软件里建好一个模型（局部坐标，Local Space）。

2. 把它加载到场景中，设置 position、rotation、scale。

3. 渲染引擎通过 模型矩阵 自动帮我们把顶点的局部坐标转换成了世界坐标，最终显示在屏幕上。

公式很简单：

但是，在很多高阶交互场景下（比如鼠标点击检测、父子层级变换），我们需要反着来------已知一个世界坐标中的点，想知道它相对于某个物体中心的坐标是多少。

这就涉及到了线性代数中一个极其优美的概念：逆矩阵（Inverse Matrix）。

二、 核心理论：逆矩阵的几何意义

如果说模型矩阵M 是一张"单程票"，把点从家（局部）带到了世界广场；那么M的逆矩阵就是一张"返程票"，把点从世界广场送回家。

1. 数学推导

根据线性代数的基本性质：

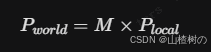
2. 几何解释

• 模型矩阵 (M)：记录了物体是如何平移、旋转、缩放的。

• 逆矩阵 (M的逆) ：记录了如何撤销这些平移、旋转、缩放。

一句话总结 ：模型矩阵是将局部坐标系转换到世界坐标系；模型矩阵的逆，就是将世界坐标系转换回局部坐标系。

三、 实战应用：为什么这很重要？

在实际工程中，它解决了一个巨大的痛点：碰撞检测与交互（Raycasting）。

场景：点击一个歪歪扭扭的盒子

假设场景里有一个被旋转了 45 度、又被缩放过的盒子（Box）。你需要判断鼠标点击出的射线（Ray）是否击中了这个盒子。

• 困难的做法（在世界坐标系算）：

  你需要计算射线与一个"倾斜的立方体"的交点。这涉及复杂的立体几何运算，计算量大且容易出错。

• 聪明的做法（在局部坐标系算）：

  利用逆矩阵！

  1. 获取盒子的模型矩阵，求逆，得到 M的逆

  2. 用 M的逆 把鼠标发出的射线（World Ray）变换一下，变回盒子的局部空间。

  3. 奇迹发生了：在局部空间里，盒子永远是正正方方的（Axis-aligned），中心通常在原点。

  4. 我们只需要判断"一条歪射线"和"一个正盒子"是否相交。这仅仅是简单的 if (x > minX && x < maxX) 的运算，速度快了几个数量级！

Three.js 的 Raycaster 底层正是利用了这个逻辑，才实现了高效的拾取。

四、 代码实现（基于 Three.js）

在 Three.js 中，虽然封装好的 worldToLocal 方法屏蔽了细节，但理解底层原理不是更香吗？

1. 使用封装好的 API

const mesh = new THREE.Mesh(geometry, material);
scene.add(mesh);

// 假设有一个世界坐标点
const worldPoint = new THREE.Vector3(10, 5, 0);

// 直接转换回 mesh 的局部坐标
mesh.worldToLocal(worldPoint);

console.log(worldPoint); // 输出该点相对于 mesh 中心的位置

2. 手动实现（还原数学原理）

const worldPoint = new THREE.Vector3(10, 5, 0);

// 1. 获取物体的世界变换矩阵
const matrixWorld = mesh.matrixWorld;

// 2. 计算逆矩阵
const inverseMatrix = new THREE.Matrix4();
inverseMatrix.copy(matrixWorld).invert(); // 求逆

// 3. 应用逆矩阵： P_local = M_inv * P_world
const localPoint = worldPoint.clone().applyMatrix4(inverseMatrix);

console.log(localPoint);

五、更通俗易懂的例子

判定一个点是否在一个box内呢，知道box的模型矩阵及点的世界坐标，

核心逻辑

• 困难模式（世界坐标系）： 你的 Box 是歪的（被旋转过），点也是任意的。你需要判断点是否在六个倾斜面的"中间"，这需要算点到平面的距离，非常麻烦。

• 简单模式（局部坐标系）：

  1. 利用 模型矩阵的逆 把世界坐标的点变换回 Box 的局部坐标

  2. 在局部坐标系里，Box 永远是正正方方的（通常中心在原点，或者是已知的 min/max 范围）。

  3. 你只需要做最简单的大小比较（AABB 检测）。

代码实现

// 假设 boxMesh 是你的物体，pointWorld 是世界坐标中的点(Vector3)

function isPointInBox(pointWorld, boxMesh) {
    // 1. 获取逆矩阵 (World -> Local)
    // 注意：在 Three.js 中，为了性能，最好把 inverseMatrix 缓存起来，不要每帧 new
    const inverseMatrix = boxMesh.matrixWorld.clone().invert();

    // 2. 将世界坐标点转换到局部坐标系
    const pointLocal = pointWorld.clone().applyMatrix4(inverseMatrix);

    // 3. 获取 Box 的局部几何边界 (AABB)
    // 如果是标准几何体，通常 geometry.boundingBox 就可以拿到 min 和 max
    // 如果没有计算过，需要先 boxMesh.geometry.computeBoundingBox();
    const min = boxMesh.geometry.boundingBox.min;
    const max = boxMesh.geometry.boundingBox.max;

    // 4. 简单的 AABB 判定
    if (pointLocal.x >= min.x && pointLocal.x <= max.x &&
        pointLocal.y >= min.y && pointLocal.y <= max.y &&
        pointLocal.z >= min.z && pointLocal.z <= max.z) {
        
        return true; // 在里面！
    }

    return false; // 在外面
}