机器学习算法三：决策树

前一篇博客我们学习了逻辑回归的三种优化方法，但是逻辑回归主要解决的是二分类的问题，如果是更多的分类我们怎么办呢？这就引出我们今天的算法：决策树。

一、决策树核心原理

决策树的核心是通过"树状结构"实现决策：以数据的特征作为树的"内部节点"（包括根节点），以数据的标签（决策结果）作为树的"叶节点"；主流构建方式为二叉树（也支持多叉树，如ID3算法），通过逐层分裂特征，最终让每个叶节点对应明确的标签类别。

二、决策树构建流程

核心流程是"递归分裂"：

从所有特征中选择一个作为"根节点"，根据该特征的划分规则（如二分类特征的"是/否"、连续特征的"大于/小于阈值"），将原始数据集拆分为2个（二叉树）或多个（多叉树）子集；
把每个子集看作新的"待分裂数据集"，对每个子集重复步骤1（选择该子集对应的最优特征作为内部节点）；
当满足停止条件（如子集所有样本标签一致、样本数量过少、特征已分裂完毕）时，停止分裂，将该子集对应的标签作为"叶节点"；
重复上述过程，直至所有子集都成为叶节点，决策树构建完成。

三、核心问题：如何选择最优分裂节点（三种核心算法）

决策树构建的关键是"每次都选对分裂特征"，否则会导致树结构冗余、预测不准。行业内有三种经典选择标准，对应三种算法：ID3算法（信息增益）、C4.5算法（信息增益比）、CART算法（基尼系数）。

1. ID3算法：基于"信息增益"选择特征

核心指标是"熵"和"信息增益"：

熵（Entropy）：衡量数据集"混乱程度"的指标。计算公式为：对数据集中每个标签类别的概率，取负对数后求和（公式：H = -ΣP(x)log₂P(x)）。熵值越大，说明数据中标签类别越分散，混乱程度越高；熵值越小，标签越集中，纯度越高。
信息增益（Information Gain）：衡量"用某个特征分裂后，数据混乱程度降低的幅度"。

ID3算法具体流程：

计算原始数据集的标签熵 （记为H_total），代表分裂前的整体混乱程度；（对应总体数据所有去玩和不去玩的情况，求标签熵）
对每个待选特征，根据该特征的不同取值拆分数据集为多个子集，计算每个子集的标签熵（记为H_sub），再根据子集样本数量占比，计算所有子集的"加权平均熵"（记为H_feature）；（比如雨天情况下，对所有去玩yes和不去玩No求熵，在和其他天气的熵值求平均）
计算该特征的信息增益：IG = H_total - H_feature；
选择"信息增益最大"的特征作为当前分裂节点（信息增益越大，说明用该特征分裂后，数据纯度提升越明显 ）；（比如下图阴天球的的熵值很小的，最终的信息增益就大。本质上是因为做了好的分类，阴天全为yes，表现在数学计算的熵值就是小的）
对分裂后的每个子集，重复步骤1-4，直至满足停止条件。

举例：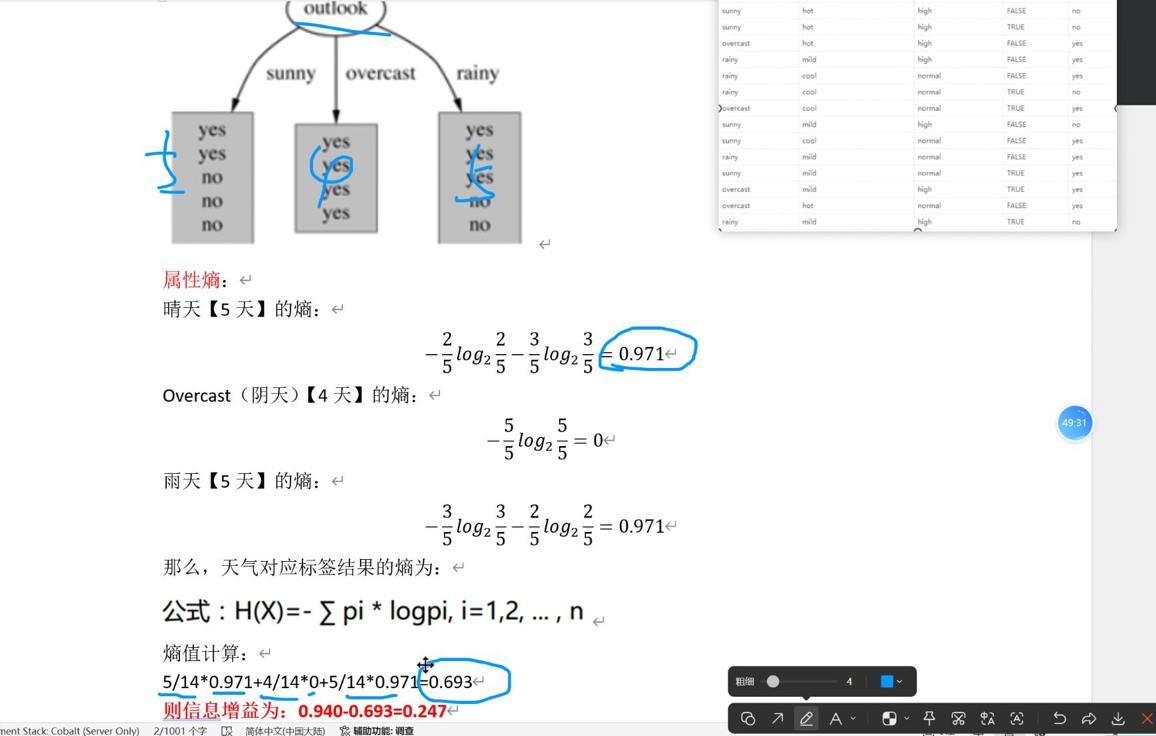

2. C4.5算法：基于"信息增益比"（ID3的优化版）

ID3算法的缺陷是"偏爱取值多的特征"（如"客户ID"这类唯一值特征，自然是好分类，分裂后熵为0，信息增益极大，但无泛化能力：我们若是选择id作为根节点，新的数据根本无法实现分类）。C4.5作为ID3的衍生版，通过"信息增益比"解决该问题：

信息增益比 = 该特征的信息增益 / 该特征自身的熵值（特征熵：衡量特征取值的混乱程度，取值越多的特征，自身熵值越大）；
算法逻辑：选择"信息增益比最大"的特征作为分裂节点。通过除以特征自身熵值，抵消了对"取值多的特征"的偏好，提升了算法的稳定性和泛化能力。

举例：

3. CART算法：基于"基尼系数"（工业界主流）

CART算法（分类与回归树）是目前应用最广的决策树算法，核心指标是"基尼系数"，计算效率比熵更高：

基尼系数定义：从数据集中随机抽取两个样本，它们属于不同类别的概率（公式：G = 1 - ΣP(x)²）；
核心逻辑：数学上可以推出：基尼系数越小，说明数据集中样本类别越集中，纯度越高；反之则越混乱。

CART算法具体流程：

对每个待选特征，计算该特征不同划分方式下（如连续特征的阈值、离散特征的取值），分裂后所有子集的"加权平均基尼系数"；
选择"加权平均基尼系数最小"的特征（及对应的划分方式）作为当前分裂节点；
对分裂后的子集重复上述步骤，直至满足停止条件（CART树默认是二叉树，无论特征是离散还是连续，均拆分为两个子集）。

举例：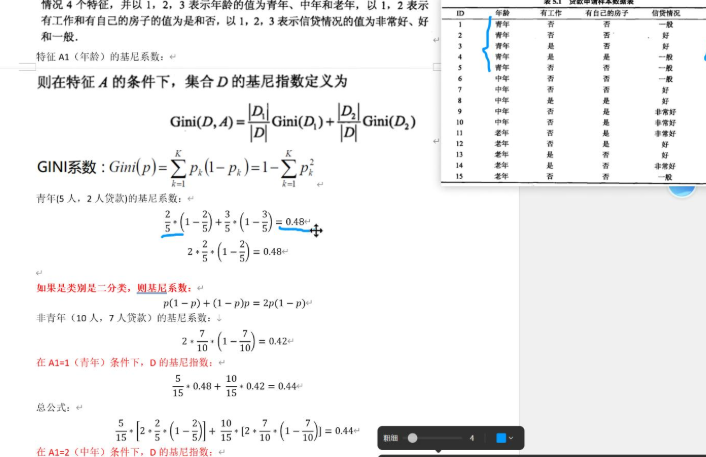

三种算法本质的原理都是使得根节点分开的两个子集纯度最高，或者说混乱程度最低，达到分类的效果。

四、决策树类的使用

举例：

python 复制代码

clf = DecisionTreeClassifier(
    criterion='gini',  # 划分准则：gini（基尼系数）/ entropy（信息熵）
    max_depth=8,  # 树的最大深度（限制树复杂度，防止过拟合）
    min_samples_split=25,  # 节点分裂所需的最小样本数
    random_state=42
)

五、决策树剪枝

我们决策是同样可能会出现过拟合的情况：每一条数据都有一条路径，但是输入新数据不存在路径。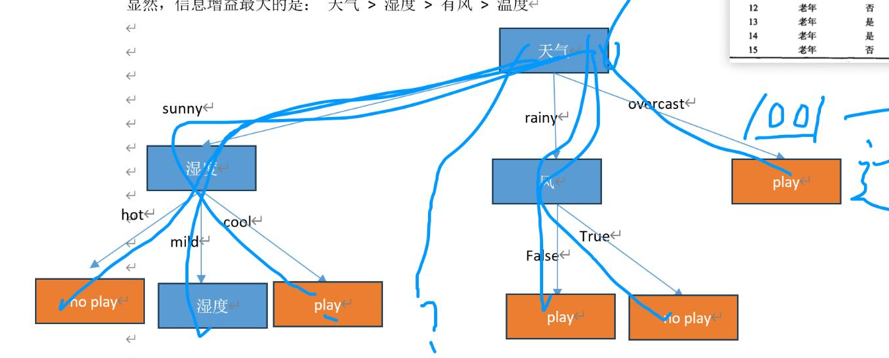

防止过拟合我们采取决策树剪枝：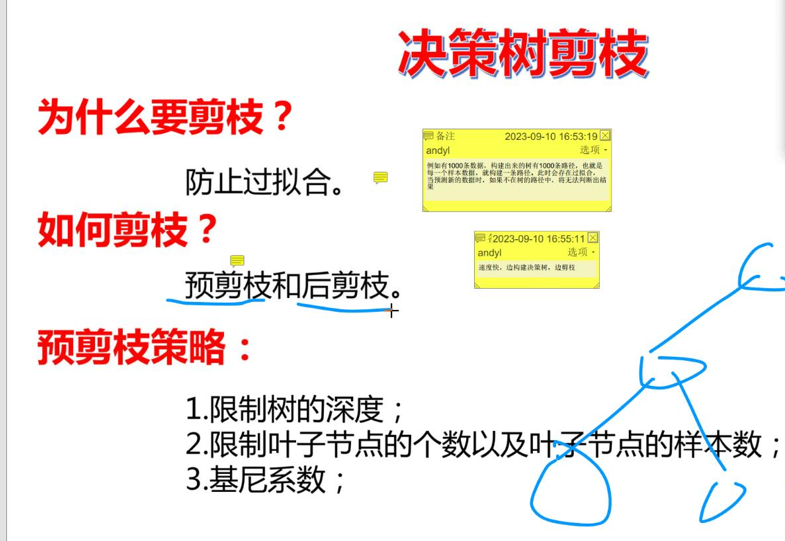

那么具体在代码中我们如何实现预剪枝呢？其实没有说明好的办法，我们采取和逻辑回归当时调整正则化因子一样的策略，循环遍历+交叉验证来寻找效果好的深度，叶子节点数以及节点的样本数等。

六、案例

我们根据信息判断客户是否流失。

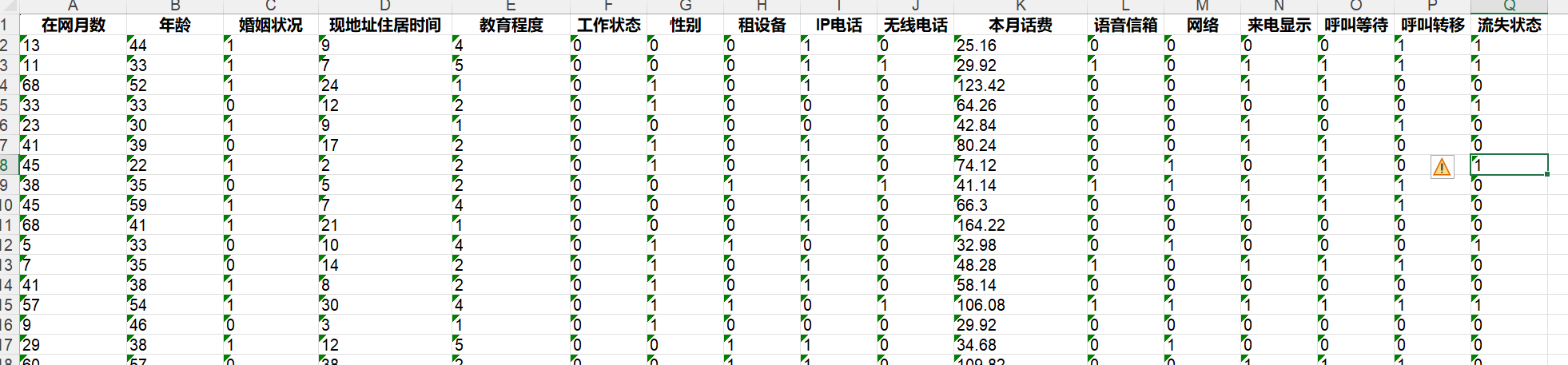
代码思路：读取数据，分割数据，（循环遍历深度，节点样本数等，交叉验证看，下面代码我没用），训练模型，预测，得分

代码：

python 复制代码

import pandas as pd

df=pd.read_excel("电信客户流失数据.xlsx")
x=df.drop("流失状态",axis=1)
y=df["流失状态"]
from sklearn.model_selection import train_test_split
X = df.drop('流失状态', axis=1)  # 特征集（二维DataFrame）
y = df['流失状态']               # 标签集（一维Series）
x_train, x_test, y_train, y_test = train_test_split(
    X,          # 特征集
    y,          # 标签集
    test_size=0.3,  # 测试集占比（如0.2表示20%测试集，80%训练集）
    random_state=40  # 随机种子（固定值可让每次切分结果一致）
)
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier(
    criterion='gini',  # 划分准则：gini（基尼系数）/ entropy（信息熵）
    max_depth=8,  # 树的最大深度（限制树复杂度，防止过拟合）
    min_samples_split=25,  # 节点分裂所需的最小样本数
    random_state=42
)


clf.fit(x_train,y_train)
train_pre=clf.predict(x_train)

test_pre=clf.predict(x_test)

from sklearn import metrics
print(metrics.classification_report(y_train, train_pre,digits=6))
cm_plot(y_train,train_pre).show()

print(metrics.classification_report(y_test, test_pre,digits=6))
cm_plot(y_test,test_pre).show()

运行结果：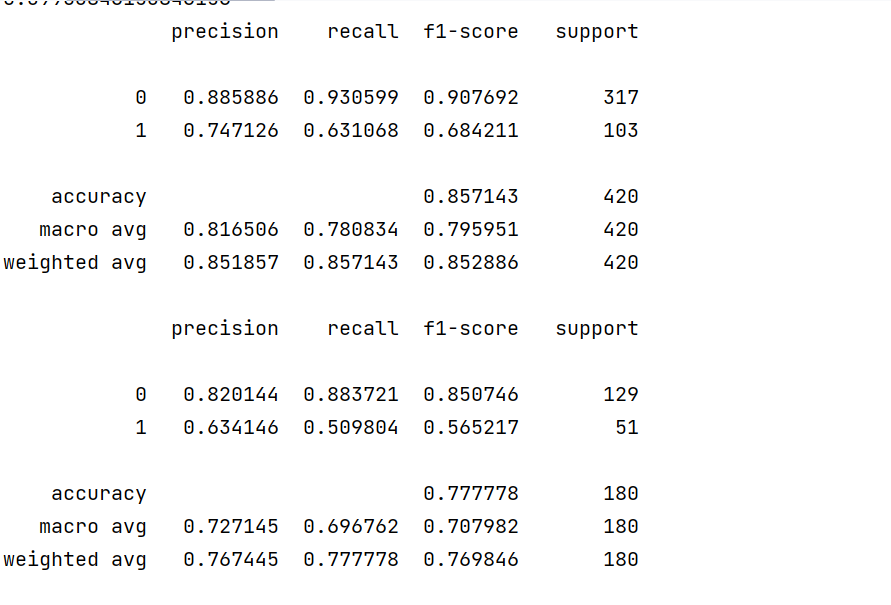

七、决策树的另一种用法：回归树模型

决策树并非只适用于分类任务，它同样可以扩展到回归场景------这就是回归树。如果说分类树是输出样本的类别，那回归树的核心是输出一个连续的数值，其思路和"近邻回归"类似，但更依赖"划分区域+区域均值"的逻辑。

回归树的核心原理

回归树的本质是：将特征空间划分为若干个互不重叠的区域，每个区域对应一个叶子节点；对任意输入样本，找到它所属的叶子节点，用该节点内所有样本的目标值（y）的平均值，作为这个样本的预测结果。

而划分特征空间的关键，是通过"最小化损失"选择最优划分点，步骤如下：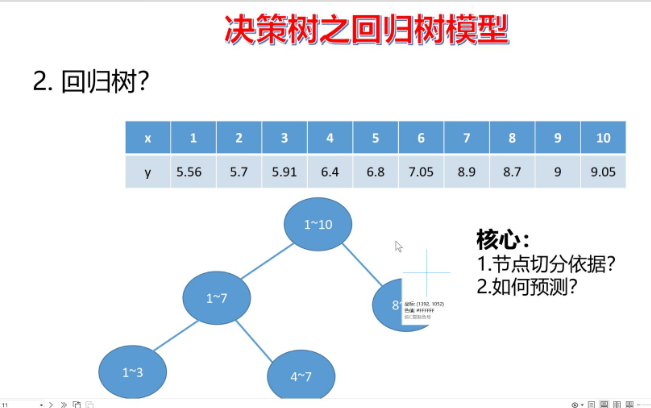

选择候选划分点：对特征x，在每两个相邻x之间取中点作为候选划分点（如1.5、2.5、3.5......9.5）。
计算损失函数 ：对每个候选划分点，将数据分为"左子集"和"右子集"，计算两个子集的平方误差和（SSE）------即"左子集y的方差×左子集样本数 + 右子集y的方差×右子集样本数"。
确定最优划分点：选择SSE最小的候选划分点，将数据拆分为两个子集；对每个子集重复上述步骤，直到满足停止条件（如划分后样本数过少），最终形成回归树。

回归树的特点

回归树的输出是一个"分段常数函数"（每个区域对应一个固定均值），它的优势是解释性强、对非线性关系的拟合更灵活 ；但缺点是预测结果不够平滑（不同区域的均值会突变），实际应用中常结合"集成学习"（如随机森林回归、梯度提升树）来提升效果。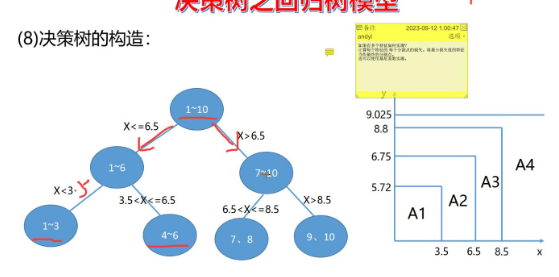

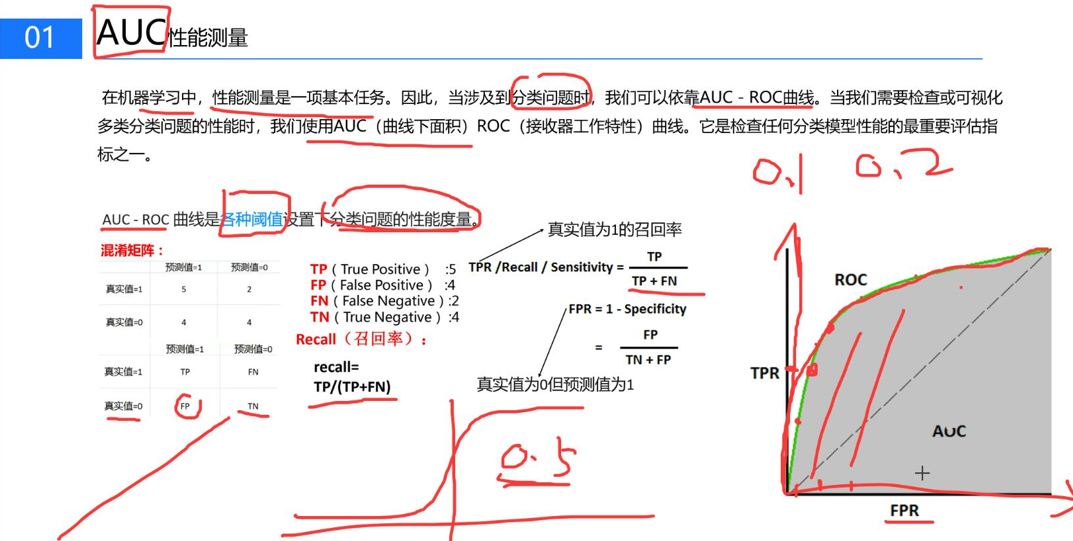
八、AUC性能测量

九、集成学习

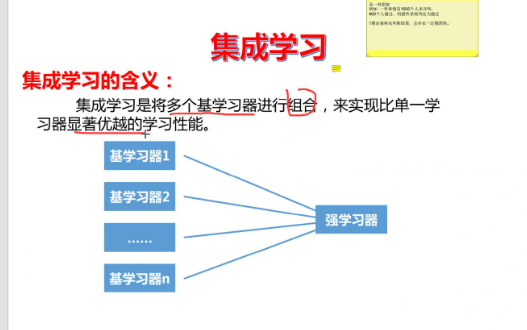
什么是集成学习呢？我们可以用一个通俗的例子理解：一个人学习后参加考试，未必能取得好成绩；但如果很多人一起学习，把大家的学习成果整合起来，就能形成更全面的知识体系。集成学习的核心原理正是如此------单个决策树可能无法很好地学习数据规律，但用一堆决策树协同工作，就能显著提升模型性能。

集成学习有三种代表性方法：

Bagging：典型应用是随机森林。它以决策树作为基础学习器，每个决策树从随机抽取的数据中选择随机的特征进行学习，多个决策树的结果整合后，能更全面地拟合整个数据集。优点：1. 泛化能力强，通过多棵树的集成有效降低了单棵决策树的过拟合风险；2. 对异常值和噪声数据有较好的鲁棒性；3. 支持并行训练，训练效率较高；4. 能评估各特征的重要性，便于特征选择。缺点：1. 模型结构复杂，解释性远不如单棵决策树清晰；2. 在处理高维稀疏数据时，性能可能不如一些专门的模型；3. 对于某些简单的线性关系数据，可能存在"欠拟合"风险，且训练和预测的内存消耗较大。
Boosting：典型应用是XGBoost。它通过迭代训练基础学习器，每次训练都会关注上一轮模型预测错误的样本，逐步修正模型偏差，提升预测准确性。
Stacking（堆叠模型）：将多个不同类型的基础学习器的预测结果作为新特征，再训练一个新的模型来进行最终预测，相当于"模型的模型"，能充分利用不同模型的优势。

下篇博客我们通过案例演示集成学习。