当信息太多时,你需要一位"智能裁缝"
想象一下,你要准备一次重要的旅行,行李箱的空间有限,但面前摊开了几十件衣服。每件衣服你都想带,但箱子装不下。这时候你需要做选择:留下最必要、最百搭的那几件,其他的暂时放下。这个选择过程,不就是我们生活中常遇到的"取舍"吗?
在人工智能的世界里,尤其是当我们用数据做预测的时候,会遇到一模一样的问题。假设你想预测房价,可能有100个影响因素:面积、朝向、楼层、学区、附近超市数量、社区绿化率、装修年份......甚至还有"前房主星座"这种可能没什么用的信息。
问题来了:如何从这100个因素中,找出真正影响房价的那几个关键因素?如果全部考虑进去,模型会变得复杂、难理解,还可能被无用信息"带偏"。
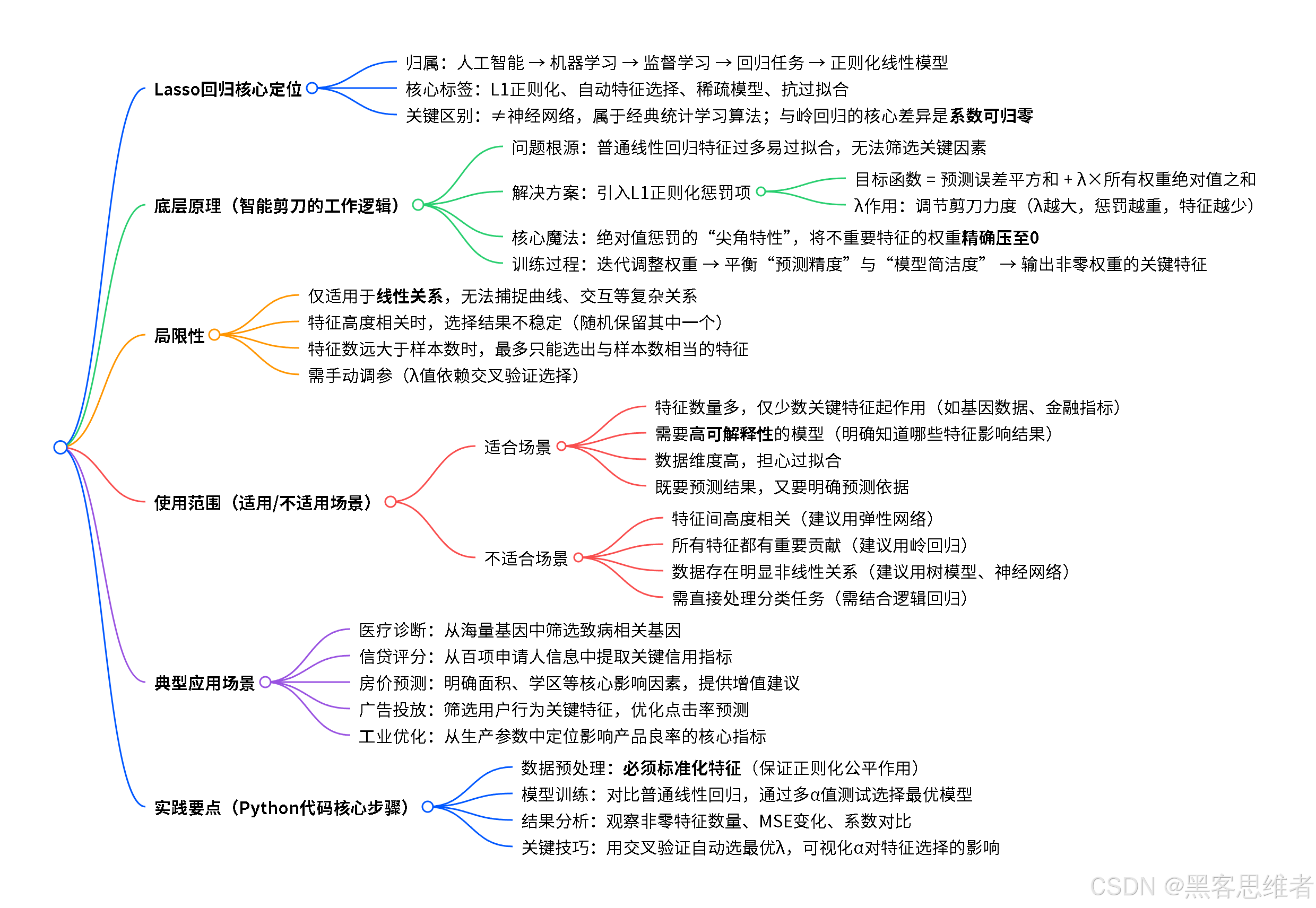
今天我要给你介绍的Lasso回归算法 ,就是一把"智能剪刀",一个"魔法裁缝"。它的绝活是:在做预测的同时,自动帮我们识别并保留最重要的特征,把不那么重要的特征的"发言权"降到零。
更重要的是,它不是神经网络 。这点很重要!它属于更传统、更基础的机器学习算法,但却是理解许多更复杂模型(包括某些神经网络正则化技术)的绝佳起点。让我们一起来认识这位"智能剪刀手"吧!
一、分类归属:Lasso在AI大家庭中的位置
为了让Lasso回归找到自己的"座位",我们先来看看AI大家庭的"家族树":
人工智能 机器学习 其他AI分支
如专家系统 监督学习 无监督学习 强化学习 分类任务
如判断猫狗 回归任务
如预测房价 线性回归
所有特征都参与 正则化回归
约束特征数量/权重 Lasso回归
L1正则化 Ridge回归
L2正则化 弹性网络
L1+L2结合
现在,我们来给Lasso回归贴几个标签:
-
从学习方式看 :它是监督学习算法。这意味着它需要"标准答案"来学习。就像学生做题需要参考答案一样,Lasso需要已知的"输入-输出"配对数据(比如已知的房价和对应的各种特征)来训练自己。
-
从任务类型看 :它是回归算法 。回归任务的核心是预测一个连续值。房价(比如356.7万)、明天气温(比如23.5℃)、销售额(比如128.4万元)这些都是连续值,适合用回归来预测。如果是判断"这是猫还是狗""邮件是垃圾邮件吗",那就是分类任务,需要别的算法。
-
从模型特点看 :它是线性模型 + L1正则化。这是它最核心的身份标识!
- 线性:它假设特征和目标值之间的关系大致是"直线关系"。比如面积每增加1平米,房价增加固定金额。
- L1正则化:这是它的"魔法剪刀"。正则化就像是给模型"立规矩",防止它太复杂、太依赖数据细节。L1是其中一种"规矩",效果特别像一把精准的剪刀,能把不重要的特征的系数直接剪到零。
简单来说 :Lasso回归是机器学习 中的一种监督式线性回归模型 ,它的独门绝技是自动进行特征选择,在预测的同时找出最关键的几个因素。
关键点:很多初学者会混淆神经网络和传统机器学习算法。你可以这样记:神经网络通常结构更复杂、层数更深,像人脑的简化模拟;而Lasso回归这类算法更"数学化"、结构更简单透明,是解决许多实际问题的快速有效工具。两者都是AI工具箱里的重要成员。
二、底层原理:Lasso的"魔法剪刀"是如何工作的?
第一步:先认识普通的线性回归(没有剪刀的裁缝)
想象一个简单的场景:只用"房屋面积"来预测"房价"。
普通线性回归的做法是:找一条直线,让这条直线尽可能地穿过所有数据点。这条直线的方程是:
房价=w×面积+b房价 = w \times 面积 + b房价=w×面积+b
这里:
- ( w ) 是权重(斜率),表示面积每增加1平米,房价增加多少万
- ( b ) 是偏置(截距),可以理解为"基础房价"
如果有多个特征(面积、楼层、朝向......),方程就变成:
房价=w1×面积+w2×楼层+w3×朝向+...+b房价 = w_1 \times 面积 + w_2 \times 楼层 + w_3 \times 朝向 + ... + b房价=w1×面积+w2×楼层+w3×朝向+...+b
普通线性回归的目标 :找到一组 ( w_1, w_2, w_3, ... ) 和 ( b ),让模型预测的房价和真实房价之间的总误差最小。
第二步:问题来了------过拟合(裁缝太听顾客的话)
假设我们数据中有"前房主星座"这个特征。普通线性回归会诚实地给这个特征分配一个权重 ( w_{星座} )。哪怕星座和房价其实没关系,模型也会努力从训练数据中找到某种(可能是偶然的)关联,把这个权重调来调去。
结果呢?模型在训练数据 上表现很好(因为它连"星座"这种噪音都考虑进去了),但拿到新数据上预测时,效果很差。这就是过拟合:模型太复杂,记住了训练数据的细节(包括噪音),而没学会真正的规律。
第三步:Lasso的解决方案------给裁缝一把"预算剪刀"
Lasso回归的想法很巧妙:我们不仅要预测得准,还要让模型"简洁"。
怎么实现"简洁"?它修改了训练目标:
新目标=最小化(预测误差+λ×所有权重的绝对值之和)新目标 = 最小化(预测误差 + λ × 所有权重的绝对值之和)新目标=最小化(预测误差+λ×所有权重的绝对值之和)
用公式表示就是:
min{∑i=1n(yi−y^i)2+λ∑j=1p∣wj∣}\min \left\{ \sum_{i=1}^{n}(y_i - \hat{y}i)^2 + \lambda \sum{j=1}^{p}|w_j| \right\}min{i=1∑n(yi−y^i)2+λj=1∑p∣wj∣}
别怕这个公式,我们拆开看:
- 左边部分 ∑(yi−y^i)2 \sum (y_i - \hat{y}_i)^2∑(yi−y^i)2:就是原来的目标,让预测误差小
- 右边部分 λ∑∣wj∣\lambda \sum |w_j|λ∑∣wj∣:这是新加的规矩,惩罚大的权重
- λ(读作"拉姆达"):平衡剪刀的"力度"。λ越大,惩罚越重,模型越简洁
第四步:"绝对值惩罚"的魔法(剪刀如何工作?)
关键就在于这个"绝对值之和"的惩罚。它有一个神奇的特性:倾向于把一些不重要的特征的权重直接推到零。
生活化比喻 :
想象你有1000元预算,要给不同的朋友买礼物。有些朋友很重要(关键特征),你会多花点钱(大权重);有些朋友关系一般(次要特征),你少花点;还有些只是点头之交(无用特征),你干脆不买礼物了(权重为零)。
Lasso的"绝对值惩罚"就像这个预算约束:
- 如果你给某个朋友(特征)买了很贵的礼物(权重很大),就会花掉很多预算
- 为了在总预算(惩罚项)有限的情况下,还能给重要的朋友买好礼物,你会选择完全不送给一些不重要的朋友(把他们的权重设为零)
- 这样,最后真正收到礼物的(权重非零的)只有最重要的那几个朋友(特征)
技术上说 :绝对值函数在零点处是"尖"的,不像平方函数那么"圆滑"。这个数学特性导致在优化过程中,许多权重会精确地变为零。这是Lasso和Ridge回归(用平方惩罚)的主要区别------Ridge只会把权重变小,但很少变为零。
第五步:Lasso的训练过程(裁缝如何使用剪刀?)
是 否 输入数据 初始化权重 计算预测值 计算误差 计算目标函数 调整权重 继续? 更新权重 输出结果
通俗解释这个过程:
- 开始时,Lasso像普通线性回归一样,给所有特征分配初始权重
- 然后它开始"试错调整":微调每个权重,看调整后总目标函数(误差+惩罚)是变大了还是变小了
- 调整时它面临"权衡":
- 如果把某个特征的权重调大,可能让预测更准(误差变小),但会增大惩罚项
- 如果把权重调小,惩罚项变小了,但可能让预测误差变大
- 经过反复调整,最终达到平衡:重要的特征保留合适的权重,不重要的特征的权重被压到零
- 训练完成!我们不仅得到了预测模型,还知道了哪些特征是真正重要的
核心要点 :Lasso通过"误差 + 惩罚"的双目标优化,同时完成了两件事:(1)学习预测规律;(2)自动选择特征。这是它最强大的地方!
三、局限性:魔法剪刀也有剪不到的时候
没有完美的算法,Lasso回归也不例外。了解它的局限,你才能知道什么时候该用它,什么时候该换工具。
局限性1:它假设线性关系(只认识直线世界)
问题 :Lasso是线性模型,它只能捕捉特征和目标之间的线性关系。
例子:如果房价和面积的真实关系是曲线------面积很小或很大时,单价会变化------Lasso只能用一条直线去近似,效果就不会太好。
为什么有这个局限:因为它的基本形式就是加权求和。就像你用不同颜色的画笔(特征)画画,但只能简单叠加,不能混合出全新的颜色或画弯曲的线条。
应对方法:对于非线性问题,可以:
- 先对特征进行变换(比如把面积取平方、取对数作为新特征)
- 使用能处理非线性的模型(如决策树、神经网络)
局限性2:特征高度相关时选择不稳定(剪刀犹豫不决)
问题:当两个特征高度相关时(比如"建筑面积"和"使用面积"),Lasso可能随机选择其中一个,或者两者权重都不够大。
例子:你想预测跑步速度,既有"步频"也有"步幅"数据。这两个高度相关(通常步频大步幅小,或反之)。Lasso可能只选了步频,把步幅的权重压到零,但实际两者都重要。
为什么有这个局限:数学上,当两个特征提供几乎相同的信息时,惩罚项"无所谓"选哪个。就像你有两把功能几乎一样的剪刀,Lasso可能随便拿一把用。
应对方法:
- 先用专业知识判断,如果确实都重要,就不要用Lasso做特征选择
- 使用弹性网络(Elastic Net),它结合了Lasso和Ridge的优点,能更好地处理相关特征
局限性3:特征数远大于样本数时的限制(小剪刀对大布料)
问题:当特征数量§远远大于样本数量(n)时(比如基因数据:几万个基因,只有几百个病人),Lasso最多只能选出n个非零特征。
为什么有这个局限:这是数学上的硬性限制。想象你有100个朋友(样本),但想从1000件礼物(特征)中选。Lasso的"预算剪刀"最多只能让你买100份不同的礼物,因为每份礼物至少对应一个朋友。
应对方法:这种情况下可能需要:
- 先进行预筛选,减少特征数量
- 使用专门处理高维数据的方法
局限性4:需要手动调节λ(剪刀力度不好把握)
问题:λ这个超参数需要人为设定或通过交叉验证选择。选得太小,惩罚不够,模型还是复杂;选得太大,惩罚过重,可能把重要特征也剪掉了。
为什么:这是所有正则化方法的共同挑战。没有一个"放之四海而皆准"的λ值,需要根据具体数据和问题调整。
好消息:实践中我们可以用交叉验证自动选择较优的λ值,虽然不是完全自动,但已经大大简化了工作。
重要心态:认识到算法的局限不是否定它,而是为了更好地使用它。就像你知道剪刀不能切菜,就不会用它切菜,但裁衣服时它仍是最好用的工具之一。
四、使用范围:什么样的问题适合请出这位"智能裁缝"?
适合使用Lasso的场景:
-
特征数量多,但你认为只有少数真正重要
- 典型例子:基因数据分析(几万个基因,可能只有几十个与某疾病相关)
- 金融风险预测(几百个经济指标,少数几个是关键领先指标)
- 文本分类(词汇表很大,但只有部分词汇对分类有帮助)
-
你需要可解释的模型
- Lasso最终只会保留少数特征,模型简单,容易解释
- 你可以明确说:"我们的模型发现,影响房价的只有面积、地段、学区这三个因素"
-
你既要预测,又要知道"为什么"
- 很多场景下,我们不仅想知道预测结果,还想知道依据是什么
- 比如医疗诊断:不仅要预测是否患病,还要知道是哪些指标异常导致了预测
-
数据维度高,担心过拟合
- 当特征数接近甚至多于样本数时,普通线性回归极易过拟合
- Lasso的正则化能有效控制模型复杂度,提高泛化能力
不适合使用Lasso的场景:
-
特征之间高度相关
- 如前面所说,Lasso在这种情况下选择不稳定
-
所有特征都可能重要,你不想做特征选择
- 如果你从专业知识知道,所有特征都有贡献,只是程度不同
- 这时用Ridge回归可能更合适(它缩小所有权重但不压到零)
-
明确知道关系是非线性的
- 如果特征和目标之间是复杂的曲线关系、交互关系
- 考虑决策树、随机森林、神经网络等非线性模型
-
需要预测概率的分类问题
- Lasso是回归算法,虽然可以通过逻辑回归+L1正则化做分类,但那是它的"变体"
- 对于多分类、概率预测等,有更专门的分类算法
简单判断流程:
问题类型? → 如果是回归或二分类(可套逻辑回归) → 特征是否很多? → 是 → 是否需要特征选择? → 是 → 特征是否高度相关? → 否 → ✅ 适合Lasso
↓
是 → 考虑弹性网络五、应用场景:Lasso在真实世界中的魔法时刻
案例1:医疗诊断助手------从海量基因中找出致病基因
场景:研究人员有1000名癌症患者和健康人的基因数据,每个人的基因测序结果包含2万多个基因表达值。他们想找出哪些基因与这种癌症最相关。
Lasso的作用:
- 把"是否患癌"作为目标变量(0=健康,1=患病)
- 把2万个基因的表达值作为特征
- Lasso会从中自动筛选出可能只有几十个的关键基因
- 结果:不仅建立了预测模型,还为生物学家提供了研究方向------"这几十个基因值得深入研究"
价值:大大缩小研究范围,节省大量实验成本和时间。
案例2:智能信贷评分------找出最关键的信用指标
场景:银行想建立自动化信贷审批模型。他们收集了申请人100多个信息:年龄、收入、职业、教育、过往信用记录、消费习惯、社交媒体数据......
Lasso的作用:
- 把"是否违约"作为目标
- 100多个特征作为输入
- Lasso从中选出10-15个最相关的特征,比如:过去两年逾期次数、收入负债比、当前工作持续时间
- 银行得到了一个既准确又可解释的模型:"我们的审批主要看这10个指标"
价值:符合监管要求(模型可解释),同时自动化处理,提高效率。
案例3:房价预测平台------告诉用户什么最影响房价
场景:房产平台想给用户提供房价评估功能,同时告诉用户:"你的房子如果改进X,能增值多少"。
Lasso的作用:
- 收集海量成交数据:面积、楼层、朝向、装修、学区、交通......
- 使用Lasso回归预测房价
- 发现最终只有7个特征权重非零:面积、地段评分、学区评分、房龄、地铁距离、商业配套、小区绿化率
- 平台可以明确告诉用户:"根据我们的模型,影响房价的主要是这7个因素"
价值:不仅提供估价,还提供改进建议,增加用户粘性。
案例4:广告点击率预测------从用户行为中找关键信号
场景:电商平台想预测用户是否会点击某个广告。有上千个可能的特征:用户历史浏览记录、购买记录、时间、设备、广告内容、促销信息......
Lasso的作用:
- 筛选出真正影响点击率的少数特征
- 比如:用户过去7天搜索过该品类、广告位在首页前三屏、有"限时优惠"标签
- 平台可以优化广告投放:优先展示给有这些特征的用户
价值:提高广告效率,减少用户打扰,增加平台收入。
案例5:工业生产优化------找出影响产品质量的关键参数
场景:芯片制造厂,生产过程中有200多个可控参数(温度、压力、时间、化学浓度......)。想找出哪些参数对最终芯片良率影响最大。
Lasso的作用:
- 以"芯片良率"为目标,200多个生产参数为特征
- 筛选出10个关键参数
- 工程师可以重点关注这10个参数的调控,简化生产控制复杂度
价值:提高生产效率,降低次品率,减少控制复杂度。
六、动手实践:用Python实现Lasso房价预测
让我们通过一个简单的例子,看看Lasso在实际代码中如何工作。
python
# -*- coding: utf-8 -*-
"""
Lasso回归实战:波士顿房价预测
适合初学者的完整示例
"""
# 1. 导入必要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso, LinearRegression
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_squared_error, r2_score
# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
print("=" * 60)
print("Lasso回归实战:加州房价预测")
print("=" * 60)
# 2. 加载数据
print("\n1. 加载加州房价数据集...")
housing = fetch_california_housing()
X = housing.data # 特征数据
y = housing.target # 目标值:房价中位数(单位:10万美元)
feature_names = housing.feature_names
print(f"数据集形状:{X.shape}")
print(f"特征数:{X.shape[1]}")
print(f"样本数:{X.shape[0]}")
print(f"\n特征名称:")
for i, name in enumerate(feature_names):
print(f" {i+1}. {name}")
print(f"\n目标变量:房价中位数(单位:10万美元)")
print(f"房价范围:${y.min():.2f}万 到 ${y.max():.2f}万")
# 3. 数据预处理
print("\n2. 数据预处理...")
# 标准化特征(对Lasso很重要,因为惩罚项对尺度敏感)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
X_scaled, y, test_size=0.2, random_state=42
)
print(f"训练集大小:{X_train.shape[0]} 个样本")
print(f"测试集大小:{X_test.shape[0]} 个样本")
# 4. 训练普通线性回归作为对比
print("\n3. 训练普通线性回归作为基准...")
lr = LinearRegression()
lr.fit(X_train, y_train)
# 训练Lasso回归
print("4. 训练Lasso回归...")
# 尝试不同的λ值(在sklearn中参数是alpha,相当于λ)
alphas = [0.001, 0.01, 0.1, 1, 10]
results = []
for alpha in alphas:
lasso = Lasso(alpha=alpha, max_iter=10000, random_state=42)
lasso.fit(X_train, y_train)
# 预测
y_pred_train = lasso.predict(X_train)
y_pred_test = lasso.predict(X_test)
# 评估
train_mse = mean_squared_error(y_train, y_pred_train)
test_mse = mean_squared_error(y_test, y_pred_test)
train_r2 = r2_score(y_train, y_pred_train)
test_r2 = r2_score(y_test, y_pred_test)
# 统计非零权重的数量
non_zero_count = np.sum(lasso.coef_ != 0)
results.append({
'alpha': alpha,
'non_zero_features': non_zero_count,
'train_mse': train_mse,
'test_mse': test_mse,
'train_r2': train_r2,
'test_r2': test_r2,
'model': lasso
})
print(f"\n alpha={alpha}:")
print(f" 非零特征数:{non_zero_count}/{X.shape[1]}")
print(f" 训练集R²:{train_r2:.4f},测试集R²:{test_r2:.4f}")
# 5. 选择最佳模型
print("\n5. 分析结果...")
best_result = min(results, key=lambda x: x['test_mse'])
best_lasso = best_result['model']
print(f"\n最佳模型:alpha={best_result['alpha']}")
print(f"测试集MSE最低:{best_result['test_mse']:.4f}")
print(f"保留的特征数:{best_result['non_zero_features']}个")
# 6. 比较Lasso和普通线性回归
print("\n6. Lasso vs 普通线性回归 对比:")
# 普通线性回归的评估
y_pred_lr_test = lr.predict(X_test)
lr_test_mse = mean_squared_error(y_test, y_pred_lr_test)
lr_test_r2 = r2_score(y_test, y_pred_lr_test)
print(f"\n普通线性回归:")
print(f" 测试集MSE:{lr_test_mse:.4f}")
print(f" 测试集R²:{lr_test_r2:.4f}")
print(f" 使用的特征数:{X.shape[1]}个(全部)")
print(f"\nLasso回归(alpha={best_result['alpha']}):")
print(f" 测试集MSE:{best_result['test_mse']:.4f}")
print(f" 测试集R²:{best_result['test_r2']:.4f}")
print(f" 使用的特征数:{best_result['non_zero_features']}个")
if best_result['test_mse'] < lr_test_mse:
print("\n✅ Lasso表现优于普通线性回归!")
print(" 说明特征选择帮助提高了泛化能力")
else:
print("\n⚠️ 普通线性回归表现略好")
print(" 可能α选择不是最优,或者所有特征都重要")
# 7. 可视化结果
print("\n7. 可视化分析...")
# 创建可视化
fig, axes = plt.subplots(2, 2, figsize=(14, 10))
# 子图1:不同alpha的效果
axes[0, 0].plot([r['alpha'] for r in results], [r['test_mse'] for r in results],
'bo-', linewidth=2, markersize=8, label='测试集MSE')
axes[0, 0].plot([r['alpha'] for r in results], [r['train_mse'] for r in results],
'ro--', linewidth=2, markersize=8, label='训练集MSE')
axes[0, 0].set_xscale('log')
axes[0, 0].set_xlabel('正则化强度 α(log尺度)', fontsize=12)
axes[0, 0].set_ylabel('均方误差 (MSE)', fontsize=12)
axes[0, 0].set_title('不同α值对模型性能的影响', fontsize=14, fontweight='bold')
axes[0, 0].legend()
axes[0, 0].grid(True, alpha=0.3)
# 子图2:非零特征数随alpha变化
axes[0, 1].plot([r['alpha'] for r in results], [r['non_zero_features'] for r in results],
'go-', linewidth=2, markersize=10)
axes[0, 1].set_xscale('log')
axes[0, 1].set_xlabel('正则化强度 α(log尺度)', fontsize=12)
axes[0, 1].set_ylabel('非零特征数量', fontsize=12)
axes[0, 1].set_title('特征选择效果:α越大,保留特征越少', fontsize=14, fontweight='bold')
axes[0, 1].grid(True, alpha=0.3)
# 标记每个点
for i, r in enumerate(results):
axes[0, 1].annotate(f"{r['non_zero_features']}",
xy=(r['alpha'], r['non_zero_features']),
xytext=(5, 5), textcoords='offset points')
# 子图3:Lasso系数与线性回归系数对比
x_pos = np.arange(len(feature_names))
width = 0.35
axes[1, 0].bar(x_pos - width/2, lr.coef_, width, label='线性回归', alpha=0.7)
axes[1, 0].bar(x_pos + width/2, best_lasso.coef_, width, label=f'Lasso (α={best_result["alpha"]})', alpha=0.7)
axes[1, 0].set_xlabel('特征', fontsize=12)
axes[1, 0].set_ylabel('系数值', fontsize=12)
axes[1, 0].set_title('特征权重对比:Lasso使不重要的特征权重为0', fontsize=14, fontweight='bold')
axes[1, 0].set_xticks(x_pos)
axes[1, 0].set_xticklabels(feature_names, rotation=45, ha='right')
axes[1, 0].legend()
axes[1, 0].grid(True, alpha=0.3, axis='y')
# 子图4:预测 vs 实际值
axes[1, 1].scatter(y_test, best_lasso.predict(X_test), alpha=0.6)
axes[1, 1].plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()],
'r--', linewidth=2, label='理想预测线')
axes[1, 1].set_xlabel('实际房价(10万美元)', fontsize=12)
axes[1, 1].set_ylabel('预测房价(10万美元)', fontsize=12)
axes[1, 1].set_title('Lasso预测效果', fontsize=14, fontweight='bold')
axes[1, 1].legend()
axes[1, 1].grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('lasso_demo_results.png', dpi=150, bbox_inches='tight')
print(" 图表已保存为 'lasso_demo_results.png'")
# 8. 展示重要特征
print("\n8. Lasso选出的重要特征:")
print("-" * 50)
# 获取非零系数的特征
non_zero_indices = np.where(best_lasso.coef_ != 0)[0]
print(f"Lasso保留了 {len(non_zero_indices)} 个重要特征:\n")
feature_importance = []
for idx in non_zero_indices:
feature_importance.append({
'特征': feature_names[idx],
'Lasso权重': best_lasso.coef_[idx],
'线性回归权重': lr.coef_[idx],
'权重绝对值': abs(best_lasso.coef_[idx])
})
# 按重要性排序
feature_importance.sort(key=lambda x: x['权重绝对值'], reverse=True)
print(f"{'特征名称':<15} {'Lasso权重':<12} {'线性回归权重':<15} {'重要性排名':<12}")
print("-" * 60)
for i, feat in enumerate(feature_importance):
print(f"{feat['特征']:<15} {feat['Lasso权重']:<12.4f} {feat['线性回归权重']:<15.4f} 第{i+1}名")
print("\n" + "=" * 60)
print("实践总结:")
print("=" * 60)
print("""
1. Lasso成功地将特征从8个减少到了{}个
2. 最重要的特征是:{}
3. Lasso的测试集R²为:{:.4f},与线性回归的{:.4f}相比{}
4. 通过调整α,我们控制了模型的复杂度和特征选择强度
通过这个例子,你可以看到Lasso如何:
✓ 自动选择重要特征
✓ 防止过拟合(当特征多时效果更明显)
✓ 产生更简单、更可解释的模型
""".format(
len(non_zero_indices),
feature_importance[0]['特征'] if feature_importance else "无",
best_result['test_r2'],
lr_test_r2,
"更好" if best_result['test_r2'] > lr_test_r2 else "稍差"
))
# 9. 扩展练习建议
print("\n" + "=" * 60)
print("扩展练习建议:")
print("=" * 60)
print("""
1. 尝试不同的α值,观察特征选择如何变化
2. 修改代码使用Ridge回归,比较L1和L2正则化的区别
3. 添加一些随机噪声特征,观察Lasso如何将其权重压到0
4. 尝试使用交叉验证自动选择最佳α值
""")
plt.show()代码运行说明:
-
安装必要库(如果你还没安装):
pip install numpy pandas matplotlib scikit-learn -
代码做了什么:
- 加载加州房价数据集
- 比较普通线性回归和Lasso回归
- 展示Lasso如何选择特征(将不重要的特征权重设为零)
- 可视化不同正则化强度(α)的影响
- 分析哪些特征对房价预测最重要
-
关键观察点:
- 当α增大时,保留的特征数减少
- Lasso的系数比线性回归的更稀疏(更多零值)
- 适当的正则化可以提高模型在测试集上的表现
总结:Lasso回归的核心价值
让我们用一句话总结Lasso回归:
Lasso回归是一把"智能剪刀",在建立预测模型的同时,自动剪掉不重要的特征,帮助我们得到更简洁、更可解释、且泛化能力更好的模型。
对于初学者来说,理解Lasso的关键在于把握三个要点:
- 双重目标:既要预测准确,又要模型简洁
- 魔法剪刀:通过L1正则化(绝对值惩罚)将不重要特征的权重精确剪到零
- 平衡艺术:通过调节λ(alpha)在"预测精度"和"模型简洁度"间找到最佳平衡
在AI学习道路上,Lasso回归是一个重要的里程碑。它展示了如何通过巧妙的数学设计,让模型既智能又简洁。掌握了Lasso,你不仅学会了一个实用工具,更理解了"正则化"这一机器学习核心思想,这将为你学习更复杂的模型(包括神经网络的Dropout、权重衰减等技术)打下坚实的基础。