从猜咖啡温度开始的故事
想象一下这个场景:你早上买了一杯热咖啡,放在桌上。你很想知道,再过15分钟,这杯咖啡会凉到多少度?
你可能会观察:
- 刚买来时:85℃
- 5分钟后:75℃
- 10分钟后:65℃
现在我问你:15分钟后会是几度?
如果你的答案是"55℃",恭喜你!你已经有了线性思维------你发现温度差不多每分钟下降2℃。但现实是,咖啡降温的速度其实会变化:一开始很快,后来变慢,最后接近室温就不再降了。如果你只用直线(线性)去猜,最后可能误差很大。
这时候,多项式回归 就登场了!它就像是更聪明的"猜温高手",不仅能看出直线趋势,还能看出曲线变化,让你更准确地预测未来。
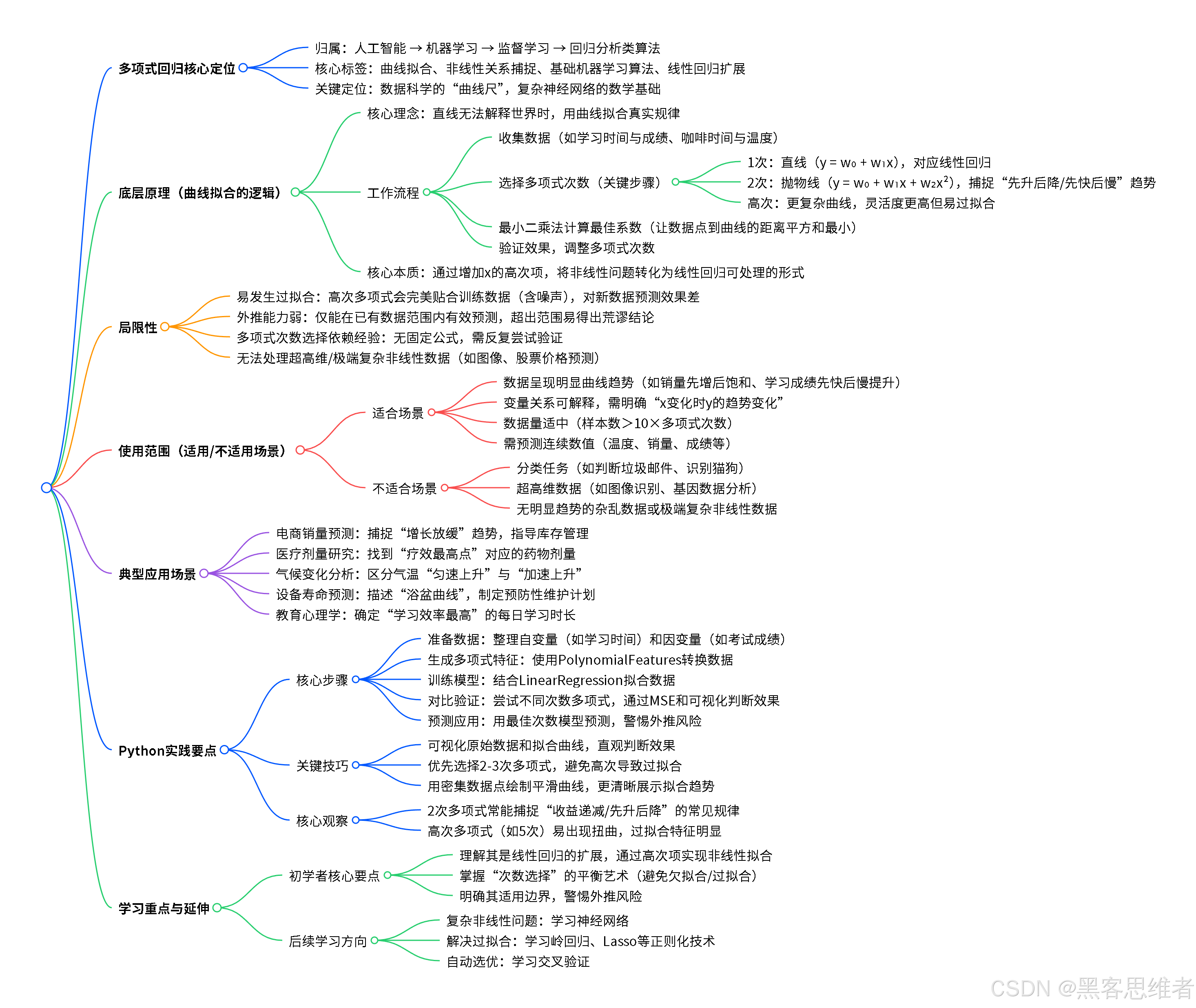
一、分类归属:它在人工智能大家庭中的位置
它是谁的孩子?
如果我们把人工智能算法看作一个大家族,多项式回归属于:
- 按功能用途划分 :回归分析类算法(专门预测连续数值,如温度、价格、销量)
- 按复杂度划分 :基础机器学习算法(比深度学习简单,但很多复杂网络的基础)
- 按关系类型划分 :曲线拟合算法(能找到数据间的非线性关系)
简单说:它是从最简单的"直线拟合"升级而来的"曲线拟合器",是很多复杂神经网络(特别是处理非线性问题的网络)的数学基础。
二、底层原理:拆解这个"曲线拟合器"
类比:从"只会画直线"到"会画曲线"的画家
想象有两位画家要描摹山丘的轮廓:
- 线性回归画家:只带了一把直尺,只能画直线 → 结果山丘被画成了三角形
- 多项式回归画家 :带了一套可弯曲的曲线尺,可以画出各种弧度的曲线 → 能更好地拟合真实山丘
核心设计理念:
"当直线解释不了世界时,我们就需要曲线。"
它是怎么工作的?
让我们用咖啡降温的例子,一步步拆解:
第一步:数据收集
时间(x): 0分钟 5分钟 10分钟
温度(y): 85℃ 75℃ 65℃第二步:选择"弯曲程度"(多项式的次数)
这是最关键的步骤!就像选择曲线尺的弯曲能力:
-
1次多项式:就是直线 y = a + bx
温度 = 初始温度 + 每分钟下降量 × 时间 -
2次多项式:抛物线 y = a + bx + cx²
温度 = 初始温度 + 下降速度项 + 加速度项 (可以描述"越降越慢"的现象) -
3次多项式:更复杂的曲线 y = a + bx + cx² + dx³
能描述"先快后慢再快"的复杂变化
次数越高,曲线越灵活,但也可能"过度弯曲"------这个我们后面会讲。
第三步:用文字描述核心逻辑
是 否 收集数据 选择多项式次数 计算最佳系数 验证曲线效果 效果好吗? 使用模型预测
关键环节解释:
- "计算最佳系数":就是调整a、b、c这些数字,让曲线尽可能贴近所有数据点
- "验证效果":用没见过的数据测试,看预测准不准
第四步:数学公式展示(了解即可)
如果你好奇它的数学形式:
一次多项式(线性):
y = w 0 + w 1 x y = w₀ + w₁x y=w0+w1x
w₀:截距(起始值),w₁:斜率(变化速度)
二次多项式:
y = w 0 + w 1 x + w 2 x 2 y = w₀ + w₁x + w₂x² y=w0+w1x+w2x2
多了x²项,可以描述加速度变化
n次多项式:
y = w 0 + w 1 x + w 2 x 2 + . . . + w n x n y = w₀ + w₁x + w₂x² + ... + wₙxⁿ y=w0+w1x+w2x2+...+wnxn
这些系数怎么求?
核心是"最小二乘法"------找一条曲线,让所有数据点到这条曲线的垂直距离的平方和最小。
就像你玩"套圈圈"游戏,目标是把所有柱子都尽可能套进圈里,多项式回归就是调整圈的大小和形状,让每个柱子离圈的距离总和最小。
三、局限性:它也不是万能的
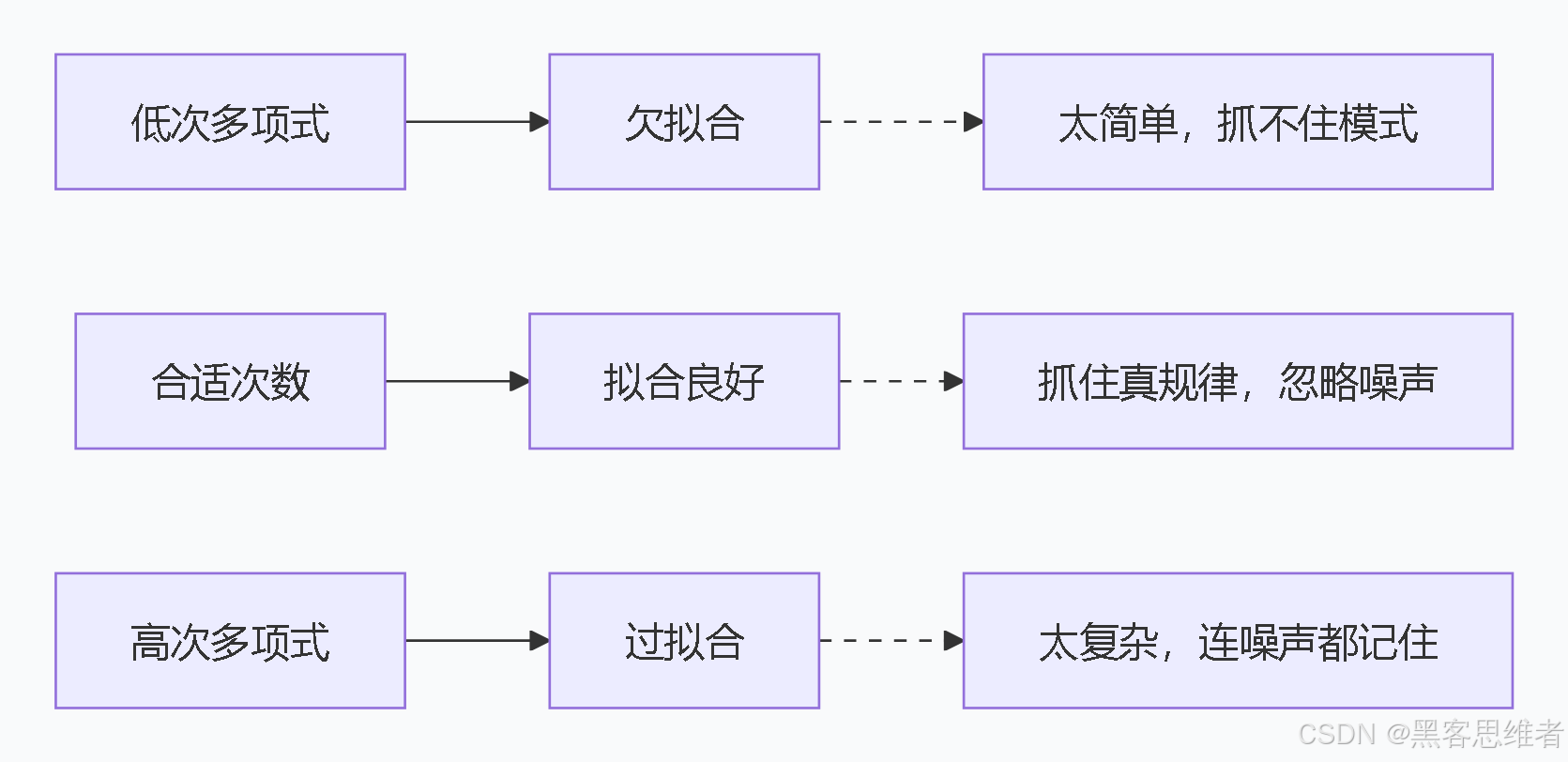
问题1:容易"过度拟合"------画蛇添足
生活类比:
你背英语单词,为了记住"apple-苹果",你不仅画了苹果,还画了果树、牛顿、地心引力...结果别人问你"苹果英语怎么说",你开始讲牛顿的故事。
在多项式回归中 :
如果次数选得太高(比如用10次多项式拟合5个数据点),曲线会完美穿过每个点,但变得极其扭曲,对新数据的预测反而变差。
为什么? 因为它记住了所有细节,包括随机误差,而不是学习真正的规律。
问题2:外推能力差------只能预测趋势内
生活类比:
你观察一个人1-20岁的身高增长,拟合得很好。但用这个模型预测他80岁的身高,可能得出"身高10米"的荒谬结论。
在多项式回归中 :
多项式曲线在数据范围外可能急剧上升或下降,与现实不符。咖啡温度预测中,它可能预测"100分钟后温度变成零下",但实际只会接近室温。
问题3:次数选择依赖经验
没有银弹:该用几次多项式?这需要尝试和验证,没有固定公式。
平衡的艺术:
四、使用范围:什么时候该用它?
✅ 适合用它的情况:
1. 有明显趋势的非线性数据
- 商品销量随时间变化(先增长后饱和)
- 药物剂量与疗效关系(太少无效,太多有毒)
- 学习时间与成绩关系(开始进步快,后来变慢)
2. 变量关系可解释
- 你知道x和y有关系,但不确定是不是直线关系
- 你想看到"随着x增加,y如何变化"的整体趋势
3. 数据量适中
- 通常样本数 > 10×多项式次数
❌ 不适合用它的情况:
1. 分类问题
- 比如判断邮件是否是垃圾邮件(结果是"是/否")
- 这类问题适合逻辑回归、决策树等
2. 超高维数据
- 比如图像识别(一张图有上万像素点)
- 这类问题适合卷积神经网络(CNN)
3. 复杂非线性关系
- 比如股票价格预测(受无数因素影响)
- 可能需要更复杂的模型,如神经网络
简单判断标准:
如果你的数据画在图上,眼睛能看出某种曲线趋势,多项式回归就值得一试。
五、应用场景:它在现实世界中的身影
案例1:电商销量预测 🛒
问题:新产品上架后,如何预测未来销量?
多项式回归的作用:
收集前30天销量 → 发现是"先快速增长,后趋于平稳"的曲线 →
用2次多项式拟合 → 预测下个月销量 → 指导库存管理为什么用多项式? 因为销量增长很少是直线,多项式能捕捉"增长放缓"的趋势。
案例2:医疗剂量反应研究 💊
问题:研发新药时,确定最佳剂量。
多项式回归的作用:
给不同组小白鼠不同剂量 → 记录疗效数据 →
发现"剂量太低无效,剂量适中最好,剂量太高有害" →
用2次或3次多项式找到"疗效最高点"对应的剂量为什么用多项式? 这种"先升后降"的关系,直线无法描述。
案例3:气候变化趋势分析 🌡️
问题:分析全球气温变化是线性上升还是加速上升?
多项式回归的作用:
分析过去100年气温数据 →
比较1次和2次多项式拟合效果 →
发现2次多项式拟合更好 → 得出"气温在加速上升"的结论为什么用多项式? 可以区分"匀速变化"和"加速变化",这对气候政策很重要。
案例4:设备寿命预测 🔧
问题:根据机器使用时间预测故障概率。
多项式回归的作用:
收集机器运行数据 →
发现"初期故障率低,中期稳定,后期急剧升高" →
用3次多项式描述这种"浴盆曲线" → 制定预防性维护计划案例5:教育心理学研究 📚
问题:每天学习多少小时效率最高?
多项式回归的作用:
调查学生学习时间与成绩关系 →
发现"1-2小时效果明显,3-4小时最佳,超过5小时反而下降" →
用2次多项式找到"效率最高点"六、Python实践案例:预测学习时间与成绩关系
让我们亲手实现一个简单的例子:
python
# 导入必要的库(工具包)
import numpy as np # 处理数据的工具
import matplotlib.pyplot as plt # 画图的工具
from sklearn.preprocessing import PolynomialFeatures # 多项式特征生成器
from sklearn.linear_model import LinearRegression # 回归模型
from sklearn.metrics import mean_squared_error # 评估误差的工具
# 1. 创建示例数据:学习时间 vs 考试成绩
# 假设我们调查了10个学生
study_hours = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]).reshape(-1, 1) # 学习时间(小时)
exam_scores = np.array([55, 65, 75, 82, 85, 88, 90, 91, 90, 89]) # 考试成绩(分)
# 2. 可视化原始数据
print("=== 数据可视化 ===")
plt.figure(figsize=(10, 6))
plt.scatter(study_hours, exam_scores, color='blue', s=100, label='真实数据')
plt.xlabel('学习时间(小时)', fontsize=12)
plt.ylabel('考试成绩(分)', fontsize=12)
plt.title('学习时间与考试成绩关系', fontsize=14)
plt.grid(True, alpha=0.3)
plt.legend()
plt.show()
# 3. 尝试不同的多项式次数
degrees = [1, 2, 3, 5] # 分别尝试1次、2次、3次、5次多项式
colors = ['red', 'green', 'purple', 'orange']
labels = ['线性(1次)', '2次多项式', '3次多项式', '5次多项式']
plt.figure(figsize=(12, 8))
plt.scatter(study_hours, exam_scores, color='blue', s=100, label='真实数据', zorder=5)
# 生成更密集的时间点用于画出平滑曲线
hours_plot = np.linspace(0, 11, 100).reshape(-1, 1)
for i, degree in enumerate(degrees):
print(f"\n=== 使用{degree}次多项式拟合 ===")
# 创建多项式特征
poly = PolynomialFeatures(degree=degree)
X_poly = poly.fit_transform(study_hours)
# 训练模型
model = LinearRegression()
model.fit(X_poly, exam_scores)
# 预测
X_plot_poly = poly.transform(hours_plot)
scores_pred = model.predict(X_plot_poly)
# 计算训练误差
train_pred = model.predict(X_poly)
mse = mean_squared_error(exam_scores, train_pred)
print(f"训练误差(均方误差): {mse:.2f}")
print(f"模型公式: y = {model.intercept_:.2f}", end="")
for j in range(1, degree+1):
print(f" + {model.coef_[j]:.2f}x^{j}", end="")
print()
# 画图
plt.plot(hours_plot, scores_pred, color=colors[i], linewidth=2.5,
label=labels[i], alpha=0.8)
plt.xlabel('学习时间(小时)', fontsize=12)
plt.ylabel('考试成绩(分)', fontsize=12)
plt.title('不同次数多项式拟合效果对比', fontsize=14)
plt.xlim([0, 11])
plt.ylim([50, 100])
plt.grid(True, alpha=0.3)
plt.legend()
plt.show()
# 4. 分析不同模型的预测效果
print("\n=== 模型效果分析 ===")
print("1次多项式(线性): 假设成绩随学习时间直线增长")
print("2次多项式: 能捕捉'收益递减'现象,学习效果先快后慢")
print("3次多项式: 拟合更好,但可能开始过拟合")
print("5次多项式: 明显过拟合,曲线为了穿过每个点而扭曲")
# 5. 用最佳模型(2次)进行预测
print("\n=== 使用2次多项式进行预测 ===")
best_degree = 2
poly_best = PolynomialFeatures(degree=best_degree)
X_poly_best = poly_best.fit_transform(study_hours)
model_best = LinearRegression()
model_best.fit(X_poly_best, exam_scores)
# 预测一些新情况
new_hours = np.array([2.5, 7.5, 11, 15]).reshape(-1, 1) # 包括数据范围内外
new_hours_poly = poly_best.transform(new_hours)
predictions = model_best.predict(new_hours_poly)
for hours, score in zip(new_hours.flatten(), predictions):
print(f"学习{hours}小时,预测成绩: {score:.1f}分")
# 6. 重要提醒
print("\n" + "="*50)
print("⚠️ 重要发现与提醒:")
print("="*50)
print("1. 2次多项式最合理:它显示了'学习收益递减'规律")
print("2. 5次多项式过拟合:完美拟合训练数据,但预测异常值会出错")
print("3. 注意外推风险:预测15小时学习得85.7分可能不靠谱")
print("4. 真实应用时:需要更多数据,并用部分数据验证模型")运行这个代码,你会看到:
- 原始数据点显示"先快后慢"的增长趋势
- 不同次数多项式的拟合曲线
- 1次多项式(直线)明显不合适
- 2次多项式(抛物线)很好地捕捉了趋势
- 5次多项式过度弯曲,虽然穿过所有点,但预测11小时后的成绩反而不合理