Antrl4 入门 —— 使用Antrl4实现一个表达式计算器

一、引言

在编译原理中，"解析"是将文本转化为计算机可理解结构的核心步骤，主要分为两步：词法分析和语法分析。我们用最常见的四则运算"(12+3)4-5"，就能直观理解这个过程。

1. 词法分析： 就像我们读句子先拆出词语，词法分析会把输入文本拆成一个个"词法单元"（token），剔除空格、换行等无关内容。我们将例子替换为更贴近实际的带括号表达式"(12+3)4-5"，最终会拆出 9 个 Token：左括号( 、数字1 2 、加号+ 、数字 3 、右括号) 、乘号 、数字 4 、减号- 、数字5，同时标记每个 Token 的类型（括号/数字/运算符）。

2. 语法分析： 基于词法分析得到的 Token 序列，按照语言规则（四则运算优先级、括号优先级最高）构建结构化的"抽象语法树（AST）"。对"(12+3)*4-5"，语法分析会先识别出括号内的"12+3"是一个子表达式，再将其结果与"4"进行乘法运算，最后减去"5"，明确运算顺序为"((12+3)*4)-5"。对应的抽象语法树如下：

graph TD A[减号] --> B[乘号] A --> C[5] B --> D[加号] B --> E[4] D --> F[左括号] D --> G[12] D --> H[3] D --> I[右括号]

如果我们手动实现词法分析器和语法分析器，细节较多，复杂度较高，而ANTLR4则可以帮我们解决这个问题 ------ 它专门负责自动完成"词法分析"和"语法分析"环节。

简单说，你只需用ANTLR4定义好目标语言的语法规则（比如四则运算的数字、运算符、优先级规则），它就能自动生成对应的词法分析器和语法分析器，还能直接输出AST，无需手动编写解析逻辑。并提供listener和vistor两种模式，遍历语法树，帮助你完成剩余流程。凭借强大的解析能力，ANTLR4 被广泛应用于各类开源框架中，比如：Spark SQL（解析 SQL 语句）、Hive（处理 HiveQL），是构建语言解析相关工具的主流选择。

二、定义词法&语法规则规则

在使用ANTLR4帮助我们解析表达式，需要先告诉ANTLR4表达式的规则，这个规则定义在ANTLR4中是一个语法文件，以.g4结尾。这个文件中，主要包含词法规则和语法规则，g4文件结构是这样的：

ini 复制代码

// 语法名称（需与文件名一致）
grammar 语法名称;

// 1. 词法规则（大写字母开头）
词法规则1 : 匹配模式;
词法规则2 : 匹配模式;

// 2. 语法规则（小写字母开头）
语法规则1 : 规则组合逻辑;
语法规则2 : 规则组合逻辑;

注意: 语法名称必须与 .g4 文件名完全一致（如语法名为 Calc，则文件名为 Calc.g4）；词法规则与语法规则通过首字母大小写严格区分，不可混淆。

PS: 也可以把词法分析和语法分析的文件分开，如果定义较为复杂的表达式规则（比如SQL解析），可以分开管理：

词法文件：文件名格式为 XXXLexer.g4，开头需用 lexer grammar XXXLexer; 声明（区别于组合语法的 grammar XXX;），仅包含词法规则（大写开头）；
语法文件：文件名格式为 XXXParser.g4，开头需用 parser grammar XXXParser; 声明，通过 import XXXLexer; 导入对应的词法文件，仅包含语法规则（小写开头）；
命名关联：词法文件与语法文件的前缀需一致（如 CalcLexer.g4 对应 CalcParser.g4），确保导入时能正确关联。

PS: ANTLR的全称是ANother Tool for Language Recognition（另一种语言识别工具）。

2.1 词法规则

词法规则的核心作用是定义"什么是合法的 Token"，对应我们上一章提到的"词法分析"环节。对于四则运算，需要识别的 Token 包括：左括号 (、右括号 )、运算符（+、-、*、/）、数字（整数，如 12、3）。它的基本组成为：

ini 复制代码

规则名 : 匹配模式 [-> 动作]; // 中括号表示动作可选

规则名： 首字母必须大写，推荐采用"全大写+下划线分隔"的语义化命名，比如INT，禁止使用 ANTLR4 关键字（如 grammar、mode）；
匹配模式: 匹配模式采用正则表达式的核心子集语法（并非完整标准正则），用于描述 Token 的文本格式，足以覆盖绝大多数词法分析场景，但需注意：标准正则中的部分复杂特性（如 \d、\w、反向引用、零宽断言等）不被支持。
可选动作配置: 动作通过 -> 引导，用于对匹配到的Token执行特定操作，入门常用的只有是 skip（跳过无关内容）。比如[ \t\r\n]+ -> skip;，即忽略空格、换行、制表符。其他在入门中不做介绍。
优先级规则：规则定义顺序即匹配优先级------先定义的规则优先级更高，优先匹配（如关键字需优先于标识符定义，否则会被误识别）。

以四则运算+简单函数为例：

antlr4 复制代码

// 1. 函数名规则：关键字优先，匹配max/min（不区分大小写可改为 [Mm][Aa][Xx]，此处统一大写）
MAX : 'MAX';  // 匹配MAX函数名
MIN : 'MIN';  // 匹配MIN函数名

// 2. 括号与分隔符规则
LEFT_PAREN  : '(';  // 匹配左括号 (
RIGHT_PAREN : ')';  // 匹配右括号 )
COMMA       : ',';  // 匹配参数分隔符 ,

// 3. 运算符规则：单个字符，直接匹配
ADD : '+';  // 加号
SUB : '-';  // 减号
MUL : '*';  // 乘号
DIV : '/';  // 除号

// 4. 整数规则：使用 [0-9]+ 匹配1位及以上数字
INT : [0-9]+;  // 可匹配 1、12、345 等整数，贪婪匹配特性保证完整匹配

// 5. 跳过无关内容：空格、制表符（\t）、回车（\r）、换行（\n）
WS  : [ \t\r\n]+ -> skip;  // 多个空白字符连续出现时，一次性跳过

PS: 如果所有规则，都不区分大小写，可以配置一个全局规则

antlr4 复制代码

options {
    caseInsensitive = true;
}

2.2 语法规则

语法规则的核心作用是定义"Token 如何组合才合法"，语法规则基础格式为：

ini 复制代码

规则名 : 规则体分支1 | 规则体分支2 ... [# 可选标签];

规则名： 小写字母开头（如 expr、term），建议使用"全小写+下划线"的方式命名；
规则体： 词法名字组合 + 正则的分组（也就是括号）& 匹配次数（如 *、?）,多个分支用 | 分隔；
可选标签： 用 # 开头，用于区分同一规则的不同分支（便于后续遍历 AST ），
规则优先级： 可以有多个规则，互相引用，被引用的优先级更高。

好，接下来我们开始定义四则运算的加减法：

sql 复制代码

expr : INT (ADD | SUB) INT

等等，这里有个问题，这只能识别两个整数的加减法，那三个呢、四个呢？！好像可以这样定义：

sql 复制代码

expr : INT ((ADD | SUB) INT)*

还是哪里不对，如果加法左右不止是整数呢，比如 MAX(1,2)+3，再比如1+2*3。这里必须引入递归，也就是说，需要自己定义自己。

比如这样：

bash 复制代码

expr : INT
     | expr (ADD | SUB) expr

那怎么定义优先级呢，比如括号优先级最高比乘除法高，乘除法比加减法高 ------ 同一个语法规则下，书写顺序就是优先级，也就是前面的优先级高。

那么带有函数的完整的语法定义就是：

bash 复制代码

expr : (MAX | MIN) LEFT_PAREN expr (COMMA expr)* LEFT_PAREN # FuncCallExpr
     | INT # IntExpr 
     | LEFT_PAREN expr RIGHT_PAREN # ParenExpr
     | expr (MUL | DIV) expr # MulDivExpr
     | expr (ADD | SUB) expr # AddSubExpr
     ;

2.3 完整配置文件

把词法和语法文件合并到一起，就得到了完整的配置文件：

css 复制代码

grammar Calc;

// 词法规则（新增函数名、逗号）
MAX         : 'MAX';  // MAX函数名
MIN         : 'MIN';  // MIN函数名
LEFT_PAREN  : '(';
RIGHT_PAREN : ')';
COMMA       : ',';  // 参数分隔符
ADD         : '+';
SUB         : '-';
MUL         : '*';
DIV         : '/';
INT         : [0-9]+;
WS          : [ \t\r\n]+ -> skip;

expr : (MAX | MIN) LEFT_PAREN expr (COMMA expr)* RIGHT_PAREN # FuncCallExpr
     | INT # IntExpr 
     | LEFT_PAREN expr RIGHT_PAREN # ParenExpr
     | expr (MUL | DIV) expr # MulDivExpr
     | expr (ADD | SUB) expr # AddSubExpr
     ;

三、测试 & 生成代码

3.1 测试

有了配置文件，我们可以通过idea的插件验证。在idea的插件市场，搜索antrl4，安装即可。安装完成后，选中语法，右键Test Rule。输入表达式，就可以看到，转为了抽象语法树：

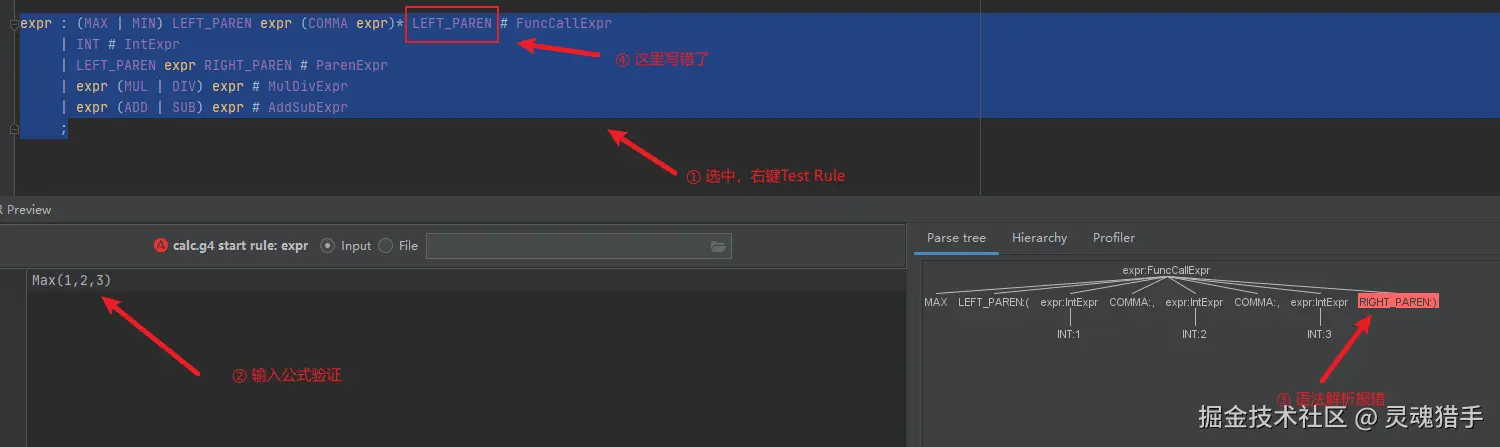
3.2 代码生成

测试没有问题后，我们就可以生成代码了。

配置代码生成的位置： 选择g4文件，右键Configuration ANTLR。
- "Output directory where all output is generated" --> java目录
- "Package/namespace for the generated code" --> 包名
代码生成： 点击g4文件，右键Generate ANTLR Recognition生成即可。

这样代码就愉快的生成了：

{GrammarName}Lexer.java --> 词法解析器；
{GrammarName}Parser.java --> 语法解析器；
监听器：提供被动监听的方式遍历语法树方法，当遍历器进入（enter）或退出（exit）树的某个节点时，自动调用监听器中对应的方法（如 enterIntExpr、exitIntExpr）。
- 接口：{GrammarName}Listener.java
- 默认实现：{GrammarName}BaseListener.java
访问者：提供主动遍历语法树的方法，我们需要显式调用 visit(child) 方法访问子节点，并可以返回结果。
- 接口：{GrammarName}Visitor.java
- 默认实现：{GrammarName}BaseVisitor.java
其他文件：还有些.tokens 文件（记录词汇符号的映射关系）和 .interp 文件（用于调试），通常可以忽略。

3.3 如何使用

接下来，我们梳理下这些生成的代码该如何使用，这里有个基本范式：

java 复制代码

// 构造字符流
CharStream input = CharStreams.fromString("1+2*3");
// 词法解析
CalcLexer lexer = new CalcLexer(input);
CommonTokenStream tokens = new CommonTokenStream(lexer);
// 语法解析，生成语法树
CalcParser parser = new CalcParser(tokens);
ParseTree tree = parser.expr();

// 使用listener、visitor遍历语法树
// todo ...

3.3.1 listener模式

先看下生成的listener的继承关系

ParseTreeListener：ANTLR4 中用于监听语法树遍历事件的核心接口，定义了最基础的事件回调。注意，这个不是自动生成的。
- CalcListener：根据你的语法，生成的接口，在我们这个例子中，会自动生成类似enter/exitInt、enter/exitMaxFunc这样的方法。
  - CalcBaseListener：CalcListener的基础实现类，典型的适配器模式，实现了CalcListener接口所有方法，但什么都没做。这样你写一个继承CalcBaseListener的方法时，就可以按需实现，而不是实现所有接口。

ParseTreeListener接口方法。

java 复制代码

public interface ParseTreeListener { 
    // 进入任意规则节点时触发 
    void enterEveryRule(ParserRuleContext ctx); 
    // 退出任意规则节点时触发 
    void exitEveryRule(ParserRuleContext ctx); 
    // 访问终端节点（叶子节点）时触发 
    void visitTerminal(TerminalNode node); 
    // 访问错误节点（语法错误节点）时触发 
    void visitErrorNode(ErrorNode node); 
}

而CalcListener接口则是enter/exit我们自定义的语法规则的方法：

java 复制代码

/**
 * Enter a parse tree produced by the {@code MulDivExpr}
 * labeled alternative in {@link calcParser#expr}.
 * @param ctx the parse tree
 */
void enterMulDivExpr(calcParser.MulDivExprContext ctx);
/**
 * Exit a parse tree produced by the {@code MulDivExpr}
 * labeled alternative in {@link calcParser#expr}.
 * @param ctx the parse tree
 */
void exitMulDivExpr(calcParser.MulDivExprContext ctx);

// 省略了一些其他方法。。。

这里咱们简单的在Listener中打印一下，看下遍历顺序：

java 复制代码

public class TraversalListener extends calcBaseListener {
    private int indent = 0; // 用于缩进显示层级

    @Override
    public void enterEveryRule(ParserRuleContext ctx) {
        printWithIndent("进入节点: " + ctx.getClass().getSimpleName());
        indent++;
    }

    @Override
    public void exitEveryRule(ParserRuleContext ctx) {
        indent--;
        printWithIndent("退出节点: " + ctx.getClass().getSimpleName());
    }

    @Override
    public void visitTerminal(TerminalNode node) {
        printWithIndent("访问叶子节点: " + node.getText());
    }

    private void printWithIndent(String message) {
        System.out.println(StringUtils.repeat("->", indent) + message);
    }

    public static void main(String[] args) {
        String expr = "1+2*3-5";
        System.out.println("表达式: " + expr + "\n遍历顺序:");

        // 解析为抽象语法树
        CharStream input = CharStreams.fromString(expr);
        calcLexer lexer = new calcLexer(input);
        CommonTokenStream tokens = new CommonTokenStream(lexer);
        calcParser parser = new calcParser(tokens);
        ParseTree tree = parser.expr();
        // 遍历监听
        ParseTreeWalker.DEFAULT.walk(new TraversalListener(), tree);
    }
}

输出

rust 复制代码

进入节点: AddSubExprContext
->进入节点: AddSubExprContext
->->进入节点: IntExprContext
->->->访问叶子节点: 1
->->退出节点: IntExprContext
->->访问叶子节点: +
->->进入节点: MulDivExprContext
->->->进入节点: IntExprContext
->->->->访问叶子节点: 2
->->->退出节点: IntExprContext
->->->访问叶子节点: *
->->->进入节点: IntExprContext
->->->->访问叶子节点: 3
->->->退出节点: IntExprContext
->->退出节点: MulDivExprContext
->退出节点: AddSubExprContext
->访问叶子节点: -
->进入节点: IntExprContext
->->访问叶子节点: 5
->退出节点: IntExprContext
退出节点: AddSubExprContext

对比抽象语法树，不难看出，按照进入节点的顺序，是根->左->右的方式，深度优先遍历；按照出节点的顺序，则是左->右->根的顺序。

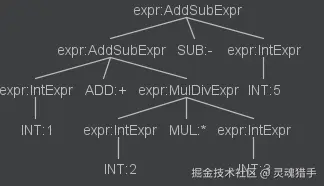
3.3.2 visitor模式

先看下visitor模式的继承关系：

ParseTreeVisitor<T>: 基础接口，类似ParseTreeListener定义了比如visit、visitChildren这种基础方法。
- CalcVisitor<T>:自动生成的接口，包含visitXXX这样我们自定义的语法的接口方法。
- AbstractParseTreeVisitor<T>抽象类，ParseTreeVisitor的最基本实现。
  - CalcBaseVisitor<T>: 自动生成的继承自AbstractParseTreeVisitor<T>,实现了CalcVisitor<T>的抽象类，也是典型的适配器，内部的所有实现都是return visitChildren(ctx);。也就是继续向下遍历。

介绍下最基础的ParseTreeVisitor<T>

泛型T，是每个访问方法，需要返回的类型。
visit(ParseTree tree)：启动对整个语法树的遍历；
visitChildren(RuleNode node)：遍历节点的子节点并返回汇总结果；
visitTerminal(TerminalNode node)：访问终端节点（叶子节点）；
visitErrorNode(ErrorNode node)：访问错误节点。

他的基础实现类AbstractParseTreeVisitor<T>，典型的模板模式，主要实现了基础的visit和visitChildren方法：

java 复制代码

public T visit(ParseTree tree) {
    //启动遍历
    return tree.accept(this);
}

public T visitChildren(RuleNode node) {
    //遍历所有的子节点
    T result = this.defaultResult();//默认返回null，供子类复写。
    int n = node.getChildCount();

    for(int i = 0; i < n && this.shouldVisitNextChild(node, result); ++i) {
        ParseTree c = node.getChild(i);
        T childResult = c.accept(this);
        result = this.aggregateResult(result, childResult);//如何合并两个子节点的值，默认返回后面的
    }

    return result;
}

protected T defaultResult() {
    return null;
}

protected T aggregateResult(T aggregate, T nextResult) {
    return nextResult;
}

上文也说过了，自动生成的CalcBaseVisitor<T>实现的所有方法，内部的所有实现都是return visitChildren(ctx);，也就是上面AbstractParseTreeVisitor<T>的方法。

咱们也简单实现一个visitor，就输入是什么，原样输出出来：

java 复制代码

@Override
public String visitTerminal(TerminalNode node) {
    return node.getText();
}

@Override
protected String aggregateResult(String aggregate, String nextResult) {
    if(aggregate == null) return nextResult;
    if(nextResult == null) return aggregate;
    return aggregate + nextResult;
}

public static void main(String[] args) {
    CharStream input = CharStreams.fromString("1+2+3+4");
    CalcLexer lexer = new CalcLexer(input);
    CommonTokenStream tokens = new CommonTokenStream(lexer);
    CalcParser parser = new CalcParser(tokens);
    String visit = new TraversalVisitor().visit(parser.expr());
    System.out.println(visit);
}

这里重写了AbstractParseTreeVisitor<T>的

visitTerminal:叶子节点返回节点的文本。
aggregateResult:合并两个节点的值，把字符串拼接起来。

输出

复制代码

1+2+3+4

我们简单的实现加法：

java 复制代码

@Override
public String visitAddSubExpr(CalcParser.AddSubExprContext ctx) {

    if(ctx.ADD() != null){
        //递归获取左右两侧的值
        String left = visit(ctx.expr(0));
        String right = visit(ctx.expr(1));
        if(NumberUtils.isDigits(left) && NumberUtils.isDigits(right)){
            int result = Integer.parseInt(right) + Integer.parseInt(left);
            return Integer.toString(result);
        }
    }

    return super.visitAddSubExpr(ctx);
}

那么上面的1+2+3+4就会输出10。当然，一旦有其他运算，这里就不灵了，不过起码我们离计算器近了一步，下一章我们具体实现。

四、实战

4.1 需求

接下来我们开始实战，就搞一个极简的表达式计算器吧，需要实现以下功能：

支持变量，变量名：首字符为字母或者下划线，后续字符可为字母、数字或者下划线，大小写敏感；
支持整数和小数；
支持四则运算以及括号；
支持函数，本次仅实现MAX/MIN，大小写不敏感。

4.2 语法文件

ini 复制代码

grammar Calc;

// 词法规则
MAX         : [Mm][Aa][Xx];  // MAX函数名
MIN         : [Mm][Ii][Nn];  // MIN函数名
LEFT_PAREN  : '(';
RIGHT_PAREN : ')';
COMMA       : ',';
ADD         : '+';
SUB         : '-';
MUL         : '*';
DIV         : '/';
VAR         : [a-zA-Z_][a-zA-Z0-9_]*;
INT         : [0-9]+;
FLOAT       : [0-9]+; // 带符号小数
WS          : [ \t\r\n]+ -> skip;
// 语法规则
number : INT | FLOAT;
function : MAX LEFT_PAREN expr (COMMA expr)* RIGHT_PAREN # maxFunc
         | MIN LEFT_PAREN expr (COMMA expr)* RIGHT_PAREN # minFunc
         ;
expr : function # FuncCallExpr
     | number # numberExpr
     | VAR # varExpr
     | LEFT_PAREN expr RIGHT_PAREN # ParenExpr
     | expr (MUL | DIV) expr # MulDivExpr
     | expr (ADD | SUB) expr # AddSubExpr
     | (ADD | SUB) expr # UnaryMinusPlus
     ;

与之前的语法文件区别不大

新增了变量词法，VAR: [a-zA-Z_][a-zA-Z0-9_]*，注意要放在函数名的后面，否则函数名字会被解析成变量名字。
新增小数，并在后面与整数一起合并为number。
function单拿出来作为一个语法，被expr引用，这种写法与之前区别不大，只是生成的代码中，会多一个visitFuncCallExpr(visitor模式)或者enter/exitFuncCallExpr(listener模式)的方法。
增加了 (ADD | SUB) expr这样的语法，以支持正负数这样的写法。

Q ：为什么不再INT/FLOAT上直接支持正负号呢？ A : 这接定义会和加减法冲突，目前我没想好解决方案，所以在后面加了一个 (ADD | SUB) expr表达式。

4.3 使用Visitor实现

上一章节，我们使用visitor实现了，仅能支持加法的计算器，这里我们把所有的语法都实现一遍，也就实现了计算器，注意这里的泛型改为Double了。

java 复制代码

public class CalcVisitorEvaluator extends CalcBaseVisitor<Double> {

    private final Map<String, Double> variables;

    public CalcVisitorEvaluator(Map<String, Double> variables) {
        this.variables = variables;
    }

    @Override
    public Double visitNumberExpr(CalcParser.NumberExprContext ctx) {
        return Double.parseDouble(ctx.number().getText());
    }

    @Override
    public Double visitVarExpr(CalcParser.VarExprContext ctx) {
        return variables.getOrDefault(ctx.VAR().getText(), 0.0);
    }

    @Override
    public Double visitParenExpr(CalcParser.ParenExprContext ctx) {
        return visit(ctx.expr());
    }

    @Override
    public Double visitMulDivExpr(CalcParser.MulDivExprContext ctx) {
        double left = visit(ctx.expr(0));
        double right = visit(ctx.expr(1));
        if (ctx.MUL() != null) {
            return left * right;
        } else {
            return left / right;
        }
    }

    @Override
    public Double visitAddSubExpr(CalcParser.AddSubExprContext ctx) {
        double left = visit(ctx.expr(0));
        double right = visit(ctx.expr(1));
        if (ctx.ADD() != null) {
            return left + right;
        } else {
            return left - right;
        }
    }

    @Override
    public Double visitUnaryMinusPlus(CalcParser.UnaryMinusPlusContext ctx) {
        double value = visit(ctx.expr());
        return ctx.SUB() != null ? -value : value;
    }

    @Override
    public Double visitMaxFunc(CalcParser.MaxFuncContext ctx) {
        double max = Double.NEGATIVE_INFINITY;
        for (CalcParser.ExprContext expr : ctx.expr()) {
            max = Math.max(max, visit(expr));
        }
        return max;
    }

    @Override
    public Double visitMinFunc(CalcParser.MinFuncContext ctx) {
        double min = Double.POSITIVE_INFINITY;
        for (CalcParser.ExprContext expr : ctx.expr()) {
            min = Math.min(min, visit(expr));
        }
        return min;
    }

    @Override
    public Double visitFuncCallExpr(CalcParser.FuncCallExprContext ctx) {
        return visit(ctx.function());
    }
}

是不是看起来很简单，只不过是把所有的简单的语法都实现了一遍，复杂的词法语法分析，以及语法树的遍历，都不需要自行实现了。

下面我们验证一下：

java 复制代码

public static void main(String[] args) {
    Map<String, Double> variables = new HashMap<>();
    variables.put("a", 10.0);
    variables.put("b", 6.0);
    String expression = "max(a + 5, min(b * 3, 20)) - 3";

    // 使用Visitor模式计算
    CalcParser.ExprContext exprContext = parseTree(expression);
    CalcVisitorEvaluator visitor = new CalcVisitorEvaluator(variables);
    double visitorResult = visitor.visit(exprContext);
    System.out.println("Visitor结果: " + visitorResult);
}

public static CalcParser.ExprContext parseTree(String expression) {
    CharStream input = CharStreams.fromString(expression);
    CalcLexer lexer = new CalcLexer(input);
    CommonTokenStream tokens = new CommonTokenStream(lexer);
    CalcParser parser = new CalcParser(tokens);
    return parser.expr();
}

输出

makefile 复制代码

Visitor结果: 15.0

是不是很神奇，我们简单梳理下遍历操作，语法树如下，根节点是这个减法。回头看下代码，减法就是先遍历计算左子节点的值，再遍历计算右子节点，把他们减起来就可以了。其实就是一个左右根的递归遍历，沿着这个顺序，就会一直递归到左下的加法分支。

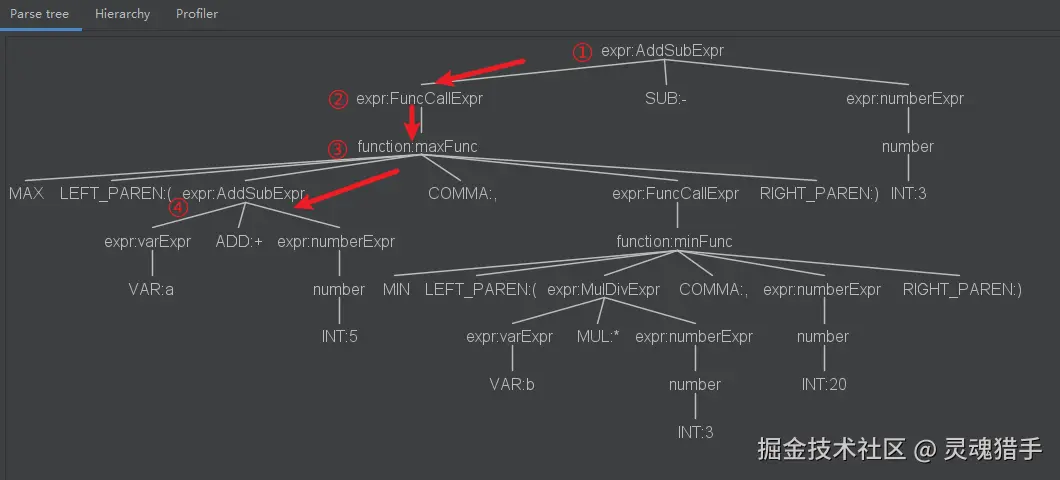
左下的加法计算完成后，就变成了这样。再遍历max的右边的节点，又到了中间的乘法，再进行乘法计算：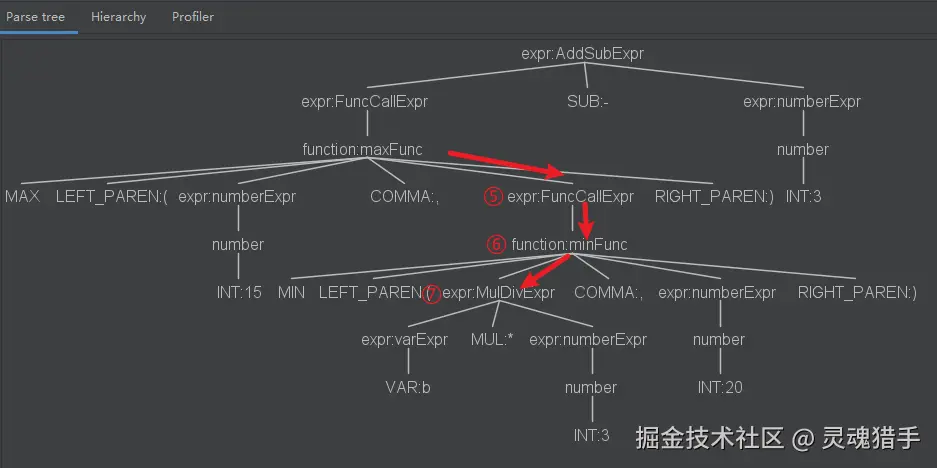

嗯，我相信你已经看懂是如何计算的了，我就不继续截图了。总之随着语法树的自底向上遍历，不断计算，汇总到根节点，就得到结果了。

4.4 使用Listener实现

在visitor模式下，我们对语法树使用左右根的方式遍历整棵语法树，自底向上，把结果计算出来。在listener模式，也类似，不过listener没有返回值，在进入节点时，需要利用栈这种数据结构，把数据先存储起来，出栈再去计算：

java 复制代码

public class CalcListenerEvaluator extends CalcBaseListener {
    private final Map<String, Double> variables;
    private final Deque<Double> stack = new ArrayDeque<>();

    public CalcListenerEvaluator(Map<String, Double> variables) {
        this.variables = variables;
    }

    public Double getResult() {
        return stack.isEmpty() ? 0.0 : stack.pop();
    }

    @Override
    public void exitNumberExpr(CalcParser.NumberExprContext ctx) {
        String text = ctx.number().getText();
        stack.push(Double.parseDouble(text));
    }

    @Override
    public void exitVarExpr(CalcParser.VarExprContext ctx) {
        String varName = ctx.VAR().getText();
        Double value = variables.getOrDefault(varName, 0.0);
        stack.push(value);
    }

    @Override
    public void exitParenExpr(CalcParser.ParenExprContext ctx) {
        // 括号表达式结果已在子表达式处理后入栈，无需额外操作
    }

    @Override
    public void exitMulDivExpr(CalcParser.MulDivExprContext ctx) {
        double right = stack.pop();
        double left = stack.pop();
        if (ctx.MUL() != null) {
            stack.push(left * right);
        } else {
            stack.push(left / right);
        }
    }

    @Override
    public void exitAddSubExpr(CalcParser.AddSubExprContext ctx) {
        double right = stack.pop();
        double left = stack.pop();
        if (ctx.ADD() != null) {
            stack.push(left + right);
        } else {
            stack.push(left - right);
        }
    }

    @Override
    public void exitUnaryMinusPlus(CalcParser.UnaryMinusPlusContext ctx) {
        double value = stack.pop();
        if (ctx.SUB() != null) {
            stack.push(-value);
        }
        // 一元加号不改变值
    }

    @Override
    public void exitMaxFunc(CalcParser.MaxFuncContext ctx) {
        List<CalcParser.ExprContext> exprs = ctx.expr();
        double max = stack.pop();
        for (int i = 1; i < exprs.size(); i++) {
            max = Math.max(max, stack.pop());
        }
        stack.push(max);
    }

    @Override
    public void exitMinFunc(CalcParser.MinFuncContext ctx) {
        List<CalcParser.ExprContext> exprs = ctx.expr();
        double min = stack.pop();
        for (int i = 1; i < exprs.size(); i++) {
            min = Math.min(min, stack.pop());
        }
        stack.push(min);
    }

}

下面我们验证一下：

java 复制代码

public static void main(String[] args) {
    Map<String, Double> variables = new HashMap<>();
    variables.put("a", 10.0);
    variables.put("b", 6.0);
    String expression = "max(a + 5, min(b * 3, 20)) - 3";

    // 使用Listener模式计算
    CalcListenerEvaluator listener = new CalcListenerEvaluator(variables);
    ParseTreeWalker.DEFAULT.walk(listener, exprContext);
    System.out.println("Listener结果: " + listener.getResult());
}

输出

makefile 复制代码

Visitor结果: 15.0

listener模式，我们也简单捋一下。还是这张图，从根节点开始遍历，一直向下：

直到遇到左侧加法的变量节点，入栈a,也就是10，再遍历加法右侧的数字节点，入栈5，这时栈的样子为：

rust 复制代码

栈底 -> 10 -> 5 -> 栈顶

然后回到AddSubExpr节点，执行exitAddSubExpr方法：

scss 复制代码

@Override
public void exitAddSubExpr(CalcParser.AddSubExprContext ctx) {
    double right = stack.pop();
    double left = stack.pop();
    if (ctx.ADD() != null) {
        stack.push(left + right);
    } else {
        stack.push(left - right);
    }
}

计算了10+5，并把结果15入栈：

rust 复制代码

栈底 -> 15 -> 栈顶

继续遍历，到中间的乘法节点，继续入栈b和3，那么现在是：

rust 复制代码

栈底 -> 15 -> 6-> 3 -> 栈顶

乘法也是从栈里取出两个数，计算再放回去，那么栈现在是：

rust 复制代码

栈底 -> 15 -> 18 -> 栈顶

是不是有点感觉了，伴随这样不断入栈出栈，栈中最终的结果，就是出根节点后计算的结果，也就是最终结果。

五、总结

只需要定义语法规则，ANTRL4帮我们实现了比较复杂的词法、语法解析，并提供visitor和listener两种模式，协助遍历抽象语法树，让复杂的语法解析，瞬间变得简单。ANTRL4在很多开源软件中，都有应用，比如SPARK、HIVE的语法解析。

另外

咱们实现的表达是计算，仅仅是能用，每次计算都需要重新解析，性能较差。一个可行的思路是，解析后直接生成java字节码，并缓存以提升性能。表达式引擎aviator就是这么做的，不过，aviator并没有使用ANTRL4。如果你需要这样一个表达式解析器，推荐aviator，没必要重复造轮子。
文章里总写根左右或者左右根这种遍历方式，实际上这是二叉树的概念，应用的并不准确。
语法文件编写是很复杂的，这里讲的很简略，可以在B站上看下这个# 【antlr】Antlr4从入门到精通
源码上传了Gitee，可以自取。