C++ STL 栈与队列完全指南：从容器使用到算法实现

目录

• 前言
• 一、栈和队列的使用
• 二、栈和队列相关算法题
• • [2.1 最小栈](#2.1 最小栈)
  • [2.2 栈的压入、弹出序列](#2.2 栈的压入、弹出序列)
  • [2.3 逆波兰表达式求值](#2.3 逆波兰表达式求值)
  • [2.4 二叉树的层序遍历（广度优先搜索（BFS））](#2.4 二叉树的层序遍历（广度优先搜索（BFS））)
• 结语

🎬 云泽Q ：个人主页
🔥 专栏传送入口 : 《C语言》《数据结构》《C++》《Linux》《蓝桥杯系列》

⛺️遇见安然遇见你，不负代码不负卿~

---

前言

大家好啊，我是云泽Q，欢迎阅读我的文章，一名热爱计算机技术的在校大学生，喜欢在课余时间做一些计算机技术的总结性文章，希望我的文章能为你解答困惑~

一、栈和队列的使用

由于栈要保持其结构特点（进出数据是后进先出），栈是不支持迭代器的

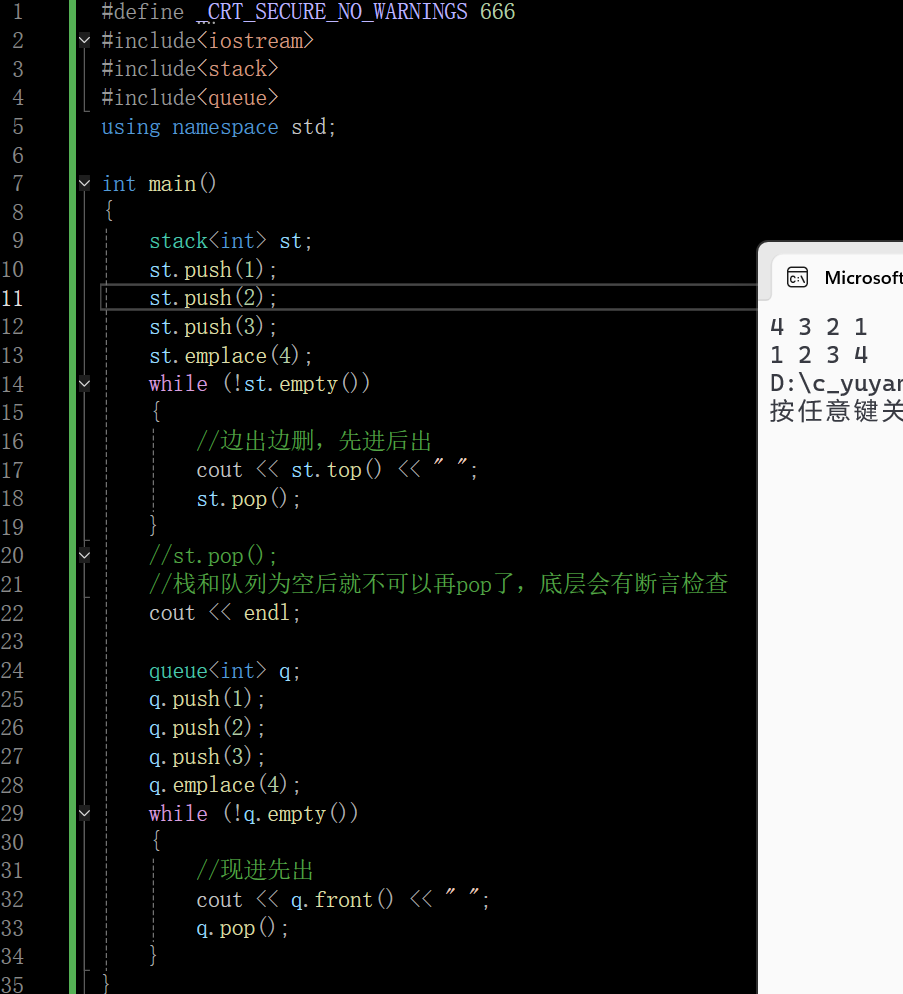
队列的头文件下有两个队列，一个叫普通队列，一个叫优先级队列，优先级队列更复杂一些，其底层的结构就是堆

二、栈和队列相关算法题

2.1 最小栈

最小栈

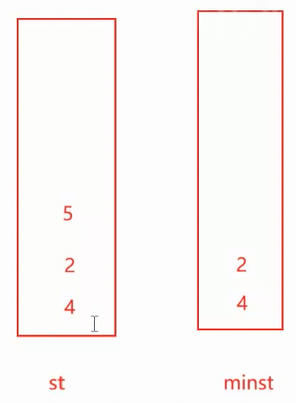
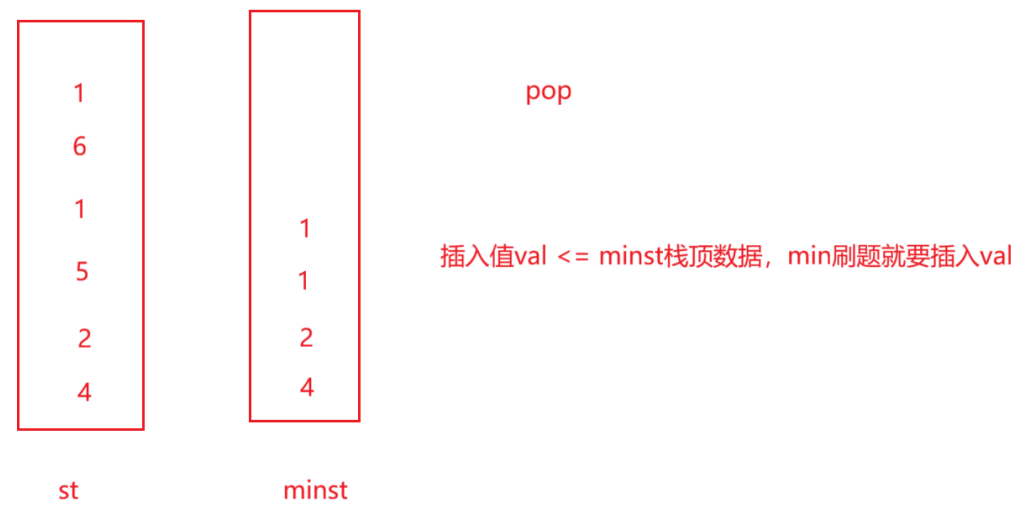
这里的解决方法是用两个栈，第一个栈st是正常的栈，第二个栈minst用来记录最小数据，左边的栈进一个4，右边栈也进一个4，只要插入的数据比前一个数据小，minst这个栈就进数据，或者minst为空，也进数据，以此类推

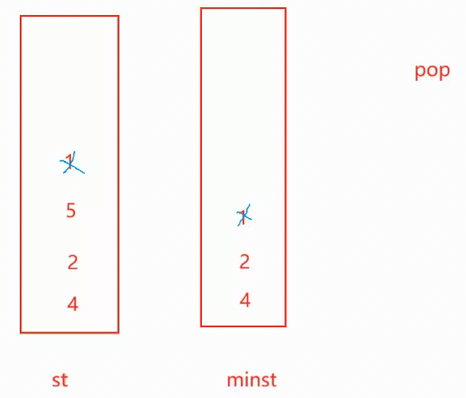
此时当所有数据插入完成后，再进行pop，getMin就可以获得2了

还有一个点，若左边插入和右边一样大小的值，右边的栈也要插入

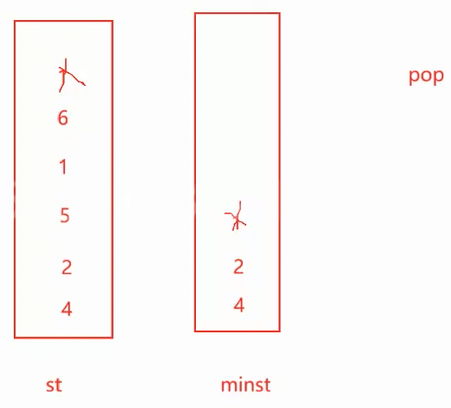
例如现在插入和1一样大小的值，右边不插入的话，此时若pop（左边删除的值若和右边的值相等，则右边也要删除，要更新下一个最小值，但是下一个左边删除6，右边的值是不删除的），右边的1被删除后，更新的下一个最小值变为2了，但实际上最小值为1

class MinStack {
public:
    MinStack() {
        
    }
    
    void push(int val) {
        if(_minst.empty() || val <= _minst.top())
            _minst.push(val);
        _st.push(val);
    }
    
    void pop() {
        if(_minst.top() == _st.top())
            _minst.pop();
        _st.pop();
    }
    
    int top() {
        return _st.top();
    }
    
    int getMin() {
        return _minst.top();
    }
private:
    stack<int> _st;
    stack<int> _minst;
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(val);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->getMin();
 */

说一下这里代码的构造过程

MinStack的私有成员是两个stack< int >类型的对象：

• _st：主栈，用于存储所有元素；
• _minst：辅助栈，用于存储当前栈中的最小值。
  当创建一个MinStack对象时（比如MinStack ms;），构造过程会按以下步骤执行：

步骤 1：自动初始化成员对象（_st和_minst）

在执行MinStack的构造函数体之前，C++ 会先自动调用成员对象自身的默认构造函数：

• _st会调用stack< int >的默认构造函数，初始化一个空的主栈；
• _minst会调用stack< int >的默认构造函数，初始化一个空的辅助栈。

（注：stack是 STL 容器，它的默认构造函数本身就是创建一个空栈）

步骤 2：执行MinStack的构造函数体

显式定义的MinStack()构造函数体是空的（{}），所以这一步没有额外操作。

当然把MinStack()构造函数删了也可以

2.2 栈的压入、弹出序列

栈的压入、弹出序列

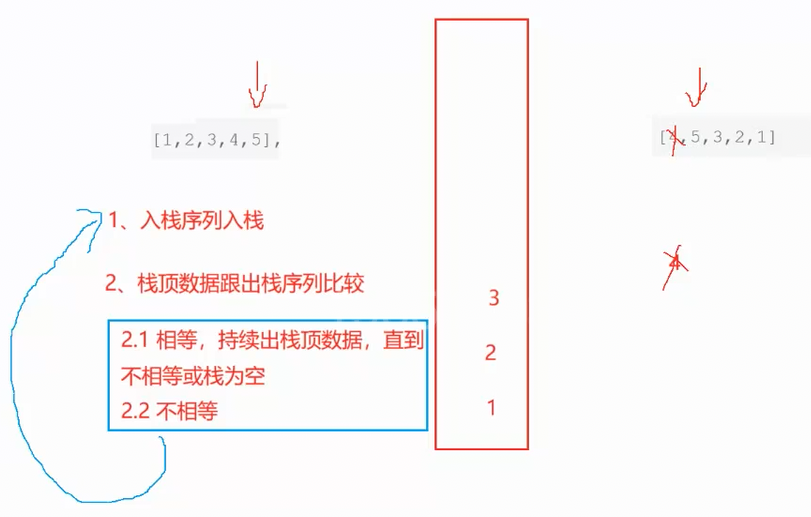
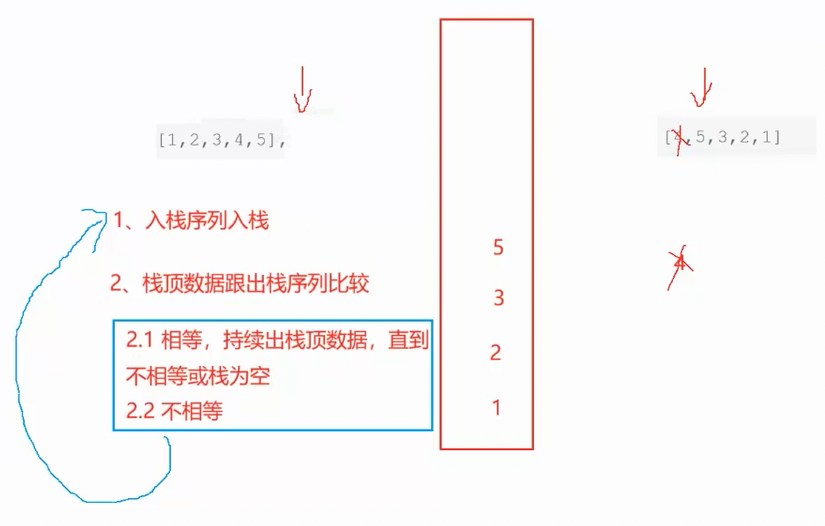
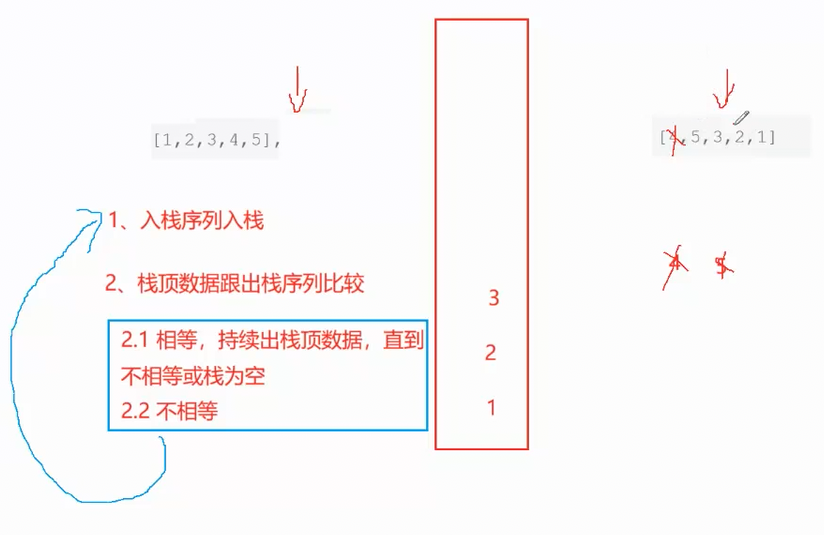
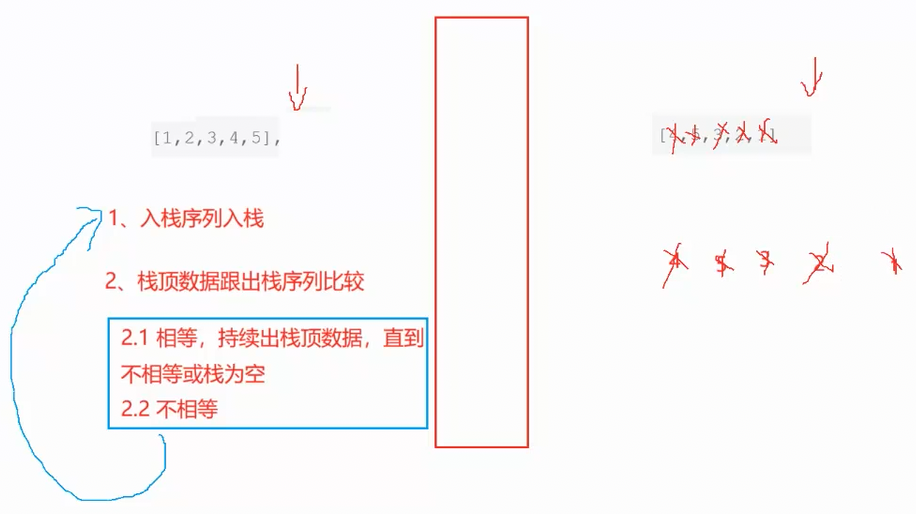
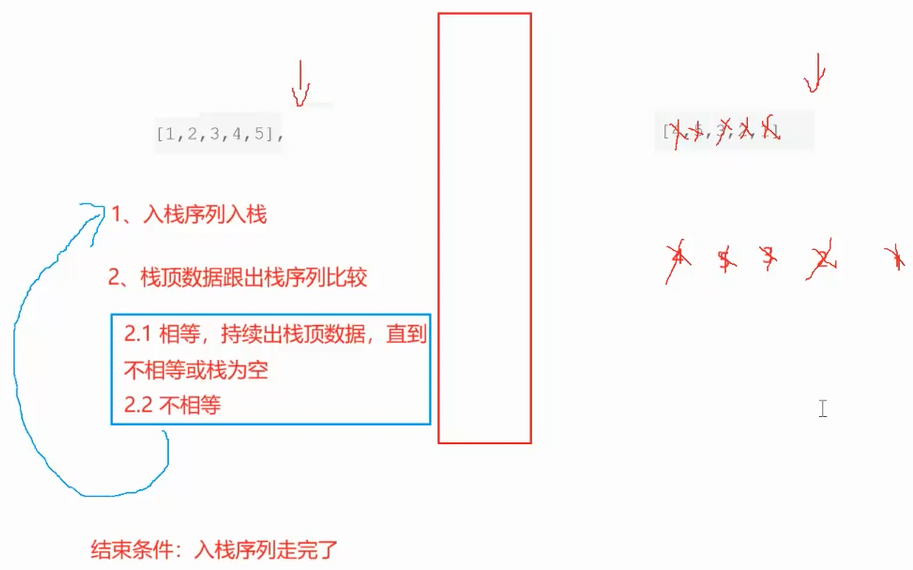
一个栈的一种压入顺序可能对应多种弹出顺序，比如图中所给样例1

[1,2,3,4,5],[4,5,3,2,1]

先压入1，2，3，4。然后弹出4，再压5，之后弹出5，再弹出3，2，1

所以说该序列就是一个合法序列

对于样例2来说

[1,2,3,4,5],[4,3,5,1,2]

先压入1，2，3，4。然后弹出4，3

再压入5，弹出5

然而接下来就不可能先弹出1了，按照结构应该先弹出2，所以该序列就是不合法的

所以核心思路就是使用一个栈来模拟这个过程

下面是合法序列的推演

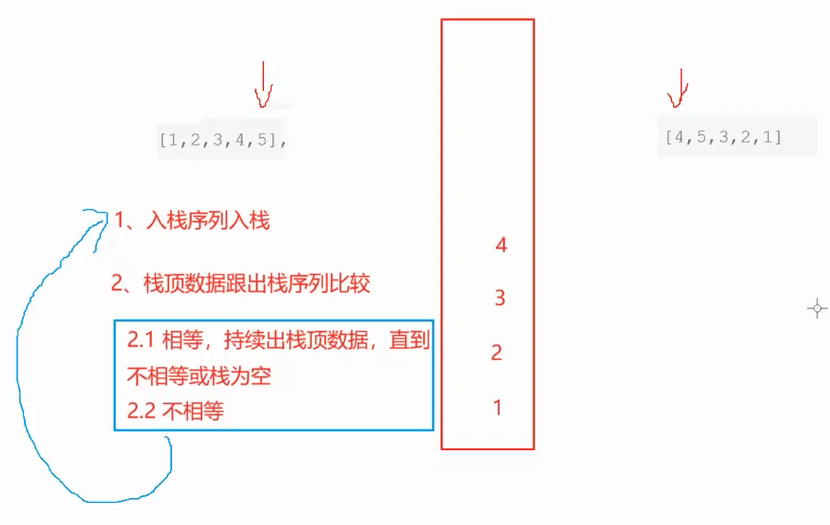
下面是不合法序列的推演

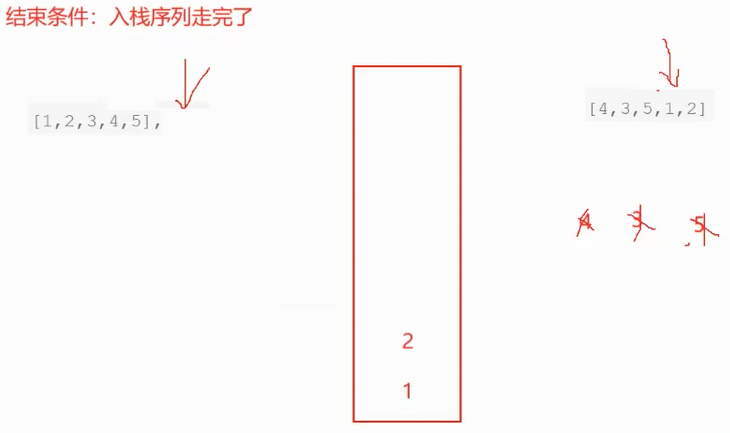
此时出栈序列还有值，栈不为空，而入栈序列走完了，所以不合法

所以合法的条件就是此时栈为空或出栈序列没有值

class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param pushV int整型vector 
     * @param popV int整型vector 
     * @return bool布尔型
     */
    bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {
        //入栈序列下标，出栈序列下标
        size_t pushi = 0, popi = 0;
        stack<int> st;
        while(pushi < pushV.size())
        {
            st.push(pushV[pushi]);
            while(!st.empty() && st.top() == popV[popi])
            {
                st.pop();
                popi++;
            }
            pushi++;
        }
        return st.empty();
    }
};

2.3 逆波兰表达式求值

逆波兰表达式求值

波兰表达式是一个波兰的逻辑学家研究的，我们平时进行计算会认为的判断运算符的优先级的，但是对于计算器或计算机就不行了，当我们输入1+2×3-4，计算器就会按照输出的顺序进行运算，那此时运算结果就会出错，所以就出现了后缀表达式来解决这个问题

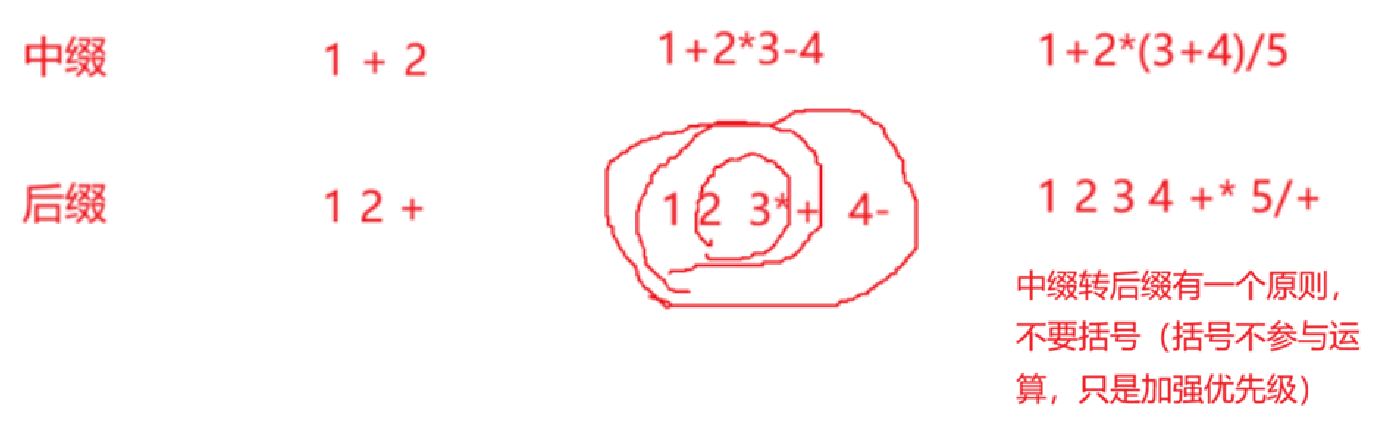
后缀表达式就是操作符紧跟着要运算的操作数，如上图：2 × 3先运算，※放在2和3的后面，运算的结果6作为一个新的操作数要进行 + 运算（+和-是同优先级的，同优先级的是前一个先运算），由于+的两个操作数一个是1一个是2×3的结果，所以+插在※后面，1+2×3的结果又是一个操作数，通过-与4进行运算，所以-插入到4的后面

这其中的规律也是有一个算法的，我后面单独出一篇文章来写

1 2 3 入栈之后，下一个遇到一个×号，接下来就要取栈顶元素进行操作数运算，接下来先取到的就是右操作数（加乘是不区分左右操作数，减除是要区分左右操作数的），操作数入栈的时候是先入左，再入右，出的时候就是先出右再出左，这是栈后进先出的结构特点

然后相乘结果入栈

接下来读到+号，再取操作数运算

把运算的结果7入栈，再把下一个操作数4入栈

以此类推，最后结果3也要入栈，最后栈中留下来的值就是运算结果

class Solution {
public:
    int evalRPN(vector<string>& tokens) {
        stack<int> st;
        //自定义类型用引用，避免拷贝
        for(auto& str : tokens)
        {
            if(str == "+" || str == "-" || str == "*" || str == "/")
            {
                //运算符
                int right = st.top();
                st.pop();
                int left = st.top();
                st.pop();
                switch(str[0])
                {
                    case '+':
                        st.push(left + right);
                        break;
                    case '-':
                        st.push(left - right);
                        break;
                    case '*':
                        st.push(left * right);
                        break;
                    case '/':
                        st.push(left / right);
                        break;
                }
            }else{
                //运算数，将字符串转换为整型
                st.push(stoi(str));
            }
        }
        return st.top();
    }
};

注意switch后面括号里的值和后面的case中的对应值只能用整型，否则会报错，字符串里面就是加减乘除，str[0]取到的是一个字符，字符是char类型，char类型也是一种整型

2.4 二叉树的层序遍历（广度优先搜索（BFS））

二叉树的层序遍历

链式二叉树算法精讲：前中后序、层序与完全二叉树判断

该题目和这篇文章使用的层序遍历的方法一样，都是通过使用一个队列来达到一个层序遍历的效果
首先将根节点保存在队列中，使队列不为空，循环判断队列是否为空，不为空取队头，将队头结点不为空的孩子结点入队列

但是该题目的输出要求是将每一层的数据单独放到二维数组的一行中去，在实际使用队列操作时

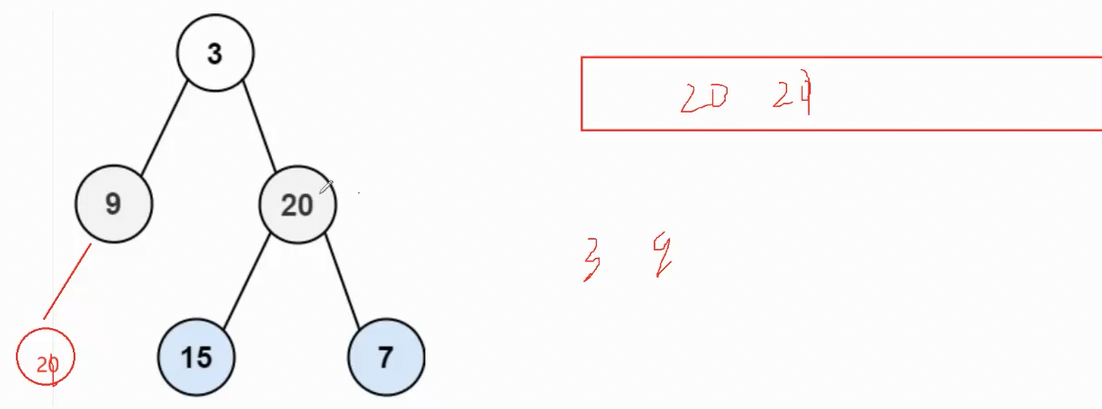
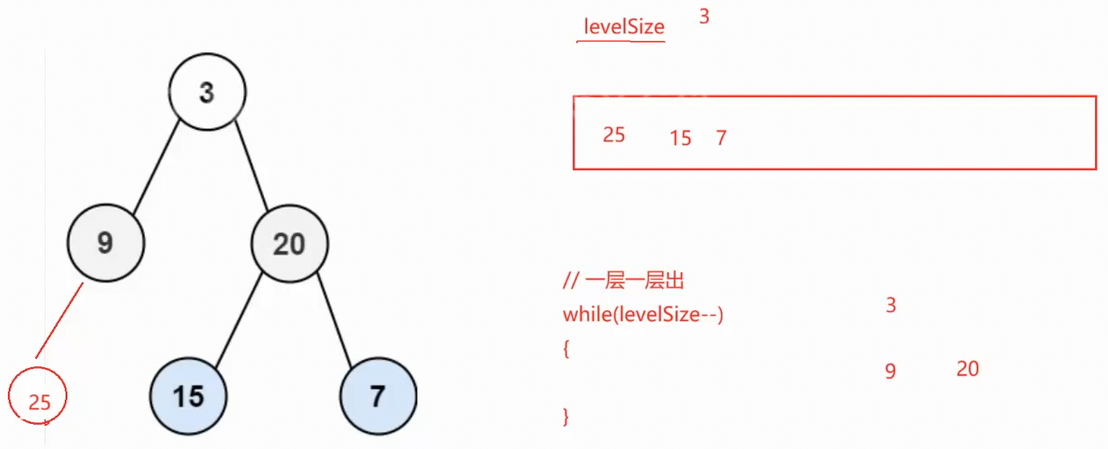
队列中的20和21是两层的数据，不好区分，所以解决办法就是增加一个变量levelSize（一层的数量）来控制

在实际入队列时先让3进去，leveSize标记为1（第一层只有一个根节点是确定的），出数据的时候用一个循环一层一层的出数据

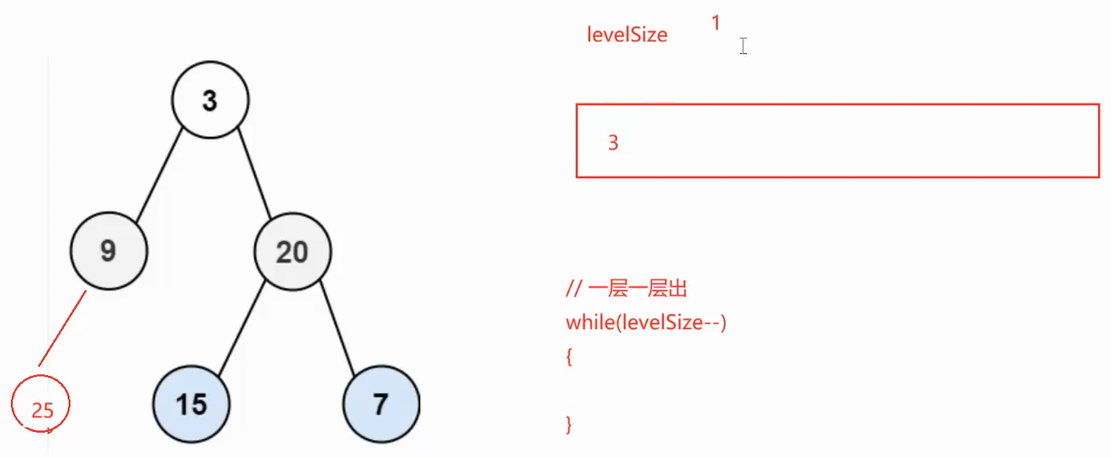
接下来出第一层， levelSize减为0，3出去之后就会把下一层带进来（层序遍历的特点就是上一层带下一层，下一层是上一层的孩子，上一层出的时候就会把下一层的孩子带进队列），此时队列的size就是下一层的数据个数

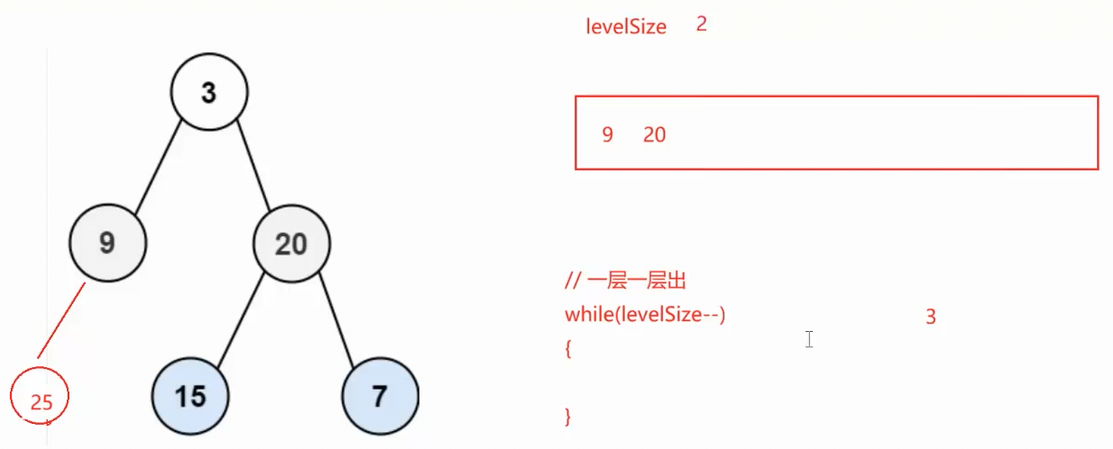
此时再出一层，第二层levelSize为2，出9和20，9带入25，20带入15和7

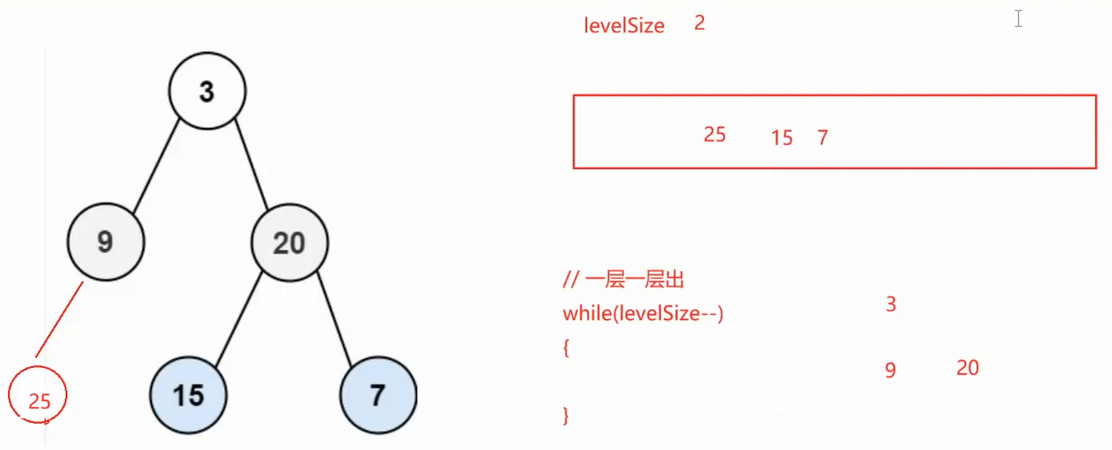
此时队列中的size就是第三层的数据个数

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        //队列中存二叉树节点的指针
        queue<TreeNode*> q;
        int levelSize = 0;
        //若根不为空
        if(root)
        {
            q.push(root);
            levelSize = 1;
        }
        vector<vector<int>> vv;
        while(!q.empty())
        {
            vector<int> v;
            while(levelSize--)
            {
                TreeNode* front = q.front();
                q.pop();
                v.push_back(front->val);

                if(front->left)
                    q.push(front->left);
                if(front->right)
                    q.push(front->right);
            }
            vv.push_back(v);
            levelSize = q.size();
        }
        return vv;
    }
};

补充一下：这里重复的vector< int > v;是没事的
vector< int > v; 定义在外层 while 循环的内层（层处理逻辑块），每一次执行到这行代码时：

1. 作用域：v的作用域仅限于「当前轮层处理的逻辑块」（即从定义处到本轮for循环结束、ret.push_back(v)完成）；
2. 生命周期：每一轮 while 循环中，v会被重新创建（栈上分配内存） → 存储当前层节点值 → 存入ret后，本轮循环结束，v的生命周期也随之结束 → 栈上内存自动释放；
3. 独立性：每一轮的v都是全新的、独立的局部变量，不会和上一轮 / 下一轮的v产生任何数据冲突（比如残留上一层的数值）。

---

结语