机器学习012:监督学习【回归算法】（对比）-- AI预测世界的“瑞士军刀”

今天我们要聊的是回归算法------这是AI世界里最实用、最基础的工具箱。

想象一下这样的场景：

你想根据广告投入，预测下个月的销售额
医生想根据病人的检查指标，判断是否有某种疾病的风险
网站想根据用户特征，预测点击广告的概率

这些看似不同的问题，其实都需要从数据中找到规律，做出预测或判断。今天我们就来认识回归算法家族的"五大明星"。

回归算法：AI的"预测引擎"

回归算法是监督学习中最重要的一类方法。什么是监督学习？就像老师教学生认字：

老师先给出很多"带答案的例题"（标注好的数据）
学生通过学习这些例题，掌握规律
然后学生就能自己认新字了（预测新数据）

回归算法主要解决两大类问题：

数值预测：预测具体的数值（比如房价、销售额）
概率预测：预测某个事件发生的可能性（比如患病概率）

让我们看看回归算法在整个AI大家庭中的位置：
机器学习监督学习无监督学习强化学习分类算法回归算法线性回归逻辑回归岭回归 Lasso回归多项式回归预测具体数值预测概率处理多重共线性自动特征选择拟合曲线关系

好了，热身结束！现在让我们一一认识这五位"预测高手"。

第一位：线性回归 ------ 简单直接的"直尺"

这位高手的特点：简单、直观、易理解

线性回归是所有回归算法中最基础、最简单的一位。它就像一个直尺，认为世界上的关系都是直线的。

生活化类比 ：

你想预测外卖送餐时间。线性回归会这样思考：

复制代码

送餐时间 = 0.5 × 距离 + 2 × 天气系数 + 10

距离越远，时间越长
天气越差，时间越长
10分钟是基础准备时间

它是如何工作的？（底层原理）

线性回归的核心是找到一条最佳拟合直线。

文字描述核心逻辑：

假设输出值（y）和输入特征（x₁, x₂...）之间是直线关系
开始时随便画一条直线
计算这条直线和所有真实数据点的"距离"（误差）
不断调整直线，让总误差最小
找到的那条"最佳直线"就是我们的模型

图示理解：
否是输入数据假设直线关系计算预测值计算误差误差最小? 调整直线参数得到最终模型

公式表示：

y=β0+β1x1+β2x2+...+βpxp+εy = β₀ + β₁x₁ + β₂x₂ + ... + βₚxₚ + εy=β0+β1x1+β2x2+...+βpxp+ε

y：要预测的值
x₁, x₂...：特征（影响因素）
β₀, β₁...：权重（每个特征的重要性）
ε：随机误差

它的局限性

只能处理线性关系：如果真实关系是曲线，它就画不准
- 为什么：就像只能用直尺画图，遇到弯曲的线条就没办法了
对异常值敏感：几个极端值就能把整条直线"拉偏"
- 为什么：就像拔河比赛，几个大力士就能改变胜负
多重共线性问题：如果特征之间高度相关，结果会不稳定
- 为什么：就像几个人说同样的话，你分不清谁的意见更重要

适合它解决的问题

最适合：

影响因素和结果之间确实是直线关系
需要快速得到初步结果
需要模型容易解释的业务场景

不适合：

影响因素和结果是复杂的曲线关系
数据中有很多异常值
特征之间高度相关

它的实际应用

房价预测
- 作用：根据面积、地段、房龄预测房价
- 公式：房价 = a×面积 + b×地段评分 + c×房龄 + d
销售额预测
- 作用：根据广告投入、促销力度预测销售额
- 帮助制定营销预算
学生学习时间与成绩关系
- 作用：分析学习时间对成绩的影响程度
- 帮助制定学习计划

第二位：逻辑回归 ------ 预测概率的"尺子"

这位高手的特点：专门预测"可能性"

虽然名字里有"回归"，但逻辑回归实际上主要用于分类问题 。它不预测具体数值，而是预测概率------某事发生的可能性有多大。

生活化类比 ：

预测明天会不会下雨。逻辑回归给出的是：

下雨的概率：73%
不下雨的概率：27%
然后我们可以设定一个阈值（比如50%），超过就判断为"会下雨"。

它是如何工作的？（底层原理）

逻辑回归的核心是S型函数，它能把任意数值压缩到0-1之间。

关键概念解释：

Sigmoid函数：一个特殊的S形曲线，能把任何数变成0到1之间的概率值
对数几率：用"发生概率/不发生概率"的对数来表示关系

文字描述核心逻辑：

先用线性回归的思路计算一个分数
把这个分数通过Sigmoid函数"挤压"成0-1之间的概率
概率接近1表示很可能发生，接近0表示不太可能发生
通常设定0.5为阈值，超过就判断为"是"

图示理解：
是否输入特征线性组合计算分数 Sigmoid函数转换得到概率值0-1 概率大于0.5? 预测为1 是/真预测为0 否/假

公式表示：

P(y=1)=1/(1+e(−z))P(y=1) = 1 / (1 + e^(-z))P(y=1)=1/(1+e(−z))

其中 z = β₀ + β₁x₁ + ... + βₚxₚ

P(y=1)：事件发生的概率
e：自然常数（约2.718）
z：线性组合的结果

它的局限性

只能处理线性边界：分类边界必须是直线（或超平面）
- 为什么：它的决策边界是由线性方程决定的
对特征相关性敏感：特征之间相关性太强会影响效果
- 为什么：就像投票时几个人意见完全一样，会扭曲结果
需要较大样本量：样本太少时效果不稳定
- 为什么：就像调研太少人，结论可能不靠谱

适合它解决的问题

最适合：

二分类问题（是/否，成功/失败等）
需要知道概率而不仅仅是分类结果
特征和结果之间是线性可分的

不适合：

多分类问题（需要改造）
复杂的非线性分类边界
特征之间存在复杂交互作用

它的实际应用

垃圾邮件识别
- 作用：判断一封邮件是不是垃圾邮件
- 给出"是垃圾邮件"的概率，比如87%
疾病风险预测
- 作用：根据检查指标，预测患病风险
- 医生可以看到具体的风险概率
信用卡欺诈检测
- 作用：判断一笔交易是否可疑
- 银行可以设定不同的风险阈值

第三位：岭回归 ------ 稳重的"调解员"

这位高手的特点：在过拟合和欠拟合之间找平衡

当特征之间存在高度相关（多重共线性）时，线性回归的结果会很不稳定。岭回归通过增加一点点约束来解决这个问题。

生活化类比 ：

几个专家给你建议，但他们意见都差不多。你不知道该听谁的。岭回归就像说：

"大家的意见我都听，但我不完全相信任何一个人，我会把大家的意见都考虑一点，但不过分依赖某个专家。"

它是如何工作的？（底层原理）

岭回归在损失函数中增加了一个惩罚项，限制系数的大小。

关键概念解释：

正则化：给模型添加约束，防止它太复杂
L2正则化：惩罚项是系数的平方和

文字描述核心逻辑：

和线性回归一样，想找最佳拟合
但加了一个条件：系数不能太大
在"拟合好数据"和"系数小"之间找平衡
通过调节λ参数控制平衡点

图示理解：
输入数据计算两个目标目标1:拟合误差小目标2:系数平方和小寻找最佳平衡点通过λ控制权重得到稳定模型

公式表示：

复制代码

损失函数 = Σ(y - ŷ)² + λ × Σβᵢ²

前半部分：拟合误差（和线性回归一样）
后半部分：惩罚项，系数平方和
λ：调节参数，控制惩罚力度

它的局限性

不进行特征选择：所有特征都保留，只是缩小系数
- 为什么：它只是让不重要的特征系数变小，但不归零
需要调节λ参数：λ选不好效果可能变差
- 为什么：惩罚太重会欠拟合，太轻又解决不了共线性
对异常值仍然敏感：虽然比线性回归稳定，但还是受影响
- 为什么：惩罚项主要解决共线性，对异常值帮助有限

适合它解决的问题

最适合：

特征之间存在高度相关（多重共线性）
所有特征都可能有贡献，不想丢弃任何特征
需要比线性回归更稳定的预测

不适合：

需要进行特征选择的场景
特征数量特别多，大部分是噪声
希望得到稀疏解（很多系数为0）

它的实际应用

经济预测
- 作用：预测GDP增长，各种经济指标高度相关
- 保留所有指标，但降低不稳定的影响
基因数据分析
- 作用：分析基因表达与疾病的关系
- 很多基因功能相似，存在共线性
股票市场分析
- 作用：预测股价，多种技术指标相关
- 稳定比极端准确更重要

第四位：Lasso回归 ------ 精明的"精简师"

这位高手的特点：自动选择重要特征

Lasso回归和岭回归类似，也添加惩罚项，但惩罚方式不同。Lasso能让不重要的特征的系数直接变成0，实现自动特征选择。

生活化类比 ：

你要去旅行，带了很多东西。Lasso就像个经验丰富的旅行家：

"这个需要，带上；那个用不上，扔掉；这个偶尔有用但太重，也不带。"

最后你只带最必要的几样东西。

它是如何工作的？（底层原理）

Lasso使用L1正则化，惩罚项是系数的绝对值之和。

关键概念解释：

L1正则化：惩罚项是系数的绝对值之和
特征选择：不重要的特征系数变为0，相当于被移除

文字描述核心逻辑：

和线性回归一样想最小化误差
但加了一个条件：所有系数的绝对值之和不能太大
这个条件会让一些不重要的系数直接变成0
实现自动选择重要特征

为什么能产生稀疏解：

数学上，L1惩罚的几何形状是"菱形"
在优化过程中，容易碰到菱形的"角"
在角上，一些坐标正好是0

图示理解：
所有特征 Lasso处理特征重要性评估重要特征不重要特征系数较大系数变为0 最终模型:只含重要特征

公式表示：

复制代码

损失函数 = Σ(y - ŷ)² + λ × Σ|βᵢ|

前半部分：拟合误差
后半部分：L1惩罚项，系数绝对值之和
λ越大，越多系数变为0

它的局限性

群组选择问题：如果有一组高度相关的特征，可能只随机选一个
- 为什么：它不知道这些特征本质相关，可能任意选一个代表
特征数>样本数时有限制：最多只能选择样本数个特征
- 为什么：数学上的限制
不稳定：数据微小变化可能导致选择不同的特征
- 为什么：边界情况可能让系数在0附近波动

适合它解决的问题

最适合：

特征数量很多，想自动选择重要特征
希望得到稀疏模型（很多系数为0）
解释性要求高，想知道哪些特征真正重要

不适合：

所有特征都可能重要，不想丢弃任何特征
高度相关的特征组需要全部保留
特征数远大于样本数且需要选很多特征

它的实际应用

基因组学特征选择
- 作用：从上万个基因中找出与疾病相关的几十个
- 极大简化模型，提高可解释性
文本分类特征选择
- 作用：从大量词汇中选择关键词汇
- 减少维度，提高效率
消费者行为分析
- 作用：从数百个消费特征中找出关键影响因素
- 帮助制定精准营销策略

第五位：多项式回归 ------ 灵活的"曲线拟合师"

这位高手的特点：用曲线捕捉复杂关系

当变量之间的关系不是直线而是曲线时，多项式回归就派上用场了。它通过添加特征的幂次项来拟合曲线。

生活化类比 ：

小孩身高随年龄增长：

0-2岁：长得快（曲线较陡）
2-12岁：匀速增长（接近直线）
12-18岁：青春期快速长高（又变陡）
18岁后：基本停止（平缓）
这需要用曲线而不是直线来描述。

它是如何工作的？（底层原理）

多项式回归本质上是线性回归的扩展，只是把特征的高次幂也作为新特征。

关键概念解释：

多项式特征：x, x², x³等作为新特征
仍用线性回归：只是特征空间扩展了

文字描述核心逻辑：

生成新的多项式特征
- 原始特征：x
- 新特征：x², x³, x⁴...
把这些新特征和原始特征一起作为输入
用线性回归方法拟合
结果是一个多项式函数

图示理解 ：

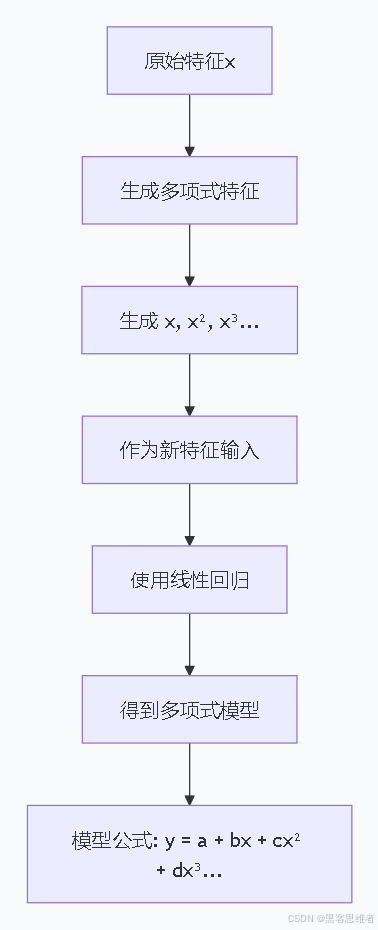
公式表示：

复制代码

y = β₀ + β₁x + β₂x² + β₃x³ + ... + βₚxᵖ + ε

x², x³...：特征的高次项
虽然是非线性关系，但对参数β仍是线性的
所以仍可用线性回归的方法求解

它的局限性

容易过拟合：阶数太高会完美拟合训练数据但泛化差
- 为什么：就像用复杂曲线连每个点，但对新点预测差
外推能力差：超出训练数据范围时预测不可靠
- 为什么：多项式在两端可能急剧上升或下降
特征维度爆炸：多特征时多项式项增长极快
- 为什么：3个特征2次多项式就有10项，3次就有20项

适合它解决的问题

最适合：

变量之间是曲线关系
数据范围有限，不需要外推
关系模式明确，知道大概是什么曲线

不适合：

需要预测训练范围之外的值
特征很多，维度会爆炸
关系非常复杂，不是简单多项式能描述

它的实际应用

物理实验曲线拟合
- 作用：拟合实验数据曲线，如弹簧伸长与力的关系
- 验证物理定律
经济增长趋势拟合
- 作用：拟合GDP增长曲线
- 分析经济增长阶段
药物剂量反应曲线
- 作用：拟合药效随剂量变化曲线
- 确定最佳用药剂量

五大回归算法对比总结

算法	核心思想	优点	缺点	最适合场景
线性回归	最佳直线拟合	简单、快速、易解释	只能处理线性关系	简单线性预测
逻辑回归	预测概率	输出概率值、用于分类	只能线性分类	二分类概率预测
岭回归	L2正则化	稳定、抗共线性	不进行特征选择	特征相关时的稳定预测
Lasso回归	L1正则化	自动特征选择、稀疏解	可能丢弃重要特征	高维特征选择
多项式回归	曲线拟合	拟合非线性关系	易过拟合、外推差	已知曲线形式的拟合

Python实践案例：房价预测大比拼

下面我们用Python实际体验这五种回归算法。我们会用同一个房价数据集，看不同算法的表现。

环境准备

python 复制代码

# 安装必要的库（如果还没安装）
# pip install numpy pandas matplotlib scikit-learn seaborn

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, PolynomialFeatures
from sklearn.linear_model import LinearRegression, LogisticRegression, Ridge, Lasso
from sklearn.metrics import mean_squared_error, r2_score, accuracy_score

# 设置中文字体和美观样式
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
sns.set_style("whitegrid")

数据准备和探索

python 复制代码

# 创建模拟的房价数据集
np.random.seed(42)  # 确保可重复性

# 生成200条数据
n_samples = 200

# 特征1：面积（平方米，50-200）
area = np.random.uniform(50, 200, n_samples)

# 特征2：房间数（1-5）
rooms = np.random.randint(1, 6, n_samples)

# 特征3：到地铁距离（公里，0.1-5）
distance = np.random.uniform(0.1, 5, n_samples)

# 特征4：房龄（年，0-50）
age = np.random.uniform(0, 50, n_samples)

# 特征5：是否学区房（0/1）
school = np.random.randint(0, 2, n_samples)

# 生成房价（万元）
# 真实关系：面积和房间数主要影响，但存在非线性
price = (0.8 * area + 
         15 * rooms + 
         -3 * distance + 
         -0.5 * age + 
         20 * school +
         0.02 * area**2 +  # 非线性项
         np.random.normal(0, 15, n_samples))  # 随机噪声

# 创建DataFrame
data = pd.DataFrame({
    '面积': area,
    '房间数': rooms,
    '地铁距离': distance,
    '房龄': age,
    '学区房': school,
    '房价': price
})

print("数据概览：")
print(f"数据形状：{data.shape}")
print("\n前5行数据：")
print(data.head())
print("\n基本统计信息：")
print(data.describe())

# 可视化特征与房价的关系
fig, axes = plt.subplots(2, 3, figsize=(15, 10))
axes = axes.flatten()

features = ['面积', '房间数', '地铁距离', '房龄', '学区房']
for i, feature in enumerate(features):
    axes[i].scatter(data[feature], data['房价'], alpha=0.6)
    axes[i].set_xlabel(feature)
    axes[i].set_ylabel('房价（万元）')
    axes[i].set_title(f'{feature} vs 房价')

# 最后一个子图显示房价分布
axes[5].hist(data['房价'], bins=30, edgecolor='black', alpha=0.7)
axes[5].set_xlabel('房价（万元）')
axes[5].set_ylabel('频次')
axes[5].set_title('房价分布')

plt.tight_layout()
plt.show()

数据预处理

python 复制代码

# 准备特征和目标变量
X = data[['面积', '房间数', '地铁距离', '房龄', '学区房']]
y = data['房价']

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

print(f"训练集大小：{X_train.shape}")
print(f"测试集大小：{X_test.shape}")

# 特征标准化（对正则化方法很重要）
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

1. 线性回归

python 复制代码

print("=" * 50)
print("1. 线性回归")
print("=" * 50)

# 创建和训练模型
lr = LinearRegression()
lr.fit(X_train_scaled, y_train)

# 预测和评估
y_pred_lr = lr.predict(X_test_scaled)
mse_lr = mean_squared_error(y_test, y_pred_lr)
r2_lr = r2_score(y_test, y_pred_lr)

print(f"均方误差（MSE）：{mse_lr:.2f}")
print(f"R²分数：{r2_lr:.3f}")
print("\n模型系数（权重）：")
for feature, coef in zip(X.columns, lr.coef_):
    print(f"  {feature}: {coef:7.3f}")
print(f"截距：{lr.intercept_:.3f}")

2. 岭回归

python 复制代码

print("\n" + "=" * 50)
print("2. 岭回归")
print("=" * 50)

# 创建和训练模型（尝试不同的alpha值）
ridge = Ridge(alpha=1.0)  # alpha就是λ
ridge.fit(X_train_scaled, y_train)

# 预测和评估
y_pred_ridge = ridge.predict(X_test_scaled)
mse_ridge = mean_squared_error(y_test, y_pred_ridge)
r2_ridge = r2_score(y_test, y_pred_ridge)

print(f"均方误差（MSE）：{mse_ridge:.2f}")
print(f"R²分数：{r2_ridge:.3f}")
print("\n模型系数（权重）：")
for feature, coef in zip(X.columns, ridge.coef_):
    print(f"  {feature}: {coef:7.3f}")
print(f"截距：{ridge.intercept_:.3f}")

# 比较与线性回归的系数变化
print("\n系数变化（岭回归 vs 线性回归）：")
for feature, coef_lr, coef_ridge in zip(X.columns, lr.coef_, ridge.coef_):
    change = coef_ridge - coef_lr
    print(f"  {feature}: {change:7.3f}")

3. Lasso回归

python 复制代码

print("\n" + "=" * 50)
print("3. Lasso回归")
print("=" * 50)

# 创建和训练模型
lasso = Lasso(alpha=0.1)  # alpha就是λ
lasso.fit(X_train_scaled, y_train)

# 预测和评估
y_pred_lasso = lasso.predict(X_test_scaled)
mse_lasso = mean_squared_error(y_test, y_pred_lasso)
r2_lasso = r2_score(y_test, y_pred_lasso)

print(f"均方误差（MSE）：{mse_lasso:.2f}")
print(f"R²分数：{r2_lasso:.3f}")
print("\n模型系数（权重）：")
for feature, coef in zip(X.columns, lasso.coef_):
    print(f"  {feature}: {coef:7.3f}")
print(f"截距：{lasso.intercept_:.3f}")

# 查看哪些特征被选择了（系数不为0）
selected_features = [feature for feature, coef in zip(X.columns, lasso.coef_) if abs(coef) > 0.001]
print(f"\nLasso选择的特征（{len(selected_features)}个）：{selected_features}")

4. 多项式回归

python 复制代码

print("\n" + "=" * 50)
print("4. 多项式回归（2次）")
print("=" * 50)

# 生成多项式特征（2次）
poly = PolynomialFeatures(degree=2, include_bias=False)
X_train_poly = poly.fit_transform(X_train_scaled)
X_test_poly = poly.transform(X_test_scaled)

print(f"原始特征数：{X_train_scaled.shape[1]}")
print(f"多项式特征数（2次）：{X_train_poly.shape[1]}")

# 使用线性回归拟合多项式特征
poly_lr = LinearRegression()
poly_lr.fit(X_train_poly, y_train)

# 预测和评估
y_pred_poly = poly_lr.predict(X_test_poly)
mse_poly = mean_squared_error(y_test, y_pred_poly)
r2_poly = r2_score(y_test, y_pred_poly)

print(f"均方误差（MSE）：{mse_poly:.2f}")
print(f"R²分数：{r2_poly:.3f}")

5. 逻辑回归（分类问题示例）

python 复制代码

print("\n" + "=" * 50)
print("5. 逻辑回归（分类问题）")
print("=" * 50)

# 创建一个分类问题：预测房价是否高于平均值
y_mean = np.mean(y)
y_class = (y > y_mean).astype(int)  # 1表示高价房，0表示低价房

# 重新划分数据
X_train_cls, X_test_cls, y_train_cls, y_test_cls = train_test_split(
    X, y_class, test_size=0.2, random_state=42
)

# 标准化
X_train_cls_scaled = scaler.fit_transform(X_train_cls)
X_test_cls_scaled = scaler.transform(X_test_cls)

# 逻辑回归模型
logistic = LogisticRegression(max_iter=1000)
logistic.fit(X_train_cls_scaled, y_train_cls)

# 预测和评估
y_pred_cls = logistic.predict(X_test_cls_scaled)
y_pred_prob = logistic.predict_proba(X_test_cls_scaled)[:, 1]  # 预测概率

accuracy = accuracy_score(y_test_cls, y_pred_cls)

print(f"准确率：{accuracy:.3f}")
print("\n模型系数（权重）：")
for feature, coef in zip(X.columns, logistic.coef_[0]):
    print(f"  {feature}: {coef:7.3f}")
print(f"截距：{logistic.intercept_[0]:.3f}")

# 显示前5个样本的预测概率
print("\n前5个测试样本的预测概率：")
for i in range(min(5, len(y_test_cls))):
    print(f"样本{i+1}: 真实类别={y_test_cls.iloc[i]}, "
          f"预测类别={y_pred_cls[i]}, "
          f"高价房概率={y_pred_prob[i]:.3f}")

结果比较和可视化

python 复制代码

print("\n" + "=" * 50)
print("五种回归算法性能比较")
print("=" * 50)

# 汇总结果
results = pd.DataFrame({
    '算法': ['线性回归', '岭回归', 'Lasso回归', '多项式回归(2次)', '逻辑回归(分类)'],
    'MSE': [mse_lr, mse_ridge, mse_lasso, mse_poly, np.nan],
    'R²': [r2_lr, r2_ridge, r2_lasso, r2_poly, np.nan],
    '准确率': [np.nan, np.nan, np.nan, np.nan, accuracy]
})

print(results.to_string(index=False))

# 可视化比较
fig, axes = plt.subplots(2, 2, figsize=(14, 10))

# 1. 预测值 vs 真实值对比
models = [('线性回归', y_pred_lr), 
          ('岭回归', y_pred_ridge),
          ('Lasso回归', y_pred_lasso),
          ('多项式回归', y_pred_poly)]

for idx, (name, y_pred) in enumerate(models):
    ax = axes[idx//2, idx%2]
    ax.scatter(y_test, y_pred, alpha=0.6)
    
    # 画完美预测线
    min_val = min(y_test.min(), y_pred.min())
    max_val = max(y_test.max(), y_pred.max())
    ax.plot([min_val, max_val], [min_val, max_val], 'r--', lw=2)
    
    ax.set_xlabel('真实房价')
    ax.set_ylabel('预测房价')
    ax.set_title(f'{name} - R²={results.loc[idx, "R²"]:.3f}')
    ax.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

# 系数比较图
fig, ax = plt.subplots(figsize=(12, 6))

x = np.arange(len(X.columns))
width = 0.2

rects1 = ax.bar(x - width*1.5, lr.coef_, width, label='线性回归')
rects2 = ax.bar(x - width/2, ridge.coef_, width, label='岭回归')
rects3 = ax.bar(x + width/2, lasso.coef_, width, label='Lasso回归')
rects4 = ax.bar(x + width*1.5, logistic.coef_[0], width, label='逻辑回归')

ax.set_xlabel('特征')
ax.set_ylabel('系数值')
ax.set_title('不同算法的特征系数比较')
ax.set_xticks(x)
ax.set_xticklabels(X.columns)
ax.legend()
ax.grid(True, alpha=0.3, axis='y')

plt.tight_layout()
plt.show()

用模型做新预测

python 复制代码

print("\n" + "=" * 50)
print("新房子预测示例")
print("=" * 50)

# 假设有一套新房子
new_house = pd.DataFrame({
    '面积': [120],
    '房间数': [3],
    '地铁距离': [1.5],
    '房龄': [10],
    '学区房': [1]
})

# 标准化
new_house_scaled = scaler.transform(new_house)

# 用不同模型预测
lr_pred = lr.predict(new_house_scaled)[0]
ridge_pred = ridge.predict(new_house_scaled)[0]
lasso_pred = lasso.predict(new_house_scaled)[0]

# 多项式特征转换
new_house_poly = poly.transform(new_house_scaled)
poly_pred = poly_lr.predict(new_house_poly)[0]

# 逻辑回归预测概率
logistic_prob = logistic.predict_proba(new_house_scaled)[0, 1]

print("新房特征：")
for feature in new_house.columns:
    print(f"  {feature}: {new_house[feature].values[0]}")
print()

print("不同模型的预测结果：")
print(f"线性回归预测房价：{lr_pred:.1f} 万元")
print(f"岭回归预测房价：{ridge_pred:.1f} 万元")
print(f"Lasso回归预测房价：{lasso_pred:.1f} 万元")
print(f"多项式回归预测房价：{poly_pred:.1f} 万元")
print(f"逻辑回归预测高价房概率：{logistic_prob:.1%}")
print(f"逻辑回归分类结果：{'高价房' if logistic_prob > 0.5 else '低价房'}")

给初学者的学习路径建议

先掌握线性回归：这是所有回归的基础，理解它才能理解其他变体
理解正则化的概念：
- 岭回归：L2正则化，让系数变小但不为0
- Lasso回归：L1正则化，让不重要系数为0
分清使用场景：
- 预测数值：线性、岭、Lasso、多项式回归
- 预测概率/分类：逻辑回归
动手实践最重要：
- 运行上面的代码
- 修改参数，观察变化
- 用自己的数据尝试
理解评估指标：
- 回归：MSE、RMSE、R²
- 分类：准确率、精确率、召回率

总结：回归算法的核心价值

回归算法是从数据中学习规律，用规律预测未来的最基础工具。

一句话概括：

线性回归：找最佳直线
逻辑回归：算发生概率
岭回归：稳定中求准确
Lasso回归：精简中抓重点
多项式回归：用曲线拟合复杂关系

无论你的目标是预测数值还是判断类别，无论你的数据是简单线性还是复杂非线性，回归算法家族都有合适的工具。选择哪种算法，取决于你的数据特点、业务需求和想要的结果形式。

记住，没有最好的算法，只有最合适的算法。希望通过今天的学习，你能：

理解每种回归算法的核心思想
知道何时该用哪种算法
能够用Python实现基本应用

回归算法是AI世界的基石，掌握它们，你就打开了预测分析的大门。祝你学习愉快，探索无限！