LLM参数: Temperature 与 Top-p解析

引言

大家好！平常在大模型的使用中，同一句话的输入，同一的大模型的输出都会不同。那么为什么会这样呢？是什么导致了这样的随机性呢？今天我们来讲讲LLM的参数：Temperature 与 Top-p

当我们调用 GPT API 时，我们往往把模型当成一个黑盒：输入提示词（Prompt），吐出回答。但决定这个回答是"严谨的逻辑推导"还是"天马行空的创意写作"，很大程度上取决于两个参数：Temperature（温度） 和 Top-p（核采样） 。

如果不理解这两个参数，你就只是在使用模型；理解了它们，你才能真正控制模型

Temperature (温度) 是什么

简单来说，Temperature 控制模型在生成下一个词时的"大胆程度"。

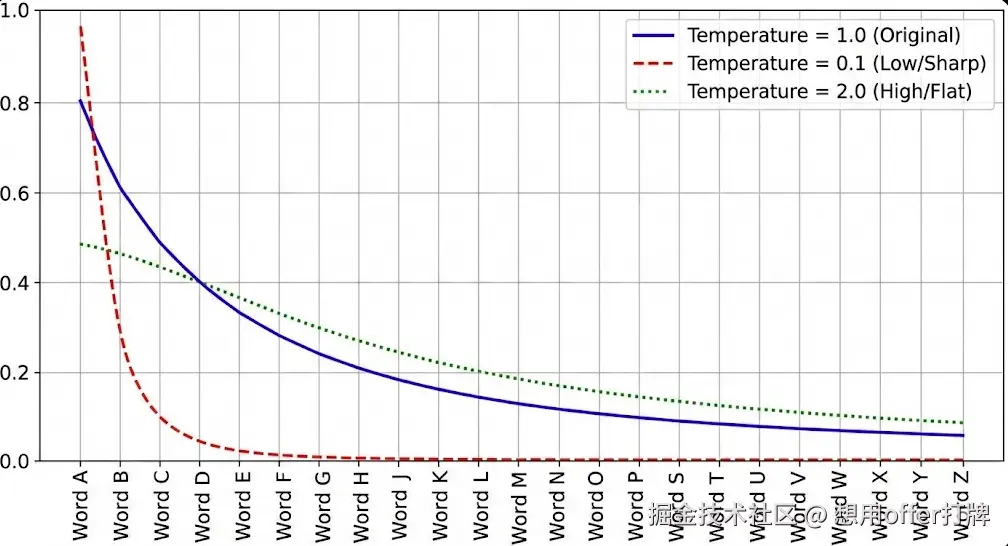
在技术底层，模型预测下一个词时，会给词表中的每个词分配一个概率。Temperature 实际上是用来缩放这些概率数值的

低温度（< 1，如 0.1 - 0.3）：让模型更"保守 / 严谨"
- 原理： 它会拉大高概率词和低概率词之间的差距。原本概率高的词，现在的概率会变得极高；原本概率低的词，几乎被忽略。
- 效果： 输出非常稳定、确定性强，几乎总是选择最正确的那个词。
- 适用场景： 代码生成、数学解题、事实性问答、数据提取。
高温度（> 1，如 0.8 - 1.5+）：让模型更"发散 / 疯狂"
- 原理： 它会缩小概率差距，让概率分布变"平"。原本概率较低的生僻词，现在也有了被选中的机会。
- 效果： 输出更多样化、更有创意，但可能会出现胡言乱语（幻觉）或语法错误。
- 适用场景： 创意写作、头脑风暴、写诗、聊天机器人。

比喻： 低温就像一个即使喝醉了也只会背乘法口诀表的严谨会计。

高温就像一个喝了酒的诗人，虽然可能写出惊世之作，但也可能不知所云

Top-p (核采样)

Top-p 是另一种控制随机性的方法，但它的逻辑和 Temperature 不同。

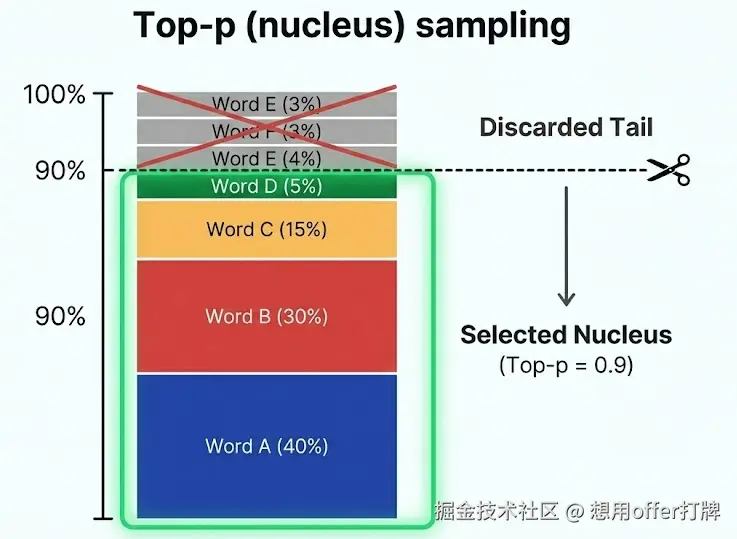
含义： Top-p 设定了一个累积概率阈值 。模型只会在累积概率达到 <math xmlns="http://www.w3.org/1998/Math/MathML"> p p </math>p 的那些候选词里进行选择，切掉尾部那些概率极低的词。
例子： 假设 <math xmlns="http://www.w3.org/1998/Math/MathML"> p = 0.9 p = 0.9 </math>p=0.9 (即 90%)。
- 模型会把候选词按概率从高到低排列。
- 它取出前几个词，直到这些词的概率加起来超过 90%。
- 剩下的所有词（也就是那 10% 的长尾词）直接被扔掉，绝对不会被选中

两者的区别

虽然它们结果都能控制多样性，但手段不同：

特性	Temperature (温度)	Top-p (核采样)
操作方式	改变概率分布的形状（变尖或变平）。	切掉尾巴，保留头部的词。
对词库的影响	理论上所有词都还有机会被选中，只是概率变了。	排名靠后的词直接被"一刀切"出局，没机会了。
直观理解	调整"胆量"。	调整"候选池范围"。

机制原理------概率的博弈

要理解它们是如何工作的，必须先理解 LLM 是怎么生成文本的。

大模型本质上是一个"下一个词预测器" （Next Token Predictor）。当输入 "天空是" 时，模型并不会直接输出 "蓝色的"，而是会输出整个词表中每个词的原始得分（Logits）。

经过转换后，我们得到一个概率分布，例如：

蓝色的: 60%
灰色的: 25%
红色的: 5%
绿色的: 1%
...（剩下几万个词分摊剩余概率）

这时候，采样策略（Sampling Strategy） 登场了。如果每次都只选概率最大的那个词（Greedy Decoding），生成的文章会极其死板且容易陷入循环。我们需要引入随机性，而 Temperature 和 Top-p 就是干预这个概率分布的手段

深度剖析------数学视角

作为后端开发，我们来看看底层的数学逻辑。

1. Temperature：重塑 Softmax 分布

模型输出的原始数值叫 Logits ( <math xmlns="http://www.w3.org/1998/Math/MathML"> z i z_i </math>zi)。在转化为概率 ( <math xmlns="http://www.w3.org/1998/Math/MathML"> P i P_i </math>Pi) 之前，会经过一个带温度 <math xmlns="http://www.w3.org/1998/Math/MathML"> T T </math>T 的 Softmax 函数：

<math xmlns="http://www.w3.org/1998/Math/MathML"> P i = exp ⁡ ( z i / T ) ∑ j exp ⁡ ( z j / T ) P_i = \frac{\exp(z_i / T)}{\sum_j \exp(z_j / T)} </math>Pi=∑jexp(zj/T)exp(zi/T)

请注意 <math xmlns="http://www.w3.org/1998/Math/MathML"> T T </math>T 在分母上的作用：

当 <math xmlns="http://www.w3.org/1998/Math/MathML"> T < 1 T < 1 </math>T<1 (如 0.1) 时：
- Logits 被放大。原本大的数值变得极大，小的数值变得极小。
- 结果：概率分布变得尖锐 (Peaked) 。60% 的概率可能变成 99%，模型几乎必然选择它。
当 <math xmlns="http://www.w3.org/1998/Math/MathML"> T > 1 T > 1 </math>T>1 (如 2.0) 时：
- Logits 被缩小。所有数值都趋向于 0，而 <math xmlns="http://www.w3.org/1998/Math/MathML"> e 0 = 1 e^0 = 1 </math>e0=1。
- 结果：概率分布变得平坦 (Flattened) 。60% 和 5% 的差距被缩小，低概率词被选中的机会大幅增加。

2. Top-p (Nucleus Sampling)：动态截断

Temperature 改变了概率的形状，但没有剔除任何词。理论上，即便 <math xmlns="http://www.w3.org/1998/Math/MathML"> T T </math>T 很低，极低概率的词（如"天空是吃"）仍有非零概率被选中。

Top-p 则是通过截断来解决问题。

它将候选词按概率从高到低排序，然后从头开始累加概率，直到总和达到 <math xmlns="http://www.w3.org/1998/Math/MathML"> p p </math>p（例如 0.9）。

场景 A（确定性高） ：
- 预测："中国的首都是..."
- 候选：北京(99%)。
- Top-p (0.9) 逻辑：取"北京"一个词，概率就够了。
- 结果：候选池只有 1 个词。
场景 B（开放性高） ：
- 预测："今天晚上我打算吃..."
- 候选：火锅(20%)、烧烤(15%)、面条(10%)...
- Top-p (0.9) 逻辑：需要把前 10-20 个食物加起来才凑够 0.9。
- 结果：候选池有 20 个词。

Top-p 的精髓在于"动态" ：它根据模型对下一个词的确定程度，自动调整候选池的大小。比传统的 Top-k（固定选前 k 个）更智能

实战策略

在实际开发（如调用 OpenAI API）时，这两个参数通常是配合使用的。

通常的执行顺序是：

模型输出 Logits。
应用 Temperature 缩放 Logits（改变分布形状）。
应用 Top-p 截断尾部（剔除离谱选项）。
在剩余的词中进行随机采样。

针对不同任务的参数推荐：

任务类型	推荐设置	理由
代码生成 / 数学解题	Temp: 0 - 0.2 Top-p: 0.1	代码对语法和逻辑要求极高，不需要"创意"，任何随机性都可能导致 Bug。
知识问答 / 事实提取	Temp: 0.3 - 0.5 Top-p: 0.8	需要回答准确，但允许在表达方式上有一点点自然的变化，显得不那么像机器人。
创意写作 / 营销文案	Temp: 0.8 - 1.0 Top-p: 0.9	需要模型跳出常规搭配（如"五彩斑斓的黑色"），高温度能激发意想不到的组合。
头脑风暴 / 角色扮演	Temp: 1.0+ Top-p: 0.95	鼓励模型发散思维，即便偶尔出现一点不连贯也可以接受。

开发者的避坑指南

尽量不要同时把两个参数都调到极端。 比如 Temp=1.5 且 Top-p=0.1，这会让模型处于精神分裂状态：一方面想发散（Temp），一方面又被强行按住（Top-p）。
调试优先调 Temperature。 它是影响最全局的参数。Top-p 更像是用来"兜底"的，防止高温状态下模型彻底崩坏。
确定性任务直接锁死。 如果你在做基于文档的 RAG（检索增强生成），为了保证答案忠实于原文，直接把 Temperature 设为 0 是最稳妥的

总结

Temperature 是"整形师"，它拉伸或压缩概率分布，决定模型是保守还是激进。
Top-p 是"保安"，它划定一个动态的安全圈，把那些概率极低的不靠谱选项拒之门外。

理解了这两个参数，你就掌握了通往大模型潜意识的钥匙