
本文给出当前前沿研究的课题推荐,基于大量的数据整合、识别、归纳和一些个人的想法。试图在导航、定位的方向研究中提供有价值的研究问题,为项目选题奠定基础。个人观点,仅供参考,也欢迎大家共同讨论。
文章目录
- 课题介绍
-
- [小波变换(Wavelet Transform)](#小波变换(Wavelet Transform))
- 互相关(Cross-correlation)
- 快速傅里叶变换(FFT)
- 卡尔曼滤波
- 融合策略
- MATLAB仿真示例
课题介绍
小波变换(Wavelet Transform)
- 提供时频局部化分析能力,适合处理非平稳信号
- 可用于去噪、特征提取和多尺度分析
- 在轨迹估计中常用于传感器数据预处理
连续小波变换(CWT)定义:
W x ( a , b ) = 1 ∣ a ∣ ∫ − ∞ ∞ x ( t ) , ψ ∗ ! ( t − b a ) , d t W_x(a,b) = \frac{1}{\sqrt{|a|}} \int_{-\infty}^{\infty} x(t),\psi^*!\left(\frac{t-b}{a}\right),dt Wx(a,b)=∣a∣ 1∫−∞∞x(t),ψ∗!(at−b),dt
其中
- a a a为尺度因子(控制频率分辨率)
- b b b为平移因子(控制时间定位)
- ψ ( ⋅ ) \psi(\cdot) ψ(⋅)为母小波函数
离散小波变换(DWT)多尺度分解:
x ( t ) = ∑ k c J , k , ϕ J , k ( t ) x(t) = \sum_{k} c_{J,k},\phi_{J,k}(t) x(t)=k∑cJ,k,ϕJ,k(t)
∑ j = 1 J ∑ k d j , k , ψ j , k ( t ) \sum_{j=1}^{J}\sum_{k} d_{j,k},\psi_{j,k}(t) j=1∑Jk∑dj,k,ψj,k(t)
其中 c J , k c_{J,k} cJ,k 和 d j , k d_{j,k} dj,k分别表示近似系数与细节系数。
互相关(Cross-correlation)
- 衡量两个信号之间的相似性和时间延迟
- 用于多传感器数据融合和信号匹配
- 可以检测轨迹中的周期性模式
连续互相关函数:
R x y ( τ ) = ∫ − ∞ ∞ x ( t ) , y ( t + τ ) , d t R_{xy}(\tau) = \int_{-\infty}^{\infty} x(t),y(t+\tau),dt Rxy(τ)=∫−∞∞x(t),y(t+τ),dt
离散互相关形式:
R x y [ k ] = ∑ n x [ n ] ; y [ n + k ] R_{xy}[k] = \sum_{n} x[n];y[n+k] Rxy[k]=n∑x[n];y[n+k]
时间延迟估计:
τ ^ = arg max τ ; R x y ( τ ) \hat{\tau} = \arg\max_{\tau} ; R_{xy}(\tau) τ^=argτmax;Rxy(τ)
该估计常用于多传感器时间同步与运动状态关联。
快速傅里叶变换(FFT)
- 将时域信号转换到频域进行分析
- 识别信号中的主要频率成分
- 用于滤波和频域特征提取
离散傅里叶变换(DFT):
X ( k ) = ∑ n = 0 N − 1 x ( n ) , e − j 2 π N k n , k = 0 , 1 , ... , N − 1 X(k) = \sum_{n=0}^{N-1} x(n),e^{-j\frac{2\pi}{N}kn}, \quad k = 0,1,\dots,N-1 X(k)=n=0∑N−1x(n),e−jN2πkn,k=0,1,...,N−1
功率谱密度(PSD):
P ( k ) = 1 N ∣ X ( k ) ∣ 2 P(k) = \frac{1}{N}\left|X(k)\right|^2 P(k)=N1∣X(k)∣2
FFT 通过降低计算复杂度,将 DFT 的计算量从
O ( N 2 ) ; → ; O ( N log N ) \mathcal{O}(N^2) ;\rightarrow; \mathcal{O}(N\log N) O(N2);→;O(NlogN)
使其适合实时轨迹与传感器信号处理。
卡尔曼滤波
卡尔曼滤波是一种递归最优估计算法,特别适合轨迹跟踪:
状态方程:
x(k) = A·x(k-1) + B·u(k) + w(k)观测方程:
z(k) = H·x(k) + v(k)其中:
- x(k):状态向量(位置、速度等)
- z(k):观测向量
- w(k)、v(k):过程噪声和观测噪声
核心步骤:
- 预测:基于运动模型预测下一状态
- 更新:利用观测数据修正预测
融合策略
信号处理 + 卡尔曼滤波的典型应用:
- 预处理:使用小波/FFT去除传感器噪声
- 特征提取:通过互相关分析多传感器数据
- 状态估计:卡尔曼滤波器融合处理后的数据
- 后处理:平滑和优化轨迹
MATLAB仿真示例
各方法的优势与适用场景
| 方法 | 优势 | 适用场景 |
|---|---|---|
| 小波变换 | 时频局部化,多尺度分析 | 非平稳信号,突变检测 |
| FFT滤波 | 计算效率高,频域直观 | 周期性运动,频率选择性滤波 |
| 互相关 | 信号匹配,时延估计 | 多传感器融合,模式识别 |
| 卡尔曼滤波 | 最优递归估计,实时性好 | 动态系统状态估计 |
部分运行结果
轨迹估计综合仿真:
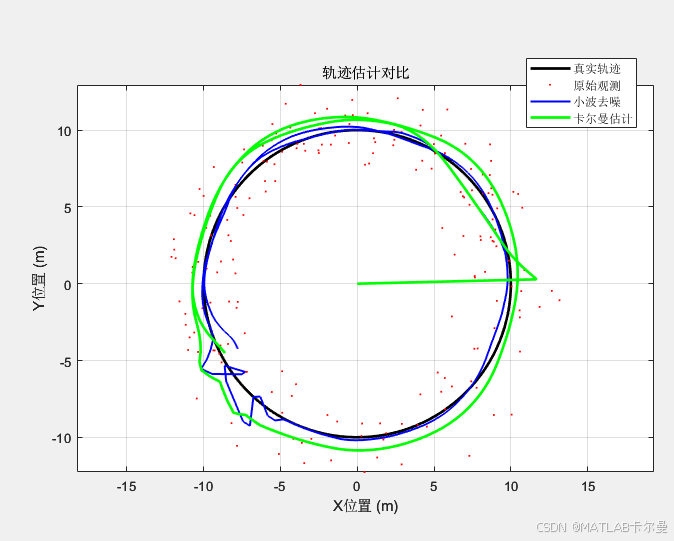
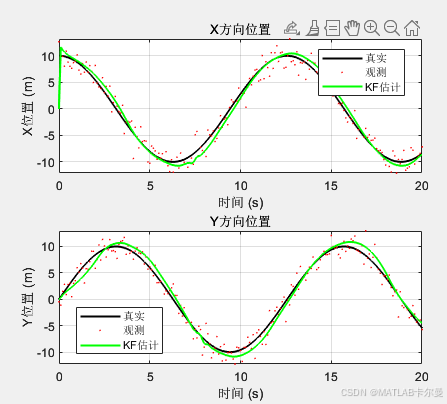
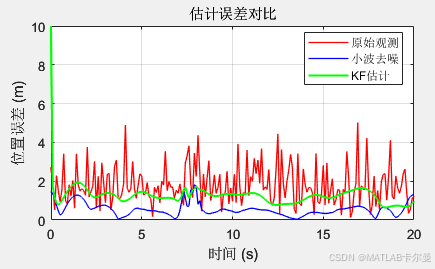
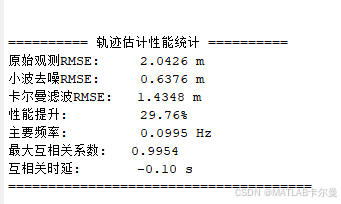
如有相关代码的定位、讲解等,可联系我