
🔥小龙报:个人主页
🎬作者简介:C++研发,嵌入式,机器人方向学习者
❄️个人专栏:《算法通关指南》
✨ 永远相信美好的事情即将发生

文章目录
- 前言
- 一、双指针
- 二、双指针经典算法题
-
- [2.1 唯一的雪花](#2.1 唯一的雪花)
- [2.2 逛画展](#2.2 逛画展)
-
- [2.2.1 题目](#2.2.1 题目)
- [2.2.2 算法原理](#2.2.2 算法原理)
- [2.2.3 代码](#2.2.3 代码)
-
- [2.2.3.1 情况一](#2.2.3.1 情况一)
- [2.2.3.2 情况二](#2.2.3.2 情况二)
- [2.2.3.3 情况三](#2.2.3.3 情况三)
- [2.3 字符串](#2.3 字符串)
-
- [2.3.1 题目](#2.3.1 题目)
- [2.3.2 算法原理](#2.3.2 算法原理)
- [2.3.3 代码](#2.3.3 代码)
- [2.4 丢手绢](#2.4 丢手绢)
-
- [2.4.1 题目](#2.4.1 题目)
- [2.4.2 算法原理](#2.4.2 算法原理)
- [2.4.3 代码](#2.4.3 代码)
- 总结与每日励志
前言
本专栏聚焦算法题实战,系统讲解算法模块:以《c++编程》,《数据结构和算法》《基础算法》《算法实战》 等几个板块以题带点,讲解思路与代码实现,帮助大家快速提升代码能力。
ps:本章节题目分两部分,比较基础笔者只附上代码供大家参考,其他的笔者会附上自己的思考和讲解,希望和大家一起努力见证自己的算法成长
一、双指针
双指针算法有时候也叫尺取法或者滑动窗口,是⼀种优化暴力枚举策略的手段:
• 当我们发现在两层for循环的暴力枚举过程中,两个指针是可以不回退的,此时我们就可以利用两个指针不回退的性质来优化时间复杂度。
• 因为双指针算法中,两个指针是朝着同⼀个方向移动的,因此也叫做同向双指针。
注意:希望大家在学习该算法的时候,不要只是去记忆模板,⼀定要学会如何从暴力解法优化成双指针算法。不然往后遇到类似题目,你可能压根都想不到用双指针去解决。
二、双指针经典算法题
2.1 唯一的雪花
2.1.1题目
链接:唯一的雪花
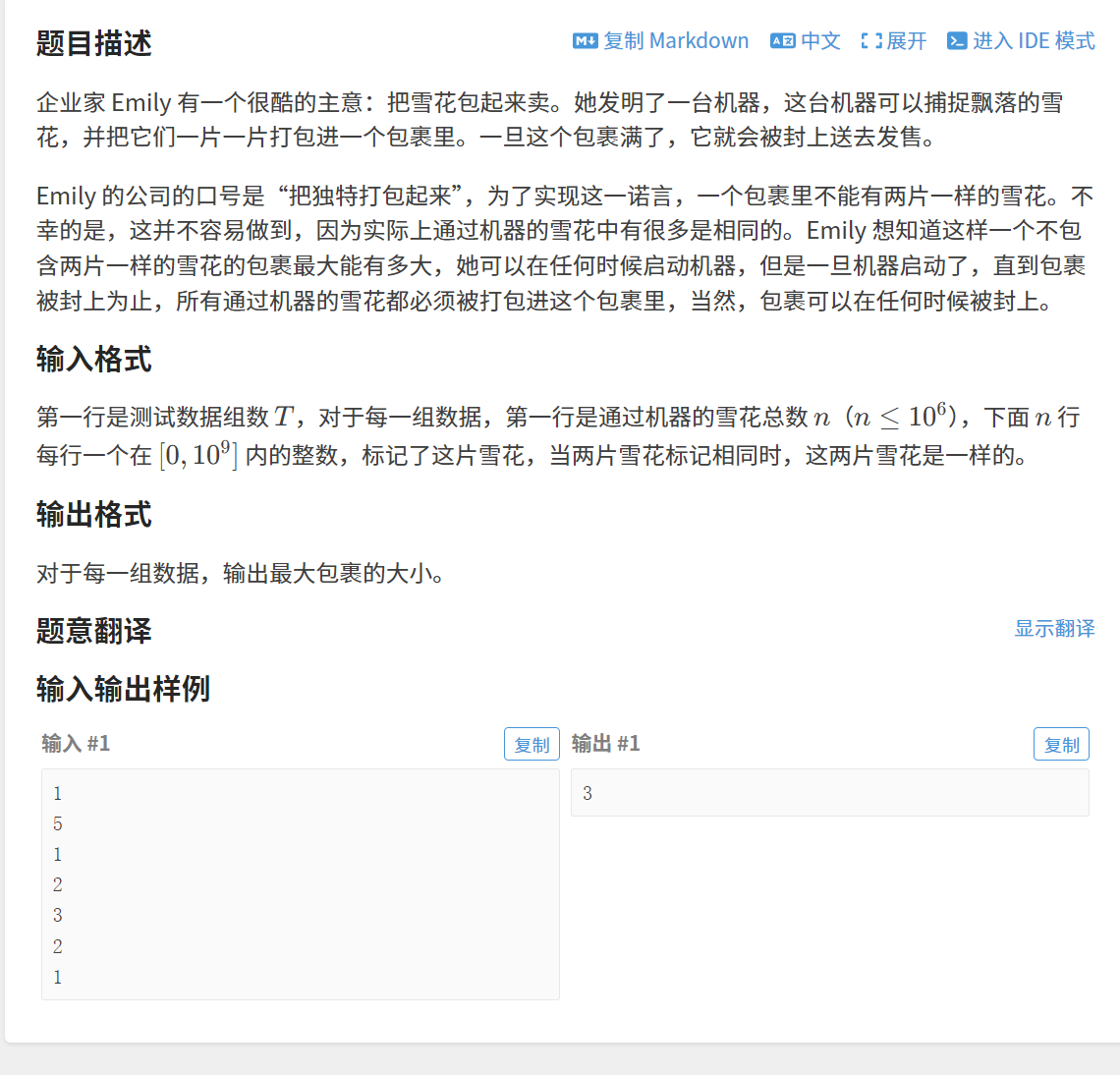
2.1.2 算法原理
我们「暴力枚举」的过程中,固定⼀个起点位置left,然后之后right向后遍历时。当right第⼀次扫描到⼀个位置,使[left,right]这个区间「出现重复字符」,此时我们会发现:
• right 无需再向后遍历,因为继续向后走区间窗口也是「不合法」的;
• left向后移动⼀格之后,right 指针也不用回退,因为我们已经维护出来[left,right]区间的信息,并且以left + 1 为起点的最优解一定不会比left为起点的好
当我们发现暴力枚举的「两个指针不回退」时,就可以用「滑动窗口」优化:
(1)进窗口:right 位置元素记录到统计次数的哈希表中;
(2)判断:当哈希表中right 位置的值出现超过1 次之后,窗口内子串不合法;
(3)出窗口:让left 所指位置的元素在哈希表中的次数减一;
(4)更新结果:判断结束之后,窗口合法,此时更新窗口的大小。
技巧: (1)哈希表可以使用STL或者使用数组模拟一个哈希效果 (2)依照题意可能在判断条件内也可能在判断条件外
2.1.3代码
c
#include <iostream>
#include <unordered_map>
using namespace std;
const int N = 1e6 + 10;
int a[N];
int main()
{
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
int l = 1, r = 1;
unordered_map<int, int> mp; // 维护窗?内所有元素出现的次数
int ret = 1;
while (r <= n)
{
mp[a[r]]++; //进窗口
while (mp[a[r]] > 1) //判断---窗口不合法的情况
{
mp[a[l++]]--;
}
ret = max(ret, r - l + 1); //更新结果
r++;
}
cout << ret << endl;
}
return 0;
}2.2 逛画展
2.2.1 题目
链接:逛画展

2.2.2 算法原理
(1)进窗口:right位置元素记录到统计次数的哈希表中,如果次数是0变1 ,说明窗口内多了「⼀种」字符,记录⼀下;
(2)判断:当窗口内字符种类等于m 时,窗口合法,right 停止右移,接下来需要出窗口;
(3)出窗口:让left所指位置的元素在哈希表中的次数减⼀,如果次数是1 变0 ,说明窗口内少了「⼀种」字符,记录⼀下;
(4)更新结果:在判断成⽴时,窗⼝合法,此时更新窗口的大小
综上 :变引出此题答案的多种处理方式也是笔者在做此题遇到的一些坑点分享给大家
(1) 因为此题要输出区间的左右下标故第一种想法便是用两个变量x和y去记录但初始化会遇到怎么样去赋初值这是会影响结果的:如果使用一个ret来记入结果:
第一种情况:ret = n那么x等于1,y = n;否则在极端条件下当区间确实是包含全部时最后的结果会出错
第二种情况:ret = 一个很大的数(此题要取最优的最短区间)故x和y赋任何值都可以
(2)第三种情况:仅使用一个变量x记录区间的头,使用x + ret - 1来直接算出第二个值(最推荐这种方式可以避免很多边界情况)
2.2.3 代码
2.2.3.1 情况一
c
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N];
int n, m;
int kind; //当前窗口不同画师量
int mp[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> a[i];
int l = 1, r = 1;
int ret = n; //存储最短窗口
int begin = 1;
int end = n;
while (r <= n)
{
if (mp[a[r]]++ == 0) //进窗口
kind++;
while (kind == m) //判断
{
if (ret > r - l + 1) //更新结果
{
ret = r - l + 1;
begin = l;
end = r;
}
if (mp[a[l++]]-- == 1) //出窗口
kind--;
}
r++;
}
cout << begin << " " << end << endl;
return 0;
}2.2.3.2 情况二
c
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N];
int n, m;
int kind; //当前窗口不同画师量
int mp[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> a[i];
int l = 1, r = 1;
int ret = 1e7; //存储最短窗口
int begin = 1;
int end = 1;
while (r <= n)
{
if (mp[a[r]]++ == 0) //进窗口
kind++;
while (kind == m) //判断
{
if (ret > r - l + 1) //更新结果
{
ret = r - l + 1;
begin = l;
end = r;
}
if (mp[a[l++]]-- == 1) //出窗口
kind--;
}
r++;
}
cout << begin << " " << end << endl;
return 0;
}2.2.3.3 情况三
c
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N];
int n, m;
int kind; //当前窗口不同画师量
int mp[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> a[i];
int l = 1, r = 1;
int ret = n; //存储最短窗口
int begin = 1;
while (r <= n)
{
if (mp[a[r]]++ == 0) //进窗口
kind++;
while (kind == m) //判断
{
if (ret > r - l + 1) //更新结果
{
ret = r - l + 1;
begin = l;
}
if (mp[a[l++]]-- == 1) //出窗口
kind--;
}
r++;
}
cout << begin << " " << begin + ret - 1 << endl;
return 0;
}2.3 字符串
2.3.1 题目
链接:字符串
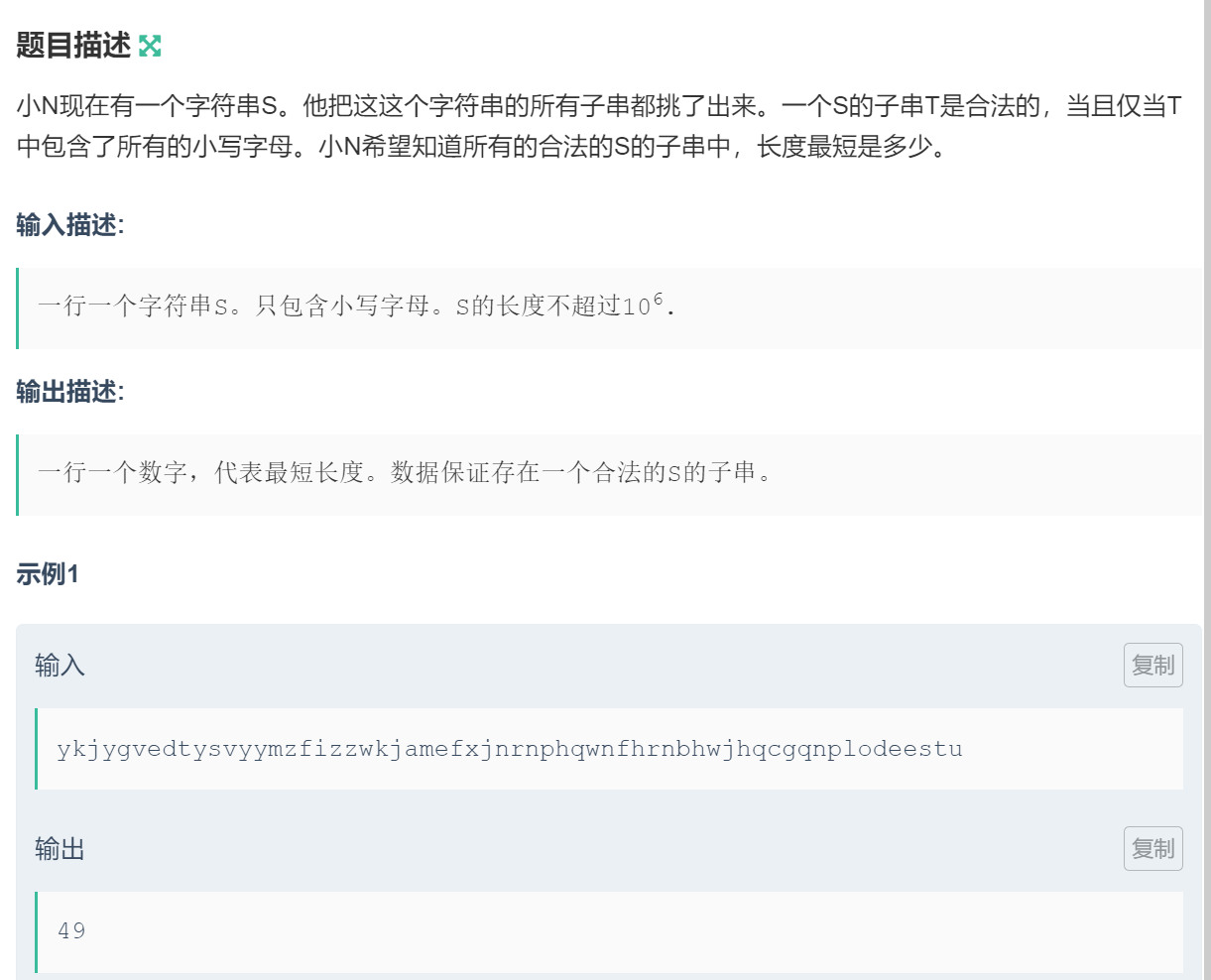
2.3.2 算法原理
定义一个变量kind记录当前窗口内统计到字符种类
(1)进窗口:right位置元素记录到统计次数的哈希表中,如果次数是0 变1 ,说明窗口内多了「⼀种」字符,记录⼀下;
(2)判断:当窗口内字符种类等于m 时,窗口合法,right 停止右移(寻找到当前情况的最优解),接下来需要出窗口;
(3)出窗口:让left 所指位置的元素在哈希表中的次数减一,如果次数是1 变0 ,说明窗口内少了「⼀种」字符,记录⼀下;
(4)更新结果:在判断成立时,窗口合法,此时更新窗口大小
2.3.3 代码
c
#include <iostream>
using namespace std;
string s;
int mp[350]; // 统计每个⼩写字符出现的次数
int kind; //窗口的元素种类
int main()
{
cin >> s;
int l = 0, r = 0;
int ret = 1e7;
while (r < s.size())
{
if (mp[s[r]]++ == 0)
kind++;
while (kind == 26)
{
ret = min(ret, r - l + 1);
if (mp[s[l++]]-- == 1)
kind--;
}
r++;
}
cout << ret << endl;
return 0;
}2.4 丢手绢
2.4.1 题目
链接:丢手绢
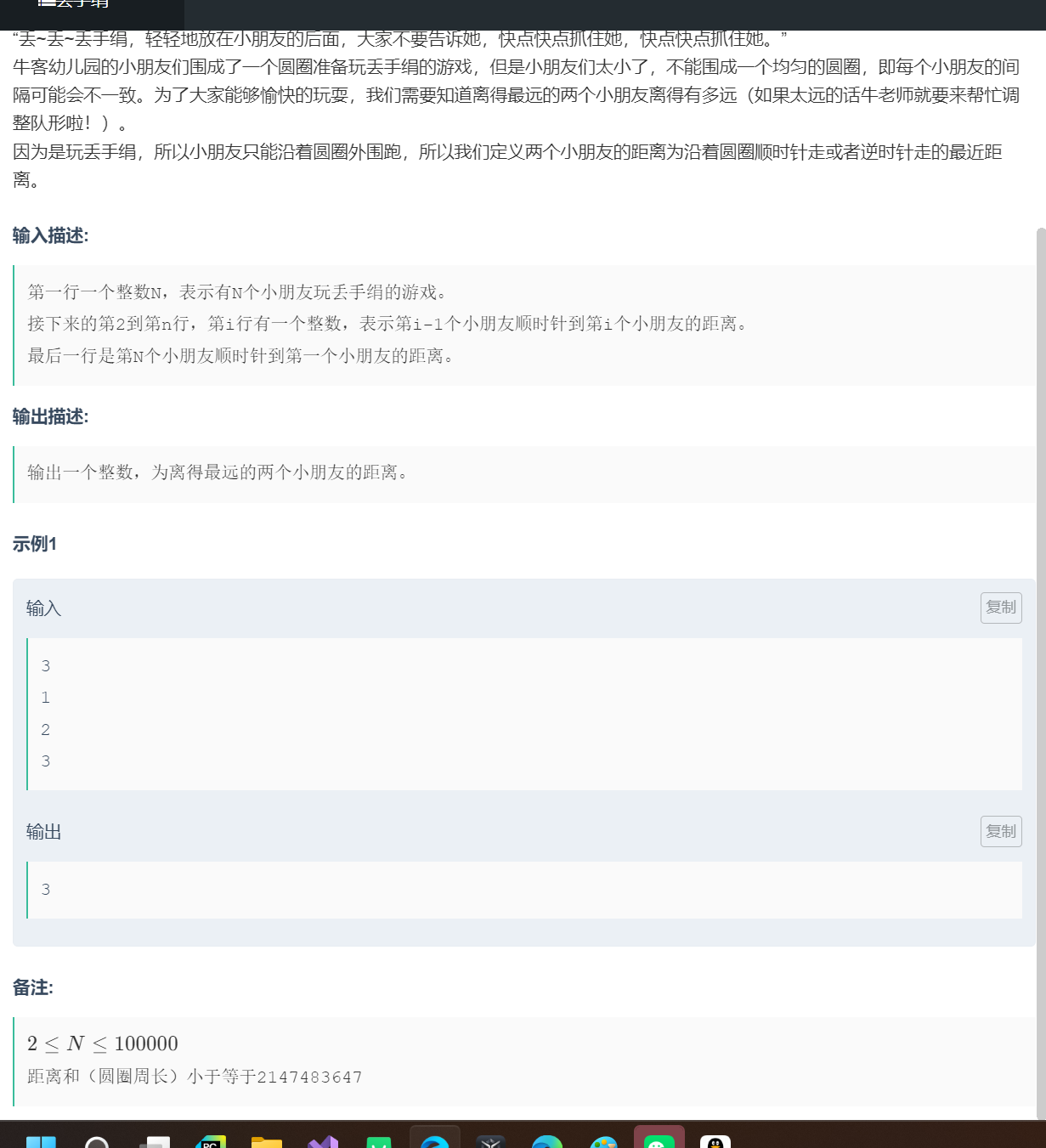
2.4.2 算法原理
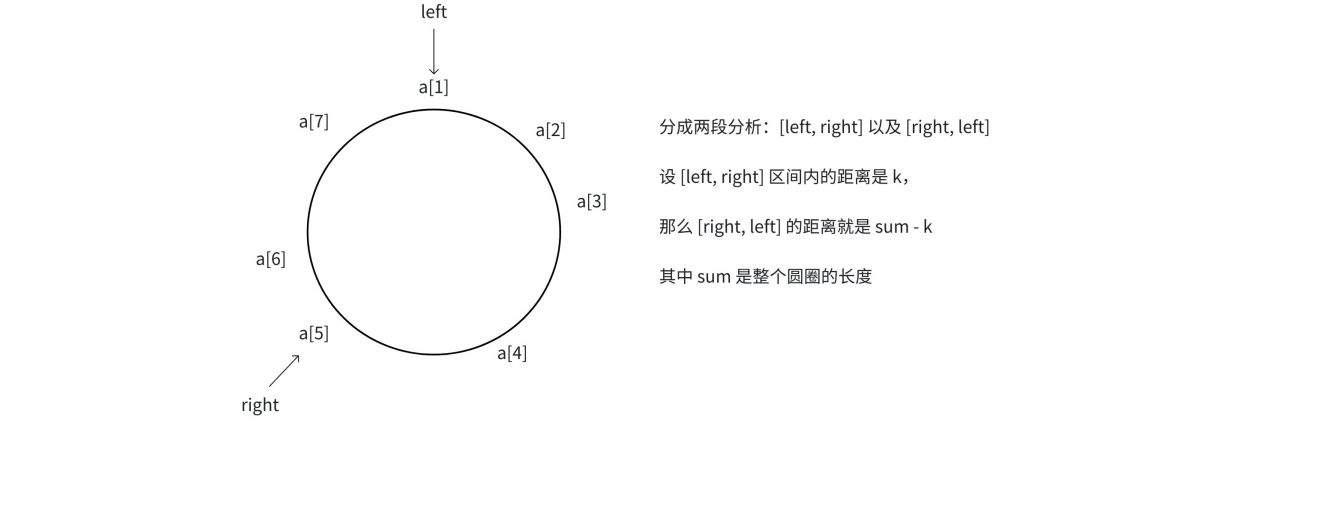
当我们「暴力枚举」的过程中,固定⼀个起点位置left ,然后right之后向后遍历时,记[left,right]之间的距离为k。当right第⼀次扫描到 k × 2 > sum时(以left为起点到的最远距离为right - 1),此时我们会发现:
• right 无需再向后遍历,因为继续向后走的结果⼀定不是最优的;
• left向后移动⼀格之后,right指针也不用回退,因为我们已经维护出来一个合法区间的信息,right回退也不是最优解。
解法 :
(1)进窗口:right 位置与前⼀个位置的距离累加到k 中;
(2)判断:k × 2 > sum 时,此时right 指针不用前进,应该让left 所指的元素出窗口
(3)出窗口:让left 所指位置与前⼀个位置的距离累减到k 中;
(4)更新结果:需要在两个地方更新:
a. 判断结束之后,此时[left, right] 之间可能是最优解,用k更新结果;
b. 判断成立的时候,此时[right, left] 之间可能是最优解,用sum − k 更新结果。
2.4.3 代码
c
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int main()
{
int n;
cin >> n;
int sum = 0;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
sum += a[i];
}
int l = 1, r = 1;
int ret = 0;
int k = 0;
while (r <= n)
{
k += a[r];
while (2 * k > sum) // 用 sum - k 来更新结果
{
ret = max(ret, sum - k);
k -= a[l++];
}
ret = max(ret, k); // 用 k来更新结果
r++;
}
cout << ret << endl;
return 0;
}总结与每日励志
✨本文介绍了双指针算法的原理及其在算法题中的应用。双指针算法通过优化暴力枚举策略,利用两个指针不回退的特性来降低时间复杂度。文章重点讲解了三个经典算法题:唯一的雪花、逛画展和字符串,详细分析了每个问题的解题思路和代码实现。通过滑动窗口技术,可以有效解决涉及子区间统计、字符种类统计等问题。作者还分享了在解题过程中遇到的边界条件处理技巧,帮助读者更好地理解和应用双指针算法。
