论文笔记（一百一十二）Pos3R: 6D Pose Estimation for Unseen Objects Made Easy

Pos3R: 6D Pose Estimation for Unseen Objects Made Easy

文章概括
ABSTRACT
[1. Introduction](#1. Introduction)
[2. Related Work](#2. Related Work)
[3. 6D Pose Estimation with Pos3R](#3. 6D Pose Estimation with Pos3R)
- [3.1. Task Definition](#3.1. Task Definition)
- [3.2. Training-Free Pipeline](#3.2. Training-Free Pipeline)
- - [3.2.1. Template Rendering](#3.2.1. Template Rendering)
  - [3.2.2. Image Matching](#3.2.2. Image Matching)
  - [3.2.3. Pose Fitting](#3.2.3. Pose Fitting)
[4. Experiments](#4. Experiments)
- [4.1. Experimental Setup](#4.1. Experimental Setup)
- [4.2. Comparison With the State of the Art](#4.2. Comparison With the State of the Art)
- [4.3. Component Analysis](#4.3. Component Analysis)
[5. Conclusion](#5. Conclusion)

文章概括

引用：

bash 复制代码

@inproceedings{deng2025pos3r,
  title={Pos3R: 6D Pose Estimation for Unseen Objects Made Easy},
  author={Deng, Weijian and Campbell, Dylan and Sun, Chunyi and Zhang, Jiahao and Kanitkar, Shubham and Shaffer, Matt E and Gould, Stephen},
  booktitle={Proceedings of the Computer Vision and Pattern Recognition Conference},
  pages={16818--16828},
  year={2025}
}

markup 复制代码

Deng, W., Campbell, D., Sun, C., Zhang, J., Kanitkar, S., Shaffer, M.E. and Gould, S., 2025. Pos3R: 6D Pose Estimation for Unseen Objects Made Easy. In Proceedings of the Computer Vision and Pattern Recognition Conference (pp. 16818-16828).

主页：
原文：
代码、数据和视频：

系列文章：

请在《《《文章》》》专栏中查找

宇宙声明！

引用解析部分属于自我理解补充，如有错误可以评论讨论然后改正！

ABSTRACT

基础模型显著降低了对任务特定训练的需求，同时也提升了泛化能力。然而，最先进的6D位姿估计方法要么仍需要在位姿监督下进一步训练，要么忽视了从3D基础模型中可以获得的进展与收益。后者是一种错失良机，因为这类模型更擅长预测与三维一致的特征，而这对位姿估计任务具有重要价值。为弥补这一空白，我们提出Pos3R：一种从单张RGB图像估计任意物体6D位姿的方法，它大量利用3D重建基础模型，并且不需要任何额外训练。我们指出模板选择是现有方法的一个关键瓶颈；借助3D模型可以显著缓解这一问题，因为相较于2D模型，3D模型更容易区分不同的模板位姿。尽管方法很简单，Pos3R在6D物体位姿估计基准（BOP）上仍取得了有竞争力的表现，可与现有无需refinement（精化/细化）的方案相当，甚至超过它们。此外，Pos3R还能与"渲染-对比"（render-and-compare）的位姿精化技术无缝结合，显示出面向高精度应用的适应性。

1. Introduction

六维（6D）物体位姿估计------即确定物体相对于相机的精确位置和朝向的任务------在机器人、增强现实以及自主系统等应用中至关重要。可靠的位姿估计能够支持诸如物体操作、抓取和装配等关键任务，使这些系统能够在复杂且动态的环境中实现有效交互 [6, 18, 29, 30, 49, 54]。传统方法通常依赖于针对特定物体或类别定制的学习型模型，虽然能够取得较高精度，但在泛化到新类别或未见过的物体时往往表现不佳 [4, 5, 7, 26, 33, 46, 47, 53--55, 59, 61]。在动态变化且数据稀缺的环境中，这种局限性尤为突出，而在此类场景下，系统的适应性与灵活性至关重要。

6D位姿估计要输出两样东西：

位置（translation，3个自由度）：物体中心在相机坐标系里在哪里（x,y,z）

朝向（rotation，3个自由度）：物体怎么转的（绕x/y/z轴转多少）

合在一起就是一个刚体变换 T c ← o = [ R ∣ t ] T_{c\leftarrow o} = [R|t] Tc←o=[R∣t]（你可以把它理解成：把物体坐标系"搬"到相机坐标系的那把尺子和方向盘）。为什么难？因为相机看到的是2D图像，你要从2D恢复3D的"位置+方向"，这是典型的"信息不够"问题，所以必须借助：

几何约束（PnP）

多视角/模板（render-and-compare）

强特征（foundation models）
1. 传统方法为什么不够用？（原文第一段要表达的核心）

传统学习法通常是：

给一堆训练数据 → 训练一个专门识别某些物体/某些类别的网络 → 在这些物体上很准

但如果来了没见过的新物体 （unseen object），它就容易崩。这就是文章说的"泛化到新类别或未见物体表现不佳"。

在机器人真实场景里，物体千奇百怪、数据又少，所以才需要"更通用"的方法。

为克服上述限制，近年来研究逐渐转向基于模型的方法，旨在无需针对具体物体训练的情况下，将位姿估计泛化到未见过的物体 [2, 17, 41, 56]。这类方法通常采用两阶段流程：首先在场景中检测并定位物体，其次通过"渲染-对比"（render-and-compare）过程，将检测到的物体区域与一组模板模型进行匹配。在这一思路基础上，近期研究通过大规模模型训练并重点关注物体多样性，以进一步提升泛化能力。例如，FoundationPose [56] 结合合成训练数据、大语言模型以及对比学习，从而增强跨不同领域的特征对齐能力，实现更稳健的泛化。

2. 基于模型（model-based）两阶段方法在做什么？

原文说很多方法转向"基于模型"的两阶段流程，大概是这样：

Stage A：检测+定位（找到物体在哪）

先在图像里找出物体区域（bbox/mask），至少知道"物体大概在这块"。

Stage B：渲染-对比（render-and-compare）

你有物体的 CAD 模型（3D几何），你可以在电脑里"假装有一台相机"从不同角度把它渲染成很多模板图。

然后把真实图里的物体区域和这些模板图去比，找一个最像的模板角度，从而推出物体的位姿。

卡点解释：

你可以把模板想成"这物体如果以某个角度摆着，相机会看到什么样子"。

真实图像 = 不知道角度的答案图

模板库 = 候选答案

匹配 = 选最像的答案

FoundationPose 这类方法做得更强，是因为它用更大规模训练去学更"对得上"的特征（跨域对齐更好）。

近年来无训练（training-free）方法的出现提供了一种有前景的替代方案，使得在无需针对物体或任务进行专门训练的情况下即可对未见物体进行6D位姿估计。诸如 DINOv2 [40] 等基础模型已展现出强大的零样本能力，能够通过学习到的特征同时捕获空间和语义细节 [1, 58]。例如，FoundPose [41] 利用 DINOv2 的特征描述子来弥合合成数据与真实数据之间的差距，并在 BOP 挑战赛中取得了具有竞争力的结果 [17]。这些进展凸显了无训练框架在6D位姿估计领域的巨大潜力。

3. training-free（无训练）为什么会成为趋势？

因为它很诱人：

不针对物体训练也能做未见物体位姿估计

做法核心是：用一个"强大的通用特征提取器"（foundation model）来做匹配。 DINOv2 就是这样的 2D 基础模型：它能从图像里提取很强的局部+语义特征，所以拿来做"模板图 ↔ 真实图"的匹配，看起来很合理。 FoundPose 就是把 DINOv2 的特征用于合成到真实的匹配，取得了不错成绩。但------文章的关键转折点来了：仅靠 2D 特征，在"平面外旋转"上会出问题。

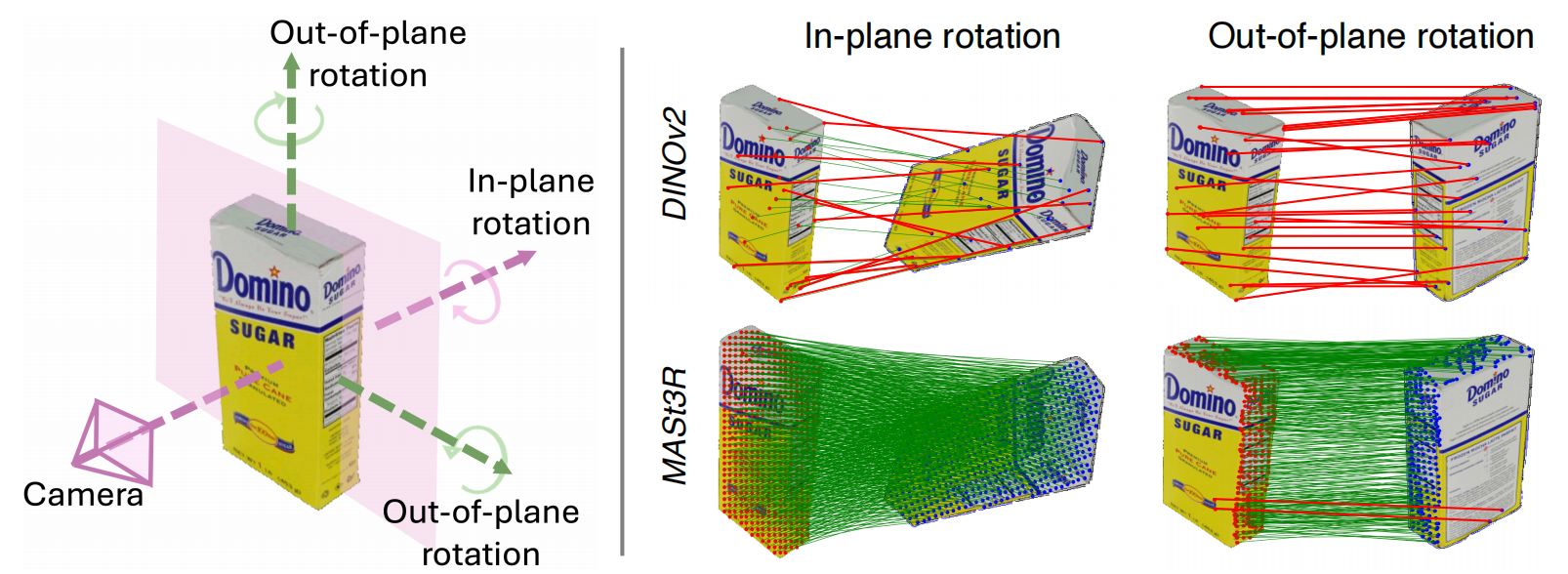图1：平面内旋转与平面外旋转示意，以及DINOv2与MASt3R在对应关系质量上的对比。左侧示意图从相机视角展示了平面内旋转（发生在图像平面内）与平面外旋转（三维朝向变化）。右侧对DINOv2 [40]（上排）与MASt3R [24]（下排）在处理这些旋转时的表现进行了对比。由于其2D特征的局限性，DINOv2呈现出稀疏且不一致的对应关系（用红线表示），尤其在平面外旋转情况下更为明显。相比之下，MASt3R在两类旋转下都能提供稠密且稳定的对应关系，这体现了它生成三维一致特征的能力。

在这一趋势的基础上，我们进一步探索3D基础模型的优势。精确的位姿估计需要同时处理平面内旋转和平面外旋转，如图1所示。平面内旋转发生在图像平面内，例如物体绕相机视线方向旋转；而平面外旋转则涉及三维朝向的变化，如倾斜或转动，由于视角变化会显著改变物体外观。由于物体常常以不同视角出现，同时处理这两类旋转对于实现鲁棒的位姿估计至关重要。尽管像 DINOv2 这样的2D基础模型可以通过数据增强较好地处理平面内旋转，但由于其二维特性的限制，在应对平面外旋转时缺乏足够的鲁棒性（如图1所示）。相比之下，诸如 MASt3R [24] 的3D基础模型专门设计用于在不同视角下生成三维一致的特征，即使在平面外旋转情况下也能实现可靠的特征对齐。

4. 图1到底想告诉你什么？（这是整段动机的"灵魂"）

图1把旋转分成两类：

4.1 平面内旋转（In-plane rotation）

物体在图像平面里转，比如像一张照片在桌面上旋转：

外观变化相对"简单"

2D特征通过数据增强通常还能扛得住

4.2 平面外旋转（Out-of-plane rotation）

物体真的在3D里倾斜、侧转，比如你把盒子从正面转到侧面：

你看到的面变了

遮挡关系变了

纹理/边缘投影都变了

外观变化非常大

这就是6D位姿估计最难的部分之一：同一个物体换个视角，图像差别巨大。

5. 为什么 DINOv2 在平面外旋转下匹配差？（原文给的解释是"2D特征限制"）

你看图1右上（DINOv2）：

平面内旋转：还能连出一些对应（红线稀疏但还凑合）

平面外旋转：对应变得更稀疏、更乱、更不一致

直觉解释（不改变原意，用老师的说法）：

DINOv2 的特征主要是"看图像像不像"，它并不保证"同一个3D点在不同视角下还能被稳定认出来"。

平面外旋转时，同一个3D点在图像上会发生大变化：

位置大移动

外观可能从"亮面"变"暗面"

甚至直接不可见（被遮挡）

2D特征就容易"认错人"或"找不到人"。

6. MASt3R 为什么能稳？（原文核心：3D-consistent features）

图1右下（MASt3R）你会看到：

不管平面内还是平面外旋转，都能产生稠密、稳定的对应（大量绿线，整体很一致）

这意味着什么？意味着：

MASt3R 提取的不是"随便的2D相似性特征"，而是更接近"同一个3D表面点在不同视角下仍可对齐"的特征。

你可以把它理解成：

DINOv2 更像"图像理解的通用特征"

MASt3R 更像"为多视角/3D一致性设计过的特征"

所以文章说：MASt3R 反映了其生成 3D一致特征 的能力。

受此启发，我们提出 Pos3R，一种仅使用 RGB 输入、无需训练的未见物体6D位姿估计方法。 Pos3R 利用3D基础模型 MASt3R [24] 进行位姿估计，而无需任何额外训练。 Pos3R 的核心在于测试图像裁剪区域与由 CAD 模型渲染得到的模板图像之间的匹配过程。由于存在域差异，诸如 LoFTR [50] 等常见匹配器在合成数据到真实数据的匹配中往往表现不佳，而 MASt3R 在该场景下能够生成高质量的二维对应关系。这些可靠的匹配使 Pos3R 能够构建位姿估计所需的2D-3D对应关系，并利用 PnP-RANSAC 算法完成位姿求解。

7. Pos3R：整篇方法在"怎么做"？（按输入→模块→输出讲清楚）

Pos3R 的定位是：

只用 RGB

training-free（不额外训练）

未见物体 6D 位姿估计

用 MASt3R 来做跨域匹配（真实 vs CAD渲染）

7.1 输入是什么？

一张真实RGB图像

物体的 CAD 模型（你可以渲染它）

图像中物体的裁剪区域（通常来自检测器）

7.2 核心流程是什么？

可以概括为 4 步（这就是它的"算法结构"）：

Step 1：为 CAD 物体生成少量但"覆盖充分"的模板（Template Rendering）

传统方法可能渲染几百上千张模板，因为怕漏角度。

Pos3R 的关键省计算点是：只渲染 40 张/物体，但覆盖两类旋转：

(1) 覆盖平面外旋转：8 个基础模板

怎么来的？把相机放在"以物体为中心的立方体 8 个顶点"位置去看物体。这样等价于从 8 个"非常分散"的方向观察，能覆盖主要的 3D朝向变化（out-of-plane）。你可以把它想成：从"东北上""西南下"等8个角度看盒子。
(2) 覆盖平面内旋转：每个基础模板再转 5 次

在每个基础视角下，再绕相机视线方向转几下（in-plane rotation），得到 5 张。所以总数 = 8 × 5 = 40 8 \times 5 = 40 8×5=40。 卡点解释：为什么这样就够？ 因为 out-of-plane 是"换面"的大变化，先用 8 个方向把"换面"覆盖住； in-plane 是"同一面上旋转"的小变化，再用 5 个角度补齐就行。这就是文章说的"合理放置相机位置来覆盖平面内与平面外旋转"。

Step 2：用 MASt3R 做"真实裁剪图 ↔ 模板图"的高质量对应（Dense Correspondence）

对每一个模板图，MASt3R 会输出很多对齐关系：

真实图上的点 ↔ 模板图上的点
而且是稠密、稳定的（这是图1证明的关键能力）。

这里文章特别强调了一点：

由于域差异，LoFTR 这类常见匹配器在合成→真实往往不行，但 MASt3R 可以。

卡点解释：域差异是什么？

CAD渲染图通常：纹理干净、光照理想、背景简单

真实图：噪声、反光、阴影、模糊、背景复杂

很多匹配器会被这种差别骗到。MASt3R更扛这种跨域差异。

Step 3：把 2D-2D 匹配"升级"为 2D-3D 对应（为了能解位姿）

PnP 要的不是"图对图"，而是：

图像中的 2D 点（在真实图上）

对应物体模型上的 3D 点（在CAD上）

那 Pos3R 怎么拿到 3D 点？关键在于：模板图是你渲染出来的。渲染时你知道：

模板图上的每个像素，来自 CAD 上哪个 3D 点（通过渲染的深度/投影信息可得）

所以流程是：

真实图 2D点 ↔（MASt3R）↔ 模板图 2D点 ↔（渲染记录）↔ CAD 3D点

这样就构建出了大量 2D-3D 对应。

Step 4：PnP-RANSAC 求解 6D 位姿（最终输出）

有了很多 2D-3D 对应点，就能用经典几何求解：

PnP（Perspective-n-Point） ：求 R , t R,t R,t 使得 3D 点投影到图像后尽量对上 2D 点

RANSAC：因为匹配里总会有错的点（outliers），RANSAC 会不断随机抽样、找"最一致"的那一批点，从而抗错误匹配

卡点解释：为什么一定要 RANSAC？ 匹配再强也会有错点。 PnP 如果吃进大量错点，会直接算出离谱姿态。 RANSAC 的作用就是：让少量错点不会毁掉整体解。

通过利用 MASt3R 在视角和光照变化下仍能生成稠密对应关系的能力，我们简化了模板生成过程并提升了计算效率。不同于需要渲染数百个模板的现有方法，我们通过合理放置相机位置来覆盖平面内与平面外旋转。具体而言，我们为每个物体使用八个基础模板，将相机放置在以 CAD 模型为中心的立方体顶点处，以覆盖平面外旋转。针对每个基础模板，我们沿物体主轴生成五个平面内旋转模板，从而每个物体共得到四十个模板。为确保高效且准确的位姿估计，Pos3R 会根据匹配质量动态选择最优旋转。这一简单而有效的策略在保持计算效率的同时，实现了可靠的位姿估计。在 BOP 挑战赛的七个多样化数据集上进行测试后，Pos3R 展现出强劲性能，成为一种鲁棒、可扩展的无训练未见物体6D位姿估计方案，并且可适配渲染-对比式精化技术。

8. "根据匹配质量动态选择最优旋转"是什么意思？（很多人会卡这里）

你现在有 40 个模板，每个模板都能跑一遍匹配 + PnP。那选哪个？

Pos3R 的策略很朴素也很有效：

对每个模板：算一套位姿 + 一个"匹配质量分数"（例如内点数量、重投影误差、匹配一致性等）

选分数最高的模板对应的位姿作为最终结果（或进入后续精化）

这就是文章说的：

根据匹配质量动态选择最优旋转

简单但有效，兼顾效率与准确性

综上所述，我们的主要贡献包括：

针对现有方法主要依赖2D基础模型进行未见物体位姿估计的问题，我们提出了 Pos3R，这是一种利用3D基础模型 MASt3R [24]、无需训练且更具鲁棒性的方法。
借助 MASt3R 稳定的稠密对应关系，Pos3R 每个物体仅使用40个精心布置的模板即可覆盖平面内与平面外旋转，并通过基于对应质量的简单选择策略实现准确匹配，在 BOP 挑战赛中取得了优异表现。

Seen Object Pose Estimation（已见物体位姿估计）已见物体位姿估计。实例级物体位姿估计是指对模型训练阶段已经见过的特定物体进行位姿估计的任务 [5, 7, 26, 33, 46, 54, 61]。常见方法之一是基于对应关系的方法，该类方法学习在输入数据与物体的 CAD 模型之间建立精确对齐关系 [7, 27, 46]。另一类方法采用基于模板的策略，即从预定义的带有位姿标注的模板集合中选择与当前输入最相似的模板 [25, 35, 52]。此外，基于回归的方法直接从学习到的物体特定特征中预测物体位姿 [12, 19, 26, 42]。

这些实例特定的方法虽然精度较高，但通常需要针对新物体实例重新训练，从而限制了其泛化能力。这一局限促使研究者探索类别级方法，该类方法在特定物体类别内部进行泛化，使得能够对已知类别中的未见物体进行位姿估计 [4, 47, 53, 55, 59]。例如，SecondPose [4] 通过将物体特定的几何特征与 DINOv2 的 SE(3) 一致语义先验相结合，提升了类别级 6D 位姿估计效果，有效缓解了类别内形状差异的问题。然而，这类方法在目标类别之外往往表现不佳，而我们的方法不依赖此类类别约束，从而支持更广泛的应用场景。

Unseen Object Pose Estimation（未见物体位姿估计）未见物体位姿估计。为提升位姿估计的灵活性，许多方法致力于在无需针对特定物体训练的情况下泛化到新的物体实例 [22, 31, 37, 39, 43]。针对该任务的方法大致可分为基于人工参考视图的方法和基于 CAD 模型的方法。（i）基于参考视图的方法使用具有已知位姿的多视角图像作为位姿估计的参考数据 [14, 31, 43, 51]。例如，OnePose [14, 51] 从带位姿标注的 RGB 图像中重建物体的三维点云，并通过建立 2D--3D 对应关系来求解 6D 位姿。另一种方法 Nope [38] 从生成新视角的角度出发，训练模型预测对新物体视角具有判别力的嵌入表示。（ii）基于 CAD 模型的方法利用三维物体模型来辅助位姿估计。部分方法在 CAD 模型与查询图像之间进行特征匹配 [20, 28, 60]，而另一些方法则通过模板匹配寻找最接近的初始位姿，并借助专门的精化模块进一步提升精度 [22, 34, 39]。例如，GigaPose [39] 提出了一种高效的双网络系统：一个网络用于检索模板视图（平面外旋转），另一个网络用于估计剩余自由度（平面内旋转与三维平移）。这种分离设计降低了计算开销，相比之下，MegaPose [22] 对每一个可能的测试裁剪与模板对都使用同一个网络进行处理。我们的工作基于 CAD 模型的方法，并与近期 BOP 挑战赛的评测协议保持一致 [17]。我们专注于一种无需训练的未见物体位姿估计流程，这一方向不同于需要大量任务特定网络训练的方法。

Training-Free Object Pose Estimation（无训练位姿估计）无训练物体位姿估计。传统上，6D 物体位姿估计通常通过建立 3D--2D 对应关系，然后使用 PnP 算法完成求解 [11, 13, 44, 61]。近年来，利用基础模型特征进行位姿估计逐渐受到关注，尤其是 DINO 等模型，它们为位姿估计提供了丰富的空间细节和语义一致性 [1, 58]。 FoundPose [41] 使用 DINOv2 描述子来弥合合成数据与真实数据之间的域差异，在仅使用 RGB 输入的情况下，对对称物体取得了较强性能。 FreeZe 将来自 GeDi [45] 的三维点描述子与来自 DINOv2 [40] 的图像特征相结合，用于 RGB-D 位姿估计。通过利用 MASt3R 的三维一致特征生成稠密对应关系，我们的工作探索了一种仅使用 RGB 输入、无需训练的未见物体位姿估计方法，从而在无需任务特定训练的情况下实现对多样物体类别的有效位姿估计。

3. 6D Pose Estimation with Pos3R

3.1. Task Definition

1）这段话在干嘛？一句话说清楚

它在定义一个任务：

你给我 一个物体的3D模型 和 一张包含这个物体的RGB照片 ，并且我知道相机的参数。

我要算出：这个物体在相机面前到底摆在哪里、朝向怎么转（也就是 6D 位姿）。

这就是 6D pose estimation 的标准定义。

给定一个查询物体的三维模型 Q \mathbf{Q} Q，以及一张包含该物体的 RGB 图像 I ∈ R H × W × 3 \mathbf{I} \in \mathbb{R}^{H \times W \times 3} I∈RH×W×3，在相机内参 K \mathbf{K} K 已知的情况下，任务是估计物体 Q \mathbf{Q} Q 相对于相机参考坐标系的 6D 位姿。具体而言，我们的目标是求解三维空间中的六自由度变换 T = ( R , t ) \mathbf{T} = (\mathbf{R}, \mathbf{t}) T=(R,t)，其中 R ∈ R 3 × 3 \mathbf{R} \in \mathbb{R}^{3 \times 3} R∈R3×3 表示旋转矩阵， t ∈ R 3 \mathbf{t} \in \mathbb{R}^{3} t∈R3 表示平移向量。分割后的物体区域 I m = M ⊙ I \mathbf{I}_m = \mathbf{M} \odot \mathbf{I} Im=M⊙I 通过对二值分割掩码 M \mathbf{M} M 与图像 I \mathbf{I} I 进行逐元素相乘得到，从而仅保留物体 Q \mathbf{Q} Q 的可见部分。需要注意的是，物体 Q \mathbf{Q} Q 可能存在部分遮挡。

2）输入是什么？（你给算法的东西）

这里有三个关键输入：

(A) 查询物体的三维模型 Q \mathbf{Q} Q

Q \mathbf{Q} Q 不是图片，是 3D CAD 模型（网格/点云都行，本质是"它的三维形状"）。

为什么叫"查询物体"？因为它可能是没见过的新物体（unseen object），不靠训练记住它，而是靠这个3D模型来认它、对齐它。

你可以把 Q \mathbf{Q} Q 理解为：

"物体的标准答案几何结构（3D）"。

(B) 一张 RGB 图像 I ∈ R H × W × 3 \mathbf{I} \in \mathbb{R}^{H \times W \times 3} I∈RH×W×3

I \mathbf{I} I 是相机拍的彩色照片。

H × W H \times W H×W 是图片高度和宽度，最后的 3 3 3 表示 RGB 三个颜色通道。

你可以把 I \mathbf{I} I 理解为：

"现实世界里拍到的这个物体的样子（2D）"。

(C) 相机内参 K \mathbf{K} K（已知）

这玩意是很多人最容易卡的点，我直接讲清楚：

相机内参 K \mathbf{K} K 是一个 3 × 3 3\times 3 3×3 矩阵，一般长这样：

K = [ f x 0 c x 0 f y c y 0 0 1 ] \mathbf{K}= \begin{bmatrix} f_x & 0 & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{bmatrix} K= fx000fy0cxcy1

它包含：

f x , f y f_x,f_y fx,fy：相机焦距（像素单位）

c x , c y c_x,c_y cx,cy：主点（图像中心偏移）

它的作用只有一个 ：把 3D 点投影到 2D 图像上。也就是说，如果你猜了一个位姿 ( R , t ) (\mathbf{R},\mathbf{t}) (R,t)，就能算出：

CAD 模型上的 3D 点，在这张图里应该落到哪个像素位置。

后面用 PnP 时，这个 K \mathbf{K} K 是必须的。

3）输出是什么？（你要算法算出来的东西）

输出是物体相对相机的刚体变换：

T = ( R , t ) \mathbf{T}=(\mathbf{R},\mathbf{t}) T=(R,t)

(A) 旋转 R ∈ R 3 × 3 \mathbf{R}\in\mathbb{R}^{3\times 3} R∈R3×3

代表物体"朝向怎么转"

例如盒子正面朝相机、还是侧面朝相机、还是斜着

你可以把 R \mathbf{R} R 想成：

"给物体装一个方向盘，告诉你它转到了哪个角度"。

(B) 平移 t ∈ R 3 \mathbf{t}\in\mathbb{R}^{3} t∈R3

代表物体"在相机前面的位置"

三个数就是 x , y , z x,y,z x,y,z（在相机坐标系里）

你可以把 t \mathbf{t} t 想成：

"物体中心离相机多远、在左边还是右边、在上面还是下面"。

4）为什么要做分割？ I m = M ⊙ I \mathbf{I}_m=\mathbf{M}\odot \mathbf{I} Im=M⊙I 到底是什么意思？

这句也是常见卡点，我用最直白方式解释：

(A) M \mathbf{M} M 是二值分割掩码（mask）

M \mathbf{M} M 和图像一样大 H × W H\times W H×W

每个像素只有两种值：

1：这是物体

0：这不是物体（背景、桌子、手、其它物体）

(B) ⊙ \odot ⊙ 是"逐像素相乘"

如果某个像素在 mask 里是 0，那么：

0 × 0\times 0×（原图像素）= 0
→ 这个像素直接黑掉（等于抹掉背景）

如果 mask 是 1：

1 × 1\times 1×（原图像素）= 原样保留

所以：

I m = M ⊙ I \mathbf{I}_m=\mathbf{M}\odot \mathbf{I} Im=M⊙I

就是把图像变成"只剩下物体那块，其它都被清空"的版本。

(C) 这样做的目的是什么？

为了让后续的"匹配/对应关系"更干净：

不分割的话，匹配器可能把背景纹理（桌面花纹）当成物体特征去匹配，产生大量错对应。

分割后，算法专心看物体表面，成功率更高。

5）"物体可能部分遮挡"这句话为什么要强调？

因为遮挡会让两个事情变难：

图像里可见的物体表面变少

对应关系会变稀疏/更容易错

但这段定义里强调它，是在告诉你：

我们的输入条件允许遮挡（不是理想情况），方法需要在这种情况下仍能工作。

注意：这里还没讲"怎么解决遮挡"，只是把问题设定说清楚------后面章节会用 MASt3R 的稠密对应与鲁棒匹配来支撑。

本文利用 3D 基础模型 MASt3R [24] 来解决基于模型的未见物体 6D 位姿估计问题。我们提出 Pos3R，这是一种无需训练、仅使用 RGB 输入的方法，能够在不依赖物体或任务特定训练的情况下有效估计 6D 位姿。

6）这里的"基于模型（model-based）未见物体 6D 位姿估计"到底是什么意思？

这是整篇文章的定位词，你要把它读懂：

未见物体（unseen object）：训练阶段没见过它（甚至不训练）

基于模型（model-based） ：不是靠记忆，而是靠 3D CAD 模型 Q \mathbf{Q} Q 来推位姿

6D 位姿估计 ：输出 ( R , t ) (\mathbf{R},\mathbf{t}) (R,t)

一句话：

"我不用训练记住这个物体，我直接用它的3D CAD模型来和图片对齐，从而算出它摆放的姿态。"

7）MASt3R 在这里扮演什么角色？（模型位置讲清楚）

这段最后说：

本文利用 3D 基础模型 MASt3R 来解决这个问题，并提出 Pos3R。

你可以把 MASt3R 的角色理解为：

MASt3R = "超级强的跨视角匹配器/对应关系生成器"

它最核心的能力（和前面图1一致）是：

给两张图（真实裁剪 vs CAD渲染模板），它能找到很多"这儿对应那儿"的匹配点

并且这种对应对 平面外旋转（视角变化大） 更稳

而 Pos3R 就是：

Pos3R = "把 MASt3R 的对应关系，变成 6D 位姿的完整流水线"

你现在这段只在定义任务，所以还没展开流水线；但后面一定会走向：

渲染模板图（来自 CAD）

用 MASt3R 在模板图和真实图之间找对应

把 2D 对应变成 2D-3D 对应

用 PnP-RANSAC 求 ( R , t ) (\mathbf{R},\mathbf{t}) (R,t)

8）"无需训练、仅使用 RGB 输入"到底意味着什么？

这也是定位语，必须读准：

无需训练（training-free）：作者不再额外训练一个网络来适配数据集/物体 → 直接拿 MASt3R 作为现成的基础模型用

仅使用 RGB：不用深度相机、不用多视角、不用IMU，不需要额外传感器 → 输入只有一张彩色图（加上 CAD 模型）

所以它强调的是：方法部署成本低、泛化潜力强（因为不依赖特定训练）。

9）把这段"任务定义"用一张脑内图串起来（最容易记）

你有：

CAD 模型 Q \mathbf{Q} Q（3D）

RGB 图 I \mathbf{I} I（2D）

相机内参 K \mathbf{K} K（投影规则）

分割 mask M \mathbf{M} M（只看物体）

你要求：

位姿 T = ( R , t ) \mathbf{T}=(\mathbf{R},\mathbf{t}) T=(R,t)

这就是这段话的全部内容：把问题说得可计算、可复现、无歧义。

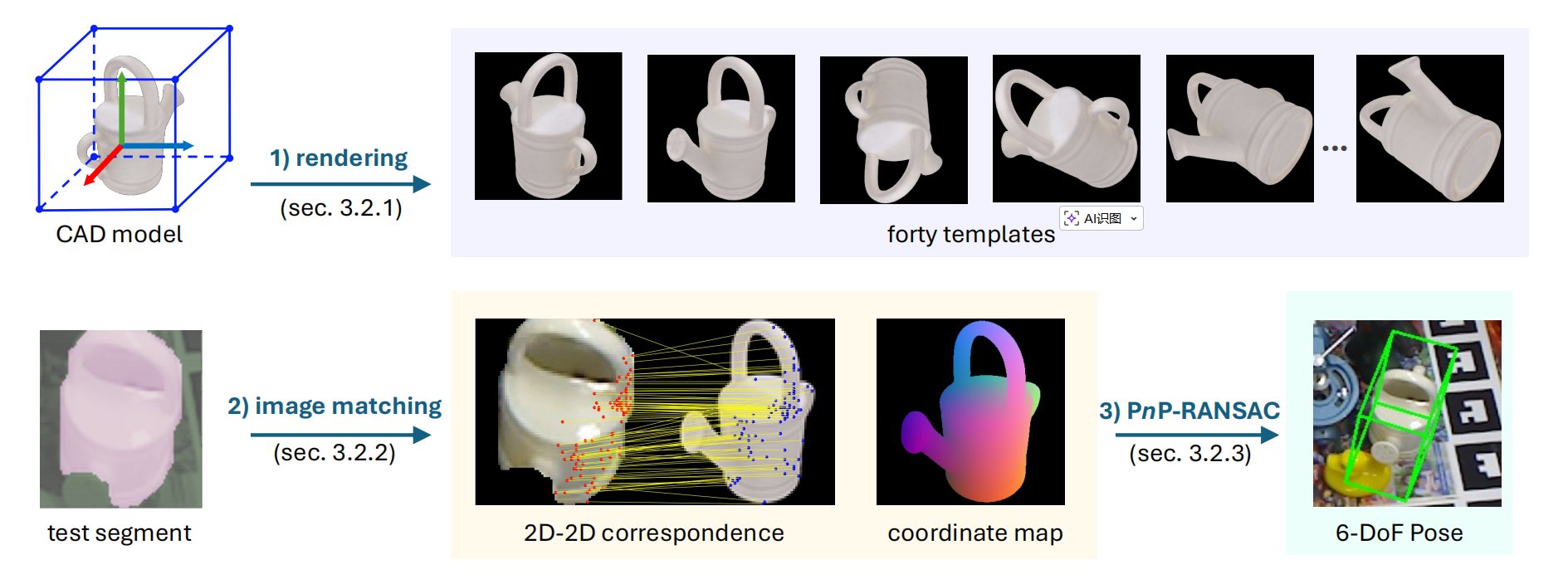图2：Pos3R 中 6D 位姿估计流程概览。（1）模板渲染（第 3.2.1 节）：使用 CAD 模型生成四十个模板，每个模板表示一种独特的朝向，覆盖平面内与平面外旋转。这一过程通过将相机放置在围绕物体的立方体顶点处来实现。（2）图像匹配（第 3.2.2 节）：给定来自 CNOS [37] 的测试图像分割区域，我们在测试图像与每个渲染模板之间建立 2D--2D 对应关系。我们利用 MASt3R [24] 生成的三维一致特征进行精确匹配，并根据匹配质量选择最佳模板。每个模板还包含一张三维物体坐标映射，用于记录对应的三维点。（3）位姿拟合（第 3.2.3 节）：利用选定的对应关系，我们应用 PnP-RANSAC 算法 [23] 得到最终位姿，使物体与其在场景中的观测位置对齐。

3.2. Training-Free Pipeline

概述遵循未见物体 6D 位姿估计的标准基于模型流程 [2, 39, 41]，Pos3R 由两个组件构成：目标检测与位姿估计。我们将各组件保持冻结（参数不更新），避免任何针对特定物体或特定任务的训练。

1）先把大框架抓住：Pos3R 是一个"两段式流水线"

这段话说 Pos3R 遵循未见物体 6D 位姿估计的标准"基于模型（model-based）"流程，它由两个组件构成：

目标检测（更准确说：检测 + 分割 + 识别）

位姿估计（Pose Estimation）

你可以把它想成：

第一步：先在图里把"物体从背景里抠出来"，并且知道它是谁。

第二步：再把"抠出来的物体"跟 CAD 模型对齐，算出它的 6D 位姿。

这就是"标准流程"的含义：很多 BOP 体系的 unseen object pose 方法都这么分两段做。

2）什么叫 Training-Free？"冻结组件"到底是什么意思？

这段话强调：我们将各组件保持冻结（参数不更新），避免任何针对特定物体或任务的训练。

这里有两个非常关键的点：

(A) Training-free ≠ 系统里完全没用到训练过的模型

它用的 CNOS、MASt3R 都是别人训练好的模型。 "Training-free"的意思是：

你在这个任务上不再做任何额外训练/微调（不会为了你的物体、你的场景再训练一次）。

(B) 冻结（frozen）是什么意思？

就是"只推理，不学习"：

推理时：输入进去 → 输出结果

不会反向传播、不更新参数、不改权重

好处是：

对 unseen object 更公平（不靠针对物体训练）

部署简单（不需要收集新数据再训练）

在目标检测部分 ，我们使用 CNOS [37] 为每个目标实例生成分割掩码与物体身份标识，从而在 RGB 图像 I \mathbf{I} I 中定位目标分割区域 I m \mathbf{I}_m Im。作为 BOP 挑战赛中用于未见物体分割的默认方法，CNOS 仅需要 3D 模型即可完成接入（onboarding），并不依赖额外数据或针对物体的专门训练。

3）第一部分：目标检测/分割模块在做什么？（CNOS 的角色）

这段说：

使用 CNOS 为每个目标实例生成 分割掩码 与 物体身份标识 ，从而在 RGB 图像 I \mathbf{I} I 中定位目标分割区域 I m \mathbf{I}_m Im。

我把它拆开讲：

3.1 CNOS 输出两样东西

(1) 分割掩码 mask

你已经见过 M \mathbf{M} M，它是 H × W H\times W H×W 的 0/1 图：

1：物体像素

0：背景像素

有了它，就能得到"只剩物体"的图：

I m = M ⊙ I \mathbf{I}_m=\mathbf{M}\odot \mathbf{I} Im=M⊙I

这一步非常重要，因为后面的位姿估计需要在物体表面找对应点；如果背景没去掉，匹配会被背景干扰。

(2) 物体身份标识（object ID）

BOP 里经常不是一张图只有一个物体，可能有多个物体实例。 CNOS 不仅告诉你"这里有一个物体"，还告诉你"它对应哪个 CAD 模型"。你可以把它理解成：

"抠出来之后，还要知道你抠的是 A 模型还是 B 模型，否则后面不知道用哪个 CAD 去渲染模板。"

3.2 为什么 CNOS 适合 "未见物体分割"？

原文强调：CNOS 是 BOP 的默认 unseen object segmentation 方法，并且：

仅需要 3D 模型即可 onboarding（接入），不依赖额外数据或针对物体训练

这句话用大白话解释是：

你给它一个物体的 CAD 模型

它就能开始在图片里找这个物体、抠出 mask

不用你再为这个物体拍一堆图来训练一个分割网络

这正符合"未见物体 / training-free"设定：来了新物体也能用。

在 6D 位姿估计部分 ，我们在图2中展示了三个步骤。具体而言，给定一组由带纹理的 CAD 模型渲染得到的模板，Pos3R 使用 3D 基础模型 MASt3R [24] 从目标分割区域 I m \mathbf{I}_m Im 以及每个模板中提取特征，并通过建立 2D--3D 对应关系，结合 PnP-RANSAC 算法来估计六自由度变换 T = ( R , t ) \mathbf{T} = (\mathbf{R}, \mathbf{t}) T=(R,t)。

4）第二部分：6D 位姿估计模块在做什么？（MASt3R + PnP-RANSAC）

这段说位姿估计部分有"三个步骤"（图2里画了），并且核心是：

给定一组由 带纹理 CAD 模型渲染的模板

用 MASt3R 从真实的分割区域 I m \mathbf{I}_m Im 和每个模板提特征

建立 2D--3D 对应

用 PnP-RANSAC 解出 ( R , t ) (\mathbf{R},\mathbf{t}) (R,t)

我按"你写代码时会怎么实现"的顺序，把它讲成 3 步。

Step 1：先准备模板（templates）------为什么要渲染"带纹理"的 CAD？

什么是模板？ 模板就是：

"假设物体以某个姿态摆着，相机会看到的渲染图像。"

你渲染很多不同角度的模板，后面就能在这些候选里找到最像真实图的那个角度。

为什么强调"带纹理"？ 因为匹配不是只看轮廓，还要看表面图案/文字/颜色信息。例如盒子上有 "Domino Sugar" 的文字，如果模板也有纹理，MASt3R 更容易稳定对齐这些局部细节。不带纹理（纯几何灰模）往往特征更弱，匹配更难。

Step 2：用 MASt3R 在 "真实裁剪图 ↔ 模板图" 之间找对应关系

这一步是整条链路的"最关键的感知引擎"。

你可以把 MASt3R 当成一个非常强的函数：

输入两张图（真实物体区域、模板渲染图）

输出大量"这个像素对应那个像素"的匹配点（而且对视角变化更稳）

为什么要用 MASt3R？ 因为 Pos3R 的动机就是：2D 基础模型（如 DINOv2）在平面外旋转时对应不稳定；MASt3R 能给出更稠密、稳定的对应。

它说"提取特征"是什么意思？ 不是简单提一个全局向量，而是提一种"每个位置都有描述子"的特征图。这样才能说"图上这个点"对应"另一张图上那个点"。

Step 3：把 2D--2D 对应变成 2D--3D 对应，然后用 PnP-RANSAC 求位姿

4.3.1 为什么一定要 2D--3D 对应？

因为最终要解的是 3D 位姿。几何求解（PnP）要求你提供：

图像上的 2D 点（像素坐标）

模型上的 3D 点（CAD 坐标）

那 3D 点从哪来？答案是：从 CAD 模型 + 渲染过程来。

你渲染模板时，本质上做了"3D→2D投影"。因此模板图上的一个像素点，你可以追溯它来自 CAD 模型表面的哪个 3D

点（靠渲染得到的深度/可见三角面信息）。

于是就形成链条：

真实图 2D点 ↔（MASt3R匹配）↔ 模板图 2D点 ↔（渲染记录反查）↔ CAD 表面 3D点

这就得到了很多 2D--3D 对应。

4.3.2 PnP-RANSAC 到底在干嘛？一句话讲懂

PnP ：找到一个 ( R , t ) (\mathbf{R},\mathbf{t}) (R,t)，使得"把 CAD 的 3D 点用这个位姿投影到图像上"后，尽量贴合真实图的 2D 点。

RANSAC：因为匹配会有错点，RANSAC 用"反复抽样 + 找一致的内点集合"把错点踢掉，让结果稳定。

你可以把它想成：

PnP 是"解方程算姿态"， RANSAC 是"把坏数据扔掉再解"。

最终就输出文章定义的：

T = ( R , t ) \mathbf{T}=(\mathbf{R},\mathbf{t}) T=(R,t)

3.2.1. Template Rendering

使用带纹理的三维 CAD 模型，我们从不同朝向渲染物体的模板。渲染过程遵循文献 [39] 中描述的标准光栅化方法，采用黑色背景和固定光照设置。渲染相机采用与测试相机相同的内参 K \mathbf{K} K，并且渲染得到的模板与测试图像 I \mathbf{I} I 的尺寸一致。在每个模板中，物体始终保持居中。此外，还记录了渲染模板中每个像素在三维 CAD 模型坐标系下对应的三维位置，从而能够建立 2D--3D 对应关系。

1）模板（template）到底是什么？为什么要渲染它？

你现在只有一张真实照片 I \mathbf{I} I，里面有物体。你还知道这个物体的 CAD 模型（3D）。 Pos3R 的想法是：

我把 CAD 模型从不同角度"拍照"（在电脑里渲染出很多假照片），这些假照片就叫模板。然后拿真实照片里抠出来的物体区域，去和这些模板做像素级匹配。匹配得最好、对应关系最稳定的那个模板角度，就告诉我物体真实的姿态接近哪个角度。

所以模板就是：CAD 模型在某个相机姿态下的渲染图像（带纹理、带光照、固定背景）。

2）模板怎么渲染？这里的"标准光栅化"在说什么？

原文说：遵循 [39] 的标准光栅化方法，黑色背景、固定光照。

你不用把"光栅化"想得很玄，它就是图形学里最常见的渲染方式（OpenGL/DirectX 那套思路）：

把 CAD 模型（三角网格）放在 3D 空间里

放一个虚拟相机

把三角形投影到 2D 平面（屏幕像素）

做遮挡判断（前面的三角形挡住后面的）

给每个像素算颜色（纹理 + 光照）

为什么要固定光照 + 黑色背景？ 因为你做的是"模板对比"，越简单越好控制：

黑背景能减少干扰（模板里只有物体，没有乱七八糟背景）

固定光照让模板之间更一致，避免光照变化让匹配变复杂

这不是为了让模板"像真实照片"，而是为了让"模板库内部更干净可控"。

3）一个非常关键的点：渲染相机内参用同一个 K \mathbf{K} K，尺寸一致，物体居中 ------ 为啥这么做？

原文说：

渲染相机采用与测试相机相同的内参 K \mathbf{K} K

模板尺寸与测试图像 I \mathbf{I} I 一致

每个模板里物体始终居中

这些听起来是"工程细节"，其实都是为了后面几步能顺滑：

3.1 为什么内参必须一样？

因为你后面要用 PnP 做几何求解。PnP 的数学假设是： "这些 3D 点通过这个相机模型投影到 2D 图像上"。

如果你渲染模板用的相机内参跟真实相机不同，就会出现这种灾难：

同一个 3D 点，在模板里的投影位置跟真实相机几何不一致

你即使匹配对了，也会引入系统性误差

最终 PnP 会算歪

所以必须用同一个 K \mathbf{K} K，让"模板投影规律"和"真实相机投影规律"一致。

3.2 为什么尺寸一致、物体居中？

这不是说真实图里物体一定居中，而是说模板生成时：

模板上物体位置标准化了（统一在中心）

这样模板之间可比性更强

也方便你把真实图抠出来的物体区域（ I m \mathbf{I}_m Im）和模板做对应，不需要额外处理"模板物体在左边还是右边"的变化

真实图里物体的位置变化，通常已经通过检测/分割裁剪对齐到了一个"以物体为主"的区域，这样两边就更一致。

4）最核心的"隐藏大招"：记录每个像素对应的 3D 位置 ------ 这到底有多重要？

记录渲染模板中每个像素在 CAD 坐标系下对应的三维位置，从而能够建立 2D--3D 对应关系。

这句话非常关键。因为：

MASt3R 能给你的是：真实图像素 ↔ 模板图像素（2D-2D 对应）

但你要算位姿必须用 PnP，而 PnP 需要：真实图像素 ↔ CAD 三维点（2D-3D 对应）

那怎么把 2D-2D 变成 2D-3D？答案就是这里：

4.1 渲染时你其实知道：模板某个像素"来自哪一个 3D 点"

在光栅化渲染里，一个像素最终被哪个三角面覆盖、对应三角面上哪个位置，是能记录下来的（常见做法是输出一个 "position map / xyz map" 或者存下深度+面片信息再反算）。于是你得到：

模板像素 u ′ u' u′ 对应 CAD 上的 3D 点 X \mathbf{X} X

而 MASt3R 给你：

真实像素 u u u ↔ 模板像素 u ′ u' u′

合起来就有：

真实像素 u u u ↔ CAD 3D 点 X \mathbf{X} X

这就是 2D--3D 对应，PnP-RANSAC 就能开工了。你可以把它理解为：

模板不只是"图片"，它还自带一张"像素→3D坐标字典"。

这张字典是 Pos3R 能从匹配走到位姿的桥梁。

Pos3R 的一个关键组成部分是在目标分割区域与模板之间建立像素级对应关系。由于物体经常以多种不同朝向被观测，精确的位姿估计需要同时处理平面内旋转和平面外旋转。平面内旋转发生在图像平面内，例如物体绕相机视线方向旋转。而平面外旋转则涉及三维朝向变化，例如倾斜或转动，由于视角变化会显著改变物体的外观。现有方法通常通过构建庞大的模板库以及专门的模板选择机制来应对这一挑战。例如，MegaPose [22] 使用数百个模板来覆盖广泛的物体姿态，但维护如此庞大的模板库需要额外的专用模板选择网络。

5）为什么一定要强调像素级对应？（不是粗糙对齐）

因为位姿是"毫米级、角度级"的几何量。粗粒度的"像不像"不够，必须有大量精确点对：

对应越稠密、越准确

PnP 的解越稳，RANSAC 内点越多

这也是为什么后面强调 MASt3R 提供稠密对应。

6）接下来讲"最大的难点"：平面内旋转 vs 平面外旋转 ------ 它们到底是什么麻烦？

原文说：物体会以多种朝向被观测，精确位姿估计需要同时处理两类旋转。

6.1 平面内旋转（in-plane）

物体绕相机视线方向旋转（你可以想象照片在纸面上旋转）：

物体还是那一面

只是整体转了个角度

这类变化很多 2D 特征也能应付，但仍会造成一些"看起来都差不多"的歧义（例如对称图案、重复纹理）。

6.2 平面外旋转（out-of-plane）

物体在 3D 空间中倾斜、翻转（你把盒子从正面转到侧面）：

看见的面变了

遮挡关系变了

外观变化巨大

这是最硬的部分。传统方法为了不漏掉这种变化，往往渲染几百张模板覆盖所有可能姿态。

7）为什么很多方法需要"庞大模板库 + 专用模板选择网络"？（MegaPose 的例子）

原文举 MegaPose：

用数百模板覆盖广姿态

但维护这么大模板库会很重：匹配要算很多次

更麻烦的是：为了从几百张里快速挑出最可能的那几张，常常还要训练一个"模板选择网络"

你可以理解为：

模板越多，越不容易漏姿态，但计算越爆炸；所以他们不得不再加一个网络帮忙挑模板------这就又回到"训练/复杂系统"了。

Template Configuration（模板配置） 为降低对大规模模板库的依赖，Pos3R 利用 3D 基础模型 MASt3R，其能够在不同视角下生成三维一致的特征。这使得 Pos3R 能够在无需数百个模板或复杂选择机制的情况下，有效应对平面外旋转。我们使用一组八个基础模板，记为 { I i } i = 1 8 \{\mathbf{I}i\}{i=1}^{8} {Ii}i=18，用于覆盖关键朝向。这些模板对应的相机位置被放置在以 CAD 模型为中心的立方体顶点处，从而有效覆盖平面外旋转。

8）Pos3R 的关键设计：用 MASt3R 的 3D 一致特征，让模板数大幅减少

原文在 "Template Configuration" 里讲的就是这个：

MASt3R 能在不同视角下产生 3D-consistent features（跨视角一致）

所以不需要几百模板也能应对平面外旋转

于是只用 8 个基础模板 覆盖关键朝向

这 8 个怎么放？

相机位置放在以 CAD 为中心的立方体 8 个顶点处。

为什么是立方体 8 顶点？直觉非常简单：

你想从"尽量分散"的方向看物体

立方体顶点恰好给你 8 个分布均匀、方向差异大的视角

能较好覆盖 out-of-plane 的主要变化

所以这一步就是：用很少的"代表性视角"覆盖"翻到哪一面"的变化。

9）但仅有 8 个还不够：平面内旋转会带来歧义，所以每个基础模板再转 T T T 次

原文说：

为解决平面内（轴向）旋转导致的歧义，我们对每个基础模板施加受控旋转变化。

翻成大白话就是：

你从某个视角看盒子（比如正面略偏上）

盒子可能还会绕"镜头朝向"旋转一点点

如果你模板里没有这些旋转版本，匹配可能就会：

对应质量下降

或者错把旋转当成其它变化，影响最终位姿

所以：每个基础模板 I i I_i Ii，再生成 T T T 个"绕相机主轴旋转"的版本。

为进一步解决由平面内（轴向）旋转引起、可能影响对应质量的歧义问题，我们对每个基础模板施加受控的旋转变化。对于每个模板 I i \mathbf{I}_i Ii，我们绕相机主轴生成 T T T 个旋转，每个旋转由角度
θ k = 2 π k T , k = 0 , ... , T − 1 \theta_k=\frac{2\pi k}{T},\quad k=0,\dots,T-1 θk=T2πk,k=0,...,T−1

定义，从而覆盖完整的 36 0 ∘ 360^\circ 360∘ 范围。在实验中，我们设置 T = 5 T=5 T=5 以平衡效率与精度，从而得到一组旋转增强模板 { I i , k } k = 1 5 \{\mathbf{I}{i,k}\}{k=1}^{5} {Ii,k}k=15。接下来，我们将详细讨论模板选择过程。

10）公式 θ k = 2 π k T \theta_k=\frac{2\pi k}{T} θk=T2πk 到底在表达什么？（很多人看到就懵）

它的意思非常朴素：

你要在 36 0 ∘ 360^\circ 360∘（也就是 2 π 2\pi 2π 弧度）里均匀取 T T T 个角度

第 k k k 个角度就是总圆周的 k T \frac{k}{T} Tk

所以：

k = 0 k=0 k=0： 0 ∘ 0^\circ 0∘

k = 1 k=1 k=1： 36 0 ∘ T \frac{360^\circ}{T} T360∘

k = 2 k=2 k=2： 2 ⋅ 36 0 ∘ T \frac{2\cdot 360^\circ}{T} T2⋅360∘

...

k = T − 1 k=T-1 k=T−1： ( T − 1 ) ⋅ 36 0 ∘ T \frac{(T-1)\cdot 360^\circ}{T} T(T−1)⋅360∘

这就是"均匀覆盖一圈"。

11）为什么选 T = 5 T=5 T=5？这不是拍脑袋，是"效率 vs 精度"的折中

原文说：实验里设 T = 5 T=5 T=5 平衡效率与精度。

意味着：

T T T 越大：模板越多，匹配更细致，可能更准

但 T T T 越大：计算越慢（每个模板都要跑一次匹配+PnP）

他们选 5，是说：

够覆盖典型的轴向旋转变化，同时模板总数不至于爆炸。

最终模板总数是：

8 个基础视角（处理 out-of-plane）

每个视角 5 个 in-plane 旋转

总计 8 × 5 = 40 8\times 5=40 8×5=40 张模板

这就回到你前面总结的"40模板策略"。

3.2.2. Image Matching

MASt3R as an Image Matcher（MASt3R 作为图像匹配器） 我们的方法基于 MASt3R [24]，该模型能够在两张输入图像 I a \mathbf{I}_a Ia 与 I b ∈ R H × W × 3 \mathbf{I}_b \in \mathbb{R}^{H \times W \times 3} Ib∈RH×W×3 之间同时执行局部三维重建与像素级匹配。从概念上讲，MASt3R 可视为一个映射函数 f ( I a , I b ) = Dec ( Enc ( I a ) , Enc ( I b ) ) \mathbf{f}(\mathbf{I}_a, \mathbf{I}_b) = \text{Dec}(\text{Enc}(\mathbf{I}_a), \text{Enc}(\mathbf{I}_b)) f(Ia,Ib)=Dec(Enc(Ia),Enc(Ib))，其中编码器 Enc ( I ) → F \text{Enc}(\mathbf{I}) \rightarrow \mathbf{F} Enc(I)→F 是一个孪生结构的视觉 Transformer（ViT），将图像 I \mathbf{I} I 处理为大小为 N × d N \times d N×d 的 token 向量，其中 N = w × h N = w \times h N=w×h，最终得到 F ∈ R N × d \mathbf{F} \in \mathbb{R}^{N \times d} F∈RN×d。解码器 Dec ( F a , F b ) \text{Dec}(\mathbf{F}_a, \mathbf{F}_b) Dec(Fa,Fb) 采用一对 ViT 模块，为每张图像生成像素级点映射 X \mathbf{X} X 以及局部特征图 D \mathbf{D} D。

A. MASt3R 为什么能当"图像匹配器"？它输出了什么？

A1）你要解决的问题是什么？

你有两张图：

I a \mathbf{I}_a Ia：比如真实图里抠出来的目标区域 I m \mathbf{I}_m Im

I b \mathbf{I}b Ib：比如某张模板图 I i , k \mathbf{I}{i,k} Ii,k

你想知道：

真实图上的这个像素点，对应模板图上的哪个像素点？

这叫 像素级匹配 / correspondence。有了对应关系，你才能把模板里的"像素→3D点"映射搬到真实图上，最终才能解位姿。

A2）MASt3R 的核心结构：Enc + Dec（你别被公式吓到）

文中把 MASt3R 写成：

f ( I a , I b ) = Dec ( Enc ( I a ) , Enc ( I b ) ) \mathbf{f}(\mathbf{I}_a,\mathbf{I}_b)=\text{Dec}(\text{Enc}(\mathbf{I}_a),\text{Enc}(\mathbf{I}_b)) f(Ia,Ib)=Dec(Enc(Ia),Enc(Ib))

这句话翻译成大白话就是：

先用同一个编码器分别把两张图变成"特征"，再用解码器把两张图的特征结合起来，输出匹配相关的东西。

1）Enc：孪生（Siamese）ViT 编码器

"孪生"意思是：两张图用同一套网络（权重共享）

ViT（Vision Transformer）会把图切成很多 patch，再变成 token。

文里说 Enc 输出 F ∈ R N × d \mathbf{F}\in\mathbb{R}^{N\times d} F∈RN×d：

N = w × h N=w\times h N=w×h：token 数量（把特征图理解成 w × h w\times h w×h 个位置）

d d d：每个 token 的维度（每个位置一个 d d d 维向量）

你可以把 F \mathbf{F} F 想成一张"特征地图"：

图上每个位置都有一个向量，描述这个位置长什么样、几何上像什么。

2）Dec：一对 ViT 模块（把两张图联系起来）

解码器吃进去 F a , F b \mathbf{F}_a,\mathbf{F}_b Fa,Fb，输出两类东西：

X \mathbf{X} X：像素级点映射（point map） 你可以直觉理解为：它在告诉你"这张图每个像素对应的局部三维信息/几何点"。（原文说 MASt3R 同时做局部三维重建 + 像素级匹配，所以它会产出与3D有关的映射。）

D \mathbf{D} D：局部特征图（local descriptor map） 这个最关键：

以后所有"谁跟谁匹配""相似度多少"都是在 D \mathbf{D} D 上算的。

所以对两张图，你会得到：

D a \mathbf{D}_a Da、 D b \mathbf{D}_b Db：两张图各自的局部特征图

（以及 X a \mathbf{X}_a Xa、 X b \mathbf{X}_b Xb 这类点映射信息）

利用这些局部特征表示，图像之间的对应关系通过 fastNN 算法 [24] 来确定。该算法首先在均匀的像素网格上初始化种子点，并通过迭代细化这些种子，从而在特征图 D a \mathbf{D}_a Da 与 D b \mathbf{D}_b Db 之间高效建立高质量的双向对应关系。通过这一过程，fastNN 能够在不同图像之间准确对齐关键特征。最终得到的 I a \mathbf{I}_a Ia 与 I b \mathbf{I}b Ib 之间的双向像素匹配对表示为
M a , b = { ( y a c , y b c ) } c = 1 ∣ M a , b ∣ M{a,b} = \{(\mathbf{y}a^c, \mathbf{y}b^c)\}{c=1}^{|M{a,b}|} Ma,b={(yac,ybc)}c=1∣Ma,b∣，其中 y a c \mathbf{y}_a^c yac 和 y b c ∈ N 2 \mathbf{y}_b^c \in \mathbb{N}^2 ybc∈N2 分别表示在两幅图像中匹配像素的坐标。

B. fastNN 是怎么从 D a \mathbf{D}_a Da 和 D b \mathbf{D}_b Db 里找对应关系的？

你现在有两张图的局部特征图：

D a \mathbf{D}_a Da：真实图（或目标区域）的特征

D b \mathbf{D}_b Db：模板图的特征

你要找匹配点对：

真实图哪个点 ↔ 模板图哪个点

但如果你暴力对每个像素做最近邻搜索，会非常慢（ H W HW HW 级别像素太多）。所以他们用 fastNN：

B1）fastNN 的直觉过程（"从粗到细找匹配"）

fastNN 干的事是：

先在图上均匀撒一些种子点 不用全像素，一开始只取一个稀疏网格（比如每隔几像素取一个点），这样快。

对每个种子点，去另一张图里找特征最像的点 "最像"就是特征向量距离最近 / 相似度最高。

迭代细化 找到了粗匹配后，再在附近小范围精调，把匹配从粗变细、从少变多、从不准变更准。

做双向匹配（bidirectional）

A→B 找一遍

B→A 再找一遍
只保留一致的匹配，质量更高。

所以 fastNN 输出的是：高质量、双向一致、计算还快 的像素匹配集合。

C. 匹配集合 M a , b M_{a,b} Ma,b 是什么？（把符号讲到你不会混）

最终得到的匹配被写成：

M a , b = { ( y a c , y b c ) } c = 1 ∣ M a , b ∣ M_{a,b} = \{(\mathbf{y}a^c, \mathbf{y}b^c)\}{c=1}^{|M{a,b}|} Ma,b={(yac,ybc)}c=1∣Ma,b∣

你别怕它长，它就是一个"点对列表"：

c c c 是第 c c c 个匹配点对

y a c ∈ N 2 \mathbf{y}_a^c\in\mathbb{N}^2 yac∈N2：在图 a a a 里的像素坐标（就是二维坐标，比如 (u,v)）

y b c ∈ N 2 \mathbf{y}_b^c\in\mathbb{N}^2 ybc∈N2：在图 b b b 里的像素坐标

∣ M a , b ∣ |M_{a,b}| ∣Ma,b∣：一共有多少对匹配

一句话： M a , b M_{a,b} Ma,b 就是一张表，表里每一行写着："图 a 的这个像素 ↔ 图 b 的那个像素"。

Similarity-Based Template Selection（基于相似度的模板选择） 不同于需要数百个模板的方法 [22, 36, 41]，Pos3R 仅需四十个模板即可完成模板选择，从而显著降低了选择过程的复杂度。我们并未依赖经过训练的模板选择网络，而是采用一种基于匹配对应关系相似度的、简单且无需训练的方法。具体而言，给定目标分割区域 I m \mathbf{I}m Im 以及一组八个基础模板 { I i } i = 1 8 \{\mathbf{I}i\}{i=1}^8 {Ii}i=18，并为每个模板引入旋转增强 { I i , k } k = 1 5 \{\mathbf{I}{i,k}\}_{k=1}^5 {Ii,k}k=15，我们通过计算目标区域与每个模板之间的对应关系来确定用于位姿估计的最相似模板。

D. 为什么要"模板选择"？（40 张模板里选最像的）

你现在不是只有一张模板，而是 40 张模板（8个视角×5个轴向旋转）。你不可能随便挑一张就直接PnP，否则可能离真实姿态太远、匹配质量会掉。所以需要"模板选择"。关键点：他们不训练选择网络。而是用一个非常朴素但有效的原则：

哪张模板跟真实目标区域的"匹配关系"更好、特征更相似，它就更可能是正确姿态附近的模板。

对于每个旋转增强模板 I i , k \mathbf{I}{i,k} Ii,k，我们获取目标区域 I m \mathbf{I}m Im 与模板 I i , k \mathbf{I}{i,k} Ii,k 之间的双向像素匹配对，其表示为 M m , i , k = ( y m p , y i , k p ) p = 1 ∣ M m , i , k ∣ M{m,i,k} = {(\mathbf{y}m^p, \mathbf{y}{i,k}^p)}{p=1}^{|M{m,i,k}|} Mm,i,k=(ymp,yi,kp)p=1∣Mm,i,k∣。其中 M m , i , k M_{m,i,k} Mm,i,k 表示 I m \mathbf{I}m Im 与 I i , k \mathbf{I}{i,k} Ii,k 之间所有双向匹配像素对的集合， y m p \mathbf{y}m^p ymp 和 y i , k p ∈ N 2 \mathbf{y}{i,k}^p \in \mathbb{N}^2 yi,kp∈N2 分别表示目标区域与模板中匹配像素的坐标。

E. Pos3R 的模板选择怎么做？（一步一步走）

E1）对每个模板都做一次匹配，得到 M m , i , k M_{m,i,k} Mm,i,k

这里 m m m 表示目标区域（mask 后的物体区域）：

M m , i , k = ( y m p , y i , k p ) p = 1 ∣ M m , i , k ∣ M_{m,i,k} = {(\mathbf{y}m^p, \mathbf{y}{i,k}^p)}{p=1}^{|M{m,i,k}|} Mm,i,k=(ymp,yi,kp)p=1∣Mm,i,k∣`

含义同样是"点对列表"：

y m p \mathbf{y}_m^p ymp：目标区域里的第 p p p 个匹配像素点

y i , k p \mathbf{y}{i,k}^p yi,kp：模板 I i , k \mathbf{I}{i,k} Ii,k 里与之对应的像素点

总共有 ∣ M m , i , k ∣ |M_{m,i,k}| ∣Mm,i,k∣ 对匹配

注意：这一步等价于：

对每张模板，问 MASt3R："你觉得它和目标区域哪些像素互相对应？"

E2）在每个匹配点对上，拿出两边的局部特征向量

对于每一对匹配像素 ( y m p , y i , k p ) (\mathbf{y}m^p,\mathbf{y}{i,k}^p) (ymp,yi,kp)：

从目标区域的特征图 D m \mathbf{D}_m Dm 取出该点的特征向量： f m p \mathbf{f}_m^p fmp

从模板的特征图 D i , k \mathbf{D}{i,k} Di,k 取出对应点的特征向量： f i , k p \mathbf{f}{i,k}^p fi,kp

你可以把 f \mathbf{f} f 当成：

"这个像素附近长啥样/几何像啥"的指纹向量。

对于 M m , i , k M_{m,i,k} Mm,i,k 中的每一对匹配像素 ( y m p , y i , k p ) (\mathbf{y}m^p, \mathbf{y}{i,k}^p) (ymp,yi,kp)，我们从 MASt3R 生成的特征图 D m \mathbf{D}m Dm 和 D i , k \mathbf{D}{i,k} Di,k 中提取对应的局部特征。具体而言，我们从 D m \mathbf{D}m Dm 中提取目标区域坐标 y m p \mathbf{y}m^p ymp 处的特征向量 f m p \mathbf{f}m^p fmp，并从 D i , k \mathbf{D}{i,k} Di,k 中提取模板坐标 y i , k p \mathbf{y}{i,k}^p yi,kp 处的特征向量 f i , k p \mathbf{f}{i,k}^p fi,kp。我们将每一对匹配特征的相似度定义为
S ( f m p , f i , k p ) = f m p ⋅ f i , k p , S(\mathbf{f}m^p, \mathbf{f}{i,k}^p) = \mathbf{f}m^p \cdot \mathbf{f}{i,k}^p, S(fmp,fi,kp)=fmp⋅fi,kp,

其中 ⋅ \cdot ⋅ 表示点积运算。

E3）每对特征怎么计算相似度？用点积

他们定义：

S ( f m p , f i , k p ) = f m p ⋅ f i , k p , S(\mathbf{f}m^p, \mathbf{f}{i,k}^p) = \mathbf{f}m^p \cdot \mathbf{f}{i,k}^p, S(fmp,fi,kp)=fmp⋅fi,kp,

点积的直觉是：

两个向量方向越一致（越相像），点积越大

两个向量不相像，点积就小甚至负

所以这就是一个非常标准的"特征相似度"定义。

为计算目标分割区域 I m \mathbf{I}m Im 与每个模板变体 I i , k \mathbf{I}{i,k} Ii,k 之间的整体相似度，我们对所有匹配对的相似度进行聚合，具体如下：

sim ( I m , I i , k ) = ∑ p = 1 ∣ M m , i , k ∣ S ( f m p , f i , k p ) . (1) \text{sim}(\mathbf{I}m, \mathbf{I}{i,k}) = \sum_{p=1}^{|M_{m,i,k}|} S(\mathbf{f}m^p, \mathbf{f}{i,k}^p). \tag{1} sim(Im,Ii,k)=p=1∑∣Mm,i,k∣S(fmp,fi,kp).(1)

其中 M m , i , k M_{m,i,k} Mm,i,k 表示 I m \mathbf{I}m Im 与 I i , k \mathbf{I}{i,k} Ii,k 之间的所有匹配对集合。在计算完每个 sim ( I m , I i , k ) \text{sim}(\mathbf{I}m, \mathbf{I}{i,k}) sim(Im,Ii,k) 后，我们选择相似度得分最高的模板：

( i opt , k opt ) = arg,max ⁡ i ∈ { 1 , ... , 8 } , k ∈ { 1 , ... , 5 } sim ( I m , I i , k ) . (2) (i_{\text{opt}}, k_{\text{opt}}) = \underset{i \in \{1,\dots,8\}, k \in \{1,\dots,5\}}{\operatorname{arg,max}} \text{sim}(\mathbf{I}m, \mathbf{I}{i,k}). \tag{2} (iopt,kopt)=i∈{1,...,8},k∈{1,...,5}arg,maxsim(Im,Ii,k).(2)

最终选定的模板 I i opt , k opt \mathbf{I}{i{\text{opt}}, k_{\text{opt}}} Iiopt,kopt 被作为与目标分割区域最接近的匹配，用于后续的位姿估计过程。

E4）整张模板的总相似度怎么来？把所有匹配点的相似度加起来（式(1)）

sim ( I m , I i , k ) = ∑ p = 1 ∣ M m , i , k ∣ S ( f m p , f i , k p ) . (1) \text{sim}(\mathbf{I}m, \mathbf{I}{i,k}) = \sum_{p=1}^{|M_{m,i,k}|} S(\mathbf{f}m^p, \mathbf{f}{i,k}^p). \tag{1} sim(Im,Ii,k)=p=1∑∣Mm,i,k∣S(fmp,fi,kp).(1)

你把它理解成：

这张模板如果真的和目标区域很像，那么它会产生很多高质量匹配点，而且每对匹配的特征也很相似。于是"相似度总和"就会很大。

这里"求和"的效果很重要：它同时奖励两件事：

匹配点多（ ∣ M ∣ |M| ∣M∣ 大，说明对得上很多地方）

每个匹配点相似度高（说明对得更准）

所以它既考虑了"数量"，又考虑了"质量"。

E5）从 40 张里选谁？选 sim 最大的（式(2)）

( i opt , k opt ) = arg,max ⁡ i ∈ { 1 , ... , 8 } , k ∈ { 1 , ... , 5 } sim ( I m , I i , k ) . (2) (i_{\text{opt}}, k_{\text{opt}}) = \underset{i \in \{1,\dots,8\}, k \in \{1,\dots,5\}}{\operatorname{arg,max}} \text{sim}(\mathbf{I}m, \mathbf{I}{i,k}). \tag{2} (iopt,kopt)=i∈{1,...,8},k∈{1,...,5}arg,maxsim(Im,Ii,k).(2)

这句话就是：

8×5 共40张模板，全算一遍 sim，谁最大就选谁。

选出来的模板 I i opt , k opt \mathbf{I}{i{\text{opt}},k_{\text{opt}}} Iiopt,kopt 就被认为"最接近真实物体姿态"，用来做后续位姿估计（PnP）。

3.2.3. Pose Fitting

前一节你做了模板选择，找到了最像的模板：

I i opt , k opt \mathbf{I}{i{\text{opt}}, k_{\text{opt}}} Iiopt,kopt

这意味着：

这张模板的视角/旋转最接近真实物体当前姿态，因此用它来建立几何对应最靠谱。

接下来本节要做的事非常明确：

用"真实图中的2D点"与"CAD模型上的3D点"的对应关系，算出物体相对相机的位姿 T m = ( R m , t m ) \mathbf{T}_m=(\mathbf{R}_m,\mathbf{t}_m) Tm=(Rm,tm)。

在选定合适的模板 I i opt , k opt \mathbf{I}{i{\text{opt}}, k_{\text{opt}}} Iiopt,kopt 后，我们继续估计位姿 T m = ( R m , t m ) \mathbf{T}_m = (\mathbf{R}_m, \mathbf{t}_m) Tm=(Rm,tm)，其中 R m \mathbf{R}m Rm 是三维旋转矩阵， t m \mathbf{t}m tm 是三维平移向量，用于将物体从模型坐标系变换到相机坐标系。该过程依赖一组 2D--3D 对应关系 C t final = { ( y m j , P j ) } j = 1 ∣ M ∣ \mathcal{C}{t{\text{final}}} = \{(\mathbf{y}m^j, \mathbf{P}^j)\}{j=1}^{|M|} Ctfinal={(ymj,Pj)}j=1∣M∣，其中 y m j ∈ R 2 \mathbf{y}_m^j \in \mathbb{R}^2 ymj∈R2 表示目标分割区域 I m \mathbf{I}_m Im 中匹配像素的坐标， P j ∈ R 3 \mathbf{P}^j \in \mathbb{R}^3 Pj∈R3 表示从所选模板得到的、位于模型坐标系中的对应三维点，共有 ∣ M ∣ |M| ∣M∣ 对。为求得 T m \mathbf{T}_m Tm，我们求解透视 n 点（Perspective-n-Point, PnP）问题，其目标是最小化重投影误差：

arg min ⁡ R m , t m ∑ j = 1 ∣ M ∣ ∣ ∣ y m j − π ( R m P j + t m ) ∣ ∣ 2 , (3) \operatorname*{arg\ min}_{\mathbf{R}_m, \mathbf{t}m} \sum{j=1}^{|M|} \left|| \mathbf{y}_m^j - \pi(\mathbf{R}_m \mathbf{P}^j + \mathbf{t}_m) |\right|^2, \tag{3} Rm,tmarg minj=1∑∣M∣ ∣ymj−π(RmPj+tm)∣ 2,(3)

其中 π \pi π 是投影函数，用于根据相机内参将三维点映射到二维图像点。

2）最关键的输入：2D--3D 对应关系 C t final \mathcal{C}{t{\text{final}}} Ctfinal 是什么？

他们写：

C t final = ( y m j , P j ) j = 1 ∣ M ∣ \mathcal{C}{t{\text{final}}}={(\mathbf{y}m^j,\mathbf{P}^j)}{j=1}^{|M|} Ctfinal=(ymj,Pj)j=1∣M∣

这其实就是一个"配对表格"，每一行是一对：

y m j ∈ R 2 \mathbf{y}_m^j\in\mathbb{R}^2 ymj∈R2：真实图（目标区域 I m \mathbf{I}_m Im）里的一个像素坐标（二维点）

P j ∈ R 3 \mathbf{P}^j\in\mathbb{R}^3 Pj∈R3：CAD 模型坐标系里的一个三维点（3D点）

∣ M ∣ |M| ∣M∣：一共有多少对

一句话：

"真实图上这个像素点"对应"CAD 模型上这个3D点"。

2.1 这对对应是怎么来的？（把前面三节串起来）

你别把它当作凭空出现，它来自之前两步：

MASt3R 给了你：真实图像素 ↔ 模板图像素

模板渲染时你记录了：模板像素 ↔ CAD 3D点

合起来就得到：真实像素 ↔ CAD 3D点

所以 C t final \mathcal{C}{t{\text{final}}} Ctfinal 是"把匹配结果变成几何解算可用数据"的关键产物。

3）位姿 T m = ( R m , t m ) \mathbf{T}_m=(\mathbf{R}_m,\mathbf{t}_m) Tm=(Rm,tm) 到底代表什么？

这也是常见卡点，我把它讲得非常直白：

R m \mathbf{R}_m Rm：一个 3 × 3 3\times 3 3×3 的旋转矩阵作用：把模型坐标系里的点"转到相机坐标系的方向"

t m \mathbf{t}_m tm：一个 3 维向量作用：把模型坐标系里的点"平移到相机坐标系的位置"

合起来就是：

把 CAD 模型里一个点 P j \mathbf{P}^j Pj 变到相机坐标系：
X j = R m P j + t m \mathbf{X}^j=\mathbf{R}_m\mathbf{P}^j+\mathbf{t}_m Xj=RmPj+tm

也就是"模型点在相机眼里在哪里"。

4）PnP 在解什么？式(3) 的意思是什么？

他们说解 PnP：最小化重投影误差：

arg min ⁡ R m , t m ∑ j = 1 ∣ M ∣ ∣ ∣ y m j − π ( R m P j + t m ) ∣ ∣ 2 , (3) \operatorname*{arg\ min}_{\mathbf{R}_m, \mathbf{t}m} \sum{j=1}^{|M|} \left|| \mathbf{y}_m^j - \pi(\mathbf{R}_m \mathbf{P}^j + \mathbf{t}_m) |\right|^2, \tag{3} Rm,tmarg minj=1∑∣M∣ ∣ymj−π(RmPj+tm)∣ 2,(3)

你别怕，这个式子就是在说一件事：

我猜一个位姿 ( R m , t m ) (\mathbf{R}_m,\mathbf{t}_m) (Rm,tm)，

把 CAD 的 3D 点变到相机坐标系后，再通过相机投影函数 π \pi π 投到图像上，得到一个"预测的2D位置"。

这个预测位置应该尽量贴近真实图上的2D点 y m j \mathbf{y}_m^j ymj。

所以我们让所有点的误差平方和最小。

4.1 投影函数 π \pi π 是干嘛的？

π \pi π 就是"相机怎么把 3D 点变成 2D 像素"的规则（用内参 K \mathbf{K} K）。

直觉公式是：

3D点 ( X , Y , Z ) (X,Y,Z) (X,Y,Z) 先做透视除法变成 ( X / Z , Y / Z ) (X/Z, Y/Z) (X/Z,Y/Z)

再乘内参得到像素 ( u , v ) (u,v) (u,v)

你不需要背具体公式，只要记住：

π \pi π 把"相机坐标系里的3D点"映射成"图像上的像素点"。

4.2 什么是"重投影误差"？

对于每一对对应：

真实的像素位置： y m j \mathbf{y}_m^j ymj

用你猜的位姿投影出来的像素位置： π ( R m P j + t m ) \pi(\mathbf{R}_m\mathbf{P}^j+\mathbf{t}_m) π(RmPj+tm)

两者的距离就是重投影误差。误差越小，说明你猜的位姿越对。

为增强对离群点的鲁棒性，我们采用高效 PnP（EPnP）算法 [23]，并结合基于 RANSAC 的拟合策略 [11]。在该策略中，我们从 C t final \mathcal{C}{t{\text{final}}} Ctfinal 中随机抽取四组对应关系形成子集，并迭代地应用 PnP，从而生成多个位姿假设。对于每个假设，我们统计内点数量，内点定义为重投影误差小于预设阈值 ϵ \epsilon ϵ 的对应关系：

inliers = ∣ { j : ∣ ∣ y m j − π ( R m P j + t m ) ∣ < ϵ } ∣ ∣ . (4) \text{inliers} = \left| \left\{ j : \left|| \mathbf{y}_m^j - \pi(\mathbf{R}_m \mathbf{P}^j + \mathbf{t}_m) \right| < \epsilon \right\} |\right|. \tag{4} inliers= {j: ∣ymj−π(RmPj+tm) <ϵ}∣ .(4)

最终，我们将内点数量最多的假设选作最终的粗位姿估计 T m \mathbf{T}_m Tm。

5）为什么要 RANSAC？因为匹配里一定有"错的对应"（离群点）

哪怕 MASt3R 很强，匹配里仍会存在：

错配（背景点、重复纹理、遮挡导致的误配）

模板与真实域差异导致的少量错误

如果你把这些错点全喂给 PnP，PnP 会被带偏，算出一个离谱的位姿。

所以作者说：

为增强对离群点鲁棒性，我们用 EPnP + RANSAC。

6）EPnP 是什么？为什么用它？

PnP 有很多解法，EPnP（Efficient PnP）是一种经典高效算法。你只要抓住这层意思就够：

它能在给定一堆 2D-3D 对应时，快速算出一个候选位姿

很适合在 RANSAC 里"反复试很多次"（因为 RANSAC 会跑很多轮）

所以这里用 EPnP 的目的很明确：快。

7）RANSAC 的流程：为什么"随机抽四组对应关系"？

这里是本节最核心的"算法结构"。我用一步一步讲清楚：

7.1 为什么抽 4 对？

文里说"随机抽取四组对应关系形成子集"。原因是：

PnP 理论上最少需要 4 对 2D-3D 对应才能解出位姿（经典最小集思想）

用最小集做假设生成（hypothesis generation）是 RANSAC 的标准套路：小集合更可能抽到"全是正确点"的组合。

所以每一轮 RANSAC：

从 C ∗ t ∗ final \mathcal{C}*{t*{\text{final}}} C∗t∗final 随机抽 4 对点

用 EPnP 算出一个候选位姿 ( R m , t m ) (\mathbf{R}_m,\mathbf{t}_m) (Rm,tm)

这就是"生成一个假设"。

7.2 怎么判断这个假设好不好？看"内点数量"是多少

有了候选位姿后，不是立刻相信它，而是拿它去检查所有对应点：

对第 j j j 个对应点，算重投影误差：

∣ y m j − π ( R m P j + t m ) ∣ \left|\mathbf{y}_m^j-\pi(\mathbf{R}_m\mathbf{P}^j+\mathbf{t}_m)\right| ymj−π(RmPj+tm)

如果这个误差小于阈值 ϵ \epsilon ϵ，就认为这对对应是内点（inlier），也就是"符合这个位姿假设的可信点"。

这就是式(4)：

KaTeX parse error: Expected '}', got '\right' at position 113: ...ight|<\epsilon \̲r̲i̲g̲h̲t̲}\right| \tag{4...

翻译成大白话：

内点数 = "有多少对点，在这个位姿下投影误差足够小"。

8）最终怎么得到 T m \mathbf{T}_m Tm？------选"内点最多"的假设

RANSAC 会跑很多轮，每轮都得到一个候选位姿和对应的内点数。

最后一步非常简单：

选内点数最多的那一个候选位姿，作为最终粗位姿估计 T m \mathbf{T}_m Tm。

为什么"内点最多"就最好？直觉是：

正确位姿会让大量真实对应点都对齐（误差小）

错误位姿只能对齐少数点（误差大）

所以"最多内点"就是最稳的选择标准。

4. Experiments

在本节中，我们首先介绍实验设置（第 4.1 节）。随后，我们在 BOP 挑战赛的七个核心数据集上，将我们的方法与以往方法进行对比评估 [17]，重点考察其精度、运行效率，以及在使用预测 3D 模型时的有效性（第 4.2 节）。该评估突出了我们方法的优势及其独特贡献。最后，我们通过消融实验分析方法中不同配置对性能的影响（第 4.3 节）。

4.1. Experimental Setup

评测数据集 我们在 BOP 挑战赛的七个核心数据集上评估我们的方法 [17]，包括：LineMod Occlusion（LM-O）[3]、T-LESS [15]、TUD-L [16]、ICBIN [8]、ITODD [9]、HomebrewedDB（HB）[21] 以及 YCB-Video（YCB-V）[57]。这些数据集共包含 132 个不同物体和 19,048 个测试实例，均处于复杂、杂乱且存在部分遮挡的场景中。表 1 给出了各数据集的实例数量。值得注意的是，未见物体位姿估计任务仍然极具挑战性，且仍有较大的提升空间。

评测指标 我们采用 BOP 位姿评测协议 [17] 对 6D 物体定位进行评估，该协议通过三种误差指标衡量位姿精度：可见表面差异（VSD）、最大对称性感知表面距离（MSSD）以及最大对称性感知投影距离（MSPD）。 VSD 仅评估物体的可见部分以处理歧义问题；MSSD 在考虑全局对称性的情况下衡量三维表面偏差；MSPD 则利用投影空间中的物体对称性来评估可感知的偏差。对于某一误差指标 e e e，若 e < θ e e < \theta_e e<θe（其中 θ e \theta_e θe 为正确性阈值），则该位姿被判定为正确。每个指标 e e e 的平均召回率（Average Recall，AR），记为 AR e \text{AR}e ARe，是在不同阈值 θ e \theta_e θe（对于 VSD 还包括多种错位容忍度 τ \tau τ）下召回率的平均值。总体 AR 分数为三种指标的平均值：
AR = AR VSD + AR MSSD + AR MSPD 3 . \text{AR} = \frac{\text{AR}{\text{VSD}} + \text{AR}{\text{MSSD}} + \text{AR}{\text{MSPD}}}{3}. AR=3ARVSD+ARMSSD+ARMSPD.

位姿精化 为展示 Pos3R 能够与渲染-对比（render-and-compare）类精化技术相结合，我们将 MegaPose [22] 中的精化方法应用于我们的结果。给定输入图像和初始估计位姿，精化模块预测该初始位姿与真实位姿之间的相对变换。该精化模块在大规模数据集上训练，并结合了多种精心设计的技术 [22]。我们使用公式 (1) 中定义的相似度得分选择前 5 个模板，并对每个测试裁剪与模板对通过 EPnP 得到一个位姿估计。随后，我们利用精化模块对这五个候选位姿进行更新。

4.2. Comparison With the State of the Art

我们将 Pos3R 与无训练方法和基于训练的方法进行对比。无训练方法包括 FoundPose [41] 和 ZS6D [2]，而基于训练的方法包括 MegaPose [22]、GigaPose [39]、OSOP [48] 以及 GenFlow [34]。在位姿精化阶段，我们采用 MegaPose [22] 的精化模块。我们使用文献 [39] 提供的公开代码，并采用其默认超参数设置。

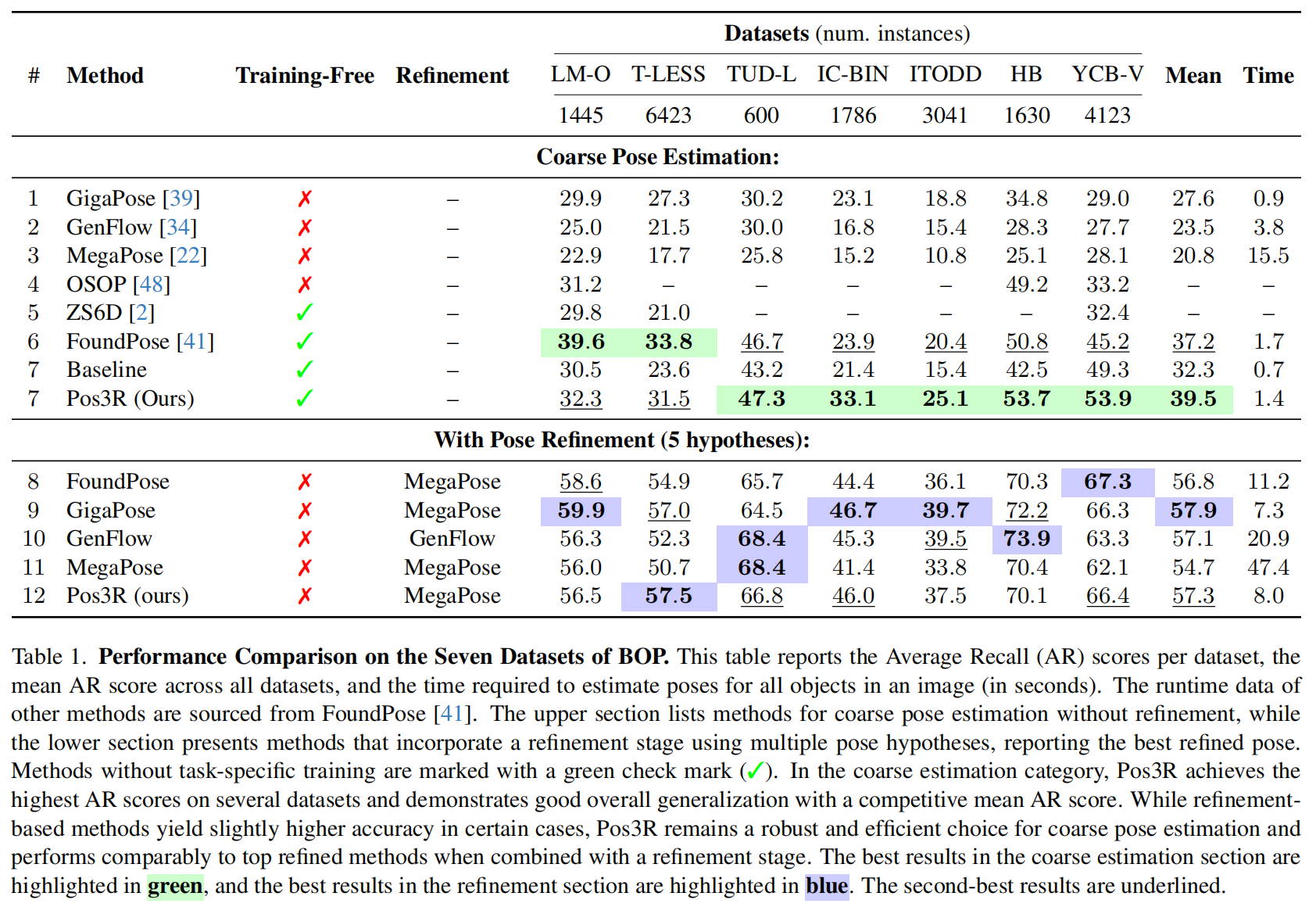
表 1 详细对比了 Pos3R 与其他领先的 6D 位姿估计方法在 BOP 挑战赛七个主要数据集上的表现。表格上半部分展示了未进行精化的粗位姿估计结果，下半部分则展示了在引入五个候选位姿进行精化后的性能。需要强调的是，位姿精化过程依赖于在大规模位姿数据集上的任务特定训练，因此并非无训练方法 [22]。

在粗位姿估计任务中，Pos3R 的性能优于其他无训练方法（包括 FoundPose 和 ZS6D），在大多数数据集上取得了最高的平均精度和稳定的优异表现。例如，Pos3R 在 TUD-L、HB 和 YCB-V 数据集上取得了最高的 AR（平均召回率），整体平均 AR 达到 39.5。这种在多样化数据集上的高性能体现了 Pos3R 在不同物体姿态和应用场景下的强泛化能力。此外，Pos3R 的运行时间仅为 1.4 秒，相比那些需要大量计算资源或并非无训练的方法，展现出显著的效率优势。

在使用 MegaPose 的精化模块后，Pos3R 依然保持了较强的竞争力。尽管 Pos3R 并非为精化过程而专门设计，但在多个数据集上，其精化后的精度可与 MegaPose 及其他经过精化的方法相当。这些结果凸显了 Pos3R 的适应性：它既能提供准确的初始位姿估计，又能从额外的精化技术中获益，显示出其在 6D 位姿估计中具备可扩展性、实用性和灵活性的潜力。

此外，我们观察到 Pos3R 在 LM-O 数据集上的竞争性精度仍存在挑战，该数据集中严重的遮挡是主要难点。遮挡会破坏初始图像匹配过程，往往导致较差的初始位姿估计，而精化方法也难以对其进行有效纠正。 FoundPose [41] 通过在模板选择中采用词袋（bag-of-words）策略来缓解这一问题，该策略在应对遮挡时表现出更强的鲁棒性。为提升在此类场景下的鲁棒性，引入 GigaPose [39] 所采用的局部对比学习方法可能是一个有前景的方向。该方法专门用于增强遮挡区域中的特征匹配能力，我们将其视为未来值得进一步探索的研究方向。

4.3. Component Analysis

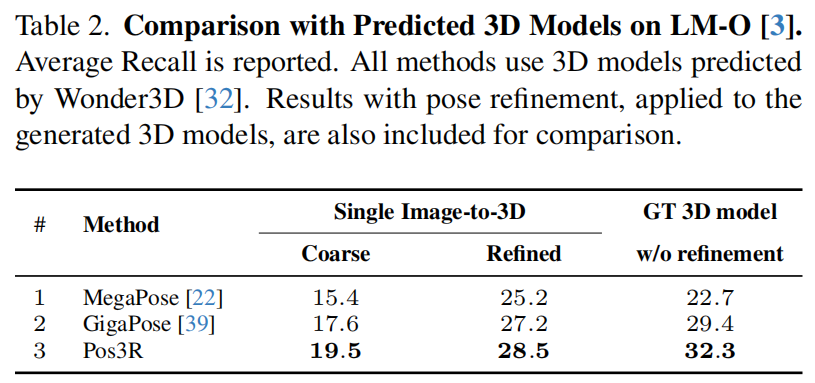
Pose Estimation Using Predicted 3D Models 使用预测 3D 模型进行位姿估计 基于模型的未见物体位姿估计方法通常需要精确且带纹理的 3D 模型。为降低这一要求，我们遵循文献 [39] 的做法，使用 Wonder3D [32] 从单张参考图像预测生成 3D 模型。预测得到的 3D 模型采用与真实标注（GT）相同的物体坐标系，从而保证坐标轴对齐。随后，我们使用这些重建得到的模型替代数据集提供的高质量 CAD 模型，对我们的方法性能进行评估。为保证公平比较，我们采用与文献 [39] 相同的实验设置，包括 Wonder3D 所使用的参考图像及后处理步骤，并在 LM-O 数据集 [3] 上报告结果。由生成的 3D 模型渲染得到的视角示例如图 3 所示。如表 2 所示，无论在位姿精化前还是精化后，Pos3R 的 AR 得分均高于 MegaPose [22] 和 GigaPose [39]，表明 Pos3R 的有效性。

Template Selection Technique 模板选择策略 在实验中，我们采用对应关系匹配相似度（公式 (1)）作为主要的模板选择方法。此外，我们还考虑了两种替代方案：1）内点数（Inliers）：基于内点数量（公式 (4)）进行模板选择； 2）置信度（Confidence）：利用 MASt3R 为每个目标分割区域--模板对提供的 3D 点映射和置信度图 [24]，并使用平均置信度得分进行选择。如图 4 所示，基于内点数的模板选择方法具有较好的效果，而基于相似度得分的选择方式性能最佳。

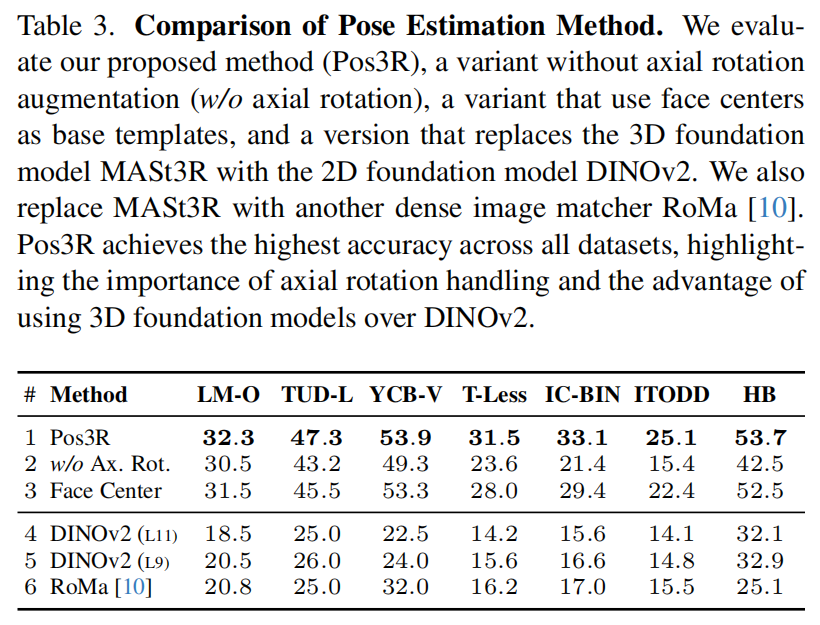
Impact of In-Plane Rotation and 3D Consistency on Pose Estimation 平面内旋转与 3D 一致性对位姿估计的影响 表 3 评估了在七个数据集上，引入平面内（轴向）旋转和 3D 一致性特征对位姿估计性能的影响。我们的方法 Pos3R（第 1 行）通过结合受控的平面内旋转以及 MASt3R 基础模型提供的 3D 一致性特征，在所有数据集上均取得了最高精度。相比之下，第 2 行展示了未引入平面内旋转的结果，此时仅使用八个基础模板来覆盖平面外旋转。此时性能显著下降，突显了处理平面内旋转对于提升对应关系质量和整体位姿精度的重要性。第 4 行和第 5 行进一步展示了一种变体，其中我们用二维基础模型 DINOv2 替换 MASt3R。尽管采用了相同的处理流程（例如同样使用 40 个模板），这一替换仍在所有数据集上导致了明显的性能下降。此外，在第 6 行中，用稠密图像匹配器 RoMa [10] 替换 MASt3R 同样导致精度下降。我们推测，MASt3R 的性能优势源于其大规模且具备 3D 感知能力的训练方式，这有助于生成更适合位姿估计任务的特征。上述分析强调了同时引入平面内旋转与 3D 一致性特征对于实现鲁棒且精确的 6D 位姿估计的重要性。

Qualitative Results of 6D Pose Estimation 6D 位姿估计的定性结果 图 5 展示了 Pos3R 在多个具有挑战性的数据集上的位姿估计结果，包括 LM-O [3]、T-LESS [15]、IC-BIN [8] 和 YCB-V [57]。 Pos3R 在多样化的物体类型、尺度和纹理条件下均表现出良好的鲁棒性，能够有效应对复杂环境。在 IC-BIN 这类高度杂乱的场景中，Pos3R 能够准确定位多个紧密排列的物体。在 T-LESS 数据集中，Pos3R 对无纹理物体同样表现良好，而这类物体由于表面特征极少，通常对视觉方法构成挑战。然而，图 5 也揭示了一个局限性：在严重遮挡的场景中（以红色叉号标记），Pos3R 的表现不佳。被遮挡物体的可见性降低会导致预测的边界框出现偏差。这一局限性表明了未来的改进方向，例如引入遮挡感知方法（如 GigaPose [39]），或利用多视角信息以增强在复杂场景下的鲁棒性。

5. Conclusion

本文提出了 Pos3R，一种无需训练、仅使用 RGB 输入的未见物体 6D 位姿估计框架。通过利用 3D 基础模型 MASt3R，Pos3R 能够生成鲁棒且具备 3D 一致性的特征，从而有效处理平面内与平面外旋转。在不依赖大规模数据集或针对特定物体训练的情况下，Pos3R 为无训练研究提供了一个强有力的基线方法。通过使用最小化的模板集合------在立方体八个顶点视角采集并加入受控的旋转变化------Pos3R 实现了准确且高效的位姿估计。 BOP 挑战赛上的实验表明，Pos3R 在粗位姿估计方面优于其他无训练方法，并且在与 MegaPose 精化模块结合时，能够取得与精化类方法相当的竞争性结果。未来工作将重点引入遮挡感知技术，以提升在遮挡场景下的鲁棒性。