BFS解决拓扑排序和FloodFill问题
拓扑排序
1.有向无环图(DAG)
此时有方向,但是没有环
入度:就是有多少节点箭头指向它
出度:就是这个节点指向了多个个节点
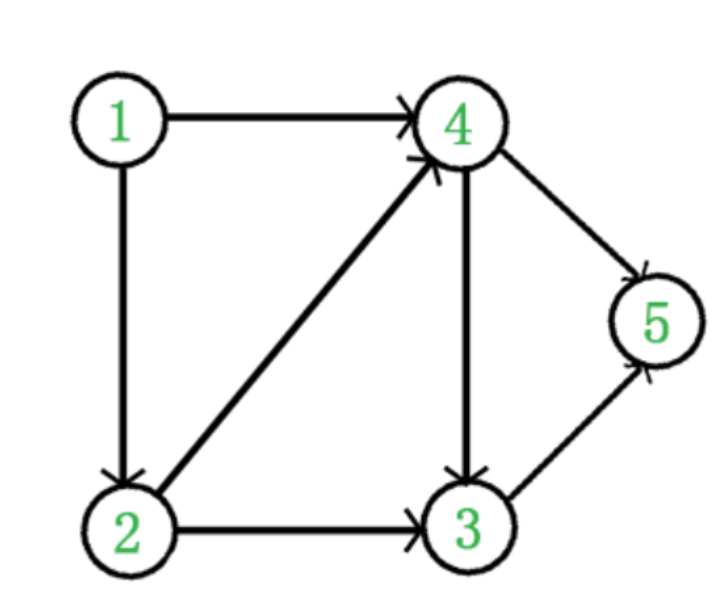
2.AOV网:顶点活动图
在这里有向无环图中,用一个顶点表示一个活动,用边表示先后顺序
3.拓扑排序
找出这里做事的先后顺序(可能有多种)
- 找到图中入度为0的点,输出
- 删除这个点对应的边
- 重复上面操作,直到图中没有点或者无入度为0的点为止(存在环)
4.实现拓扑
1.将入度为0的点放入队列中
2.当队列不为空的时候
1.拿出队头元素,放入最终结果
2.删除与该节点相连的边
3.判断:与删除相连的边的点,入度是否变成0,变成0就将其放入队列中
课程表
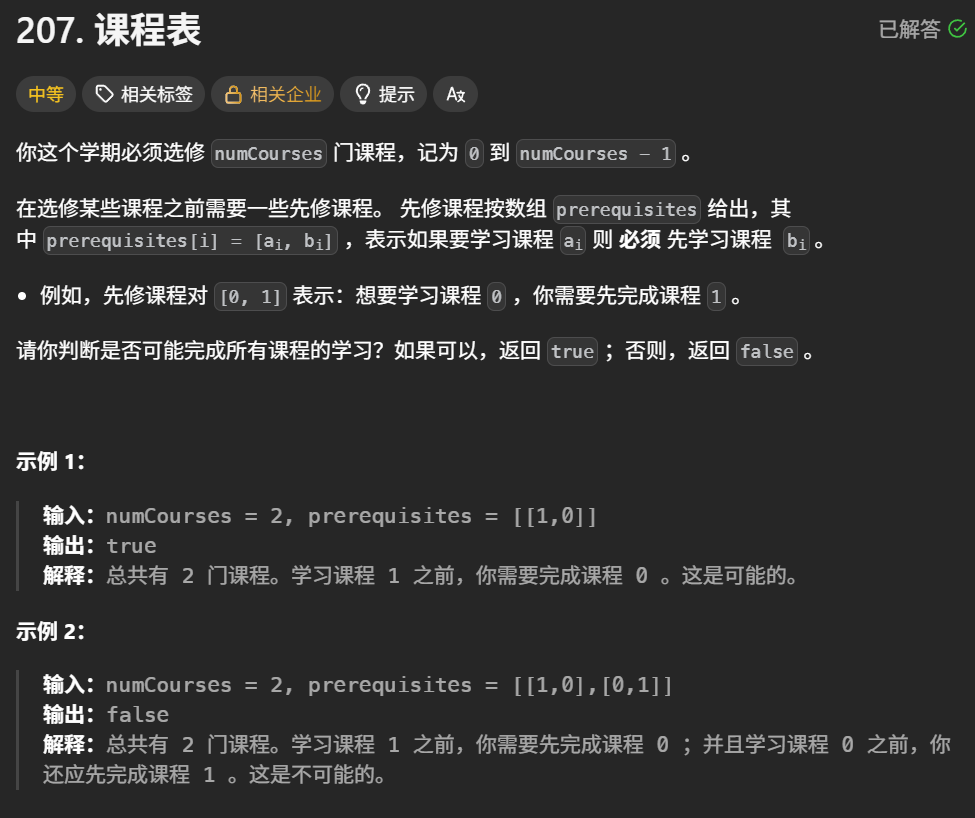
题目解析 :就是判断课程是否可以执行完,课程之间执行有一定的执行顺序
思想:拓扑排序,因为其课程之间有一定关联,此时可以使用拓扑排序建图存放其对应关系,最后进行判断其是否有环即可,有环就说明不可能完成所有课程学习
此时可以使用二维List或者Map进行建图,确保每一行都是这个节点所指向的点
此时需要一个int[ ]数组存放对应课程的入度情况,入度为0,才可以进行上课
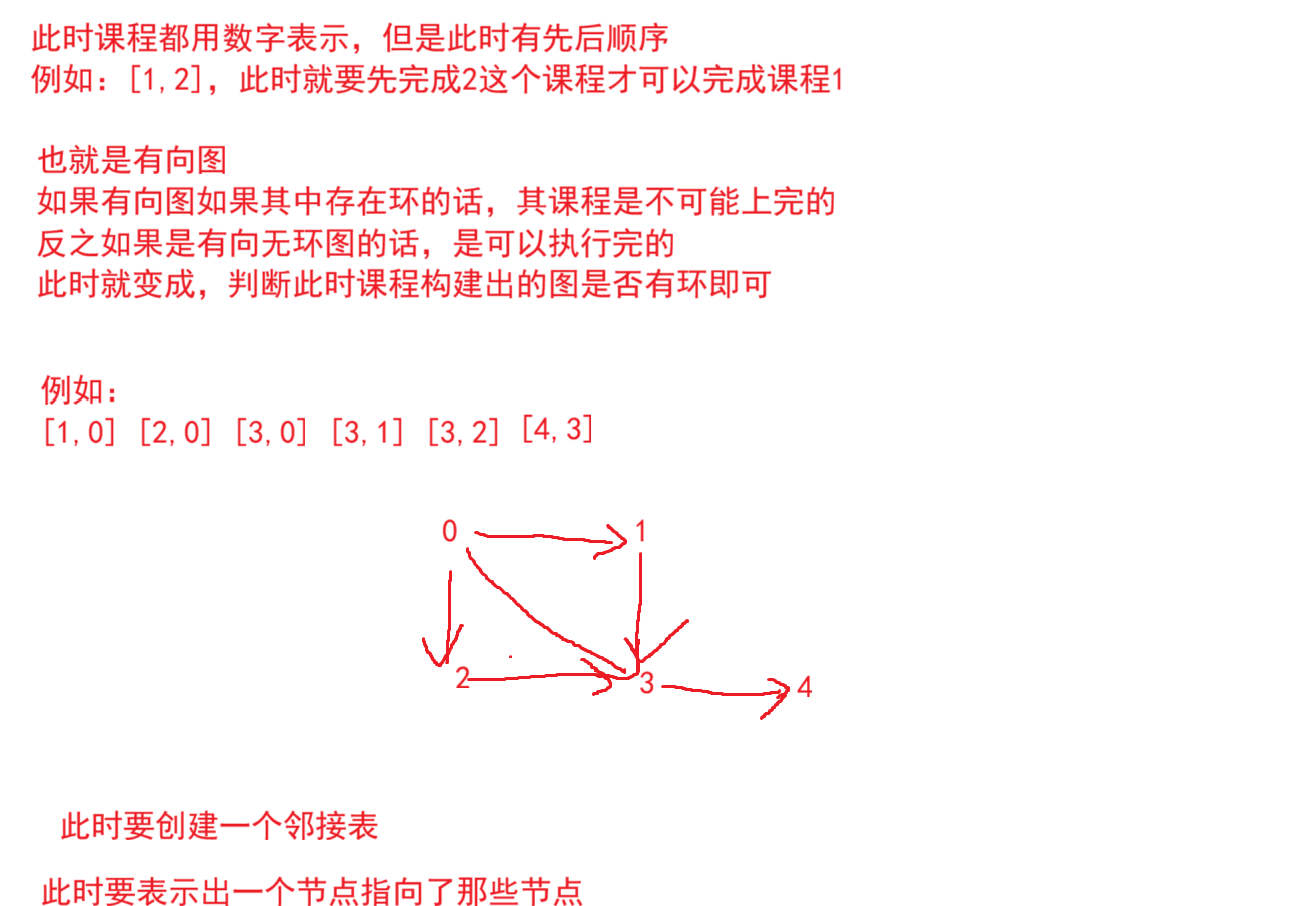

java
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
int[] in = new int[numCourses];//统计每个课程的入度情况
Map<Integer,List<Integer>> edges = new HashMap<>();//创建邻接表
//1.建图
for(int i = 0;i < prerequisites.length;i++){
int a = prerequisites[i][0];
int b = prerequisites[i][1];
//此时这里要先完整b课程,才可以完整a课程 b->a
if(!edges.containsKey(b)){
edges.put(b,new ArrayList<>());//如果没有就进行创建
}
//有的话将a加入b后面
edges.get(b).add(a);
in[a]++;//a的入度++
}
//2.将入度为0的点放入队列中
Queue<Integer> q = new LinkedList<>();
for(int i = 0;i < numCourses;i++){
if(in[i] == 0){
q.add(i);//将下标放入进去即可
}
}
//3.进行BFS遍历
while(!q.isEmpty()){
int t = q.poll();
//将其t执行的点入度都--
for(int a : edges.getOrDefault(t,new ArrayList<>())){
in[a]--;
//判断其入度是否变成0
if(in[a] == 0){
q.add(a);
}
}
}
//最后判断是否有环
//有环的话入度还存在不为0的
for(int i = 0;i < numCourses;i++){
if(in[i] != 0){
return false;
}
}
return true;
}
}课程表||
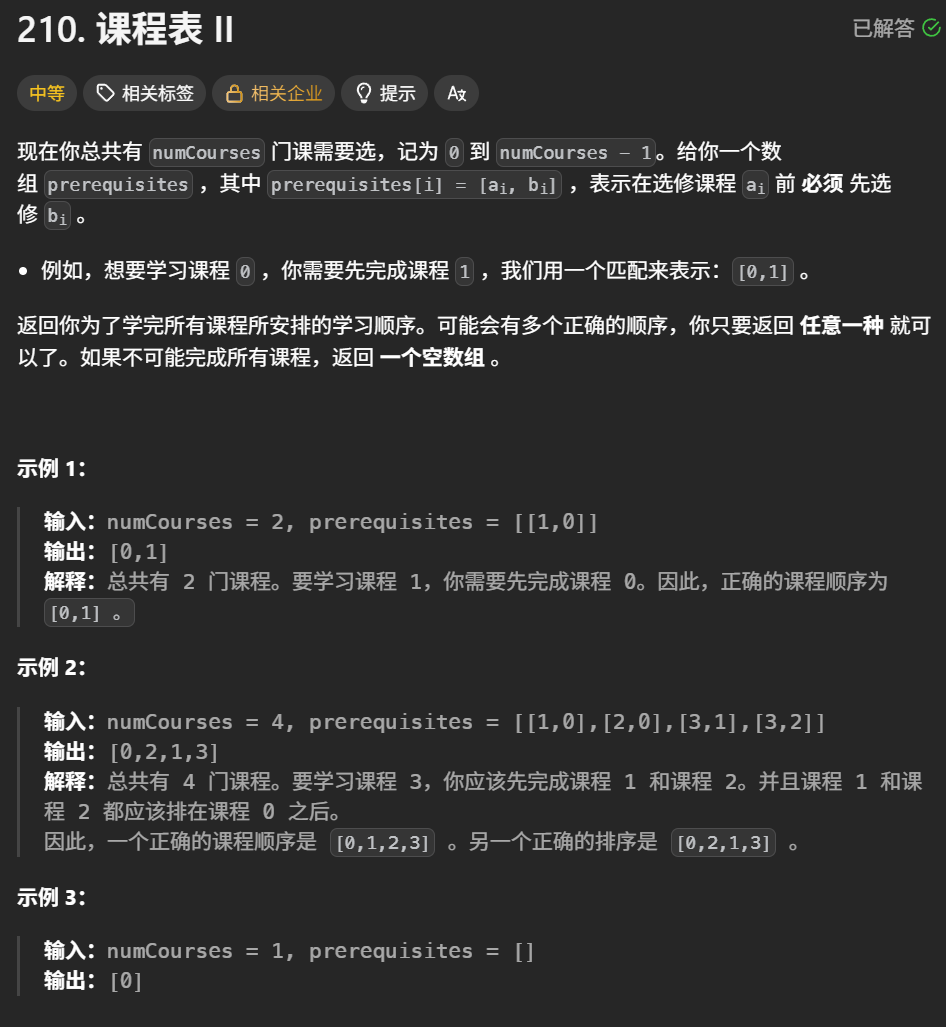
题目解析 :和上一题课程表是判断这里课程是否可以学完,此时这里无非就是判断过程中对其结果进行存放即可,虽然有多种,但是此时只需要返回一种即可
思想:就是上一题在出队列的时候,将这个出队列的元素进行放起来即可
java
//使用哈希表
class Solution {
public int[] findOrder(int numCourses, int[][] prerequisites) {
int[] in = new int[numCourses];//对应入度
int[] ret = new int[numCourses];//存放结果
Map<Integer,List<Integer>> hash = new HashMap<>();
for(int i = 0;i < prerequisites.length;i++){
int a = prerequisites[i][0];
int b = prerequisites[i][1];
//此时是b -> a
if(!hash.containsKey(b)){
hash.put(b,new ArrayList<>());
}
hash.get(b).add(a);
in[a]++;
}
//建图
//1.将所有入度为0的点放入队列中
Queue<Integer> q = new LinkedList<>();
for(int i = 0;i < numCourses;i++){
if(in[i] == 0){
q.add(i);
}
}
int count = 0;
//2.bfs
while(!q.isEmpty()){
int t = q.poll();
ret[count++] = t;
//将t后面的点入度--
for(int x : hash.getOrDefault(t,new ArrayList<>())){
in[x]--;
if(in[x] == 0){
q.add(x);
}
}
}
for(int i = 0;i < numCourses;i++){
if(in[i] != 0){
return new int[0];
}
}
return ret;
}
}
java
//使用List嵌套List
class Solution {
public int[] findOrder(int numCourses, int[][] prerequisites) {
int[] in = new int[numCourses];//对应入度
int[] ret = new int[numCourses];//存放结果
List<List<Integer>> list = new ArrayList<>();
//先将0 ~ n放入
for(int i = 0;i < numCourses;i++){
list.add(new ArrayList<>(i));
}
for(int i = 0;i < prerequisites.length;i++){
int a = prerequisites[i][0];
int b = prerequisites[i][1];
//此时是b -> a
list.get(b).add(a);
in[a]++;
}
//建图
//1.将所有入度为0的点放入队列中
Queue<Integer> q = new LinkedList<>();
for(int i = 0;i < numCourses;i++){
if(in[i] == 0){
q.add(i);
}
}
int count = 0;
//2.bfs
while(!q.isEmpty()){
int t = q.poll();
ret[count++] = t;
//将t后面的点入度--
for(int x : list.get(t)){
in[x]--;
if(in[x] == 0){
q.add(x);
}
}
}
for(int i = 0;i < numCourses;i++){
if(in[i] != 0){
return new int[0];
}
}
return ret;
}
}火星词典

题目解析 :就是给了一些单词,让我们找出这里面单词字母的字典序,外星人的字典序可能与我们不同
思想:转化成拓扑排序
1.首先根据给的单词可以确定一系列字母之间的字典序,现在只需要将这里面的字典序进行结合即可,使用拓扑排序
2.拓扑排序
依旧需要建图,也需要存放对应入度信息


java
class Solution {
Map<Character, Integer> in = new HashMap<>();//存放入度信息
Map<Character, Set<Character>> edges = new HashMap<>();//邻接表
boolean check;
public String alienOrder(String[] words) {
int n = words.length;
//将出现的字符入度全部为0
for (String s : words) {
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
in.put(ch, 0);//直接设置入度为0
}
}
//建图
//1.获取对应关系
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
add(words[i], words[j]);//将这里的信息放入邻接表中
//如果存在 abc 在 ab这种情况就是不符合,直接返回即可
if (check == true) {
return "";
}
}
}
//2.拓扑排序
Queue<Character> q = new LinkedList<>();
//将入度为0的放入队列中
for (char ch : in.keySet()) {
if (in.get(ch) == 0) {
q.add(ch);
}
}
StringBuffer ret = new StringBuffer();
while (!q.isEmpty()) {
char t = q.poll();
ret.append(t);
//检查是否有指向节点
if (edges.containsKey(t)) {
for (char ch : edges.get(t)) {
//入度--
in.put(ch, in.get(ch) - 1);
if (in.get(ch) == 0) {
q.add(ch);
}
}
}
}
for (char ch : in.keySet()) {
if (in.get(ch) != 0) {
return "";
}
}
return ret.toString();
}
public void add(String s1, String s2) {
int n = Math.min(s1.length(), s2.length());
int i = 0;
for (; i < n; i++) {
char ch1 = s1.charAt(i);
char ch2 = s2.charAt(i);
if (ch1 != ch2) {
//ch1 -> ch2
if (!edges.containsKey(ch1)) {
edges.put(ch1, new HashSet<>());
}
//此时要避免重复存
if (!edges.get(ch1).contains(ch2)) {
edges.get(ch1).add(ch2);
in.put(ch2, in.get(ch2) + 1);//入度++
}
break;
}
}
if (i == s2.length() && i < s1.length()) {
check = true;
}
}
}FloodFill问题
图像渲染

题目解析 :就是将这里面指定一个元素将其上下左右和这个一样的值,全部修改成另外一个值,并且其上下左右也可以进行上下左右进行扩展,也就是将这个一片区域都修改成color指定值
BFS:直接遍历所有下标,并且看其上下左右下标,不断进行修改,不断进行扩展延申
此时就可以使用队列放入 int[ ] 数组,对应存放行、列下标,每一次不断取出进行上下左右延申判断其是否和image[sr][sc],如果一样就继续放入队列中,不断进行操作,直到队列为空
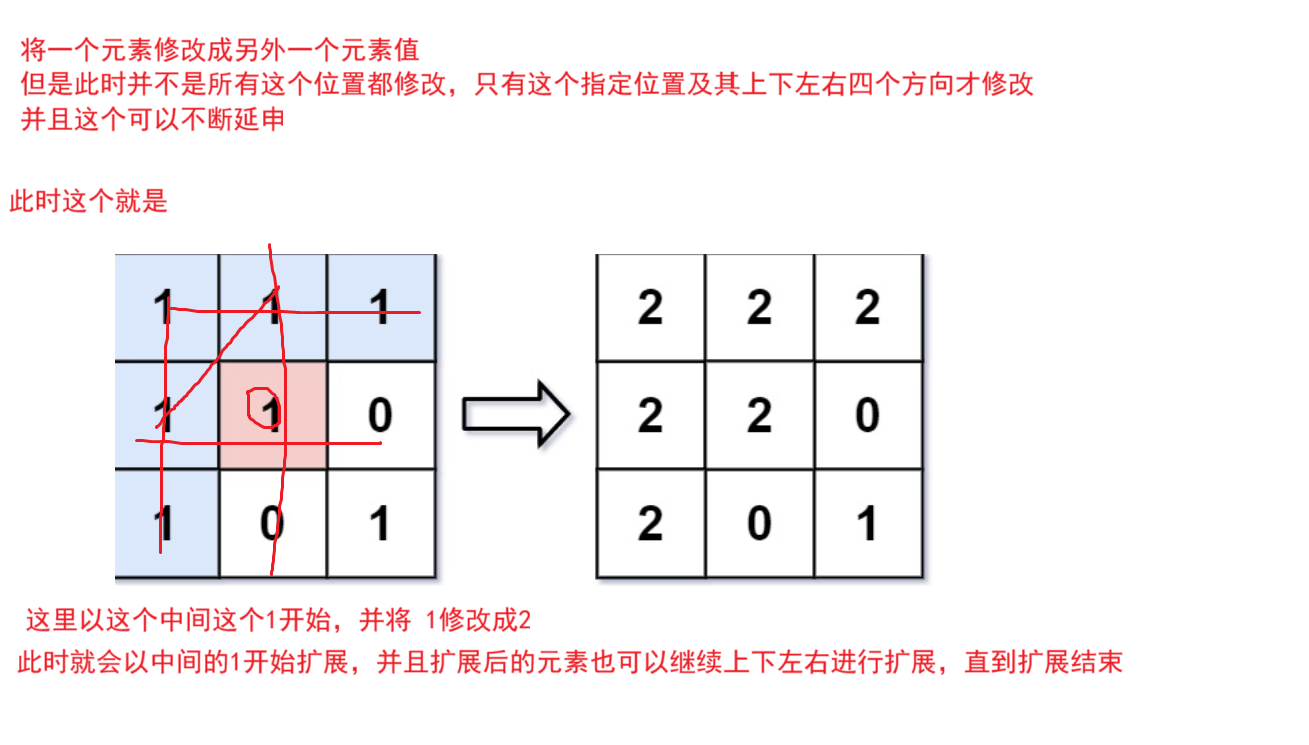
这里通过上下左右对应下标分别
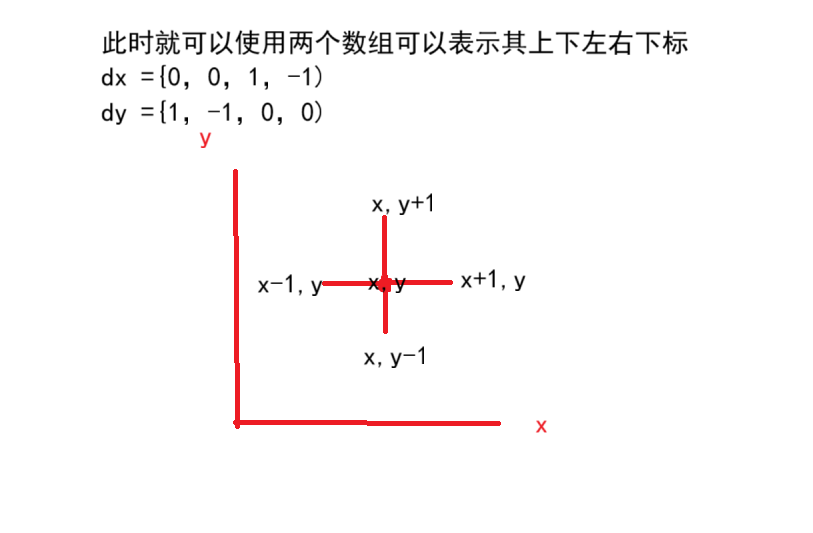
java
class Solution {
int[] dx = {0,0,1,-1};
int[] dy = {1,-1,0,0};
public int[][] floodFill(int[][] image, int sr, int sc, int color) {
int prev = image[sr][sc];
if(prev == color){
//如果要修改和修改的一样,此时就不需要修改
return image;
}
int m = image.length;
int n = image[0].length;
//存放其下标
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{sr,sc});
while(!queue.isEmpty()){
int[] tem = queue.poll();
int a = tem[0];//行
int b = tem[1];//列
//将这个颜色修改
image[a][b] = color;
//看这个位置前后左右位置
for(int i = 0;i < 4;i++){
int x = a + dx[i];
int y = b + dy[i];
if(x >=0 && x < m && y>=0 && y < n && image[x][y] == prev){
queue.add(new int[]{x,y});
}
}
}
return image;
}
}岛屿数量
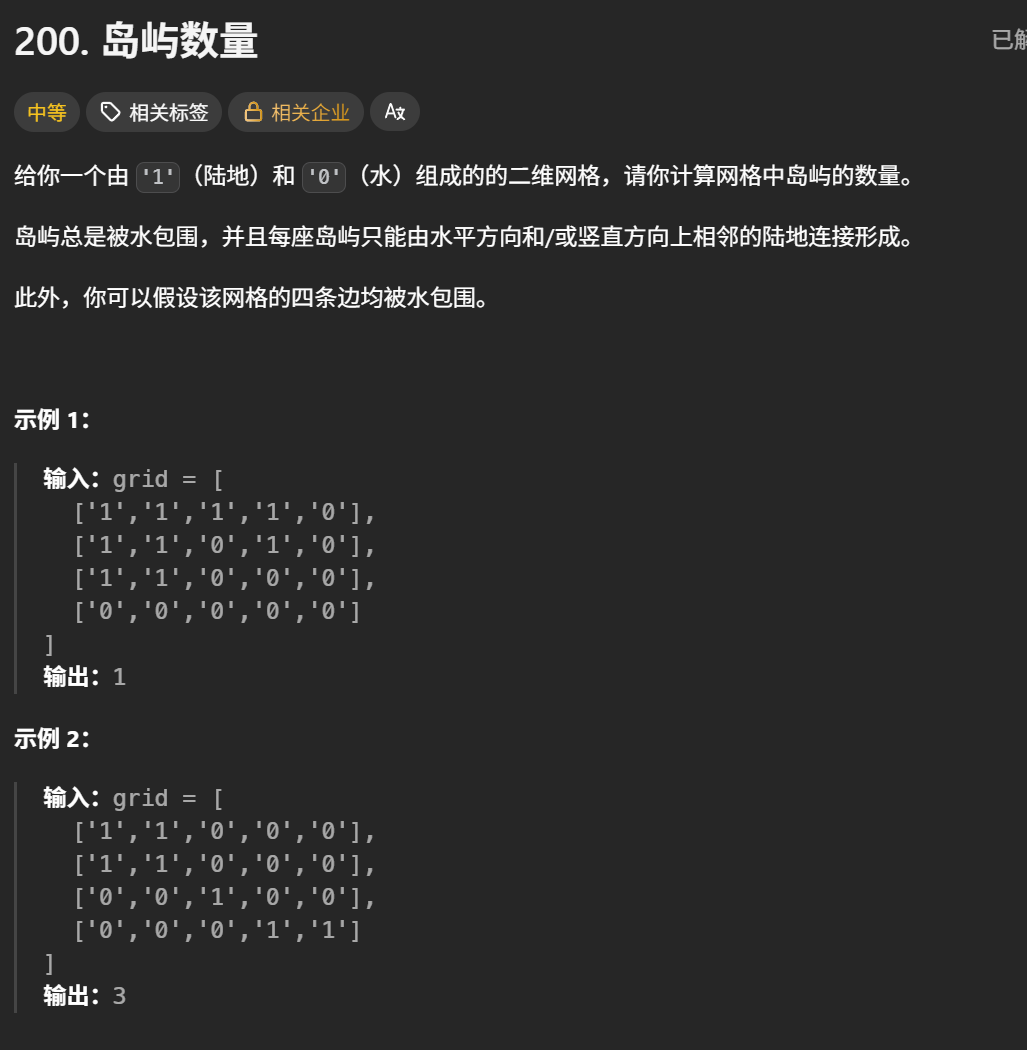
题目解析 :此时1表示岛屿,并且1的上下左右如果有1的话就会进行延申展开,最终求出有多少岛屿
BFS:遍历整个数组,但是此时一个岛屿需要延申到不能延申为止这样才成为一个岛屿 ,此时会出现问题,我们会不断扩展,后面遍历到这个位置又会让其岛屿数量+1,此时就重复统计了,这里有两种解决方案
方案一 :每次遍历过的位置,将这里的 1 修改成 0
方案二:创建一个同等规模的数组,如果统计过了就进行标记一下

java
class Solution {
int[] dx = {0,0,1,-1};
int[] dy = {1,-1,0,0};
boolean[][] visited;//标记已经遍历过的位置
int m = 0;
int n = 0;
public int numIslands(char[][] grid) {
m = grid.length;
n = grid[0].length;
visited = new boolean[m][n];
int ret = 0;
for(int i = 0;i < m;i++){
for(int j = 0;j < n;j++){
//当时1并且没有遍历过,结果++
if(grid[i][j] == '1' && visited[i][j] == false){
ret++;
dfs(grid,i,j);//将其旁边的visited都标记为遍历过
}
}
}
return ret;
}
public void dfs(char[][] grid,int i,int j){
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{i,j});
visited[i][j] = false;
while(!queue.isEmpty()){
int[] tem = queue.poll();
int a = tem[0];
int b = tem[1];
for(int k = 0; k < 4;k++){
int x = a + dx[k];
int y = b + dy[k];
if(x >= 0 && x < m && y >= 0&&y < n&&grid[x][y] == '1' && !visited[x][y]){
queue.add(new int[]{x,y});
visited[x][y] = true;
}
}
}
}
}岛屿的最大面积

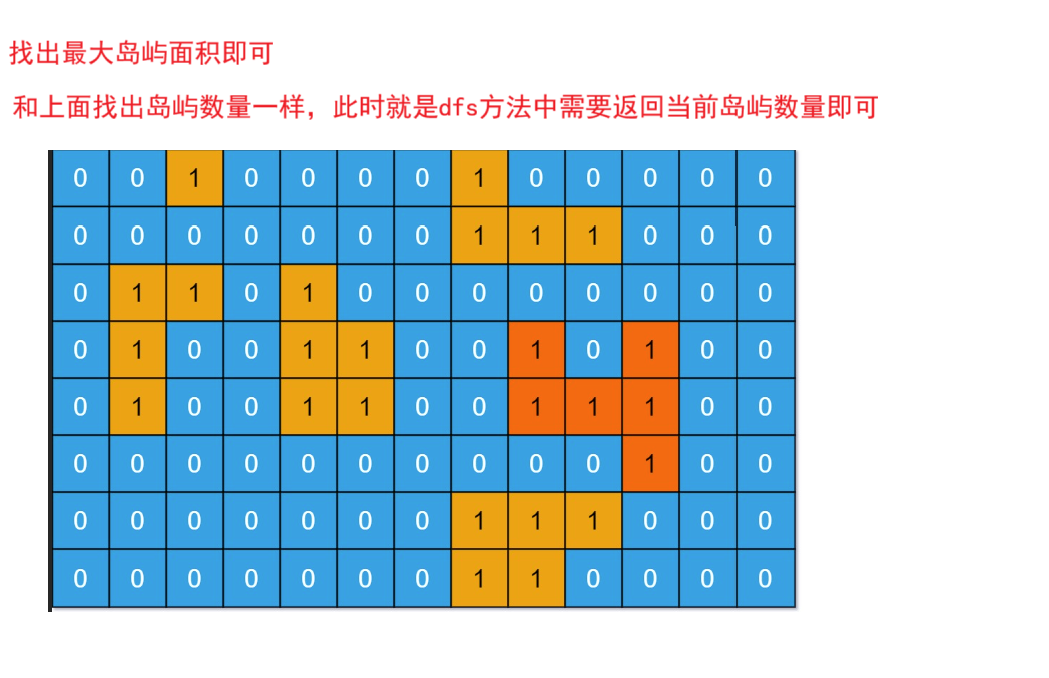
题目解析 :就是找出岛屿最大面积
思想:此时和上一题岛屿数量类似,此时我们只需要在dfs方法中返回此时岛屿数量即可
java
class Solution {
int[] dx = { 0, 0, 1, -1 };
int[] dy = { 1, -1, 0, 0 };
boolean[][] visited;//标记已经遍历过的
int m = 0;
int n = 0;
public int maxAreaOfIsland(int[][] grid) {
int ret = 0;
m = grid.length;
n = grid[0].length;
visited = new boolean[m][n];
//此时遍历这个岛屿的时候统计一下它的面积,返回
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1 && visited[i][j] == false) {
//此时更新结果
ret = Math.max(ret, dfs(grid, i, j));
}
}
}
return ret;
}
public int dfs(int[][] grid,int i,int j){
int count = 0;//此时岛屿面积
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{i,j});
visited[i][j] = true;
count++;
while(!queue.isEmpty()){
//队列为空就结束
int[] tem = queue.poll();
int a = tem[0];
int b = tem[1];
for(int k = 0;k<4;k++){
int x = a + dx[k];
int y = b + dy[k];
//延申
if(x >= 0&&x < m && y >= 0 && y < n &&grid[x][y] == 1 && visited[x][y] == false){
queue.add(new int[]{x,y});
visited[x][y] = true;
count++;
}
}
}
return count;
}
}被围住的区域

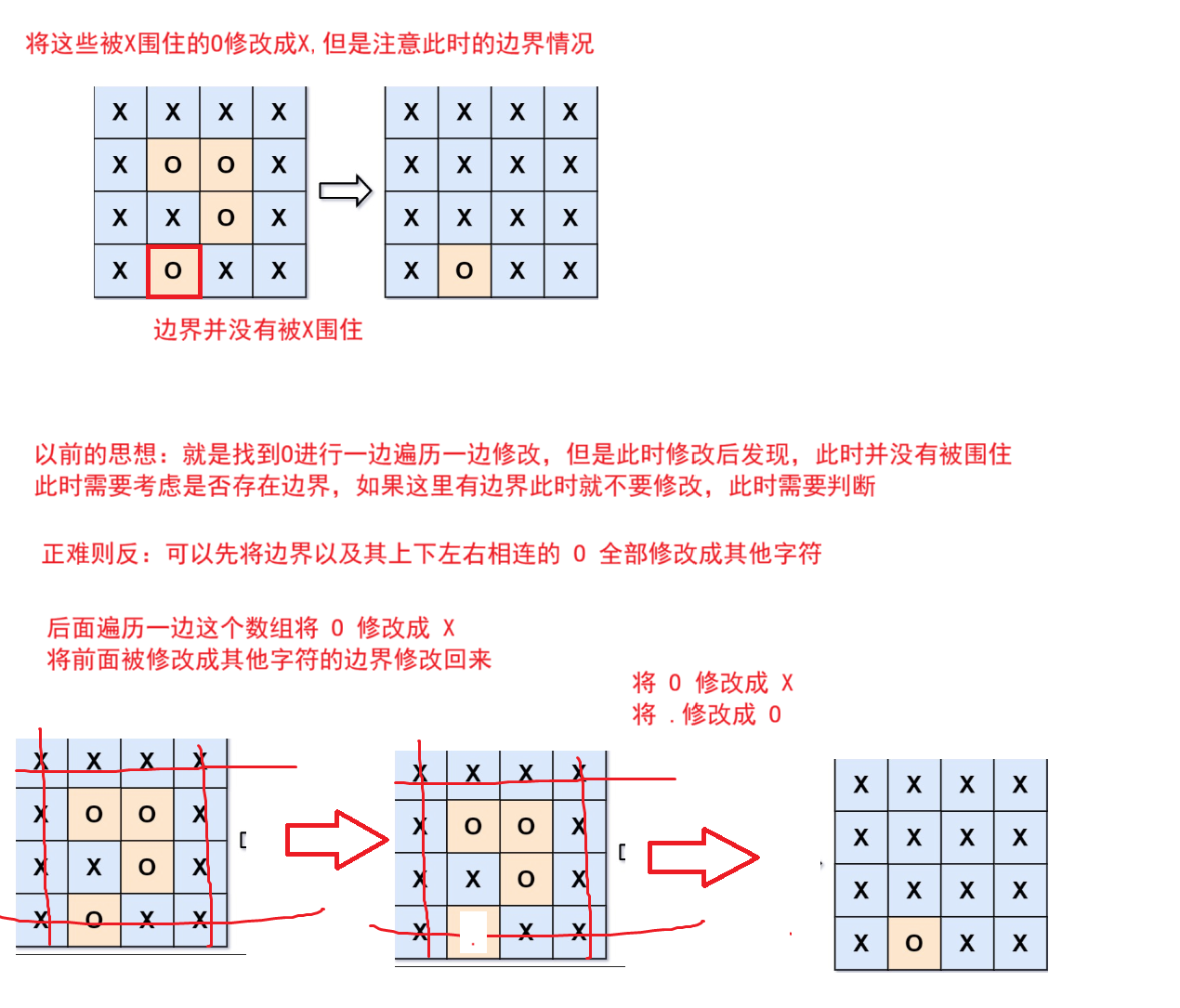
题目解析 :就是将被X围住的O修改成X,未被围住的不做修改
思想:由于以前是一边遍历,一边修,但是这里会出现不需要修改的问题,可能修改一半发现不需要修改,此时这里还需要进行二次判断因此这里采用正难则反的思想
1.先使用dfs遍历边界,此时将边界及其扩展部分修改成 其他字符
2.最后遍历一遍数组,将剩下未被修改的O修改成X,将这里被修改成其他字符的修改回以前的O字符
java
class Solution {
int[] dx = { 0, 0, 1, -1 };
int[] dy = { 1, -1, 0, 0 };
int m = 0;
int n = 0;
public void solve(char[][] board) {
m = board.length;
n = board[0].length;
//1.将边界的O以及相邻的O全部修改成 . 最后在修改回来
//左右两列
for (int i = 0; i < m; i++) {
if (board[i][0] == 'O') {
dfs(board, i, 0);
}
if (board[i][n - 1] == 'O') {
dfs(board, i, n - 1);
}
}
//上下两行
for (int i = 0; i < n; i++) {
if (board[0][i] == 'O') {
dfs(board, 0, i);
}
if (board[m - 1][i] == 'O') {
dfs(board, m - 1, i);
}
}
//剩下的O修改成X,将上面修改的还原
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == 'O') {
board[i][j] = 'X';
//修改回来
} else if (board[i][j] == '.') {
board[i][j] = 'O';
}
}
}
}
public void dfs(char[][] board, int i, int j) {
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[] { i, j });
board[i][j] = '.';//修改成.
while (!queue.isEmpty()) {
int[] tem = queue.poll();
int a = tem[0];
int b = tem[1];
for (int k = 0; k < 4; k++) {
int x = a + dx[k];
int y = b + dy[k];
if (x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O') {
queue.add(new int[] { x, y });
board[x][y] = '.';
}
}
}
}
}