一、树
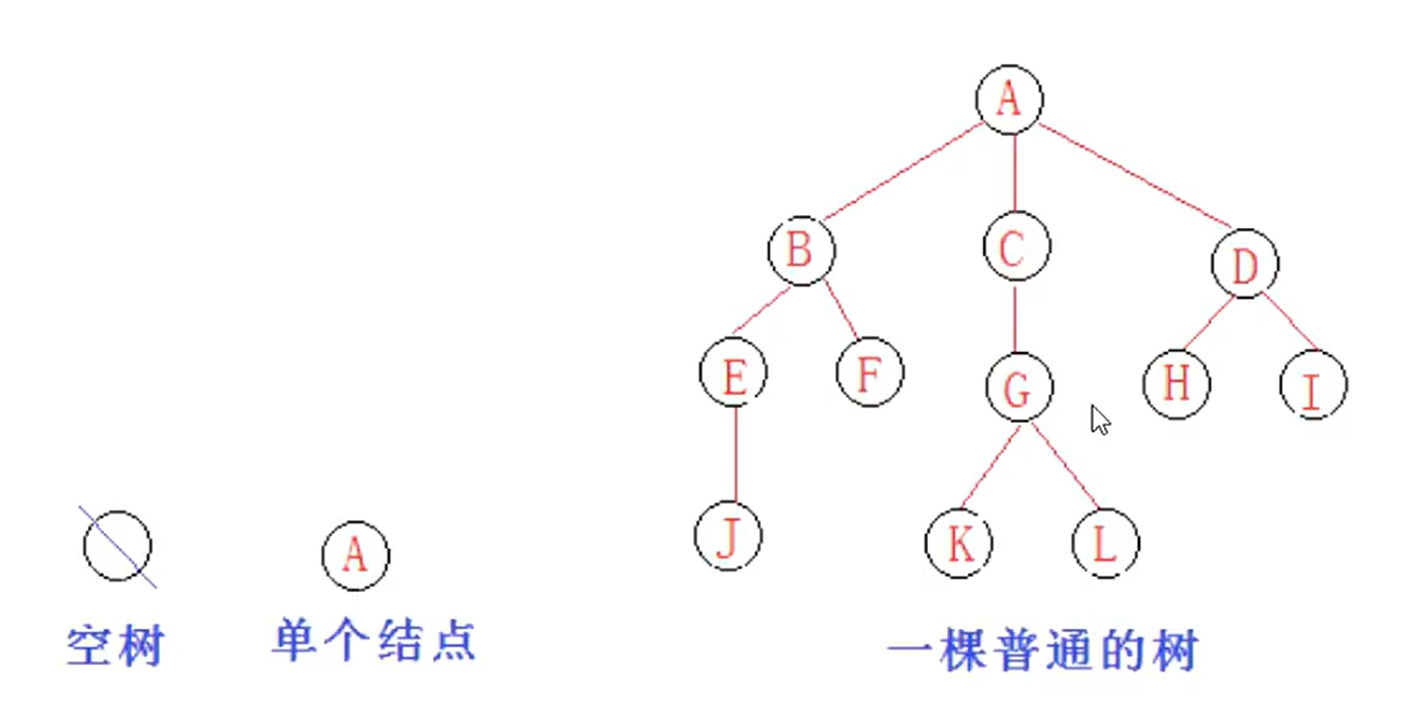
1.常见概念
节点的度: 一个节点含有的子树的个数称为该节点的度;如上图:A的为6
叶节点或终端节点: 度为0的节点称为叶节点;如上图:B、C、H、I.等节点为叶节点
非终端节点或分支节点:度不为0的节点;如上图:D、E、F、G.等节点为分支节点
双亲节点或父节点: 若一个节点含有子节点,则这个节点称为其子节点的父节点;如上图:A是B的父节点
孩子节点或子节点: 一个节点含有的子树的根节点称为该节点的子节点;如上图:B是A的孩子节点
兄弟节点:(亲兄弟) 具有相同父节点的节点互称为兄弟节点;如上图:B、C是兄弟节点
树的度: 一棵树中,最大的节点的度称为树的度;如上图:树的度为6
节点的层次: 从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
树的高度或深度: 树中节点的最大层次;如上图:树的高度为4(空树的高度为0)
节点的祖先: 从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙: 以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
**森林:**由m(m>0)棵互不相交的多颗树的集合称为森林;(数据结构中的学习并查集本质就是一个森林)
2.树的表示
①顺序表存孩子的指针
cpp
struct TreeNode
{
int data;
vector <struct TreeNode*> childs;
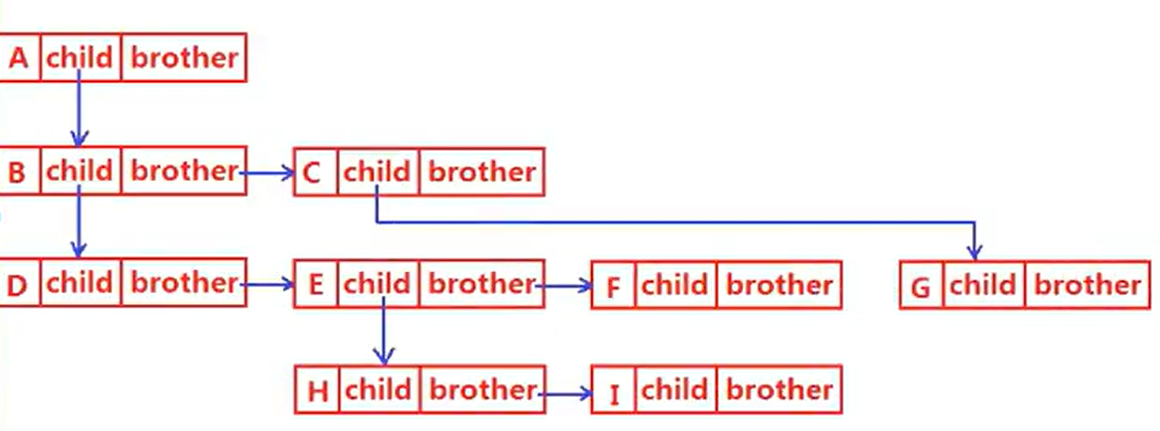
};②左孩子右兄弟
cpp
typedef int DataType;
struct Node
{
struct Node* _firstChild1;
//第一个孩子节点
struct Node* _pNextBrother;
//指向其下一个兄弟节点
DataType _data;
//节点中的数据域
};
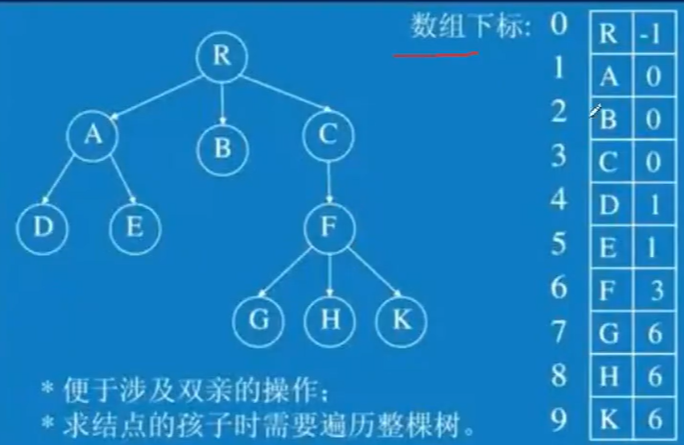
③双亲表示法
用数组存父节点的下标
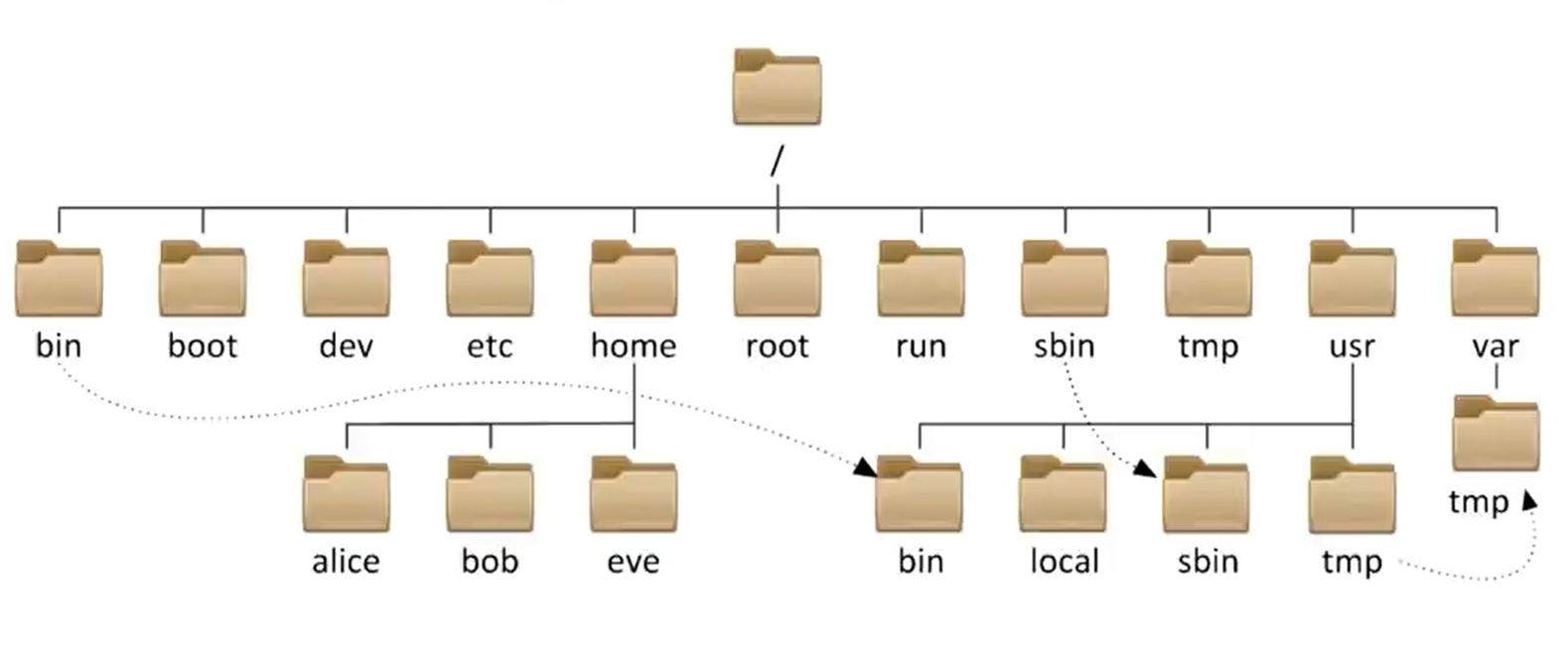
3.树在实际中的运用
表示文件系统的目录树结构
二、二叉树基础
1.概念
一棵二叉树是结点的一个有限集合,该集合或者为空,或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
2.特点
①每个结点最多有两棵子树,即二叉树不存在度大于2的结点。
②二叉树的子树有左右之分,其子树的次序不能颠倒。
3.任何一颗二叉树都有三个部分
①根节点
②左子树
③右子树
**分治算法:**分而治之,大问题分成类似子问题,子问题再分成子问题......直到子问题不可再分割
前序(先根遍历):根、左子树、右子树(根在前面)
A B D E C
A B D NULL NULL E NULL NULL C NULL NULL
中序(中根遍历):左子树、根、右子树(根在中间)
D B E A C
NULL D NULL B NULL E NULL A NULL C NULL
后序(后根遍历):左子树、右子树、根
4.二叉树的创建
cpp
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
typedef char BTDataType;
typedef struct BinaryTreeNode
{
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
BTDataType data;
}BTNode;5.前序遍历
cpp
void PrevOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
//前中后序只需调整这三行代码
printf("%c ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}6.手动创建二叉树
cpp
void Test()
{
BTNode* A = (BTNode*)malloc(sizeof(BTNode));
A->data = 'A';
A->left = NULL;
A->right = NULL;
BTNode* B = (BTNode*)malloc(sizeof(BTNode));
B->data = 'B';
B->left = NULL;
B->right = NULL;
BTNode* C = (BTNode*)malloc(sizeof(BTNode));
C->data = 'C';
C->left = NULL;
C->right = NULL;
BTNode* D = (BTNode*)malloc(sizeof(BTNode));
D->data = 'D';
D->left = NULL;
D->right = NULL;
BTNode* E = (BTNode*)malloc(sizeof(BTNode));
E->data = 'E';
E->left = NULL;
E->right = NULL;
A->left = B;
A->right = C;
B->left = D;
B->right = E;
PrevOrder(A);
printf("\n");
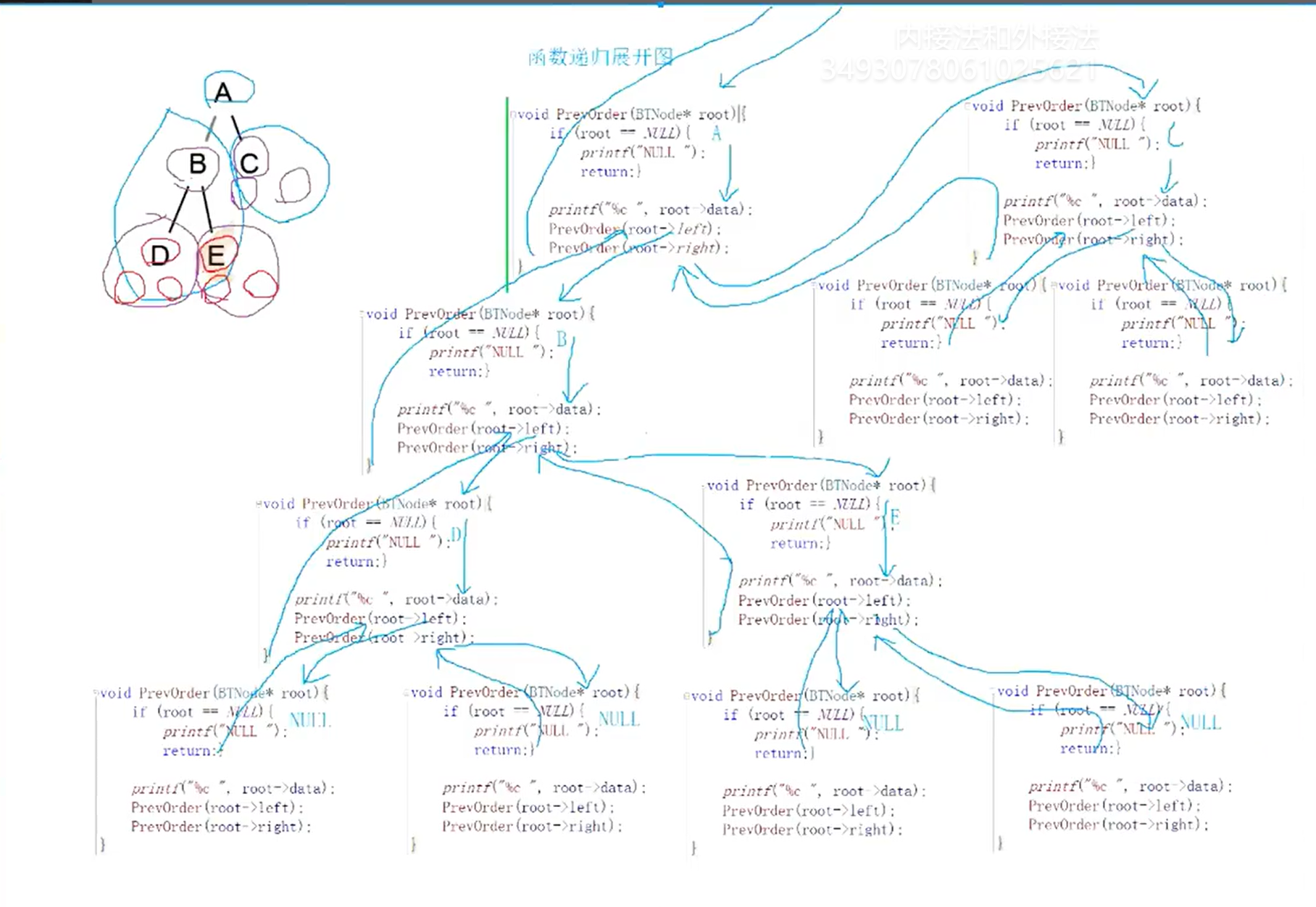
}7.画函数递归图
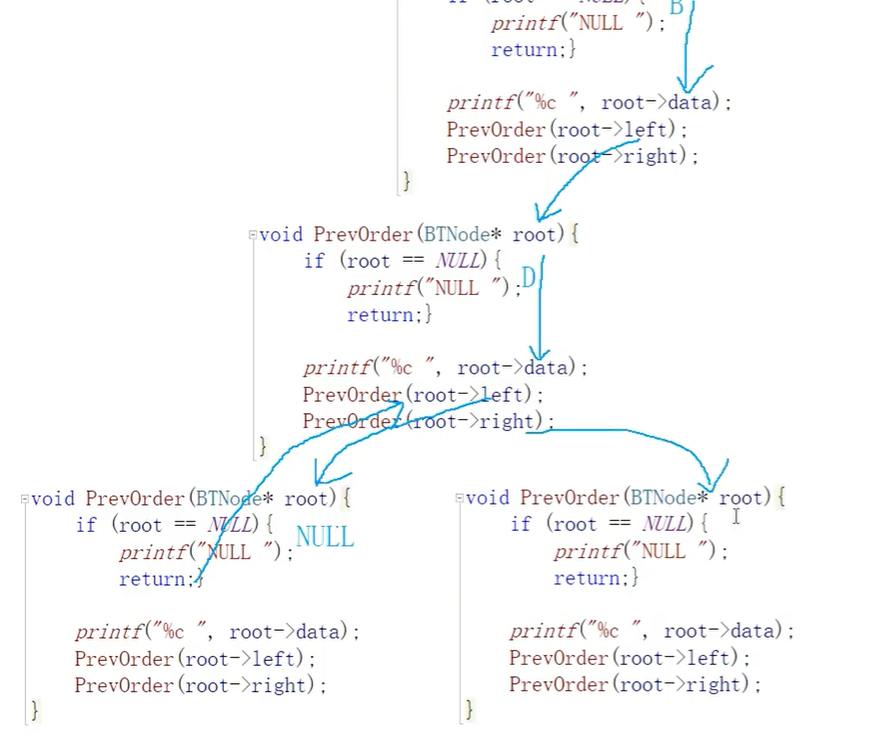
8.特殊的二叉树:
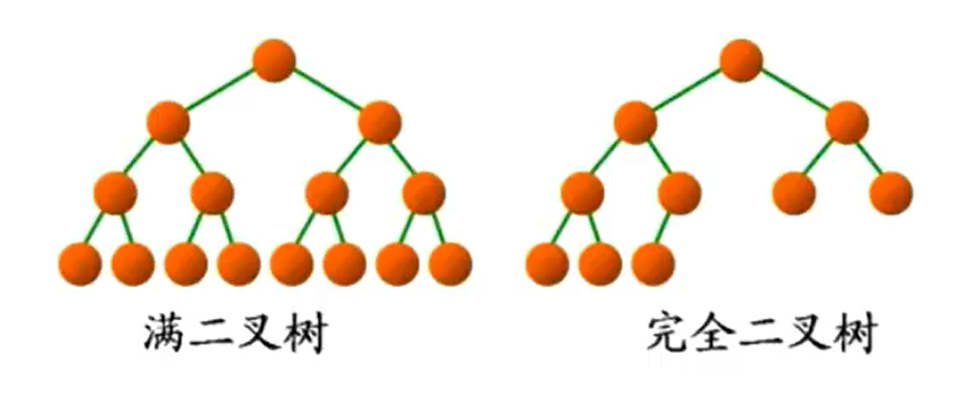
①满二叉树: 一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为h,且结点总数N=(2^h)-1,则它就是满二叉树。h=log2(N)+1
**②完全二叉树:**完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引|出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一---对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。
判定完全二叉树:
假设树的高度是h
1、前h-1层都是满的
2、最后一层不满,但是最后一层从左往右都是连续的
9. 二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
二叉树的性质
1.若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1) 个结点
2.若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-1 .
3.对任何一棵二叉树,如果度为0其叶结点个数为n0,度为2的分支结点个数为n2,则有n0=n2+1
4.若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=LogN
普通二叉树,不讲普通二叉树的增删查改,在实际中普通二叉树增删查改没有意义
a.可以为后面学习复杂有用平衡树做铺垫
b.考试角度,很多题都是出在普通二又树上的
真正有用的是搜索二叉树,任何一颗树,左子树都比根要小,右子树都比根要大a.搜索中查找一个数,最多查找高度次,时间复杂度:0(N)
b.左右两边的节点数据比较均匀:平衡树、AVL树、红黑树、B树------多叉搜索树(数据库原理)
5.例题
例1:在具有2n个结点的完全二叉树中,叶子结点个数为(n)
假设度为0的节点有X0个,度为1的节点有X1个,度为2的节点有X2个
X0 + X1 + X2=2n
其中,X0= X2+1
X0 + X1 + X0-1 =2n
2X0+X1 -1=2n
X1可能是1,也可能是0
在这棵树里面,X1是1
例2:一棵完全二叉树的节点数位为531个,那么这棵树的高度为(10)
假设这棵树的高度是h,假设最后一层缺了X个
2h-1-X=531
X的范围[0,2^(h-1)-1]
常识:2^10=1024
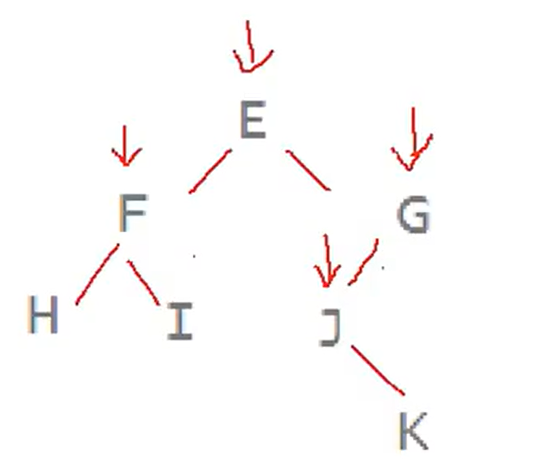
例3:先序遍历:EFHIGJK;中序遍历:HFIEJKG。请还原该二叉树:
先通过先序确定根,再分割出左右子树中序区间
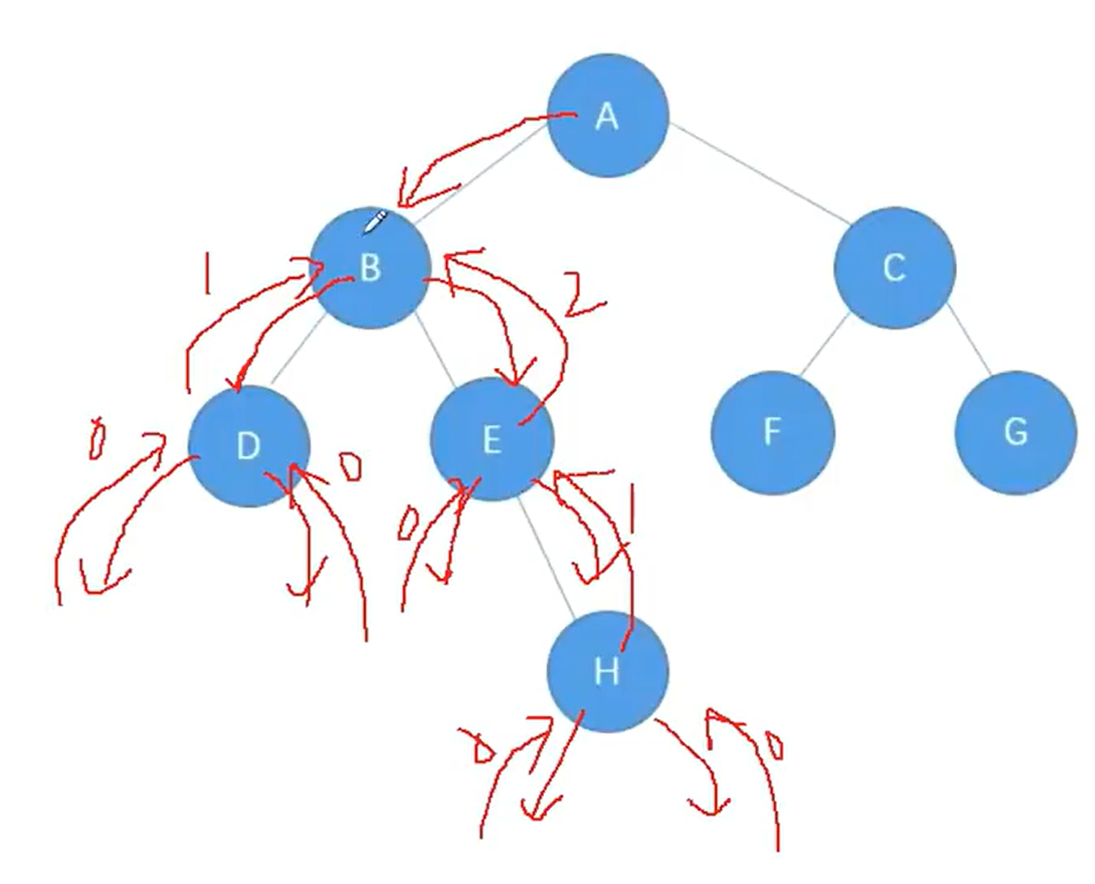
10.求二叉树的节点个数
左边+右边+根
cpp
int TreeSize(BTNode* root)
{
if (root == NULL)
return 0;
else
return TreeSize(root->left) + TreeSize(root->right) + 1;
}递归图如下:
11.求二叉树叶子节点的个数
cpp
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
return 0;
if (root->left == NULL && root->right == NULL)
return 1;
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}递归图如下:
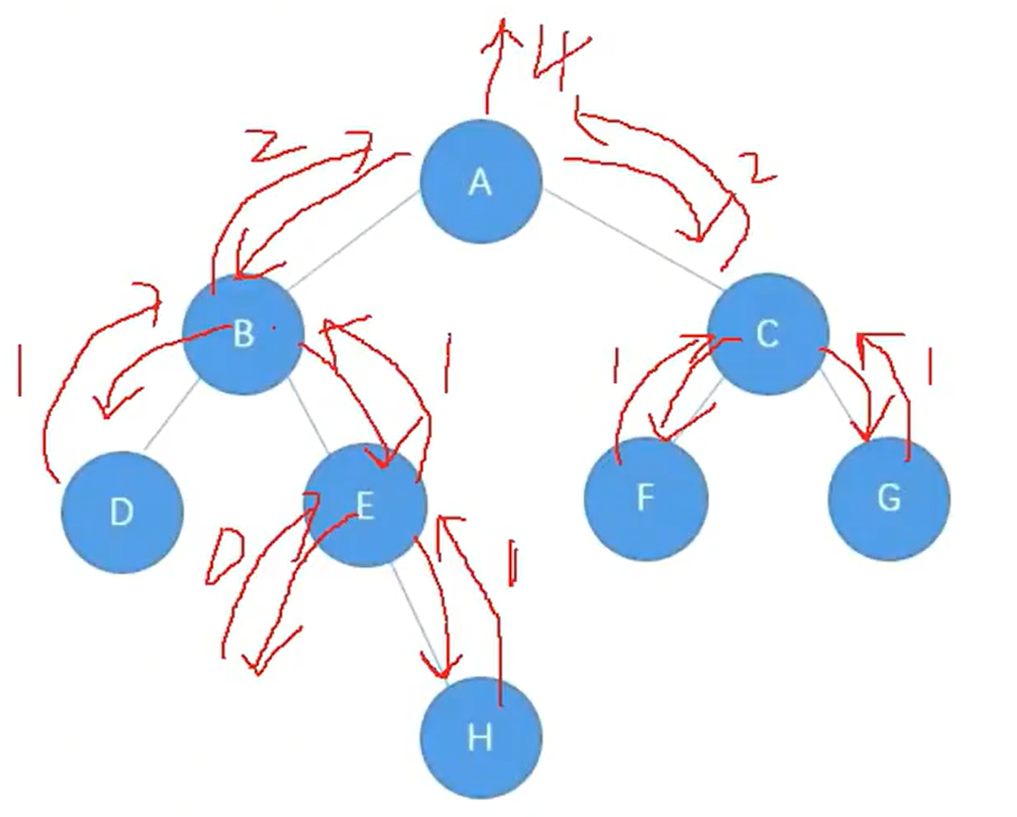

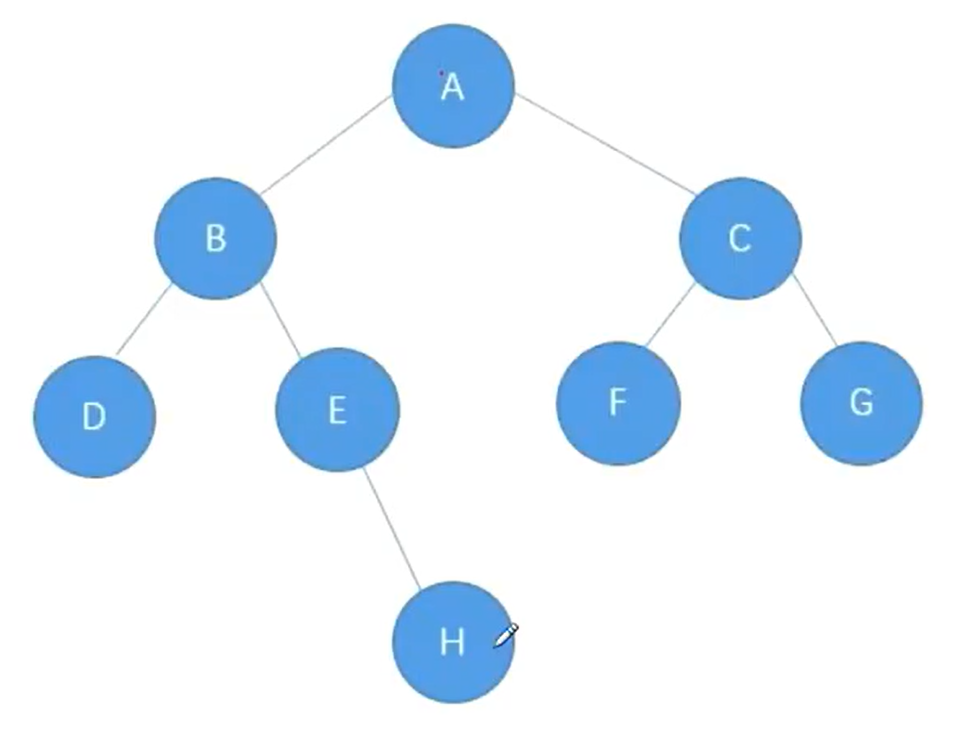
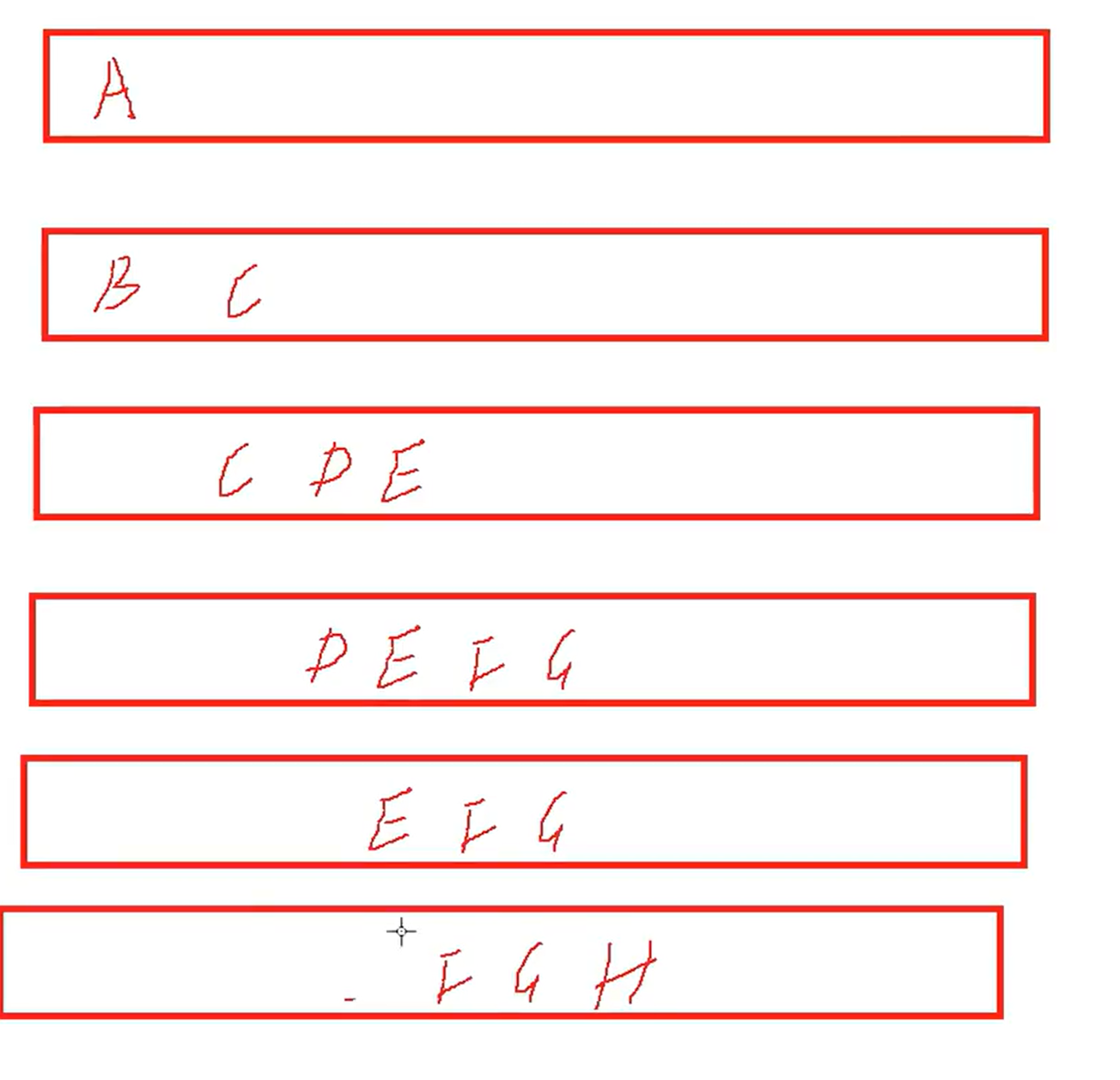
12.二叉树的层序遍历

cpp
void levelOrder(struct TreeNode* root, int* returnSize, int** returnColumnSizes)
{
Queue q;
Init(&q);
//如果root不为空,就把root入到队列中
if (root)
Push(&q,root);
//如果队列不为空
while (!isEmpty(&q))
{
//把root取出来
TreeNode* front = Top(&q);
//把节点的指针从队列中删除,节点还在
Pop(&q);
printf("%c ", front->val);
//如果root的左孩子不为空
if (front->left)
{
//把左孩子放入队列中
Push(&q, root->left);
}
if (front->right)
{
Push(&q, root->right);
}
}
printf("\n");
}