区间 dp
区间 dp 也是线性 dp 的⼀种,它⽤区间的左右端点来描述状态,通过⼩区间的解来推导出⼤区间的 解。因此,区间 DP 的核⼼思想是 将⼤区间划分为⼩区间 ,它的状态转移⽅程通常依赖于区间的划分 点。
常⽤的划分点的⽅式有两个:
• 基于区间的左右端点,分情况讨论;
• 基于区间上某⼀点,划分成左右区间讨论。
1 回⽂字串
题⽬来源: 洛⾕
题⽬链接: P1435 [IOI2000] 回⽂字串
难度系数: ★★
题目背景
IOI2000 第一题
题目描述
回文词是一种对称的字符串。任意给定一个字符串,通过插入若干字符,都可以变成回文词。此题的任务是,求出将给定字符串变成回文词所需要插入的最少字符数。
比如 Ab3bd 插入 2 个字符后可以变成回文词 dAb3bAd 或 Adb3bdA,但是插入少于 2 个的字符无法变成回文词。
注意:此问题区分大小写。
输入格式
输入共一行,一个字符串。
输出格式
有且只有一个整数,即最少插入字符数。
输入输出样例
输入 #1复制
Ab3bd输出 #1复制
2说明/提示
数据范围及约定
记字符串长度为 l。
对于全部数据,0<l≤1000。
【解法】


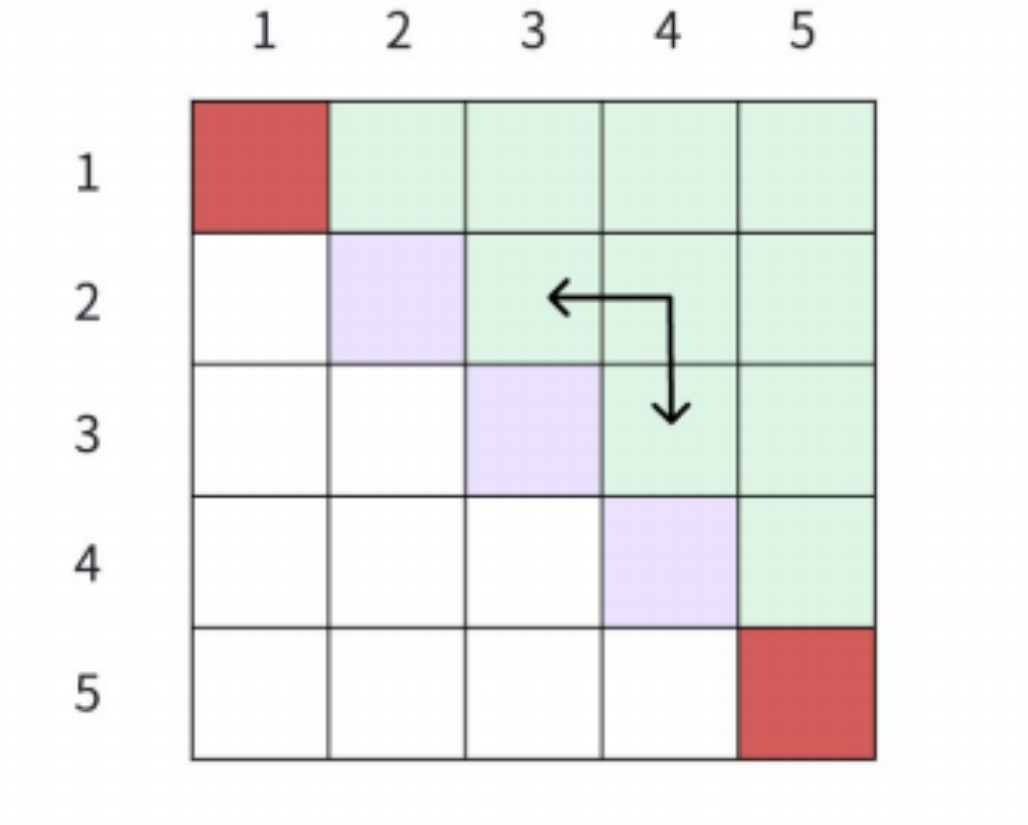

【参考代码】
cpp
#include <iostream>
using namespace std;
const int N = 1010; // 定义数组最大长度,因为字符串最长1000,留10个余量
int f[N][N]; // f[i][j]存区间[i,j]变回文的最少插入数,默认初始值0
int main()
{
string s; cin >> s; // 输入字符串,比如输入Ab3bd
int n = s.size(); // n是字符串长度,Ab3bd的n=5
s = " " + s; // 给字符串前面加个空字符,变成:" Ab3bd",编号1-5
// 第一步:枚举子串长度(len=1表示1个字符,len=5表示整个字符串)
for(int len = 1; len <= n; len++)
{
// 第二步:枚举左端点i,保证i+len-1 <=n(右端点不超界)
for(int i = 1; i + len - 1 <= n; i++)
{
int j = i + len - 1; // 计算右端点j:左端点+长度-1(比如i=1,len=5→j=5)
// 情况1:i和j是同一个字符(子串长度1),本身是回文,插0个
// 情况2:i和j字符相同,直接取中间子串的结果
if(s[i] == s[j])
f[i][j] = f[i + 1][j - 1];
// 情况3:i和j字符不同,选补左边或补右边的最小值,再加1
else
f[i][j] = min(f[i + 1][j], f[i][j - 1]) + 1;
}
}
cout << f[1][n] << endl; // 输出整个字符串(1到n)的最少插入数
return 0;
}2 Treats for the Cows
题⽬来源: 洛⾕
题⽬链接: P2858 [USACO06FEB] Treats for the Cows G/S
难度系数: ★★
题目描述
约翰经常给产奶量高的奶牛发特殊津贴,于是很快奶牛们拥有了大笔不知该怎么花的钱。为此,约翰购置了 N(1≤N≤2000) 份美味的零食来卖给奶牛们。每天约翰售出一份零食。当然约翰希望这些零食全部售出后能得到最大的收益,这些零食有以下这些有趣的特性:
- 零食按照 1,...,N 编号,它们被排成一列放在一个很长的盒子里。盒子的两端都有开口,约翰每天可以从盒子的任一端取出最外面的一个。
- 与美酒与好吃的奶酪相似,这些零食储存得越久就越好吃。当然,这样约翰就可以把它们卖出更高的价钱。
- 每份零食的初始价值不一定相同。约翰进货时,第 i 份零食的初始价值为 Vi(1≤V≤1000)。
- 第 i 份零食如果在被买进后的第 a 天出售,则它的售价是 Vi×a。
Vi 的是从盒子顶端往下的第 i 份零食的初始价值。约翰告诉了你所有零食的初始价值,并希望你能帮他计算一下,在这些零食全被卖出后,他最多能得到多少钱。
输入格式
第一行一个正整数 N。
接下来 2∼N+1 行,第 i+1 行为一个正整数 Vi。
输出格式
一行一个整数表示答案。
输入输出样例
输入 #1复制
5
1
3
1
5
2输出 #1复制
43说明/提示
样例的最优解是:按 1→5→2→3→4 的顺序卖零食,得到的钱数是 1×1+2×2+3×3+4×1+5×5=43。
【解法】

【参考代码】
cpp
#include <iostream>
using namespace std;
const int N = 2010; // 零食最多2000个,留10个余量
int n; // 零食总数
int a[N]; // a[i]存第i个零食的初始价值
int f[N][N]; // f[i][j]存区间[i,j]卖完的最大收益,默认初始值0
int main()
{
cin >> n; // 输入零食总数,比如示例输入5
// 输入每个零食的初始价值,编号1~n
for(int i = 1; i <= n; i++) cin >> a[i];
// 第一步:枚举区间长度(len=1表示1个零食,len=5表示整个区间)
for(int len = 1; len <= n; len++)
{
// 第二步:枚举左端点i,保证右端点j=i+len-1不超过n
for(int i = 1; i + len - 1 <= n; i++)
{
int j = i + len - 1; // 计算右端点j:左端点+长度-1
int cnt = n - len + 1;// 算"先拿的这个零食"的售卖天数
// 两种卖法选最大值:
// 1. 先拿左边i,收益=a[i]*cnt + 剩下[i+1,j]的最大收益
// 2. 先拿右边j,收益=a[j]*cnt + 剩下[i,j-1]的最大收益
f[i][j] = max(f[i + 1][j] + a[i] * cnt, f[i][j - 1] + a[j] * cnt);
}
}
cout << f[1][n] << endl; // 输出整个区间[1,n]的最大收益
return 0;
}3 ⽯⼦合并(弱化版)
题⽬来源: 洛⾕
题⽬链接: P1775 ⽯⼦合并(弱化版)
难度系数: ★★
题目描述
设有 N(N≤300) 堆石子排成一排,其编号为 1,2,3,⋯,N。每堆石子有一定的质量 mi (mi≤1000)。现在要将这 N 堆石子合并成为一堆。每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻。合并时由于选择的顺序不同,合并的总代价也不相同。试找出一种合理的方法,使总的代价最小,并输出最小代价。
输入格式
第一行,一个整数 N。
第二行,N 个整数 mi。
输出格式
输出文件仅一个整数,也就是最小代价。
输入输出样例
输入 #1复制
4
2 5 3 1输出 #1复制
22【解法】

【参考代码】
cpp
#include <iostream>
#include <cstring> // 用memset函数需要的头文件
using namespace std;
const int N = 310; // 石子最多300堆,留10个余量
int n; // 石子堆数
int f[N][N]; // f[i][j]存合并[i,j]石子的最小代价
int sum[N]; // 前缀和数组,sum[i]是前i堆石子总质量
int main()
{
cin >> n; // 输入石子堆数,示例输入4
for(int i = 1; i <= n; i++)
{
int x; cin >> x; // 输入每堆石子质量,示例:2、5、3、1
sum[i] = sum[i - 1] + x; // 计算前缀和,sum[0]=0(默认)
}
// 初始化:把f数组全部设为极大值(0x3f是十六进制,对应十进制1061109567)
memset(f, 0x3f, sizeof f);
// 区间长度为1时,不用合并,代价为0
for(int i = 0; i <= n; i++) f[i][i] = 0;
// 第一步:枚举区间长度(len=2开始,因为len=1已初始化)
for(int len = 2; len <= n; len++)
{
// 第二步:枚举左端点i,保证右端点j=i+len-1不超过n
for(int i = 1; i + len - 1 <= n; i++)
{
int j = i + len - 1; // 计算右端点j
int t = sum[j] - sum[i - 1]; // 算[i,j]石子总质量(最后一步合并的代价)
// 第三步:枚举分割点k(从i到j-1)
for(int k = i; k < j; k++)
{
// 核心:选所有分割方式中代价最小的
// f[i][k]:合并[i,k]的最小代价;f[k+1][j]:合并[k+1,j]的最小代价;t:最后一步合并的代价
f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + t);
}
}
}
cout << f[1][n] << endl; // 输出合并[1,n]的最小代价
return 0;
}4 ⽯⼦合并
题⽬来源: 洛⾕
题⽬链接: P1880 [NOI1995] ⽯⼦合并
难度系数: ★★★
题目描述
在一个圆形操场的四周摆放 N 堆石子,现要将石子有次序地合并成一堆,规定每次只能选相邻的 2 堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。
试设计出一个算法,计算出将 N 堆石子合并成 1 堆的最小得分和最大得分。
输入格式
数据的第 1 行是正整数 N,表示有 N 堆石子。
第 2 行有 N 个整数,第 i 个整数 ai 表示第 i 堆石子的个数。
输出格式
输出共 2 行,第 1 行为最小得分,第 2 行为最大得分。
输入输出样例
输入 #1复制
4
4 5 9 4输出 #1复制
43
54说明/提示
1≤N≤100,0≤ai≤20。
【解法】
处理环形问题的技巧: 倍增 。
在数组后⾯,将原始数组复写⼀遍 ,然后在倍增之后的数组上做⼀次⽯⼦合并(弱化版),就能得到 以所有位置为起点并且⻓度为 len 的最⼩合并代价。
【参考代码】
cpp
#include <iostream>
#include <cstring> // memset函数需要的头文件
using namespace std;
const int N = 210; // 最多100堆,倍增后200,留10个余量
int n, m; // n:原始堆数;m:倍增后数组长度(n+n)
int s[N]; // 前缀和数组(先存原始石子数,再算前缀和)
int f[N][N]; // 存[i,j]合并的最小得分
int g[N][N]; // 存[i,j]合并的最大得分
int main()
{
cin >> n; // 输入原始堆数,示例n=4
for(int i = 1; i <= n; i++)
{
cin >> s[i]; // 输入每堆石子数,示例:4、5、9、4
s[i + n] = s[i]; // 倍增:复制到n+1~2n位置,s[5]=4,s[6]=5,s[7]=9,s[8]=4
}
m = n + n; // 倍增后数组长度,m=8
// 计算前缀和:s[i] = 前i堆石子的总数量
for(int i = 1; i <= m; i++)
{
s[i] += s[i - 1]; // 比如s[1]=4, s[2]=4+5=9, s[3]=18, s[4]=22, s[5]=26...
}
// 初始化:f数组设为极大值(找最小值),g数组设为极小值(找最大值)
memset(f, 0x3f, sizeof f); // 0x3f是极大值(约1e9)
memset(g, -0x3f, sizeof g); // -0x3f是极小值(约-1e9)
// 单个石子堆不用合并,得分0
for(int i = 1; i <= m; i++)
{
f[i][i] = g[i][i] = 0;
}
// 第一步:枚举区间长度(len=1到n,因为我们只需要合并n堆)
for(int len = 1; len <= n; len++)
{
// 第二步:枚举左端点i,保证右端点j=i+len-1 ≤ m
for(int i = 1; i + len - 1 <= m; i++)
{
int j = i + len - 1; // 计算右端点j
int t = s[j] - s[i - 1]; // [i,j]总数量(最后一步合并的得分)
// 第三步:枚举分割点k(从i到j-1)
for(int k = i; k < j; k++)
{
// 最小得分:选所有分割方式中最小的
f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + t);
// 最大得分:选所有分割方式中最大的
g[i][j] = max(g[i][j], g[i][k] + g[k + 1][j] + t);
}
}
}
// 第四步:找所有起点的最小/最大得分
int ret1 = 0x3f3f3f3f; // 最小得分初始为极大值
int ret2 = -0x3f3f3f3f;// 最大得分初始为极小值
for(int i = 1; i <= n; i++)
{
// 以i为起点,合并n堆:区间[i, i+n-1]
ret1 = min(ret1, f[i][i + n - 1]);
ret2 = max(ret2, g[i][i + n - 1]);
}
// 输出结果
cout << ret1 << endl << ret2 << endl;
return 0;
}5. 248
题⽬来源: 洛⾕
题⽬链接: P3146 [USACO16OPEN] 248 G
难度系数: ★★★
题目描述
贝西喜欢在手机上下载游戏来玩,尽管她确实觉得对于自己巨大的蹄子来说,小小的触摸屏用起来相当笨拙。
她对当前正在玩的这个游戏特别感兴趣。游戏开始时给定一个包含 N 个正整数的序列(2≤N≤248),每个数的范围在 1...40 之间。在一次操作中,贝西可以选择两个相邻且相等的数,将它们替换为一个比原数大 1 的数(例如,她可以将两个相邻的 7 替换为一个 8)。游戏的目标是最大化最终序列中的最大数值。请帮助贝西获得尽可能高的分数!
输入格式
第一行输入包含 N,接下来的 N 行给出游戏开始时序列的 N 个数字。
输出格式
请输出贝西能生成的最大整数。
显示翻译
题意翻译
输入输出样例
输入 #1复制
4
1
1
1
2输出 #1复制
3说明/提示
在示例中,贝西首先合并第二个和第三个 1,得到序列 1 2 2,然后将两个 2 合并为 3。注意,合并前两个 1 并不是最优策略。
【解法】

cpp
#include <iostream>
using namespace std;
const int N = 255; // 最多248个数,留7个余量
int n; // 序列长度
int a[N]; // 存原始序列的数
int f[N][N]; // f[i][j]:[i,j]合并成一个数的最大值(0表示合不成)
int main()
{
cin >> n; // 输入序列长度,示例n=4
int ret = 0; // 记录最终的最大数(初始0)
for(int i = 1; i <= n; i++)
{
cin >> a[i]; // 输入每个数,示例:1、1、1、2
f[i][i] = a[i]; // 单个数字,合并后就是自己,比如f[1][1]=1
ret = max(ret, a[i]); // 先更新ret为单个数字的最大值(示例初始ret=2)
}
// 第一步:枚举区间长度(从2开始,因为len=1已初始化)
for(int len = 2; len <= n; len++)
{
// 第二步:枚举左端点i,保证右端点j=i+len-1 ≤n
for(int i = 1; i + len - 1 <= n; i++)
{
int j = i + len - 1; // 计算右端点j
// 第三步:枚举分割点k(把[i,j]拆成[i,k]和[k+1,j])
for(int k = i; k < j; k++)
{
// 合并条件:① [i,k]和[k+1,j]都能合成一个数(f值≠0);② 合成的数相等
if(f[i][k] && f[i][k] == f[k + 1][j])
{
// 能合并:新数=原来的数+1,取最大值存到f[i][j]
f[i][j] = max(f[i][j], f[i][k] + 1);
}
}
// 更新全局最大值ret:当前区间[i,j]的f值可能是更大的数
ret = max(ret, f[i][j]);
}
}
cout << ret << endl; // 输出最大数
return 0;
}