图论最小生成树 MST问题

最小生成树

对于边带权无向图G=(V,E)G = (V,E)G=(V,E)，VVV中全部nnn个顶点和EEE中N−1N-1N−1条边构成的子图称为GGG的一棵生成树。在所有生成树中，边权和最小的称为最小生成树。

例如，对于下图，最小生成树为：

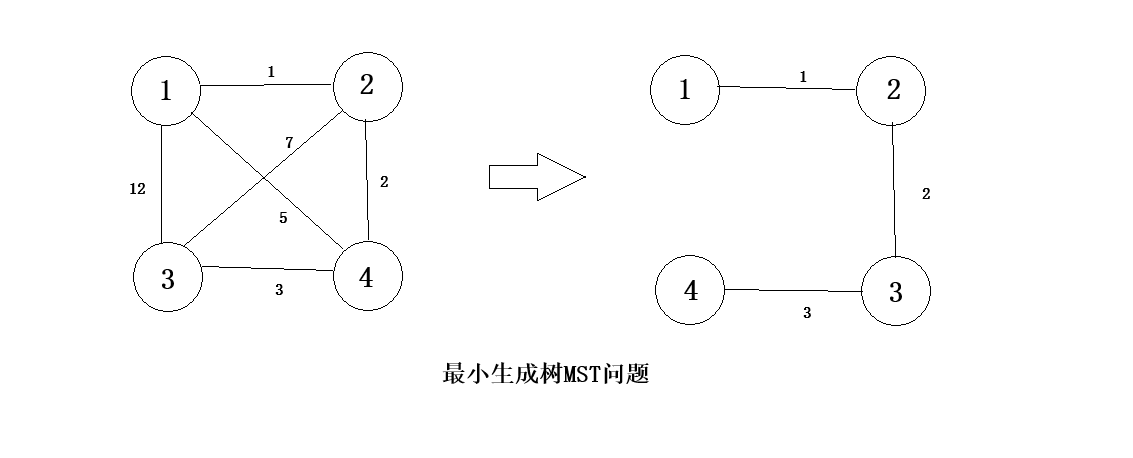
性质定理

定理：
对于任意一棵最小生成树，一定包含原无向图中权值最小的边。
证明：
反证：假设无向图G=(V,E)G = (V,E)G=(V,E)存在一棵最小生成树，不包含权值最小的边。
设E=(x,y,w)E = (x, y, w)E=(x,y,w)为权值最小边，如果把EEE加入树中，必然构成环，此时EEE的权值一定小于该环上其他几条边的中的任意一条。所以用EEE代替原有的边中的任意一条都必然为更优选择，故原树不是最小生成树，与假设矛盾。
故假设不成立，原命题成立。
证毕。

推论：

贪心思想在最小生成树问题中有重要应用。可以证明，在条件允许的情况下，始终优先选择使用最短的边。

Kruskal⁡\operatorname {Kruskal}Kruskal算法

原理

由上述贪心思想得来。其核心思想为，尽量选择合法的最短边 。

例如，对于下图的树而言：

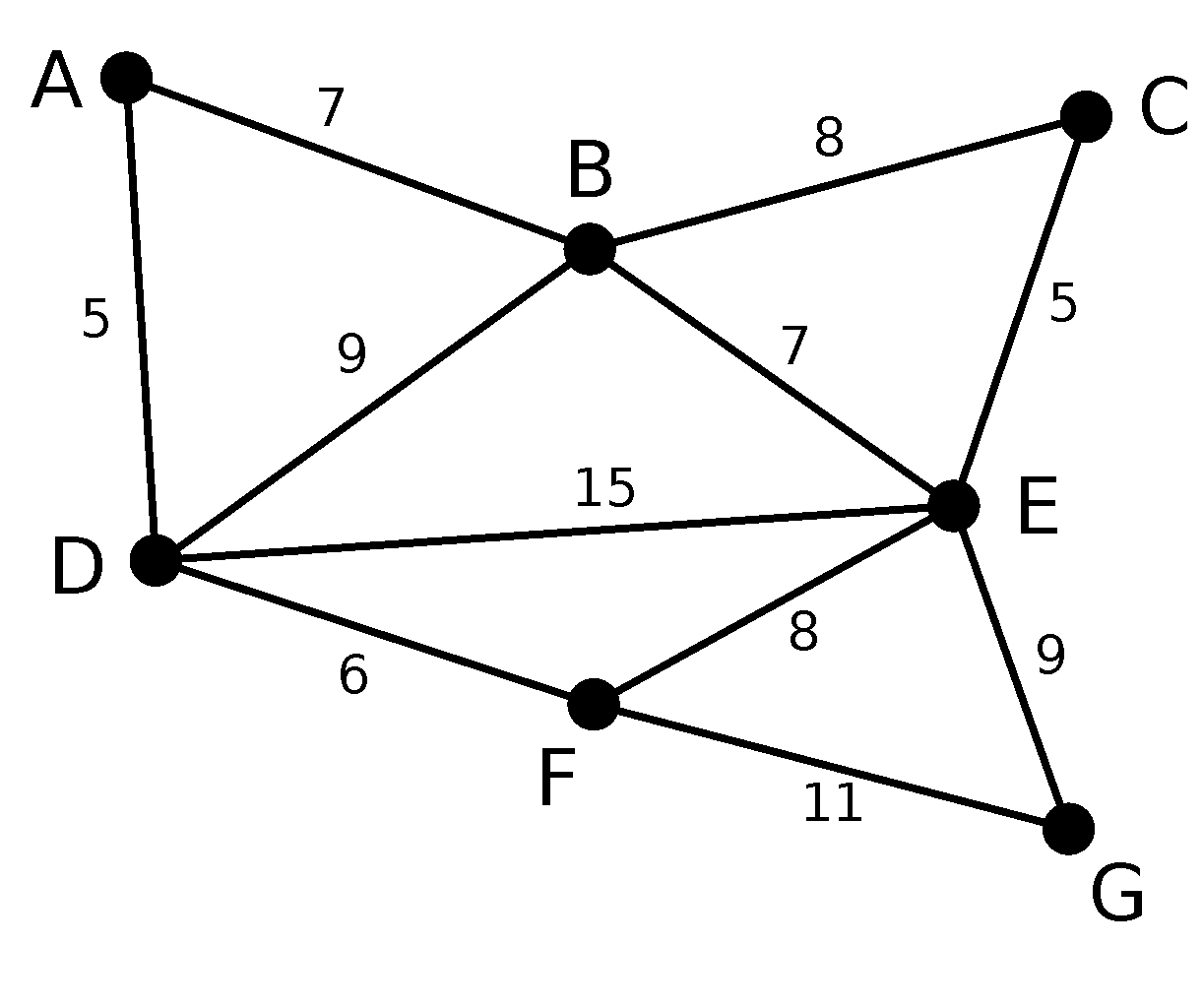
我们的选择顺序为：
AD⁡(5){\operatorname {AD}(5)}AD(5)
CE⁡(5){\operatorname {CE}(5)}CE(5)
DF⁡(6){\operatorname {DF}(6)}DF(6)
AB⁡(7){\operatorname {AB}(7)}AB(7)
BE⁡(7){\operatorname {BE}(7)}BE(7)
EG⁡(9){\operatorname {EG}(9)}EG(9)

实现

具体上，算法的实现如下：

利用并查集，一开始所有元素各成一个集合。
按照边权从小到大排序，按序扫描
若xxx与yyy已经同属一个集合，则说明这两点已经遍历过，再次遍历就会构成环，如下图。绿色为已经加入的边，{1,2,3}\{1,2,3\}{1,2,3}此时在同一集合内。如果连接红色边，构成环，不合法。所以此时忽略当前的边，继续访问下一个。
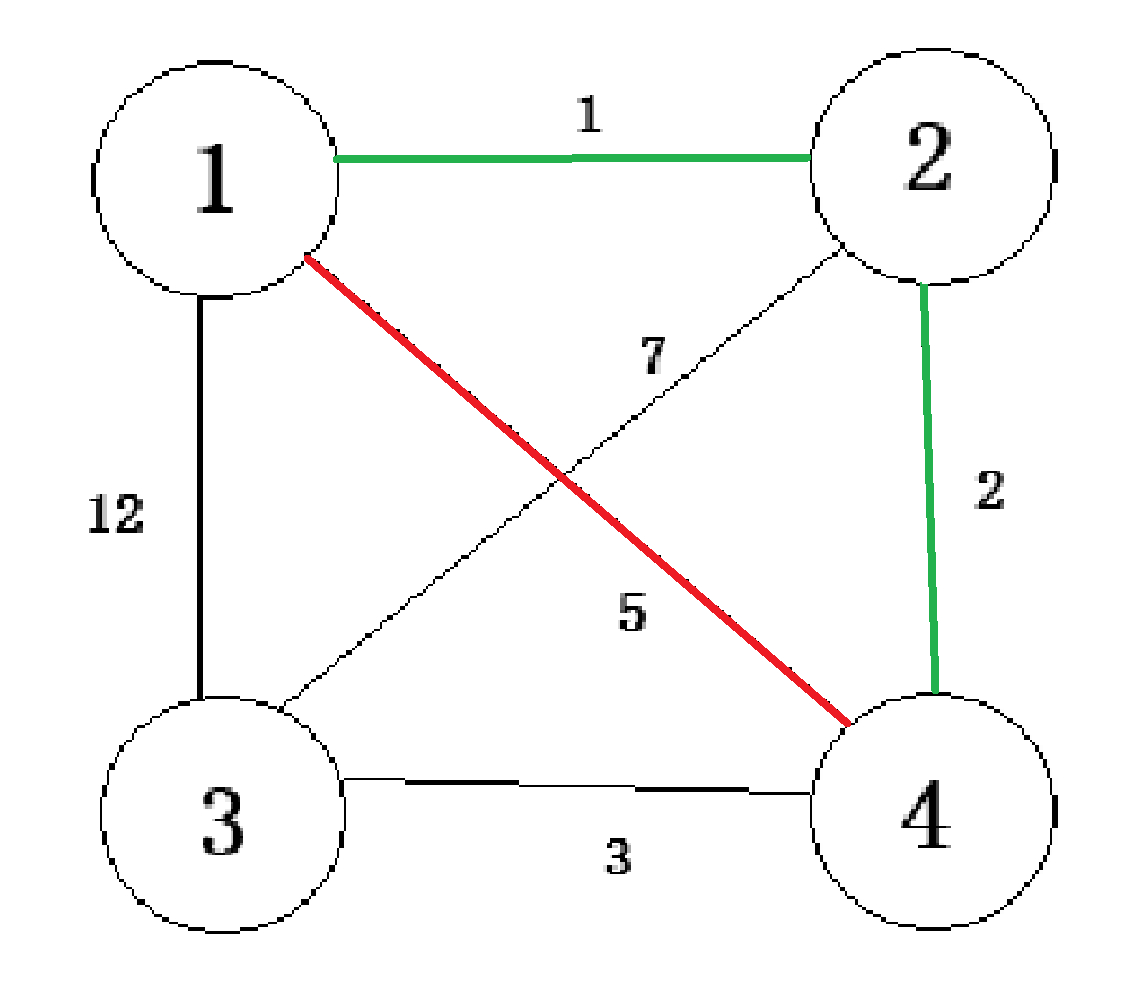
如果xxx与yyy不在同一集合，说明这两个点之间相连不构成环，可以连接。如下图，绿色为已经选择的边，蓝色为当前访问的边。此时{1,2}\{1, 2\}{1,2}在同一集合，{3}\{3\}{3}和{4}\{4\}{4}不在同一集合，所以可以合并。此时，我们将两并查集合并。
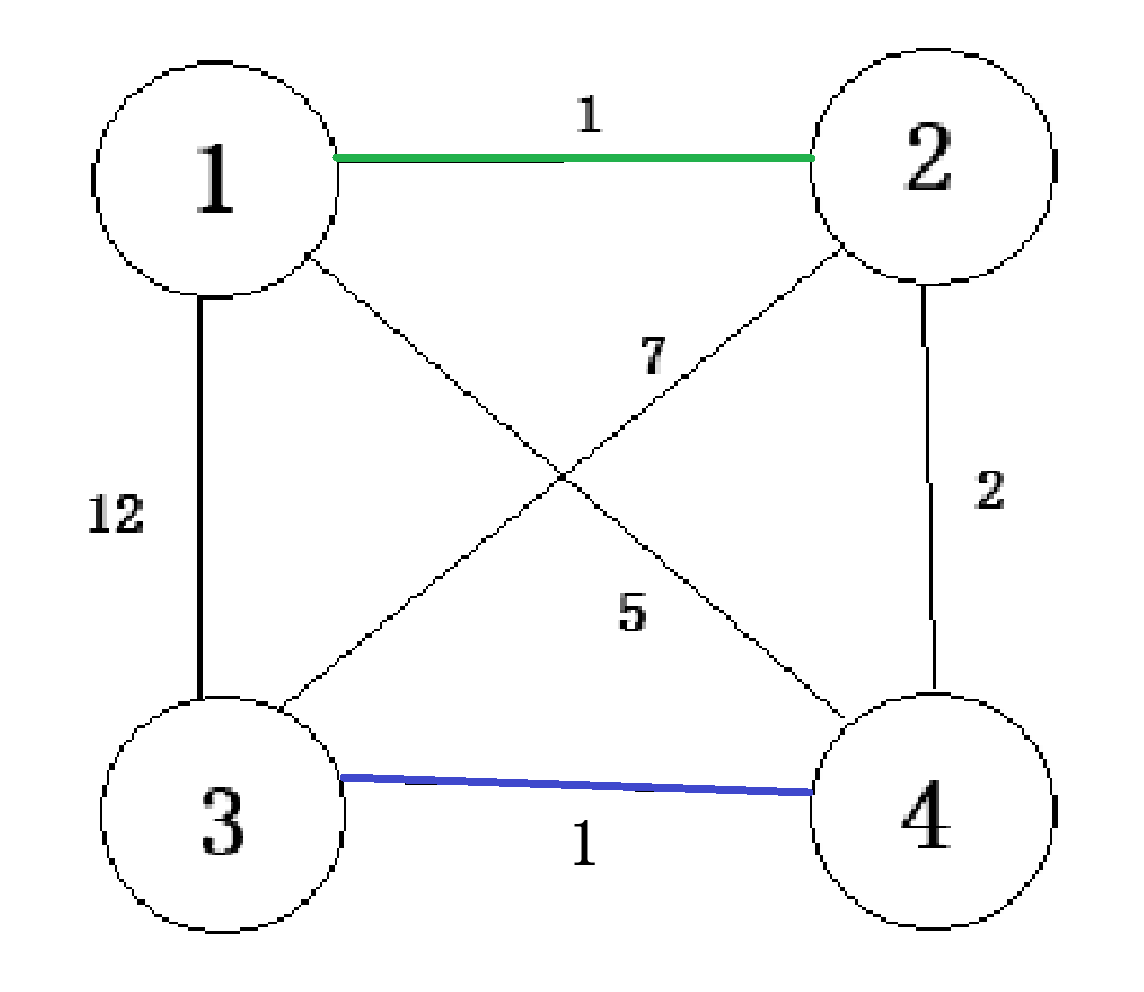
扫描完所有边后，完成。
该算法的时间复杂度为O⁡(mlogm)\operatorname O (m log m)O(mlogm)。

Kruskal⁡\operatorname {Kruskal}Kruskal算法代码

cpp 复制代码

int get(int x)
{
	if(x == fa[x]) return x;
	return fa[x] = get(fa[x]);
}
void Merge()
{
	fa[x] = y;
}
int main()
{
	cin >> n >> m;
	for(int i = 1; i <= m; i++)
		cin >> edge[i].x >> edge[i].y >> edge[i].w;
	sort(edge + 1, edge + 1 + m);
	for(int i = 1; i <= n; i++) fa[i] = i;
	for(int i = 1; i <= m; i++)
	{
		int x = get(edge[i].x);
		int y = get(edge[i].y);
		if (x == y) continue;
		Merge(x, y);
		ans += edge[i].w;
	}
	cout << ans << endl;
	return 0;
}

Prim⁡\operatorname {Prim}Prim算法

原理

该算法的原理仍然是上述定理，但思路是每次维护该最小生成树的一部分。此外，Prim⁡\operatorname {Prim}Prim算法维护的是点集合，而Kruskal⁡\operatorname {Kruskal}Kruskal算法维护的是边集合。

基本实现

一开始，确定节点111属于最小生成树。

随后，我们用集合TTT表示属于最小生成树的节点，用SSS表示不属于的。

然后，在SSS集合中找到距离TTT集合最近的点（距离TTT集合的距离即到任意一个属于TTT集合点的距离的最小值），将其加入集合TTT，累加答案。

循环直到结束。

例如下图：

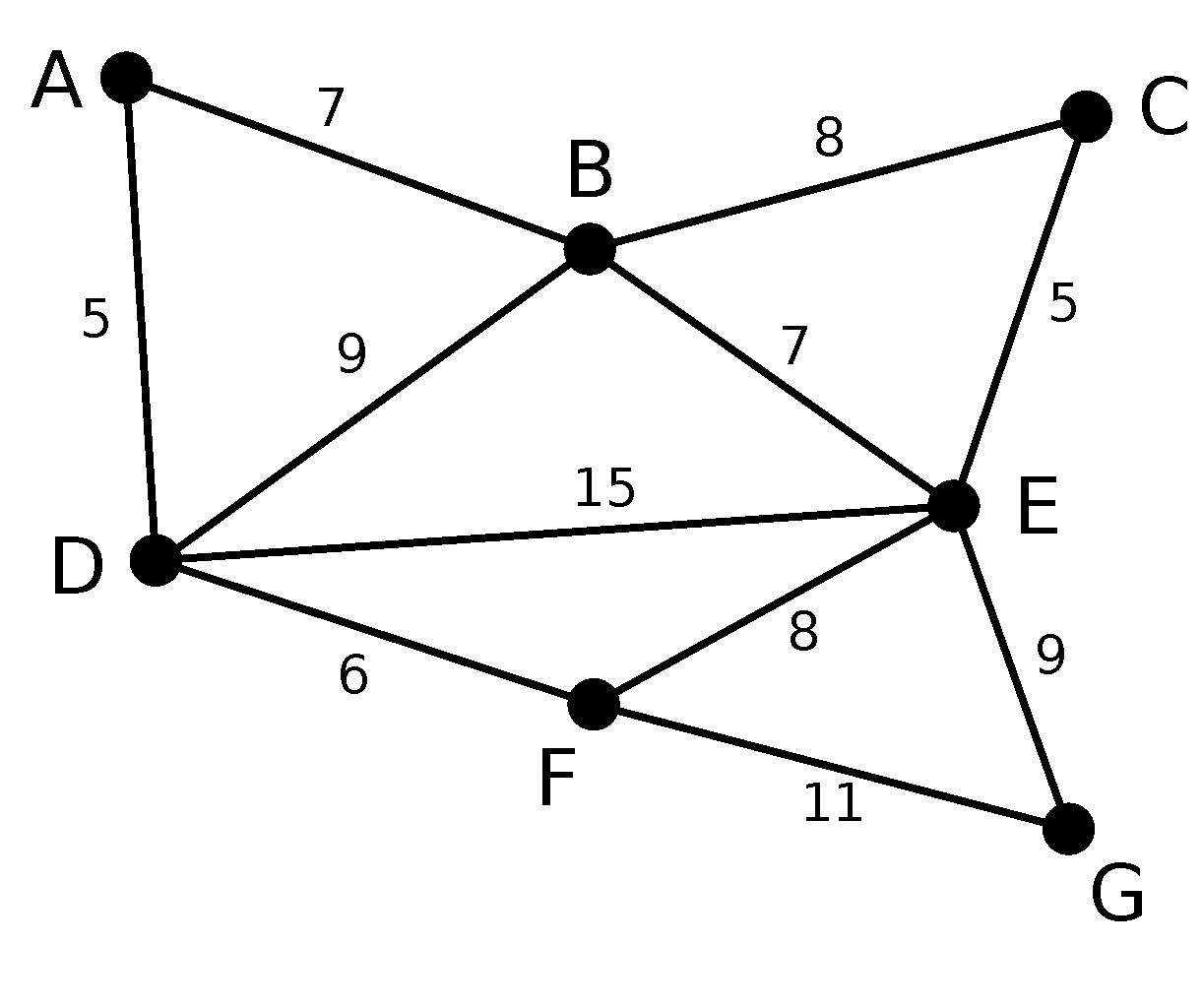
假如从DDD点开始，当前无法到达的位置表示为iii，访问顺序为：

SSS集合	TTT集合	元素距离（顺序A-G）
{D}\{D\}{D}	{A,B,E,F,G,C}\{A,B,E,F,G,C\}{A,B,E,F,G,C}	{5,9,i,0,15,i,i}\{5,9,i,0,15,i,i\}{5,9,i,0,15,i,i}
{D,A}\{D,A\}{D,A}	{B,E,F,G,C}\{B,E,F,G,C\}{B,E,F,G,C}	{5,7,i,0,15,6,i}\{5,7,i,0,15,6,i\}{5,7,i,0,15,6,i}
{D,A,F}\{D,A,F\}{D,A,F}	{B,E,G,C}\{B,E,G,C\}{B,E,G,C}	{5,7,i,0,8,6,11}\{5,7,i,0,8,6,11\}{5,7,i,0,8,6,11}
{D,A,F,B}\{D,A,F,B\}{D,A,F,B}	{E,G,C}\{E,G,C\}{E,G,C}	{5,7,8,0,7,6,i}\{5,7,8,0,7,6,i\}{5,7,8,0,7,6,i}
{D,A,F,B,E}\{D,A,F,B,E\}{D,A,F,B,E}	{G,C}\{G,C\}{G,C}	{5,7,5,0,7,6,9}\{5,7,5,0,7,6,9\}{5,7,5,0,7,6,9}
{D,A,F,B,E,C}\{D,A,F,B,E,C\}{D,A,F,B,E,C}	{G}\{G\}{G}	{5,7,5,0,7,6,9}\{5,7,5,0,7,6,9\}{5,7,5,0,7,6,9}
{D,A,F,B,E,C,G}\{D,A,F,B,E,C,G\}{D,A,F,B,E,C,G}	{}\{\}{}	{5,7,5,0,7,6,9}\{5,7,5,0,7,6,9\}{5,7,5,0,7,6,9}

因此我们可以用一个数组d[x]d[x]d[x]。若xxx属于集合SSS，xxx表示与集合TTT中元素之间权值最小的边的权值。若xxx属于集合TTT,则表示xxx加入集合TTT时所选边的权值。最后，最小生成树权值总和为所有的d[x]d[x]d[x]之和。

代码实现：

cpp 复制代码

int main()
{
	int n;
	cin >> n;
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= n; j++)
			cin >> g[i][j], g[j][i] = g[i][j];
	memset(d, 0x3f, sizeof d);
	d[1] = 0;
	for(int i = 1; i <= n; i++)
	{
		int x = 0;
		for(int j = 1; j <= n; j++) if(!vis[j] && (x == 0 || d[j] < d[x])) x = j;
		vis[x] = true;
		ans += d[x];
		for(int y = 1; y <= n; y++) if(!vis[y]) d[y] = min(d[y], g[x][y]);
	}
	cout << ans << endl;
	return 0;
}

二叉堆优化

在上面的代码实现过程中，我们不难发现，每次对所有点进行遍历找最大值的方法太浪费时间，时间复杂度为O⁡(n2)\operatorname O(n^2)O(n2)。我们可以对其使用二叉堆优化。

代码：

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
const int N = 105;
int g[N][N], dis[N], ans, n;
bool vis[N];
priority_queue < pair < int , int > , vector < pair < int , int > >, greater < pair < int , int > > > q;
int main()
{
	cin >> n;
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= n; j++)
			cin >> g[i][j], g[j][i] = g[i][j];
	memset(dis, 0x3f, sizeof dis);
	q.push({0, 1});
	while(!q.empty())
	{
		int w = q.top().first, x = q.top().second;
		q.pop();
		if(vis[x]) continue;
		vis[x] = true;
		dis[x] = w;
		ans += dis[x];
		for(int y = 1; y <= n; y++)
			if(!vis[y])
			{
				dis[y] = min(dis[y], g[x][y]);
				q.push({g[x][y], y});
			}
	}
	cout << ans << endl;
	return 0;
}

用途总结

尽管使用二叉堆后的Prim⁡\operatorname {Prim}Prim算法时间复杂度为O⁡(mlogn)\operatorname O(m log n)O(mlogn)，但是，Prim⁡\operatorname {Prim}Prim算法远不如Kruskal⁡\operatorname {Kruskal}Kruskal算法方便。因此，Prim⁡\operatorname {Prim}Prim算法主要用于稠密图的最小生成树。在大部分情况下，我们更多的使用Kruskal⁡\operatorname {Kruskal}Kruskal算法。

选择使用哪种方式？

其实很简单。我们只需要比较mmm（边数）和nnn（节点数）的大小。
Kruskal⁡\operatorname {Kruskal}Kruskal算法时间复杂度O⁡(mlogm)\operatorname O(mlogm)O(mlogm)，当mmm大小可以接受，为稀疏图时，首选Kruskal⁡\operatorname {Kruskal}Kruskal。
Prim⁡\operatorname {Prim}Prim算法时间复杂度O⁡(mlogn)\operatorname O(mlogn)O(mlogn)，当mmm加大，为稠密图时，选择Prim⁡\operatorname {Prim}Prim。

图论 最小生成树 MST问题

最小生成树

性质定理

Kruskal⁡\operatorname {Kruskal}Kruskal算法

原理

实现

Prim⁡\operatorname {Prim}Prim算法

原理

基本实现

二叉堆优化

用途总结

图论最小生成树 MST问题