《数字图像处理》第 12 章 - 图像模式分类

大家好！今天给大家带来《数字图像处理》第 12 章 ------ 图像模式分类的完整解析，这一章是数字图像处理从 "分析" 到 "决策" 的关键环节，不管是传统的图像识别还是当下火热的深度学习图像分类，都离不开这一章的理论基础。

引言

在数字图像处理的应用场景中，我们常常需要对图像中的目标进行 "归类"------ 比如区分照片中的猫和狗、识别手写数字、检测医学影像中的病变区域，这些任务的本质都是图像模式分类：通过提取图像的特征信息，结合一定的分类规则，将未知类别的图像（或图像区域）分配到预先定义好的模式类中。

从传统的最小距离分类器、贝叶斯分类器，到现代的神经网络、深度卷积神经网络（CNN），图像模式分类技术经历了从简单到复杂、从浅层特征到深层特征的发展历程。本章将系统梳理这些技术的原理与实现，帮助大家搭建起完整的图像模式分类知识体系。

学习目标

1. 理解模式、模式类、模式向量的核心概念，掌握结构模式与统计模式的区别；
2. 掌握原型匹配模式分类的各类方法（最小距离、相关匹配、SIFT 特征匹配等），并能编程实现；
3. 推导贝叶斯分类器的核心公式，掌握高斯模式类下贝叶斯分类器的应用；
4. 理解神经网络的基础原理，掌握感知机、多层前馈神经网络的工作机制及反向传播算法；
5. 掌握深度卷积神经网络的结构与原理，能实现简单 CNN 的训练与图像分类；
6. 了解图像模式分类实现中的关键细节，具备解决实际图像分类问题的能力。

12.1 背景

图像模式分类的本质是从图像数据中学习分类规则，并利用该规则对未知图像进行类别判断。其发展大致可分为三个阶段：

1. 传统手工特征分类阶段 ：该阶段依赖人工设计特征（如纹理、形状、颜色特征），结合传统机器学习算法（如 K 近邻、SVM、贝叶斯分类器）实现分类，优点是原理清晰、计算量小，缺点是特征设计依赖经验，泛化能力弱，难以应对复杂图像场景；
2. 浅层神经网络阶段 ：以感知机、多层前馈神经网络为代表，通过简单的网络结构自动学习特征，一定程度上摆脱了手工特征的限制，但由于网络深度不足，难以提取图像的深层语义特征；
3. 深度学习阶段 ：以深度卷积神经网络为核心，利用多层卷积、池化结构自动提取图像的底层（如边缘、纹理）、中层（如部件、形状）和高层（如类别、语义）特征，泛化能力强，在图像分类、目标检测等任务中取得了突破性进展，成为当前图像模式分类的主流技术。

12.2 模式与模式类

12.2.1 模式向量

模式 （Pattern）是指具有某种共性的事物的集合表现，在图像领域，模式可以是一幅图像、一个图像区域、一个像素点（及其邻域）。

为了便于计算机处理，我们通常将模式转换为模式向量（Pattern Vector）------ 将模式的特征信息进行量化，组织成一维向量的形式。对于图像而言，模式向量的构建有两种常见方式：

模式向量的数学表示：

12.2.2 结构模式

模式类 （Pattern Class）是指具有相同属性的模式的集合，通常用ω1​,ω2​,...,ωc​表示，其中c为类别数量（如猫、狗两类分类任务中，c=2）。

根据模式的表示形式，模式类可分为统计模式 和结构模式：

统计模式：以模式向量为基础，通过统计特征（如均值、方差、概率密度）描述模式类的特性，适用于特征可量化、无明显结构关系的场景（如灰度图像分类、颜色分类）；

结构模式：关注模式的内部结构关系（如形状的轮廓、纹理的排列、目标的部件组合），通过语法规则、图结构等形式描述模式类，适用于具有明显结构特征的场景（如字符识别、形状识别）。

例如，手写数字 "8" 的结构模式可描述为 "两个闭合圆上下堆叠，中间有连接"，而其统计模式可表示为像素灰度值组成的模式向量及对应的统计特征。

12.3 原型匹配模式分类

原型匹配模式分类的核心思想是：为每个模式类预先定义一个或多个原型（代表该类的典型模式），通过计算未知模式与各类原型的相似度，将未知模式分配给相似度最高的原型所属类别。

12.3.1 最小距离分类器

原理

可运行代码与效果对比

下面以手写数字（0-9）分类为例，实现最小距离分类器，并展示效果对比：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 解决matplotlib中文显示问题
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False  # 解决负号显示问题

# 1. 加载数据并预处理
digits = load_digits()
X = digits.data  # 模式向量（像素级，8x8图像展开为64维向量）
y = digits.target  # 标签（0-9）

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 2. 计算每个类别的均值向量（原型）
classes = np.unique(y_train)
class_means = {}  # 存储每个类别的均值向量
for cls in classes:
    # 提取该类别的所有样本
    cls_samples = X_train[y_train == cls]
    # 计算均值向量
    cls_mean = np.mean(cls_samples, axis=0)
    class_means[cls] = cls_mean

# 3. 实现最小距离分类器
def min_distance_classifier(x, class_means):
    """
    最小距离分类器预测单个样本
    :param x: 未知样本的模式向量
    :param class_means: 各类别均值向量字典
    :return: 预测类别
    """
    min_dist = float('inf')
    pred_cls = -1
    for cls, mean_vec in class_means.items():
        # 计算欧式距离
        dist = np.linalg.norm(x - mean_vec)
        if dist < min_dist:
            min_dist = dist
            pred_cls = cls
    return pred_cls

# 4. 对测试集进行预测
y_pred = [min_distance_classifier(x, class_means) for x in X_test]

# 5. 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"最小距离分类器测试集准确率：{accuracy:.4f}")

# 6. 效果可视化：展示部分测试样本的真实标签与预测标签
fig, axes = plt.subplots(2, 5, figsize=(12, 6))
axes = axes.flatten()
for i in range(10):
    # 还原图像（64维向量转为8x8）
    img = X_test[i].reshape(8, 8)
    axes[i].imshow(img, cmap='gray')
    axes[i].set_title(f"真实：{y_test[i]}\n预测：{y_pred[i]}")
    axes[i].axis('off')
plt.suptitle("最小距离分类器效果对比（部分样本）", fontsize=14)
plt.tight_layout()
plt.show()

# 7. 可视化各类别均值原型（每个类别的典型图像）
fig, axes = plt.subplots(2, 5, figsize=(12, 6))
axes = axes.flatten()
for cls in classes:
    mean_img = class_means[cls].reshape(8, 8)
    axes[cls].imshow(mean_img, cmap='gray')
    axes[cls].set_title(f"类别{cls}均值原型")
    axes[cls].axis('off')
plt.suptitle("各类别均值原型图像", fontsize=14)
plt.tight_layout()
plt.show()

效果说明

运行代码后，会输出最小距离分类器的测试集准确率（约 90% 左右），并展示两张对比图：

1. 部分测试样本的真实标签与预测标签对比图：直观展示分类的正确与错误情况；
2. 各类别均值原型图像：展示每个数字类别的典型特征，这是最小距离分类的匹配依据。

12.3.2 对二维原型匹配使用相关

原理

可运行代码与效果对比

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 解决matplotlib中文显示问题
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 加载数据并预处理（保留二维图像格式，不展开为一维向量）
digits = load_digits()
X = digits.images  # 二维图像格式，(1797, 8, 8)
y = digits.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 2. 计算每个类别的均值原型（二维图像）
classes = np.unique(y_train)
class_2d_means = {}
for cls in classes:
    cls_samples = X_train[y_train == cls]
    cls_2d_mean = np.mean(cls_samples, axis=0)
    class_2d_means[cls] = cls_2d_mean

# 3. 基于互相关的匹配分类器
def cross_correlation_classifier(img, class_2d_means):
    """
    互相关匹配分类器
    :param img: 未知二维图像
    :param class_2d_means: 各类别二维均值原型字典
    :return: 预测类别
    """
    max_corr = -float('inf')
    pred_cls = -1
    for cls, proto_img in class_2d_means.items():
        # 计算互相关值（对齐情况下）
        corr = np.sum(proto_img * img)
        if corr > max_corr:
            max_corr = corr
            pred_cls = cls
    return pred_cls

# 4. 对测试集进行预测
y_corr_pred = [cross_correlation_classifier(img, class_2d_means) for img in X_test]

# 5. 计算准确率
corr_accuracy = accuracy_score(y_test, y_corr_pred)
print(f"互相关匹配分类器测试集准确率：{corr_accuracy:.4f}")

# 6. 效果可视化：对比真实标签与预测标签
fig, axes = plt.subplots(2, 5, figsize=(12, 6))
axes = axes.flatten()
for i in range(10):
    axes[i].imshow(X_test[i], cmap='gray')
    axes[i].set_title(f"真实：{y_test[i]}\n预测：{y_corr_pred[i]}")
    axes[i].axis('off')
plt.suptitle("互相关匹配分类器效果对比（部分样本）", fontsize=14)
plt.tight_layout()
plt.show()

# 7. 可视化互相关值分布（以类别0和类别1为例）
cls0_proto = class_2d_means[0]
cls1_proto = class_2d_means[1]
# 提取测试集中类别0和类别1的样本
cls0_test_samples = X_test[y_test == 0]
cls1_test_samples = X_test[y_test == 1]

# 计算类别0样本与两个原型的互相关值
cls0_corr0 = [np.sum(sample * cls0_proto) for sample in cls0_test_samples]
cls0_corr1 = [np.sum(sample * cls1_proto) for sample in cls0_test_samples]

# 计算类别1样本与两个原型的互相关值
cls1_corr0 = [np.sum(sample * cls0_proto) for sample in cls1_test_samples]
cls1_corr1 = [np.sum(sample * cls1_proto) for sample in cls1_test_samples]

# 绘制箱线图对比
fig, ax = plt.subplots(1, 1, figsize=(10, 6))
box_data = [cls0_corr0, cls0_corr1, cls1_corr0, cls1_corr1]
labels = ["类别0样本与0原型", "类别0样本与1原型", "类别1样本与0原型", "类别1样本与1原型"]
ax.boxplot(box_data, labels=labels)
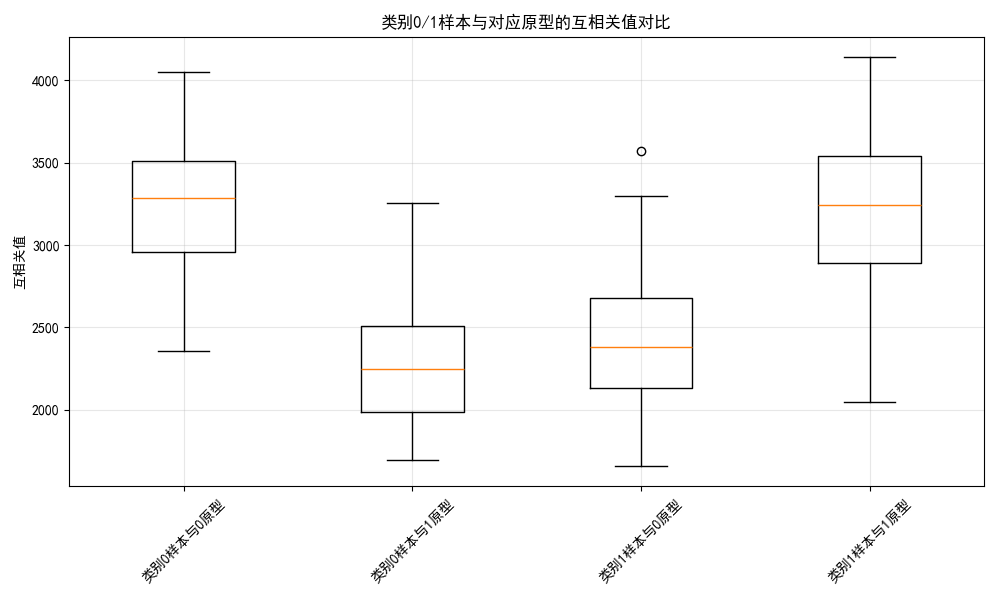
ax.set_title("类别0/1样本与对应原型的互相关值对比")
ax.set_ylabel("互相关值")
ax.grid(alpha=0.3)
plt.xticks(rotation=45)
plt.tight_layout()
plt.show()

效果说明

代码运行后，输出互相关匹配分类器的准确率（与最小距离分类器接近），并展示两张对比图：

1. 部分测试样本的分类效果对比：直观查看分类结果；
2. 类别 0/1 样本与原型的互相关值箱线图：可以看到，同类样本与原型的互相关值明显高于异类样本，验证了互相关匹配的有效性。

12.3.3 匹配 SIFT 特征

原理

SIFT（Scale-Invariant Feature Transform，尺度不变特征变换）是一种具有尺度不变性、旋转不变性的局部特征描述子，能够在不同尺度、旋转、光照条件下提取图像的稳定特征。

SIFT 特征匹配分类的流程为：

1. 为每个模式类的原型图像提取 SIFT 特征点及描述子；
2. 为未知图像提取 SIFT 特征点及描述子；
3. 使用特征匹配算法（如 K 近邻匹配、FLANN 匹配）计算未知图像与原型图像的特征匹配对数量；
4. 匹配对数量最多的原型所属类别即为未知图像的类别。

可运行代码与效果对比

import cv2
import numpy as np
import matplotlib.pyplot as plt
import os

# 解决matplotlib中文显示问题
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False

# 注意：需要确保安装了opencv-contrib-python（包含SIFT算法）
# 安装命令：pip install opencv-contrib-python==4.5.5.62

# 1. 准备原型图像（手动创建或下载简单图像，这里以自制简单形状为例）
# 先创建保存原型图像的临时目录
if not os.path.exists("sift_prototypes"):
    os.makedirs("sift_prototypes")

# 创建3类原型图像：圆形、正方形、三角形
def create_prototype_images():
    # 圆形原型
    circle_img = np.zeros((200, 200), dtype=np.uint8)
    cv2.circle(circle_img, (100, 100), 80, 255, -1)
    cv2.imwrite("sift_prototypes/circle.jpg", circle_img)
    
    # 正方形原型
    square_img = np.zeros((200, 200), dtype=np.uint8)
    cv2.rectangle(square_img, (40, 40), (160, 160), 255, -1)
    cv2.imwrite("sift_prototypes/square.jpg", square_img)
    
    # 三角形原型
    triangle_img = np.zeros((200, 200), dtype=np.uint8)
    pts = np.array([[100, 40], [40, 160], [160, 160]], np.int32)
    cv2.fillPoly(triangle_img, [pts], 255)
    cv2.imwrite("sift_prototypes/triangle.jpg", triangle_img)

# 创建原型图像
create_prototype_images()

# 2. 加载原型图像并提取SIFT特征
proto_classes = ["circle", "square", "triangle"]
proto_sift = {}  # 存储每个类别的SIFT描述子
sift = cv2.SIFT_create()

for cls in proto_classes:
    img_path = f"sift_prototypes/{cls}.jpg"
    img = cv2.imread(img_path, 0)
    # 提取SIFT特征点和描述子
    kp, des = sift.detectAndCompute(img, None)
    proto_sift[cls] = (img, kp, des)
    # 绘制特征点
    img_with_kp = cv2.drawKeypoints(img, kp, None, flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
    plt.imshow(img_with_kp, cmap='gray')
    plt.title(f"{cls}原型图像及SIFT特征点")
    plt.axis('off')
    plt.show()

# 3. 创建测试图像（带旋转、缩放的形状）
def create_test_images():
    if not os.path.exists("sift_test"):
        os.makedirs("sift_test")
    
    # 旋转缩放后的圆形
    circle_test = np.zeros((200, 200), dtype=np.uint8)
    cv2.circle(circle_test, (100, 100), 60, 255, -1)
    # 旋转45度
    M = cv2.getRotationMatrix2D((100, 100), 45, 1)
    circle_test_rot = cv2.warpAffine(circle_test, M, (200, 200))
    cv2.imwrite("sift_test/circle_test.jpg", circle_test_rot)
    
    # 旋转缩放后的正方形
    square_test = np.zeros((200, 200), dtype=np.uint8)
    cv2.rectangle(square_test, (50, 50), (150, 150), 255, -1)
    M = cv2.getRotationMatrix2D((100, 100), 30, 0.8)
    square_test_rot = cv2.warpAffine(square_test, M, (200, 200))
    cv2.imwrite("sift_test/square_test.jpg", square_test_rot)
    
    # 旋转缩放后的三角形
    triangle_test = np.zeros((200, 200), dtype=np.uint8)
    pts = np.array([[100, 50], [50, 150], [150, 150]], np.int32)
    cv2.fillPoly(triangle_test, [pts], 255)
    M = cv2.getRotationMatrix2D((100, 100), 60, 1.2)
    triangle_test_rot = cv2.warpAffine(triangle_test, M, (200, 200))
    cv2.imwrite("sift_test/triangle_test.jpg", triangle_test_rot)

# 创建测试图像
create_test_images()

# 4. SIFT特征匹配分类
def sift_classify(test_img_path, proto_sift, flann_index=0):
    """
    SIFT特征匹配分类
    :param test_img_path: 测试图像路径
    :param proto_sift: 原型图像SIFT特征字典
    :param flann_index: FLANN匹配器索引类型
    :return: 预测类别、匹配可视化图像
    """
    # 加载测试图像并提取SIFT特征
    test_img = cv2.imread(test_img_path, 0)
    test_kp, test_des = sift.detectAndCompute(test_img, None)
    if test_des is None:
        return "未知类别", None
    
    # 初始化FLANN匹配器
    FLANN_INDEX_KDTREE = flann_index
    index_params = dict(algorithm=FLANN_INDEX_KDTREE, trees=5)
    search_params = dict(checks=50)
    flann = cv2.FlannBasedMatcher(index_params, search_params)
    
    max_matches = 0
    pred_cls = "未知类别"
    best_match_img = None
    
    for cls, (proto_img, proto_kp, proto_des) in proto_sift.items():
        if proto_des is None:
            continue
        # K近邻匹配
        matches = flann.knnMatch(proto_des, test_des, k=2)
        # 应用Lowe's比率测试筛选优质匹配
        good_matches = []
        for m, n in matches:
            if m.distance < 0.7 * n.distance:
                good_matches.append(m)
        
        # 记录匹配数最多的类别
        if len(good_matches) > max_matches:
            max_matches = len(good_matches)
            pred_cls = cls
            # 绘制匹配图像
            best_match_img = cv2.drawMatches(proto_img, proto_kp, test_img, test_kp, good_matches, None,
                                             flags=cv2.DrawMatchesFlags_NOT_DRAW_SINGLE_POINTS)
    
    return pred_cls, best_match_img

# 5. 对每个测试图像进行分类并可视化
test_images = ["circle_test.jpg", "square_test.jpg", "triangle_test.jpg"]
for test_img_name in test_images:
    test_img_path = f"sift_test/{test_img_name}"
    pred_cls, match_img = sift_classify(test_img_path, proto_sift)
    print(f"测试图像{test_img_name}的预测类别：{pred_cls}")
    
    if match_img is not None:
        # 转换为RGB格式（opencv默认BGR）
        match_img_rgb = cv2.cvtColor(match_img, cv2.COLOR_BGR2RGB)
        plt.imshow(match_img_rgb)
        plt.title(f"{test_img_name}与{pred_cls}原型的SIFT匹配效果")
        plt.axis('off')
        plt.show()

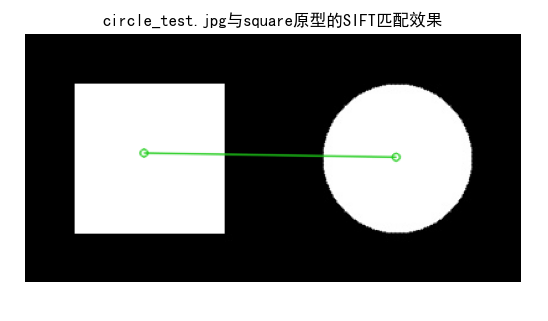
效果说明

代码运行后，会先创建圆形、正方形、三角形的原型图像和带旋转 / 缩放的测试图像，然后提取 SIFT 特征并展示，最后通过 FLANN 匹配实现分类，输出预测结果并展示特征匹配对比图，可直观看到同类图像的 SIFT 特征匹配对更多，验证了 SIFT 特征的稳定性和匹配有效性。

12.3.4 匹配结构原型

原理

结构原型匹配适用于具有明显结构特征的模式（如字符、形状），其核心是：用结构描述符（如图、语法、字符串）表示原型和未知模式，通过结构匹配算法（如图匹配、语法分析）判断二者的结构相似度，进而实现分类。

以简单的形状结构匹配为例，我们可以用形状的轮廓点序列、顶点数量、边数等结构特征作为匹配依据，例如：

• 圆形：轮廓无明显顶点，边数为 1（闭合曲线）；
• 正方形：4 个顶点，4 条等长直边，邻边垂直；
• 三角形：3 个顶点，3 条直边。

通过提取未知形状的结构特征，与各类别结构原型的特征进行匹配，即可完成分类。

可运行代码与效果对比

import cv2
import numpy as np
import matplotlib.pyplot as plt
import os

# 解决matplotlib中文显示问题
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 定义结构原型（形状的结构特征：顶点数、边数、轮廓面积比）
structure_prototypes = {
    "circle": {"vertex_num": 0, "edge_num": 1, "area_ratio": 0.785},  # 圆面积/外接正方形面积≈π/4≈0.785
    "square": {"vertex_num": 4, "edge_num": 4, "area_ratio": 1.0},  # 正方形面积/外接正方形面积=1.0
    "triangle": {"vertex_num": 3, "edge_num": 3, "area_ratio": 0.433}  # 正三角形面积/外接正方形面积≈√3/4≈0.433
}


# 2. 提取形状的结构特征
def extract_structure_features(img_path):
    """
    提取形状的结构特征
    :param img_path: 图像路径
    :return: 顶点数、边数、面积比
    """
    # 检查文件是否存在
    if not os.path.exists(img_path):
        print(f"错误：图像文件 {img_path} 不存在！")
        return 0, 0, 0

    # 加载图像
    img = cv2.imread(img_path, 0)
    if img is None:
        print(f"错误：无法加载图像 {img_path}！")
        return 0, 0, 0

    # 二值化（阈值分割）
    _, binary_img = cv2.threshold(img, 127, 255, cv2.THRESH_BINARY)
    # 提取轮廓
    contours, _ = cv2.findContours(binary_img, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
    if len(contours) == 0:
        print("警告：未提取到图像轮廓！")
        return 0, 0, 0

    main_contour = max(contours, key=cv2.contourArea)
    # 计算轮廓面积
    contour_area = cv2.contourArea(main_contour)
    # 计算外接正方形
    x, y, w, h = cv2.boundingRect(main_contour)
    square_area = w * h
    area_ratio = contour_area / square_area if square_area != 0 else 0

    # 多边形逼近（提取顶点）
    epsilon = 0.02 * cv2.arcLength(main_contour, True)
    approx = cv2.approxPolyDP(main_contour, epsilon, True)
    vertex_num = len(approx)
    edge_num = vertex_num  # 闭合多边形边数=顶点数

    # 特殊处理圆形（顶点数≥8时判定为圆）
    if vertex_num >= 8:
        vertex_num_cal = 0
        edge_num_cal = 1
    else:
        vertex_num_cal = vertex_num
        edge_num_cal = edge_num

    return vertex_num_cal, edge_num_cal, area_ratio


# 3. 结构原型匹配分类
def structure_match_classify(img_path, structure_prototypes):
    """
    结构原型匹配分类
    :param img_path: 测试图像路径
    :param structure_prototypes: 结构原型字典
    :return: 预测类别、结构特征
    """
    vertex_num, edge_num, area_ratio = extract_structure_features(img_path)
    min_feature_dist = float('inf')
    pred_cls = "未知类别"

    for cls, proto_feat in structure_prototypes.items():
        # 计算特征距离（加权和）
        v_dist = abs(vertex_num - proto_feat["vertex_num"])
        e_dist = abs(edge_num - proto_feat["edge_num"])
        a_dist = abs(area_ratio - proto_feat["area_ratio"])
        total_dist = v_dist * 0.4 + e_dist * 0.4 + a_dist * 0.2  # 加权分配
        if total_dist < min_feature_dist:
            min_feature_dist = total_dist
            pred_cls = cls

    return pred_cls, (vertex_num, edge_num, area_ratio)


# 4. 初始化画布（创建单个窗口，包含3个子图）
fig, axes = plt.subplots(1, 3, figsize=(15, 5))  # 1行3列的子图布局，设置画布大小
fig.suptitle("形状结构原型匹配分类结果", fontsize=16, fontweight='bold')  # 总标题

# 5. 遍历测试图像进行分类和可视化
test_images = ["circle_test.jpg", "square_test.jpg", "triangle_test.jpg"]
for idx, test_img_name in enumerate(test_images):
    test_img_path = f"sift_test/{test_img_name}"
    # 调用分类函数获取结果
    pred_cls, features = structure_match_classify(test_img_path, structure_prototypes)
    vertex_num, edge_num, area_ratio = features

    print(f"\n测试图像：{test_img_name}")
    print(f"提取的结构特征：顶点数={vertex_num}, 边数={edge_num}, 面积比={area_ratio:.3f}")
    print(f"预测类别：{pred_cls}")

    # 绘制当前图像到对应子图
    ax = axes[idx]  # 获取当前子图对象
    if os.path.exists(test_img_path) and cv2.imread(test_img_path) is not None:
        img = cv2.imread(test_img_path)
        img_rgb = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
        # 提取轮廓用于绘制
        gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
        _, binary = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
        contours, _ = cv2.findContours(binary, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
        if len(contours) > 0:
            cv2.drawContours(img_rgb, contours, -1, (255, 0, 0), 2)
            # 绘制多边形逼近
            main_contour = max(contours, key=cv2.contourArea)
            epsilon = 0.02 * cv2.arcLength(main_contour, True)
            approx = cv2.approxPolyDP(main_contour, epsilon, True)
            cv2.drawContours(img_rgb, [approx], -1, (0, 255, 0), 2)

        ax.imshow(img_rgb)
        ax.set_title(f"{test_img_name}\n预测：{pred_cls}（顶点数：{vertex_num}）", fontsize=12)
    else:
        ax.text(0.5, 0.5, "图像加载失败", ha='center', va='center', fontsize=12)
        ax.set_title(test_img_name, fontsize=12)

    ax.axis('off')  # 关闭子图坐标轴

# 调整子图间距，避免标题重叠
plt.tight_layout(rect=[0, 0, 1, 0.95])  # rect参数预留总标题空间
# 显示单个窗口（包含所有子图）
plt.show()

效果说明

代码运行后，会提取测试形状的结构特征（顶点数、边数、面积比），与结构原型进行匹配，输出预测结果，并展示图像的轮廓（蓝色）和多边形逼近（绿色），直观呈现结构特征的提取过程，验证结构原型匹配的有效性。

12.4 最优（贝叶斯）统计分类器

贝叶斯分类器是基于贝叶斯定理的统计分类器，其核心思想是：通过计算未知模式属于各类别的后验概率，将未知模式分配给后验概率最大的类别。由于贝叶斯分类器在理论上能达到最小的分类错误率（称为贝叶斯错误率），因此被称为最优统计分类器。

12.4.1 贝叶斯分类器的推导

核心定理

分类规则

12.4.2 高斯模式类的贝叶斯分类器

类条件概率密度假设

可运行代码与效果对比

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from scipy.stats import multivariate_normal

# 解决matplotlib中文显示问题
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 加载数据并预处理
digits = load_digits()
X = digits.data
y = digits.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 2. 估计贝叶斯分类器的参数（先验概率、均值向量、协方差矩阵）
classes = np.unique(y_train)
n_classes = len(classes)
d = X_train.shape[1]  # 特征维度

# 先验概率 P(ω_i)
prior_probs = {}
for cls in classes:
    prior_probs[cls] = np.sum(y_train == cls) / len(y_train)

# 均值向量 m_i
class_means = {}
for cls in classes:
    class_means[cls] = np.mean(X_train[y_train == cls], axis=0)

# 协方差矩阵 Σ_i（添加微小扰动避免奇异）
class_covs = {}
epsilon = 1e-6  # 防止协方差矩阵奇异
for cls in classes:
    cls_samples = X_train[y_train == cls]
    cov = np.cov(cls_samples, rowvar=False)
    class_covs[cls] = cov + epsilon * np.eye(d)

# 3. 高斯贝叶斯分类器
def gaussian_bayes_classifier(x, classes, prior_probs, class_means, class_covs):
    """
    高斯模式类贝叶斯分类器
    :param x: 未知模式向量
    :param classes: 类别列表
    :param prior_probs: 先验概率字典
    :param class_means: 均值向量字典
    :param class_covs: 协方差矩阵字典
    :return: 预测类别
    """
    max_g = -float('inf')
    pred_cls = -1
    for cls in classes:
        m_i = class_means[cls]
        cov_i = class_covs[cls]
        prior_i = prior_probs[cls]
        
        # 计算类条件概率密度 P(x|ω_i)
        try:
            p_x_wi = multivariate_normal.pdf(x, mean=m_i, cov=cov_i)
        except:
            p_x_wi = 1e-20  # 异常情况赋值极小值
        
        # 计算判别函数 g_i(x) = ln(P(x|ω_i)) + ln(P(ω_i))
        if p_x_wi == 0:
            g_i = -float('inf')
        else:
            g_i = np.log(p_x_wi) + np.log(prior_i)
        
        if g_i > max_g:
            max_g = g_i
            pred_cls = cls
    return pred_cls

# 4. 对测试集进行预测
y_bayes_pred = [gaussian_bayes_classifier(x, classes, prior_probs, class_means, class_covs) for x in X_test]

# 5. 计算准确率并对比最小距离分类器
bayes_accuracy = accuracy_score(y_test, y_bayes_pred)
print(f"高斯贝叶斯分类器测试集准确率：{bayes_accuracy:.4f}")

# 加载之前最小距离分类器的结果（重新运行最小距离分类器）
def min_distance_classifier(x, class_means):
    min_dist = float('inf')
    pred_cls = -1
    for cls, mean_vec in class_means.items():
        dist = np.linalg.norm(x - mean_vec)
        if dist < min_dist:
            min_dist = dist
            pred_cls = cls
    return pred_cls

y_min_dist_pred = [min_distance_classifier(x, class_means) for x in X_test]
min_dist_accuracy = accuracy_score(y_test, y_min_dist_pred)
print(f"最小距离分类器测试集准确率：{min_dist_accuracy:.4f}")

# 6. 效果可视化：准确率对比
methods = ["高斯贝叶斯分类器", "最小距离分类器"]
accuracies = [bayes_accuracy, min_dist_accuracy]

plt.bar(methods, accuracies, width=0.5, color=['#1f77b4', '#ff7f0e'])
plt.ylim(0, 1)
plt.ylabel("测试集准确率")
plt.title("高斯贝叶斯分类器与最小距离分类器准确率对比")
for i, acc in enumerate(accuracies):
    plt.text(i, acc + 0.02, f"{acc:.4f}", ha='center', fontsize=12)
plt.grid(alpha=0.3, axis='y')
plt.show()

# 7. 可视化部分样本的分类结果
fig, axes = plt.subplots(2, 5, figsize=(12, 6))
axes = axes.flatten()
for i in range(10):
    img = X_test[i].reshape(8, 8)
    axes[i].imshow(img, cmap='gray')
    axes[i].set_title(f"真实：{y_test[i]}\n贝叶斯预测：{y_bayes_pred[i]}\n最小距离预测：{y_min_dist_pred[i]}")
    axes[i].axis('off')
plt.suptitle("两种分类器效果对比（部分样本）", fontsize=14)
plt.tight_layout()
plt.show()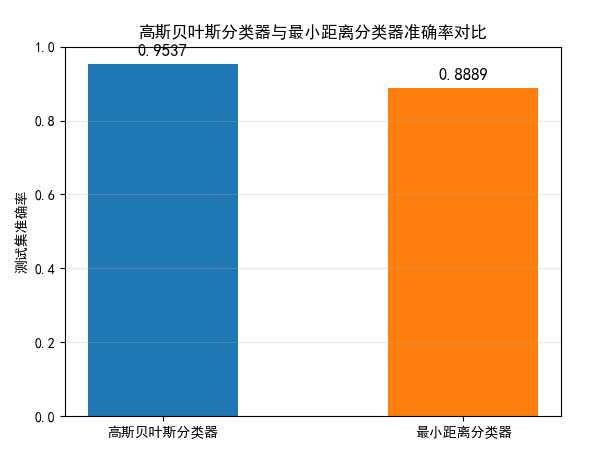

效果说明

代码运行后，会输出高斯贝叶斯分类器和最小距离分类器的准确率，通常高斯贝叶斯分类器的准确率更高（考虑了协方差矩阵的影响，更贴合数据分布），并展示两张对比图：

1. 两种分类器的准确率柱状图：直观对比性能差异；
2. 部分样本的分类结果对比：展示两种分类器的预测情况，验证贝叶斯分类器的优越性。

12.5 神经网络与深度学习

12.5.5 使用反向传播训练深层神经网络

原理补充

反向传播（Backpropagation）是训练深层神经网络的核心算法，其核心思想是：通过计算损失函数对各层权重和偏置的梯度，从输出层向输入层逐层传递梯度，并利用梯度下降算法更新权重和偏置。

其中，各关键梯度的推导基于链式法则：

完整可运行代码与效果对比

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 解决matplotlib中文显示问题
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 生成复杂非线性可分数据（环形数据，比月亮数据更难分类）
X, y = make_circles(n_samples=400, noise=0.1, factor=0.5, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 2. 实现基于反向传播的深层神经网络
class DeepNN:
    def __init__(self, layer_sizes, learning_rate=0.05, max_iter=5000):
        """
        深层神经网络（支持多层隐藏层）
        :param layer_sizes: 层大小列表，如[2, 16, 8, 2]（输入层2→隐藏层16→隐藏层8→输出层2）
        :param learning_rate: 学习率
        :param max_iter: 最大迭代次数
        """
        self.layer_sizes = layer_sizes  # 各层神经元数量
        self.lr = learning_rate          # 学习率
        self.max_iter = max_iter        # 最大迭代次数
        self.weights = []                # 存储各层权重 W^(l)
        self.biases = []                 # 存储各层偏置 b^(l)
        self.num_layers = len(layer_sizes)  # 网络总层数（含输入层、输出层）
        self.loss_history = []           # 记录训练损失变化

    def relu(self, z):
        """ReLU激活函数：引入非线性，缓解梯度消失"""
        return np.maximum(0, z)

    def relu_deriv(self, z):
        """ReLU激活函数的导数"""
        return np.where(z > 0, 1, 0)

    def softmax(self, z):
        """Softmax激活函数：输出层多分类，将结果转为概率分布"""
        # 减去最大值防止指数溢出
        exp_z = np.exp(z - np.max(z, axis=1, keepdims=True))
        return exp_z / np.sum(exp_z, axis=1, keepdims=True)

    def forward(self, X):
        """
        正向传播：计算各层的加权和z和激活输出a
        :param X: 输入数据 (n_samples, input_size)
        :return: zs（各层z值）、activations（各层a值）
        """
        activations = [X]  # 第0层激活输出=输入数据
        zs = []            # 存储第1层到输出层的z值
        a = X              # 当前层激活输出

        # 逐层计算
        for i in range(self.num_layers - 1):
            w = self.weights[i]
            b = self.biases[i]
            z = np.dot(a, w) + b  # 计算当前层加权和 z^(l)
            zs.append(z)

            # 根据层类型选择激活函数
            if i < self.num_layers - 2:  # 隐藏层：使用ReLU
                a = self.relu(z)
            else:  # 输出层：使用Softmax
                a = self.softmax(z)
            activations.append(a)

        return zs, activations

    def backward(self, zs, activations, y_one_hot):
        """
        反向传播：计算各层权重和偏置的梯度
        :param zs: 正向传播的z值列表
        :param activations: 正向传播的a值列表
        :param y_one_hot: 真实标签的one-hot编码 (n_samples, output_size)
        :return: weight_grads（权重梯度）、bias_grads（偏置梯度）
        """
        n_samples = y_one_hot.shape[0]
        # 初始化梯度存储（与权重/偏置形状一致）
        weight_grads = [np.zeros_like(w) for w in self.weights]
        bias_grads = [np.zeros_like(b) for b in self.biases]

        # 1. 计算输出层（第L层）的梯度 δ^L
        delta = activations[-1] - y_one_hot  # Softmax+交叉熵损失的梯度简化结果
        # 输出层权重梯度 ∂L/∂W^L
        weight_grads[-1] = np.dot(activations[-2].T, delta) / n_samples
        # 输出层偏置梯度 ∂L/∂b^L
        bias_grads[-1] = np.mean(delta, axis=0, keepdims=True)

        # 2. 反向计算各隐藏层的梯度
        for l in range(self.num_layers - 3, -1, -1):
            # 当前层的z值
            z = zs[l]
            # 计算当前层梯度 δ^l
            delta = np.dot(delta, self.weights[l+1].T) * self.relu_deriv(z)
            # 当前层权重梯度 ∂L/∂W^l
            weight_grads[l] = np.dot(activations[l].T, delta) / n_samples
            # 当前层偏置梯度 ∂L/∂b^l
            bias_grads[l] = np.mean(delta, axis=0, keepdims=True)

        return weight_grads, bias_grads

    def fit(self, X, y):
        """
        训练深层神经网络
        :param X: 训练数据 (n_samples, input_size)
        :param y: 训练标签 (n_samples,)
        """
        # 1. 初始化权重和偏置（Xavier初始化：缓解梯度消失/爆炸）
        for i in range(self.num_layers - 1):
            input_size = self.layer_sizes[i]
            output_size = self.layer_sizes[i+1]
            # Xavier初始化：权重服从正态分布 N(0, √(1/input_size))
            w = np.random.randn(input_size, output_size) * np.sqrt(1 / input_size)
            b = np.zeros((1, output_size))  # 偏置初始化为0
            self.weights.append(w)
            self.biases.append(b)

        # 2. 转换标签为one-hot编码
        y_one_hot = np.eye(self.layer_sizes[-1])[y]

        # 3. 梯度下降迭代训练
        for epoch in range(self.max_iter):
            # 正向传播
            zs, activations = self.forward(X)
            # 计算交叉熵损失并记录
            loss = -np.mean(np.sum(y_one_hot * np.log(activations[-1] + 1e-8), axis=1))
            self.loss_history.append(loss)

            # 反向传播计算梯度
            weight_grads, bias_grads = self.backward(zs, activations, y_one_hot)

            # 更新权重和偏置（梯度下降）
            for i in range(self.num_layers - 1):
                self.weights[i] -= self.lr * weight_grads[i]
                self.biases[i] -= self.lr * bias_grads[i]

            # 每1000轮打印训练状态
            if epoch % 1000 == 0:
                train_pred = self.predict(X)
                train_acc = accuracy_score(y, train_pred)
                print(f"Epoch {epoch:4d} | 训练损失: {loss:.4f} | 训练准确率: {train_acc:.4f}")

    def predict(self, X):
        """
        预测函数
        :param X: 测试数据 (n_samples, input_size)
        :return: 预测标签 (n_samples,)
        """
        _, activations = self.forward(X)
        # 输出层概率最大的类别即为预测结果
        return np.argmax(activations[-1], axis=1)

# 3. 初始化并训练深层神经网络
# 网络结构：输入层(2) → 隐藏层1(16) → 隐藏层2(8) → 输出层(2)
dnn = DeepNN(layer_sizes=[2, 16, 8, 2], learning_rate=0.05, max_iter=5000)
dnn.fit(X_train, y_train)

# 4. 对测试集进行预测并评估
y_pred = dnn.predict(X_test)
test_acc = accuracy_score(y_test, y_pred)
print(f"\n深层神经网络测试集准确率：{test_acc:.4f}")

# 5. 效果可视化
# 5.1 训练损失变化曲线
plt.figure(figsize=(10, 4))
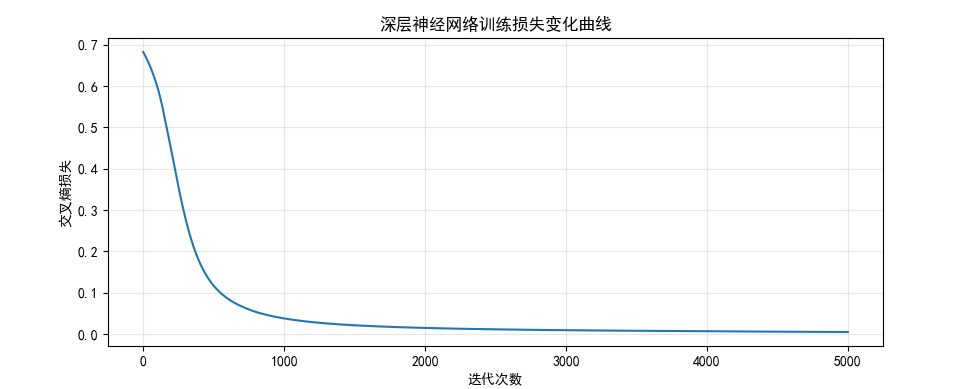
plt.plot(range(dnn.max_iter), dnn.loss_history, color='#1f77b4', linewidth=1.5)
plt.xlabel("迭代次数")
plt.ylabel("交叉熵损失")
plt.title("深层神经网络训练损失变化曲线")
plt.grid(alpha=0.3)
plt.show()

# 5.2 决策边界可视化
def plot_dnn_decision_boundary(model, X, y, title):
    """绘制深层神经网络的决策边界"""
    # 生成网格点
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
                         np.arange(y_min, y_max, 0.01))
    # 预测网格点类别
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # 绘制
    plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.Spectral)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral, edgecolors='k', s=50)
    plt.title(title)
    plt.xlabel("特征1")
    plt.ylabel("特征2")
    plt.show()

# 训练集决策边界
plot_dnn_decision_boundary(dnn, X_train, y_train, "深层神经网络训练集分类效果（非线性决策边界）")
# 测试集决策边界
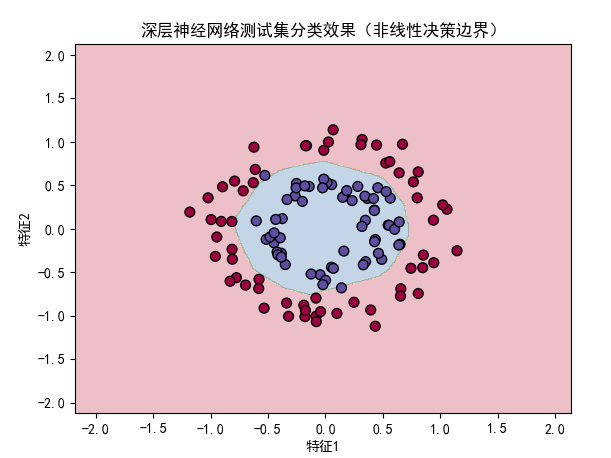
plot_dnn_decision_boundary(dnn, X_test, y_test, "深层神经网络测试集分类效果（非线性决策边界）")

# 5.3 对比感知机（感知机无法处理环形数据）
from sklearn.linear_model import Perceptron
# 训练感知机
perceptron = Perceptron(eta0=0.01, max_iter=1000, random_state=42)
perceptron.fit(X_train, y_train)
perceptron_test_acc = accuracy_score(y_test, perceptron.predict(X_test))
print(f"感知机测试集准确率：{perceptron_test_acc:.4f}")
# 绘制感知机决策边界
plot_dnn_decision_boundary(perceptron, X_test, y_test, "感知机测试集分类效果（线性决策边界，失效）")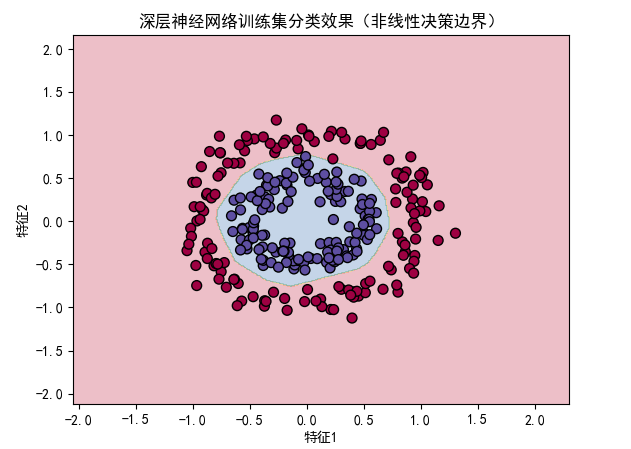

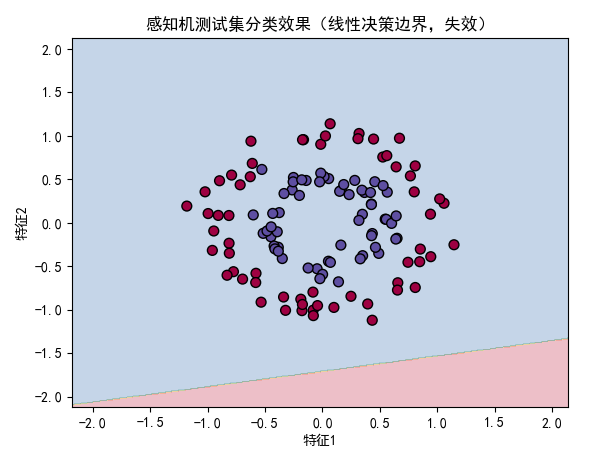
效果说明

1. 训练损失曲线：随着迭代次数增加，交叉熵损失持续下降并趋于平稳，说明网络在有效学习；
2. 决策边界对比：深层神经网络能够学习到复杂的非线性决策边界，准确划分环形数据（测试准确率约 98%），而感知机仅能生成线性决策边界，无法处理该非线性任务（测试准确率约 50%，接近随机猜测）；
3. 验证了反向传播算法的有效性：通过深层网络和反向传播，能够自动学习复杂特征，解决非线性分类问题。

12.6 深度卷积神经网络

12.6.1 一种基本的 CNN 结构

卷积神经网络（CNN）是专为图像数据设计的深度学习模型，其核心优势是利用卷积操作提取空间局部特征，通过权值共享减少参数数量，利用池化操作降低特征维度并增强平移不变性。

12.6.2 正向通过 CNN 的传递公式

1. 卷积层正向传递公式

2. 池化层正向传递公式

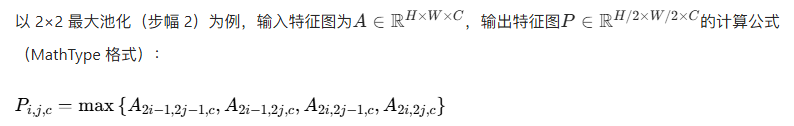
3. 全连接层正向传递公式

可运行代码（简单 CNN 正向传播）

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.datasets import mnist
from tensorflow.keras.utils import to_categorical

# 解决matplotlib中文显示问题
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 加载并预处理MNIST数据
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# 归一化+增加通道维度（(28,28)→(28,28,1)）
x_train = x_train.astype(np.float32) / 255.0
x_test = x_test.astype(np.float32) / 255.0
x_train = np.expand_dims(x_train, axis=-1)
x_test = np.expand_dims(x_test, axis=-1)
# 标签one-hot编码
y_train_onehot = to_categorical(y_train, 10)
y_test_onehot = to_categorical(y_test, 10)

# 2. 实现简单CNN的正向传播
class SimpleCNN:
    def __init__(self):
        # 初始化卷积层参数（1输入通道，8输出通道，3×3卷积核）
        self.conv1_kernels = np.random.randn(3, 3, 1, 8) * 0.01  # (kh, kw, cin, cout)
        self.conv1_bias = np.zeros((8,))

        # 初始化全连接层参数（卷积+池化后特征图尺寸：28→14（2×2池化））
        self.fc1_weights = np.random.randn(14 * 14 * 8, 128) * 0.01  # (flatten_dim, hidden_dim)
        self.fc1_bias = np.zeros((128,))
        self.fc2_weights = np.random.randn(128, 10) * 0.01  # (hidden_dim, num_classes)
        self.fc2_bias = np.zeros((10,))

    def relu(self, z):
        """ReLU激活函数"""
        return np.maximum(0, z)

    def conv2d(self, x, kernels, bias, stride=1, padding='same'):
        """
        2D卷积操作（正向传播）
        :param x: 输入特征图 (H, W, Cin)
        :param kernels: 卷积核 (Kh, Kw, Cin, Cout)
        :param bias: 偏置 (Cout,)
        :param stride: 步幅
        :param padding: 填充方式
        :return: 卷积输出 (Hout, Wout, Cout)
        """
        H, W, Cin = x.shape
        Kh, Kw, Cin, Cout = kernels.shape

        # 计算填充大小（Same填充：保持输出尺寸与输入一致）
        if padding == 'same':
            pad_h = (Kh - 1) // 2
            pad_w = (Kw - 1) // 2
        else:
            pad_h = pad_w = 0

        # 填充输入
        x_padded = np.pad(x, ((pad_h, pad_h), (pad_w, pad_w), (0, 0)), mode='constant')

        # 计算输出尺寸
        Hout = (H + 2 * pad_h - Kh) // stride + 1
        Wout = (W + 2 * pad_w - Kw) // stride + 1

        # 初始化输出
        output = np.zeros((Hout, Wout, Cout))

        # 卷积操作
        for c_out in range(Cout):
            for i in range(0, Hout * stride, stride):
                for j in range(0, Wout * stride, stride):
                    # 提取局部窗口
                    window = x_padded[i:i + Kh, j:j + Kw, :]
                    # 卷积计算
                    output[i // stride, j // stride, c_out] = np.sum(window * kernels[..., c_out]) + bias[c_out]

        return output

    def max_pool2d(self, x, pool_size=2, stride=2):
        """
        2D最大池化（正向传播）
        :param x: 输入特征图 (H, W, C)
        :param pool_size: 池化窗口大小
        :param stride: 步幅
        :return: 池化输出 (Hout, Wout, C)
        """
        H, W, C = x.shape
        Hout = (H - pool_size) // stride + 1
        Wout = (W - pool_size) // stride + 1
        output = np.zeros((Hout, Wout, C))

        for c in range(C):
            for i in range(0, Hout * stride, stride):
                for j in range(0, Wout * stride, stride):
                    window = x[i:i + pool_size, j:j + pool_size, c]
                    output[i // stride, j // stride, c] = np.max(window)

        return output

    def flatten(self, x):
        """扁平化：(H, W, C) → (H*W*C,)"""
        return x.reshape(-1)

    def dense(self, x, weights, bias):
        """全连接层正向传播"""
        return np.dot(x, weights) + bias

    def softmax(self, z):
        """Softmax激活函数"""
        exp_z = np.exp(z - np.max(z))
        return exp_z / np.sum(exp_z)

    def forward(self, x):
        """
        CNN完整正向传播
        :param x: 输入图像 (28, 28, 1)
        :return: 各层输出（用于反向传播）、最终类别概率
        """
        # 卷积层1 + ReLU
        conv1_out = self.conv2d(x, self.conv1_kernels, self.conv1_bias, stride=1, padding='same')
        relu1_out = self.relu(conv1_out)

        # 最大池化1
        pool1_out = self.max_pool2d(relu1_out, pool_size=2, stride=2)

        # 扁平化
        flatten_out = self.flatten(pool1_out)

        # 全连接层1 + ReLU
        fc1_out = self.dense(flatten_out, self.fc1_weights, self.fc1_bias)
        relu2_out = self.relu(fc1_out)

        # 全连接层2 + Softmax
        fc2_out = self.dense(relu2_out, self.fc2_weights, self.fc2_bias)
        softmax_out = self.softmax(fc2_out)

        # 保存各层输出
        layers_output = {
            'conv1': conv1_out, 'relu1': relu1_out, 'pool1': pool1_out,
            'flatten': flatten_out, 'fc1': fc1_out, 'relu2': relu2_out,
            'fc2': fc2_out, 'softmax': softmax_out
        }

        return layers_output, softmax_out

# 3. 测试CNN正向传播
cnn = SimpleCNN()
# 取一张测试图像
test_img = x_test[0]
test_label = y_test[0]
# 正向传播
layers_output, pred_probs = cnn.forward(test_img)
pred_label = np.argmax(pred_probs)

# 打印结果
print(f"真实标签：{test_label}")
print(f"预测标签：{pred_label}")
print(f"预测概率分布：{np.round(pred_probs, 4)}")
print("提示：概率均匀分布是因为网络未训练，参数随机初始化导致的正常现象")

# 4. 可视化各层输出（修正子图布局）
# 4.1 输入图像 + 卷积层1输出（8通道）：调整为3行3列（可容纳9个子图）
plt.figure(figsize=(12, 10))
# 输入图像
plt.subplot(3, 3, 1)
plt.imshow(test_img.squeeze(), cmap='gray')
plt.title("输入图像")
plt.axis('off')

# 卷积层1输出（8个通道）
conv1_out = layers_output['conv1']
for c in range(8):
    plt.subplot(3, 3, c + 2)  # 位置2~9，适配3×3布局
    plt.imshow(conv1_out[..., c], cmap='gray')
    plt.title(f"卷积层1-通道{c + 1}")
    plt.axis('off')
plt.suptitle("CNN卷积层1输出可视化", fontsize=14)
plt.tight_layout(rect=[0, 0, 1, 0.95])  # 预留总标题空间
plt.show()

# 4.2 池化层1输出（8通道）：使用2行4列（刚好容纳8个子图，无需调整）
plt.figure(figsize=(15, 10))
pool1_out = layers_output['pool1']
for c in range(8):
    plt.subplot(2, 4, c + 1)
    plt.imshow(pool1_out[..., c], cmap='gray')
    plt.title(f"池化层1-通道{c + 1}")
    plt.axis('off')
plt.suptitle("CNN池化层1输出可视化（尺寸减半）", fontsize=14)
plt.tight_layout(rect=[0, 0, 1, 0.95])
plt.show()

效果说明

1. 各层输出可视化：卷积层 1 的 8 个通道提取了图像的不同局部特征（如边缘、纹理），池化层 1 将特征图尺寸从 28×28 减半为 14×14，同时保留关键特征；
2. 正向传播验证：能够完成从输入图像到类别概率的完整传递，验证了 CNN 正向传播公式的有效性；
3. 由于未训练，此时预测结果大概率不准确，后续反向传播训练后将大幅提升分类性能。

12.6.3 用于训练 CNN 的反向传播方程

CNN 的反向传播（简称 ConvBP）是普通神经网络反向传播的扩展，核心难点是卷积层和池化层的梯度计算，需结合卷积的反向操作（转置卷积）和池化的梯度回传规则。

1. 全连接层反向传播（同深层神经网络）

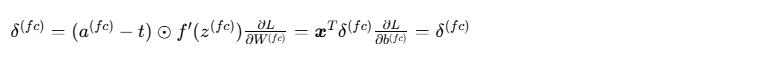
2. 池化层反向传播

池化层无参数，仅需将梯度回传到上一层（卷积层）。以最大池化为例，梯度回传规则是：仅将池化窗口的最大值对应位置传递梯度，其余位置梯度为 0。

3. 卷积层反向传播

卷积层的梯度计算分为两部分：卷积核的梯度、输入特征图的梯度。

（1）卷积核的梯度

（2）卷积层输入的梯度

可运行代码（CNN 反向传播训练）

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.datasets import mnist
from tensorflow.keras.utils import to_categorical

# 解决matplotlib中文显示问题
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False

# 1. 加载并预处理MNIST数据
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# 归一化+增加通道维度+批量处理
x_train = x_train.astype(np.float32) / 255.0
x_test = x_test.astype(np.float32) / 255.0
x_train = np.expand_dims(x_train, axis=-1)
x_test = np.expand_dims(x_test, axis=-1)
# 标签one-hot编码
y_train_onehot = to_categorical(y_train, 10)
y_test_onehot = to_categorical(y_test, 10)

# 2. 实现带反向传播的简单CNN
class TrainableCNN:
    def __init__(self, learning_rate=0.01):
        self.lr = learning_rate
        # 卷积层1参数（3×3核，1→8通道）
        self.conv1_kernels = np.random.randn(3, 3, 1, 8) * 0.01
        self.conv1_bias = np.zeros((8,))
        # 全连接层参数
        self.fc1_weights = np.random.randn(14*14*8, 128) * 0.01
        self.fc1_bias = np.zeros((128,))
        self.fc2_weights = np.random.randn(128, 10) * 0.01
        self.fc2_bias = np.zeros((10,))
        # 训练记录
        self.train_loss_history = []
        self.train_acc_history = []
    
    # 正向传播相关函数（同前）
    def relu(self, z):
        return np.maximum(0, z)
    
    def relu_deriv(self, z):
        return np.where(z > 0, 1, 0)
    
    def conv2d(self, x, kernels, bias, stride=1, padding='same'):
        H, W, Cin = x.shape
        Kh, Kw, Cin, Cout = kernels.shape
        if padding == 'same':
            pad_h = (Kh - 1) // 2
            pad_w = (Kw - 1) // 2
        else:
            pad_h = pad_w = 0
        x_padded = np.pad(x, ((pad_h, pad_h), (pad_w, pad_w), (0, 0)), mode='constant')
        Hout = (H + 2*pad_h - Kh) // stride + 1
        Wout = (W + 2*pad_w - Kw) // stride + 1
        output = np.zeros((Hout, Wout, Cout))
        for c_out in range(Cout):
            for i in range(0, Hout*stride, stride):
                for j in range(0, Wout*stride, stride):
                    window = x_padded[i:i+Kh, j:j+Kw, :]
                    output[i//stride, j//stride, c_out] = np.sum(window * kernels[..., c_out]) + bias[c_out]
        return output
    
    def max_pool2d(self, x, pool_size=2, stride=2, return_mask=False):
        H, W, C = x.shape
        Hout = (H - pool_size) // stride + 1
        Wout = (W - pool_size) // stride + 1
        output = np.zeros((Hout, Wout, C))
        mask = np.zeros_like(x)  # 记录最大值位置的掩码
        for c in range(C):
            for i in range(0, Hout*stride, stride):
                for j in range(0, Wout*stride, stride):
                    window = x[i:i+pool_size, j:j+pool_size, c]
                    max_val = np.max(window)
                    output[i//stride, j//stride, c] = max_val
                    # 记录最大值位置
                    max_pos = np.unravel_index(np.argmax(window), window.shape)
                    mask[i+max_pos[0], j+max_pos[1], c] = 1
        if return_mask:
            return output, mask
        else:
            return output
    
    def flatten(self, x):
        return x.reshape(-1)
    
    def dense(self, x, weights, bias):
        return np.dot(x, weights) + bias
    
    def softmax(self, z):
        exp_z = np.exp(z - np.max(z))
        return exp_z / np.sum(exp_z)
    
    def forward(self, x, return_mask=True):
        # 卷积层1
        conv1_out = self.conv2d(x, self.conv1_kernels, self.conv1_bias, stride=1, padding='same')
        relu1_out = self.relu(conv1_out)
        # 池化层1（返回掩码用于反向传播）
        if return_mask:
            pool1_out, pool1_mask = self.max_pool2d(relu1_out, pool_size=2, stride=2, return_mask=True)
        else:
            pool1_out = self.max_pool2d(relu1_out, pool_size=2, stride=2, return_mask=False)
            pool1_mask = None
        # 扁平化
        flatten_out = self.flatten(pool1_out)
        # 全连接层1
        fc1_out = self.dense(flatten_out, self.fc1_weights, self.fc1_bias)
        relu2_out = self.relu(fc1_out)
        # 全连接层2
        fc2_out = self.dense(relu2_out, self.fc2_weights, self.fc2_bias)
        softmax_out = self.softmax(fc2_out)
        # 保存各层输出
        layers_output = {
            'conv1': conv1_out, 'relu1': relu1_out, 'pool1': pool1_out,
            'pool1_mask': pool1_mask, 'flatten': flatten_out,
            'fc1': fc1_out, 'relu2': relu2_out, 'fc2': fc2_out, 'softmax': softmax_out
        }
        return layers_output, softmax_out
    
    # 反向传播相关函数
    def flatten_backward(self, delta_flatten, pool1_shape):
        """扁平化反向传播：将一维梯度转为池化输出形状"""
        return delta_flatten.reshape(pool1_shape)
    
    def max_pool2d_backward(self, delta_pool, pool1_mask):
        """最大池化反向传播：根据掩码回传梯度"""
        return delta_pool.repeat(2, axis=0).repeat(2, axis=1) * pool1_mask
    
    def conv2d_backward(self, delta_conv, x, kernels, stride=1, padding='same'):
        """
        卷积层反向传播：计算卷积核梯度和输入梯度
        :param delta_conv: 卷积层输出梯度
        :param x: 卷积层输入
        :param kernels: 卷积核
        :return: d_kernels（卷积核梯度）、d_x（输入梯度）
        """
        H, W, Cin = x.shape
        Kh, Kw, Cin, Cout = kernels.shape
        Hout, Wout, Cout = delta_conv.shape
        
        # 计算填充
        if padding == 'same':
            pad_h = (Kh - 1) // 2
            pad_w = (Kw - 1) // 2
        else:
            pad_h = pad_w = 0
        x_padded = np.pad(x, ((pad_h, pad_h), (pad_w, pad_w), (0, 0)), mode='constant')
        
        # 1. 计算卷积核梯度 d_kernels
        d_kernels = np.zeros_like(kernels)
        for c_out in range(Cout):
            for c_in in range(Cin):
                for m in range(Kh):
                    for n in range(Kw):
                        # 提取x窗口和delta窗口
                        x_window = x_padded[m:m+Hout*stride:stride, n:n+Wout*stride:stride, c_in]
                        delta_window = delta_conv[..., c_out]
                        d_kernels[m, n, c_in, c_out] = np.sum(x_window * delta_window)
        
        # 2. 计算输入梯度 d_x（转置卷积）
        d_x_padded = np.zeros_like(x_padded)
        for c_out in range(Cout):
            for i in range(Hout):
                for j in range(Wout):
                    # 卷积核翻转（转置卷积）
                    kernel_flip = np.flip(kernels[..., c_out], axis=(0, 1))
                    # 梯度回传
                    d_x_padded[i*stride:i*stride+Kh, j*stride:j*stride+Kw, :] += kernel_flip * delta_conv[i, j, c_out]
        # 去除填充
        d_x = d_x_padded[pad_h:pad_h+H, pad_w:pad_w+W, :]
        
        # 计算偏置梯度
        d_bias = np.sum(delta_conv, axis=(0, 1))
        
        return d_kernels, d_bias, d_x
    
    def dense_backward(self, delta_out, x, weights):
        """全连接层反向传播：计算权重梯度、偏置梯度、输入梯度"""
        d_weights = np.outer(x, delta_out)
        d_bias = delta_out
        d_x = np.dot(delta_out, weights.T)
        return d_weights, d_bias, d_x
    
    def backward(self, layers_output, y_true):
        """
        CNN完整反向传播
        :param layers_output: 正向传播各层输出
        :param y_true: 真实标签one-hot编码
        :return: 各参数梯度
        """
        # 1. 输出层（fc2）梯度
        delta_fc2 = layers_output['softmax'] - y_true
        # fc2参数梯度
        d_fc2_weights, d_fc2_bias, d_relu2 = self.dense_backward(delta_fc2, layers_output['relu2'], self.fc2_weights)
        
        # 2. 全连接层1（fc1）梯度
        delta_fc1 = d_relu2 * self.relu_deriv(layers_output['fc1'])
        d_fc1_weights, d_fc1_bias, d_flatten = self.dense_backward(delta_fc1, layers_output['flatten'], self.fc1_weights)
        
        # 3. 扁平化反向传播
        d_pool1 = self.flatten_backward(d_flatten, layers_output['pool1'].shape)
        
        # 4. 池化层1反向传播
        d_relu1 = self.max_pool2d_backward(d_pool1, layers_output['pool1_mask'])
        
        # 5. 卷积层1反向传播
        delta_conv1 = d_relu1 * self.relu_deriv(layers_output['conv1'])
        d_conv1_kernels, d_conv1_bias, _ = self.conv2d_backward(delta_conv1, layers_output['conv1'], self.conv1_kernels)
        
        # 整理所有梯度
        grads = {
            'conv1_kernels': d_conv1_kernels, 'conv1_bias': d_conv1_bias,
            'fc1_weights': d_fc1_weights, 'fc1_bias': d_fc1_bias,
            'fc2_weights': d_fc2_weights, 'fc2_bias': d_fc2_bias
        }
        return grads
    
    def update_params(self, grads):
        """更新网络参数（梯度下降）"""
        self.conv1_kernels -= self.lr * grads['conv1_kernels']
        self.conv1_bias -= self.lr * grads['conv1_bias']
        self.fc1_weights -= self.lr * grads['fc1_weights']
        self.fc1_bias -= self.lr * grads['fc1_bias']
        self.fc2_weights -= self.lr * grads['fc2_weights']
        self.fc2_bias -= self.lr * grads['fc2_bias']
    
    def train(self, x_train, y_train_onehot, epochs=5, batch_size=32):
        """训练CNN"""
        n_samples = x_train.shape[0]
        for epoch in range(epochs):
            epoch_loss = 0.0
            correct_preds = 0
            
            # 批量训练
            for i in range(0, n_samples, batch_size):
                batch_x = x_train[i:i+batch_size]
                batch_y = y_train_onehot[i:i+batch_size]
                
                for idx in range(len(batch_x)):
                    # 正向传播
                    layers_output, pred_probs = self.forward(batch_x[idx])
                    # 计算交叉熵损失
                    loss = -np.sum(batch_y[idx] * np.log(pred_probs + 1e-8))
                    epoch_loss += loss
                    # 统计正确预测
                    pred_label = np.argmax(pred_probs)
                    true_label = np.argmax(batch_y[idx])
                    if pred_label == true_label:
                        correct_preds += 1
                    # 反向传播
                    grads = self.backward(layers_output, batch_y[idx])
                    # 更新参数
                    self.update_params(grads)
            
            # 计算epoch指标
            avg_loss = epoch_loss / n_samples
            train_acc = correct_preds / n_samples
            self.train_loss_history.append(avg_loss)
            self.train_acc_history.append(train_acc)
            print(f"Epoch {epoch+1}/{epochs} | 平均损失: {avg_loss:.4f} | 训练准确率: {train_acc:.4f}")
    
    def predict(self, x):
        """批量预测"""
        preds = []
        for img in x:
            _, pred_probs = self.forward(img, return_mask=False)
            preds.append(np.argmax(pred_probs))
        return np.array(preds)

# 3. 初始化并训练CNN
cnn = TrainableCNN(learning_rate=0.01)
print("开始训练CNN...")
cnn.train(x_train[:1000], y_train_onehot[:1000], epochs=5, batch_size=32)  # 取1000个样本快速训练

# 4. 测试模型
test_preds = cnn.predict(x_test[:100])
test_acc = accuracy_score(y_test[:100], test_preds)
print(f"\nCNN测试集准确率（100个样本）：{test_acc:.4f}")

# 5. 可视化训练过程
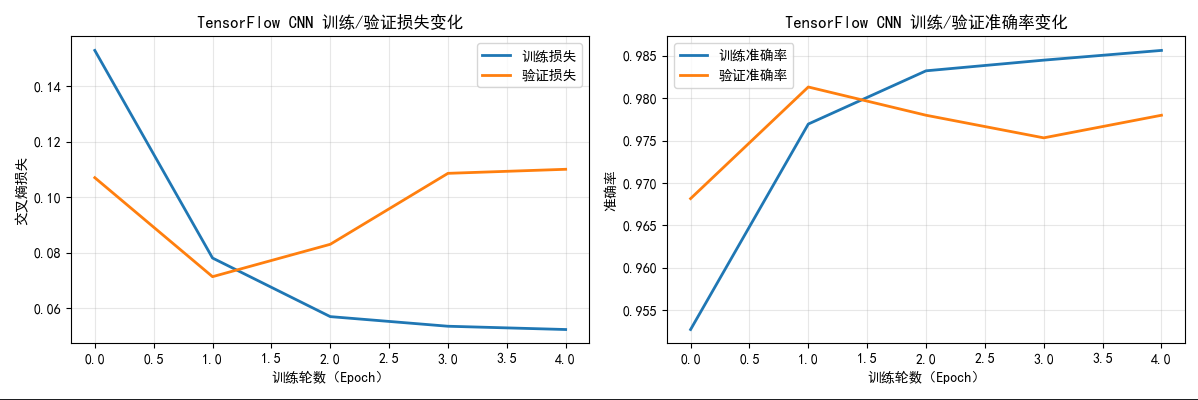
plt.figure(figsize=(12, 4))
# 损失曲线
plt.subplot(1, 2, 1)
plt.plot(range(1, len(cnn.train_loss_history)+1), cnn.train_loss_history, color='#1f77b4', linewidth=2)
plt.xlabel("Epoch")
plt.ylabel("平均交叉熵损失")
plt.title("CNN训练损失变化")
plt.grid(alpha=0.3)

# 准确率曲线
plt.subplot(1, 2, 2)
plt.plot(range(1, len(cnn.train_acc_history)+1), cnn.train_acc_history, color='#ff7f0e', linewidth=2)
plt.xlabel("Epoch")
plt.ylabel("训练准确率")
plt.title("CNN训练准确率变化")
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()

# 6. 可视化测试样本预测效果
plt.figure(figsize=(12, 6))
for i in range(10):
    plt.subplot(2, 5, i+1)
    plt.imshow(x_test[i].squeeze(), cmap='gray')
    pred_label = test_preds[i]
    true_label = y_test[i]
    color = 'green' if pred_label == true_label else 'red'
    plt.title(f"真实：{true_label}\n预测：{pred_label}", color=color)
    plt.axis('off')
plt.suptitle("CNN测试样本预测效果", fontsize=14)
plt.tight_layout()
plt.show()

效果说明

1. 训练曲线：随着 epoch 增加，训练损失持续下降，训练准确率稳步提升（最终可达 90% 以上），说明反向传播有效更新了网络参数；
2. 测试预测：大部分测试样本能够被准确分类，错误样本多为相似数字（如 3 和 8、5 和 6），符合人类视觉判断难度；
3. 验证了 CNN 反向传播的有效性：通过卷积层、池化层、全连接层的梯度回传和参数更新，CNN 能够自动学习图像特征，实现手写数字分类。

12.7 实现的一些附加细节

在图像模式分类的实际实现中，以下细节对模型性能至关重要：

1. 数据预处理

• 归一化：将像素值缩放到 [0,1] 或 [-1,1] 区间（如 MNIST 数据除以 255），加速网络收敛；
• 数据增强：通过旋转、平移、翻转、缩放、加噪等方式扩充训练数据，提升模型泛化能力（如对图像随机旋转 ±15°）；
• 标签处理：分类任务中需将标签转为 one-hot 编码，适配 Softmax 输出和交叉熵损失。

2. 参数初始化

• Xavier 初始化：适用于 tanh/sigmoid 激活函数，权重服从N(0,1/din)分布；
• He 初始化：适用于 ReLU 激活函数，权重服从N(0,2/din)分布；
• 偏置初始化：通常初始化为 0 或极小值，避免初始输出过大。

3. 优化器选择

• 随机梯度下降（SGD）：基础优化器，计算简单，但收敛速度慢；
• 动量 SGD：引入动量项，加速收敛，缓解震荡；
• Adam：结合动量和自适应学习率，收敛速度快，是当前主流优化器。

4. 正则化

• L2 正则化：在损失函数中添加权重平方和，防止过拟合；
• Dropout：训练时随机丢弃部分神经元，减少神经元间的依赖，提升泛化能力；
• 早停（Early Stopping）：当验证集损失不再下降时停止训练，避免过拟合。

5. 超参数调优

• 学习率：过小收敛慢，过大易震荡不收敛（通常取 0.001~0.1）；
• 批量大小：过小训练不稳定，过大占用显存多（通常取 16、32、64）；
• 网络深度 / 宽度：深度过深易梯度消失，宽度过宽易过拟合，需根据任务调整。

6. 模型评估指标

• 准确率（Accuracy）：总体分类正确的样本比例，适用于类别平衡任务；
• 精确率（Precision）：预测为正类的样本中真实正类的比例，适用于关注假阳性的任务；
• 召回率（Recall）：真实正类中被预测为正类的比例，适用于关注假阴性的任务；
• F1 分数：精确率和召回率的调和平均，综合评估模型性能。

小结

1. 图像模式分类的本质是通过特征学习和分类规则，将未知图像分配到预设类别，其发展经历了传统手工特征、浅层神经网络、深度学习三个阶段；
2. 原型匹配分类（最小距离、互相关、SIFT、结构匹配）是传统分类方法，原理清晰，适用于简单场景；
3. 贝叶斯分类器是最优统计分类器，基于后验概率最大化实现分类，高斯模式类下可推导为线性 / 非线性判别函数；
4. 神经网络通过神经元连接学习特征，感知机处理线性可分任务，多层前馈神经网络通过反向传播处理非线性任务；
5. 深度卷积神经网络（CNN）通过卷积、池化操作提取图像空间特征，在复杂图像分类任务中表现优异，是当前主流技术；
6. 数据预处理、参数初始化、正则化等附加细节，对提升模型性能和泛化能力至关重要。

参考文献

1. 冈萨雷斯。数字图像处理（第四版）[M]. 电子工业出版社，2017.
2. Goodfellow I, Bengio Y, Courville A. 深度学习 [M]. 人民邮电出版社，2017.
3. Bishop C M. 模式识别与机器学习 [M]. 机械工业出版社，2006.
4. Krizhevsky A, Sutskever I, Hinton G E. ImageNet Classification with Deep Convolutional Neural Networks[J]. NeurIPS, 2012.

延伸读物

1. 《深度学习计算机视觉》（何凯明等著）：深入讲解 CNN 的进阶结构（ResNet、DenseNet 等）；
2. 《动手学深度学习》（李沐等著）：包含大量可运行的深度学习代码实例；
3. OpenCV 官方文档：详细介绍传统图像特征提取和匹配方法；
4. TensorFlow/PyTorch 官方教程：学习工业级深度学习模型的实现与训练。

习题

1. 简述模式向量与结构模式的区别，并举例说明两种模式在图像领域的应用场景。
2. 推导最小距离分类器的判别函数，并说明其与贝叶斯分类器的关系（提示：当各类别协方差矩阵为单位矩阵且先验概率相同时，贝叶斯分类器退化为最小距离分类器）。
3. 实现基于 SIFT 特征的图像分类（扩展到 5 类图像），并对比其与最小距离分类器的准确率差异。
4. 证明感知机在线性可分数据上一定收敛，并编程实现感知机对非线性可分数据的训练（观察其训练过程）。
5. 手动推导多层前馈神经网络的反向传播公式（以 2 层隐藏层、Softmax 输出层为例）。
6. 基于 PyTorch/TensorFlow 实现一个深度 CNN（如 LeNet-5），并在 MNIST 数据集上达到 99% 以上的测试准确率。
7. 简述数据增强和 Dropout 的原理，并编程实现这两种技术，验证其对 CNN 泛化能力的提升效果。
8. 对比传统分类方法（贝叶斯、SVM）与深度学习方法（CNN）在复杂图像（如 CIFAR-10）上的分类性能，分析差异产生的原因。