蒙特卡洛方法(Monte Carlo Method)
一、蒙特卡洛方法简介
1.1 历史背景
想象你置身于摩纳哥的蒙特卡洛赌场,轮盘转动、骰子翻滚,每一局结果充满随机性。
20世纪40年代,美国"曼哈顿计划"的科学家乌拉姆(S.M. Ulam)和冯·诺伊曼(John von Neumann)却从赌城的随机游戏中获得灵感,开创了一种用随机数解决确定性难题的计算方法------蒙特卡洛方法(Monte Carlo Method)。
1.2 基本定义
蒙特卡洛方法 (Monte Carlo method)也被称为统计模拟方法,是一种基于概率统计的数值计算方法。
核心思想:
- 不断抽样 - 通过大量随机采样收集数据
- 逐渐逼近 - 随着采样次数增加,估计值越来越接近真实值
采样方法:
-
直接采样
- 在已知分布函数的情况下,随机抽样得到对应样本。例如,按转移概率采样下一个状态
-
接受-拒绝采样
- 在分布函数P(x)P(x)P(x)不好直接采样的情况下,定义一个提议分布q(x)q(x)q(x),并满足p(x)≤Mq(x),∀xp(x)≤Mq(x),∀xp(x)≤Mq(x),∀x
并按照以下步骤进行采样:- 从提议分布 q(x)q(x)q(x)进行直接采样
- 从u∼Uniform(0,1)u∼Uniform(0,1)u∼Uniform(0,1)进行采样
若 u≤p(x)Mq(x)u≤\frac{p(x)}{Mq(x)}u≤Mq(x)p(x),则接受采样否侧拒绝采样
其几何意义为 用kq(x)kq(x)kq(x)包裹住目标分布,并在内部随机撒点,在目标分布P(x)P(x)P(x)里面的才会被留下
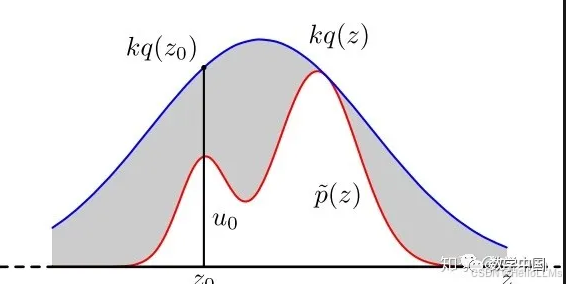
- 在分布函数P(x)P(x)P(x)不好直接采样的情况下,定义一个提议分布q(x)q(x)q(x),并满足p(x)≤Mq(x),∀xp(x)≤Mq(x),∀xp(x)≤Mq(x),∀x
-
重要性采样
- 接受拒绝采样完美的解决了累积分布函数不可求时的采样问题。但是接受拒绝采样非常依赖于提议分布(proposal distribution)的选择,如果提议分布选择的不好,可能采样时间很长却获得很少满足分布的粒子。
而重要性采样就解决了这一问题。直接采样与接受拒绝采样都是假设每个粒子的权重相等,而重要性采样则是给予每个粒子不同的权重,使用加权平均的方法来计算期望:Ep[f(x)]=Eq[f(x)p(x)q(x)]E_p[f(x)]=E_q[f(x)\frac{p(x)}{q(x)}]Ep[f(x)]=Eq[f(x)q(x)p(x)]
具体步骤为:- 从提议分布 q(x)q(x)q(x) 采样
- 给每个样本一个权重 w=p(x)q(x)w = \frac{p(x)}{q(x)}w=q(x)p(x)
- 求期望 Ep[f(x)]=Eq[f(x)p(x)q(x)]=1NΣf(xi)p(x)q(x)E_p[f(x)]=E_q[f(x)\frac{p(x)}{q(x)}] = \frac{1}{N}\Sigma f(x_i) \frac{p(x)}{q(x)}Ep[f(x)]=Eq[f(x)q(x)p(x)]=N1Σf(xi)q(x)p(x)
- 接受拒绝采样完美的解决了累积分布函数不可求时的采样问题。但是接受拒绝采样非常依赖于提议分布(proposal distribution)的选择,如果提议分布选择的不好,可能采样时间很长却获得很少满足分布的粒子。
python
import numpy as np
from scipy.stats import norm, uniform
# 目标分布
def p(x):
return 0.3*np.exp(-(x-0.3)**2) + 0.7*np.exp(-(x-2.)**2/0.3)
# 建议分布: N(1.4, 1.2)
G_rv = norm(loc=1.4, scale=1.2)
C = 2.5
uniform_rv = uniform(loc=0, scale=1)
sample = []
for i in range(10000):
Y = G_rv.rvs(1)[0] # 从建议分布采样
U = uniform_rv.rvs(1)[0] # 从均匀分布采样
if p(Y) >= U * C * G_rv.pdf(Y):
sample.append(Y) # 接受样本1.3 示例
示例1: 估计圆周率π
如下图所示,在一个正方形内部随机产生若干个点,细数落在圆中的点的个数,圆的面积与正方形的面积之比就等于圆中点的个数与正方形中点的个数之比。
设圆的半径为r=1,则:
- 圆的面积 = π
- 正方形面积 = 4
- 圆的面积/正方形面积 = π/4
因此: π ≈ 4 × (圆内点数/总点数)
python
import random
total = [10, 100, 1000, 10000, 100000, 1000000, 5000000]
for t in total:
in_count = 0
for i in range(t):
x = random.random()
y = random.random()
dis = (x**2 + y**2)**0.5
if dis <= 1:
in_count += 1
print(f'{t}个随机点时,π是: {4*in_count/t}')随机点数越多,估计值越接近真实的π值。
示例2: 计算不规则图形面积
对于不规则图形,可以通过向图上随机打点,然后获取像素点所在的颜色来计算面积:
白色面积 = (白色点数/总点数) × 图片总面积
python
from PIL import Image
import random
img = Image.open('monte.png')
total = [10, 100, 1000, 10000, 100000, 1000000, 5000000]
for t in total:
in_count = 0
for i in range(t):
x = random.randint(0, img.width-1)
y = random.randint(0, img.height-1)
if img.getpixel((x,y)) == (255,255,255,255):
in_count += 1
print(f'{t}个随机点时,白色面积为: {int(img.width*img.height*in_count/t)}')二、蒙特卡洛方法在强化学习中的应用
2.1 强化学习背景
在强化学习中,我们需要估计策略的价值函数。蒙特卡洛方法提供了一种无需环境模型的价值函数估计方法。
2.2 蒙特卡洛方法估计状态价值
2.2.1 基本原理
一个状态的价值是它的期望回报,因此我们可以:
- 用策略在MDP上采样很多条序列
- 计算从这个状态出发的回报
- 求这些回报的期望
公式表示:
Vπ(s)=Eτ∼π[Gt∣st=s]≈1N(s)∑i=1N(s)Gt(i)V^{\pi}(s) = \mathbb{E}{\tau \sim \pi}[G_t | s_t = s] \approx \frac{1}{N(s)} \sum{i=1}^{N(s)} G_t^{(i)}Vπ(s)=Eτ∼π[Gt∣st=s]≈N(s)1i=1∑N(s)Gt(i)
其中:
- Vπ(s)V^{\pi}(s)Vπ(s) 是状态s在策略π下的价值
- GtG_tGt 是从时刻t开始的回报
- N(s)N(s)N(s) 是状态s被访问的次数
2.2.2 算法步骤
第一步: 使用策略π采样若干条序列:
s0→a0r0→s1→a1r1→s2→a2⋯→rT−1→sTs_0 \xrightarrow{a_0} r_0 \rightarrow s_1 \xrightarrow{a_1} r_1 \rightarrow s_2 \xrightarrow{a_2} \cdots \xrightarrow{} r_{T-1} \rightarrow s_Ts0a0 r0→s1a1 r1→s2a2 ⋯ rT−1→sT
第二步: 对每一条序列中的每一时间步t的状态s进行以下操作:
- 更新状态s的计数器: N(s)←N(s)+1N(s) \leftarrow N(s) + 1N(s)←N(s)+1
- 更新状态s的总回报: M(s)←M(s)+GtM(s) \leftarrow M(s) + G_tM(s)←M(s)+Gt
- 估计状态价值: V(s)=M(s)/N(s)V(s) = M(s) / N(s)V(s)=M(s)/N(s)
根据大数定律,当 N(s)→∞N(s) \rightarrow \inftyN(s)→∞ 时,有 V(s)→Vπ(s)V(s) \rightarrow V^{\pi}(s)V(s)→Vπ(s)
2.2.3 增量更新方法
除了累加所有回报再求平均,还可以使用增量更新:
V(s)←V(s)+1N(s)[G−V(s)]V(s) \leftarrow V(s) + \frac{1}{N(s)}[G - V(s)]V(s)←V(s)+N(s)1[G−V(s)]
这种方法可以大幅降低计算复杂度。