神经网络的正向传播和反向传播 包括可视化源码

神经网络的正向传播和反向传播 包括可视化源码

flyfish

二层神经网络（1隐藏层+1输出层）

网络结构 ：输入层（无参数）→ 隐藏层（参数w1,b1w_1,b_1w1,b1）→ 输出层（参数w2,b2w_2,b_2w2,b2）
激活函数 ：sigmoid函数σ(t)=11+e−t\sigma(t) = \frac{1}{1+e^{-t}}σ(t)=1+e−t1，导数特性σ′(t)=σ(t)(1−σ(t))\sigma'(t) = \sigma(t)(1-\sigma(t))σ′(t)=σ(t)(1−σ(t))（简化计算）
中间变量定义：

1. 隐藏层加权和：z1=w1x+b1z_1 = w_1 x + b_1z1=w1x+b1（输入x经权重偏置线性变换）
2. 隐藏层激活输出：a1=σ(z1)a_1 = \sigma(z_1)a1=σ(z1)（线性结果经非线性激活）
3. 输出层加权和：z2=w2a1+b2z_2 = w_2 a_1 + b_2z2=w2a1+b2（隐藏层输出经权重偏置线性变换）
4. 最终预测值：o=σ(z2)o = \sigma(z_2)o=σ(z2)（输出层线性结果经激活得到预测）

损失函数 ：均方误差（MSE）L=12(t−o)2L = \frac{1}{2}(t - o)^2L=21(t−o)2，其中ttt为真实标签（已知）

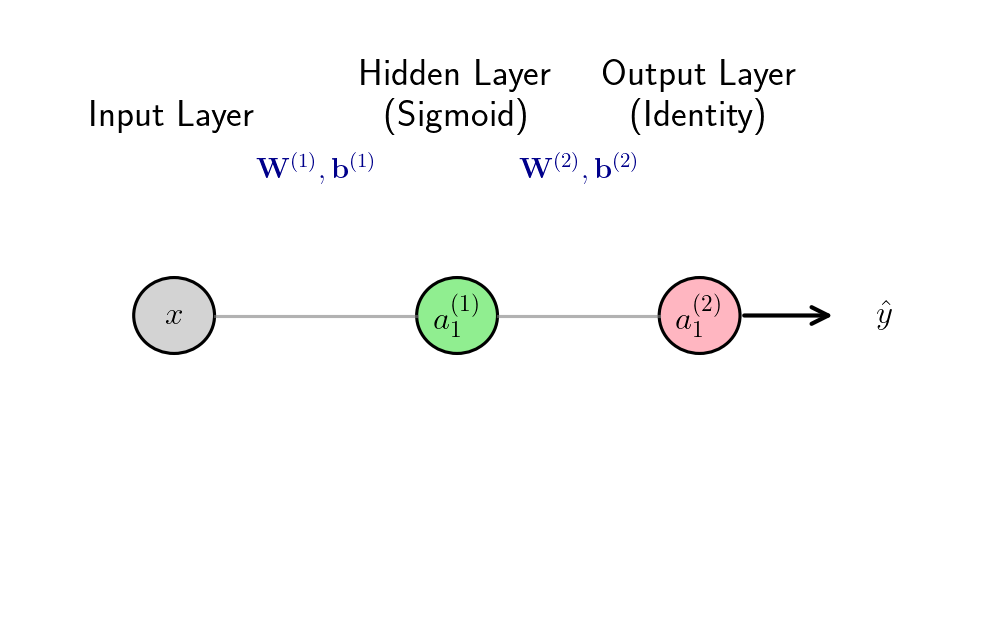绘图源码在文末

o=σ2(w2⋅σ1(w1x+b1)+b2) o = \sigma_2\left( w_2 \cdot \sigma_1\left( w_1 x + b_1 \right) + b_2 \right) o=σ2(w2⋅σ1(w1x+b1)+b2)

1. 第一层（输入→隐藏层激活输出） ：隐藏层是线性函数+激活函数的复合
   a1=σ1(f1(x))其中f1(x)=w1x+b1 a_1 = \sigma_1\left( f_1(x) \right) \quad \text{其中} \quad f_1(x) = w_1 x + b_1 a1=σ1(f1(x))其中f1(x)=w1x+b1
   f1(x)f_1(x)f1(x)：线性变换函数（加权和）；
   σ1(⋅)\sigma_1(\cdot)σ1(⋅)：非线性激活函数（如sigmoid），将线性结果映射到非线性空间。

2. 第二层（隐藏层→输出层预测值） ：输出层是线性函数+激活函数的复合，且输入为第一层的输出 a1a_1a1
   o=σ2(f2(a1))其中f2(a1)=w2a1+b2 o = \sigma_2\left( f_2(a_1) \right) \quad \text{其中} \quad f_2(a_1) = w_2 a_1 + b_2 o=σ2(f2(a1))其中f2(a1)=w2a1+b2
   f2(a1)f_2(a_1)f2(a1)：输出层的线性变换函数；
   σ2(⋅)\sigma_2(\cdot)σ2(⋅)：输出层激活函数（回归任务用恒等函数 σ2(z)=z\sigma_2(z)=zσ2(z)=z，二分类用sigmoid，多分类用softmax）。

3. 复合函数 ：将 a1=σ1(w1x+b1)a_1 = \sigma_1(w_1 x + b_1)a1=σ1(w1x+b1) 代入 f2(a1)f_2(a_1)f2(a1)，得到最终的嵌套表达式：
   o=σ2(w2⋅σ1(w1x+b1)+b2) o = \sigma_2\left( w_2 \cdot \sigma_1\left( w_1 x + b_1 \right) + b_2 \right) o=σ2(w2⋅σ1(w1x+b1)+b2)

一、正向传播（Forward Propagation）

从输入x出发，逐层计算中间变量，最终得到预测值o和损失L，为反向传播提供缓存数据。
x→z1=w1x+b1z1→a1=σ(z1)a1→z2=w2a1+b2z2→o=σ(z2)o→L=12(t−o)2L x \xrightarrow{z_1=w_1x+b_1} z_1 \xrightarrow{a_1=\sigma(z_1)} a_1 \xrightarrow{z_2=w_2a_1+b_2} z_2 \xrightarrow{o=\sigma(z_2)} o \xrightarrow{L=\frac{1}{2}(t-o)^2} L xz1=w1x+b1 z1a1=σ(z1) a1z2=w2a1+b2 z2o=σ(z2) oL=21(t−o)2 L

步骤1：计算隐藏层中间变量

1.1 隐藏层加权和（线性变换）

z1=w1x+b1z_1 = w_1 x + b_1z1=w1x+b1

输入x通过权重w1w_1w1缩放、偏置b1b_1b1平移，得到线性组合结果，对应加法节点+乘法节点的组合计算。

1.2 隐藏层激活输出（非线性变换）

a1=σ(z1)=11+e−z1a_1 = \sigma(z_1) = \frac{1}{1+e^{-z_1}}a1=σ(z1)=1+e−z11

通过sigmoid激活函数，将线性结果z1z_1z1映射到(0,1)区间，引入非线性，让网络能拟合复杂关系。

步骤2：计算输出层中间变量

2.1 输出层加权和（线性变换）

z2=w2a1+b2z_2 = w_2 a_1 + b_2z2=w2a1+b2

隐藏层输出a1a_1a1作为输入，经输出层权重w2w_2w2、偏置b2b_2b2线性变换，得到输出层的线性结果。

2.2 最终预测值（非线性变换）

o=σ(z2)=11+e−z2o = \sigma(z_2) = \frac{1}{1+e^{-z_2}}o=σ(z2)=1+e−z21

输出层线性结果经sigmoid激活，得到最终预测值，适用于二分类或回归场景（此处以回归为例）。

步骤3：计算损失函数（误差量化）

L=12(t−o)2L = \frac{1}{2}(t - o)^2L=21(t−o)2

将真实值ttt与预测值ooo的差距（原始误差e=t−oe=t-oe=t−o）平方后乘以1/2，目的是让后续求导时系数更简洁，同时量化模型预测的误差大小。

二、反向传播（Backward Propagation）

从损失L出发，利用链式法则逐层反向计算每个参数的梯度（∂L∂w1、∂L∂b1、∂L∂w2、∂L∂b2\frac{\partial L}{\partial w_1}、\frac{\partial L}{\partial b_1}、\frac{\partial L}{\partial w_2}、\frac{\partial L}{\partial b_2}∂w1∂L、∂b1∂L、∂w2∂L、∂b2∂L），为梯度下降提供参数更新的依据。

L→δ2=−(t−o)o(1−o)δ2→∂L∂w2=δ2a1,∂L∂b2=δ2w2,b2梯度→δ1=δ2w2a1(1−a1)δ1→∂L∂w1=δ1x,∂L∂b1=δ1w1,b1梯度 L \xrightarrow{\delta_2=-(t-o)o(1-o)} \delta_2 \xrightarrow{\frac{\partial L}{\partial w_2}=\delta_2a_1, \frac{\partial L}{\partial b_2}=\delta_2} w_2,b_2梯度 \xrightarrow{\delta_1=\delta_2w_2a_1(1-a_1)} \delta_1 \xrightarrow{\frac{\partial L}{\partial w_1}=\delta_1x, \frac{\partial L}{\partial b_1}=\delta_1} w_1,b_1梯度 Lδ2=−(t−o)o(1−o) δ2∂w2∂L=δ2a1,∂b2∂L=δ2 w2,b2梯度δ1=δ2w2a1(1−a1) δ1∂w1∂L=δ1x,∂b1∂L=δ1 w1,b1梯度

步骤1：计算输出层误差梯度δ2\delta_2δ2（损失对输出层加权和的偏导）

原始展开式（链式法则）

δ2=∂L∂z2=∂L∂o⋅∂o∂z2\delta_2 = \frac{\partial L}{\partial z_2} = \frac{\partial L}{\partial o} \cdot \frac{\partial o}{\partial z_2}δ2=∂z2∂L=∂o∂L⋅∂z2∂o

损失L对z2z_2z2的梯度，等于损失对预测值o的梯度，乘以预测值o对z2z_2z2的梯度（链式法则的"传递"逻辑）。

代入各局部导数

1. 损失对预测值的梯度：∂L∂o=∂∂o[12(t−o)2]=−(t−o)\frac{\partial L}{\partial o} = \frac{\partial}{\partial o}\left[\frac{1}{2}(t-o)^2\right] = -(t - o)∂o∂L=∂o∂[21(t−o)2]=−(t−o)（对MSE损失求导，幂函数求导法则）；
2. 预测值对输出层加权和的梯度：∂o∂z2=σ′(z2)=o(1−o)\frac{\partial o}{\partial z_2} = \sigma'(z_2) = o(1 - o)∂z2∂o=σ′(z2)=o(1−o)（sigmoid激活函数的导数特性）。

简化合并项

δ2=−(t−o)⋅o(1−o)\delta_2 = -(t - o) \cdot o(1 - o)δ2=−(t−o)⋅o(1−o)
δ2\delta_2δ2是输出层的 误差梯度 ，代表损失L随输出层加权和z2z_2z2变化的速率，是后续计算输出层参数梯度的核心中间量。

步骤2：计算输出层参数（w2、b2w_2、b_2w2、b2）的梯度

2.1 输出层权重w2w_2w2的梯度

原始展开式（链式法则）

∂L∂w2=∂L∂z2⋅∂z2∂w2\frac{\partial L}{\partial w_2} = \frac{\partial L}{\partial z_2} \cdot \frac{\partial z_2}{\partial w_2}∂w2∂L=∂z2∂L⋅∂w2∂z2

损失L对w2w_2w2的梯度，等于损失对z2z_2z2的梯度（即δ2\delta_2δ2），乘以z2z_2z2对w2w_2w2的梯度。

代入各局部导数

1. 损失对z2z_2z2的梯度：∂L∂z2=δ2\frac{\partial L}{\partial z_2} = \delta_2∂z2∂L=δ2（已在步骤1算出，直接复用）；
2. z2z_2z2对w2w_2w2的梯度：∂z2∂w2=a1\frac{\partial z_2}{\partial w_2} = a_1∂w2∂z2=a1（z2=w2a1+b2z_2 = w_2a_1 + b_2z2=w2a1+b2，对w2w_2w2求导，乘法节点特性：固定a1a_1a1，导数为a1a_1a1）。

简化合并项

∂L∂w2=δ2⋅a1\frac{\partial L}{\partial w_2} = \delta_2 \cdot a_1∂w2∂L=δ2⋅a1

2.2 输出层偏置b2b_2b2的梯度

原始展开式（链式法则）

∂L∂b2=∂L∂z2⋅∂z2∂b2\frac{\partial L}{\partial b_2} = \frac{\partial L}{\partial z_2} \cdot \frac{\partial z_2}{\partial b_2}∂b2∂L=∂z2∂L⋅∂b2∂z2

损失L对b2b_2b2的梯度，等于损失对z2z_2z2的梯度，乘以z2z_2z2对b2b_2b2的梯度。

代入各局部导数

1. 损失对z2z_2z2的梯度：∂L∂z2=δ2\frac{\partial L}{\partial z_2} = \delta_2∂z2∂L=δ2（复用步骤1的结果）；
2. z2z_2z2对b2b_2b2的梯度：∂z2∂b2=1\frac{\partial z_2}{\partial b_2} = 1∂b2∂z2=1（z2=w2a1+b2z_2 = w_2a_1 + b_2z2=w2a1+b2，对b2b_2b2求导，加法节点特性：固定其他项，导数为1）。

简化合并项

∂L∂b2=δ2\frac{\partial L}{\partial b_2} = \delta_2∂b2∂L=δ2

步骤3：计算隐藏层误差梯度δ1\delta_1δ1（损失对隐藏层加权和的偏导）

原始展开式（链式法则）

δ1=∂L∂z1=∂L∂z2⋅∂z2∂a1⋅∂a1∂z1\delta_1 = \frac{\partial L}{\partial z_1} = \frac{\partial L}{\partial z_2} \cdot \frac{\partial z_2}{\partial a_1} \cdot \frac{\partial a_1}{\partial z_1}δ1=∂z1∂L=∂z2∂L⋅∂a1∂z2⋅∂z1∂a1

损失L对z1z_1z1的梯度，需要经过"损失→z2z_2z2→a1a_1a1→z1z_1z1"的三层传递，体现链式法则的多层级特性。

代入各局部导数

1. 损失对z2z_2z2的梯度：∂L∂z2=δ2\frac{\partial L}{\partial z_2} = \delta_2∂z2∂L=δ2（复用步骤1的结果）；
2. z2z_2z2对a1a_1a1的梯度：∂z2∂a1=w2\frac{\partial z_2}{\partial a_1} = w_2∂a1∂z2=w2（z2=w2a1+b2z_2 = w_2a_1 + b_2z2=w2a1+b2，对a1a_1a1求导，乘法节点特性：固定w2w_2w2，导数为w2w_2w2）；
3. 隐藏层输出对z1z_1z1的梯度：∂a1∂z1=σ′(z1)=a1(1−a1)\frac{\partial a_1}{\partial z_1} = \sigma'(z_1) = a_1(1 - a_1)∂z1∂a1=σ′(z1)=a1(1−a1)（sigmoid激活函数的导数特性）。

简化合并项

δ1=δ2⋅w2⋅a1(1−a1)\delta_1 = \delta_2 \cdot w_2 \cdot a_1(1 - a_1)δ1=δ2⋅w2⋅a1(1−a1)
δ1\delta_1δ1是隐藏层的"误差梯度"，代表损失L随隐藏层加权和z1z_1z1变化的速率，是计算隐藏层参数梯度的核心中间量。

步骤4：计算隐藏层参数（w1、b1w_1、b_1w1、b1）的梯度

4.1 隐藏层权重w1w_1w1的梯度

原始展开式（链式法则）

∂L∂w1=∂L∂z1⋅∂z1∂w1\frac{\partial L}{\partial w_1} = \frac{\partial L}{\partial z_1} \cdot \frac{\partial z_1}{\partial w_1}∂w1∂L=∂z1∂L⋅∂w1∂z1

损失L对w1w_1w1的梯度，等于损失对z1z_1z1的梯度（即δ1\delta_1δ1），乘以z1z_1z1对w1w_1w1的梯度。

代入各局部导数

1. 损失对z1z_1z1的梯度：∂L∂z1=δ1\frac{\partial L}{\partial z_1} = \delta_1∂z1∂L=δ1（已在步骤3算出，直接复用）；
2. z1z_1z1对w1w_1w1的梯度：∂z1∂w1=x\frac{\partial z_1}{\partial w_1} = x∂w1∂z1=x（z1=w1x+b1z_1 = w_1x + b_1z1=w1x+b1，对w1w_1w1求导，乘法节点特性：固定x，导数为x）。

简化合并项

∂L∂w1=δ1⋅x\frac{\partial L}{\partial w_1} = \delta_1 \cdot x∂w1∂L=δ1⋅x

4.2 隐藏层偏置b1b_1b1的梯度

原始展开式（链式法则）

∂L∂b1=∂L∂z1⋅∂z1∂b1\frac{\partial L}{\partial b_1} = \frac{\partial L}{\partial z_1} \cdot \frac{\partial z_1}{\partial b_1}∂b1∂L=∂z1∂L⋅∂b1∂z1

损失L对b1b_1b1的梯度，等于损失对z1z_1z1的梯度，乘以z1z_1z1对b1b_1b1的梯度。

代入各局部导数

1. 损失对z1z_1z1的梯度：∂L∂z1=δ1\frac{\partial L}{\partial z_1} = \delta_1∂z1∂L=δ1（复用步骤3的结果）；
2. z1z_1z1对b1b_1b1的梯度：∂z1∂b1=1\frac{\partial z_1}{\partial b_1} = 1∂b1∂z1=1（z1=w1x+b1z_1 = w_1x + b_1z1=w1x+b1，对b1b_1b1求导，加法节点特性：固定其他项，导数为1）。

简化合并项

∂L∂b1=δ1\frac{\partial L}{\partial b_1} = \delta_1∂b1∂L=δ1

加法节点特性

加法节点输出：z=x+yz = x + yz=x+y（x、y为输入，z为输出）

偏导数目标：计算 ∂z∂x\frac{\partial z}{\partial x}∂x∂z 和 ∂z∂y\frac{\partial z}{\partial y}∂y∂z

导数的极限定义：∂z∂t=lim⁡Δt→0z(t+Δt)−z(t)Δt\frac{\partial z}{\partial t} = \lim_{\Delta t \to 0} \frac{z(t+\Delta t) - z(t)}{\Delta t}∂t∂z=limΔt→0Δtz(t+Δt)−z(t)

（1）计算 ∂z∂x\frac{\partial z}{\partial x}∂x∂z

固定y为常数（比如y=3），输入x的变化量为Δx\Delta xΔx：

原输出：z(x)=x+3z(x) = x + 3z(x)=x+3

变化后输出：z(x+Δx)=(x+Δx)+3=x+3+Δxz(x+\Delta x) = (x+\Delta x) + 3 = x + 3 + \Delta xz(x+Δx)=(x+Δx)+3=x+3+Δx

函数变化量：z(x+Δx)−z(x)=(x+3+Δx)−(x+3)=Δxz(x+\Delta x) - z(x) = (x+3+\Delta x) - (x+3) = \Delta xz(x+Δx)−z(x)=(x+3+Δx)−(x+3)=Δx

求极限：∂z∂x=lim⁡Δx→0ΔxΔx=1\frac{\partial z}{\partial x} = \lim_{\Delta x \to 0} \frac{\Delta x}{\Delta x} = 1∂x∂z=limΔx→0ΔxΔx=1

（2）计算 ∂z∂y\frac{\partial z}{\partial y}∂y∂z

固定x为常数（比如x=5），输入y的变化量为Δy\Delta yΔy：

原输出：z(y)=5+yz(y) = 5 + yz(y)=5+y

变化后输出：z(y+Δy)=5+(y+Δy)=5+y+Δyz(y+\Delta y) = 5 + (y+\Delta y) = 5 + y + \Delta yz(y+Δy)=5+(y+Δy)=5+y+Δy

函数变化量：z(y+Δy)−z(y)=(5+y+Δy)−(5+y)=Δyz(y+\Delta y) - z(y) = (5+y+\Delta y) - (5+y) = \Delta yz(y+Δy)−z(y)=(5+y+Δy)−(5+y)=Δy

求极限：∂z∂y=lim⁡Δy→0ΔyΔy=1\frac{\partial z}{\partial y} = \lim_{\Delta y \to 0} \frac{\Delta y}{\Delta y} = 1∂y∂z=limΔy→0ΔyΔy=1

乘法节点特性

乘法节点输出：z=m×nz = m \times nz=m×n（m、n为输入，z为输出）

偏导数目标：计算 ∂z∂m\frac{\partial z}{\partial m}∂m∂z 和 ∂z∂n\frac{\partial z}{\partial n}∂n∂z

2. 偏导数推导（基于极限定义）

（1）计算 ∂z∂m\frac{\partial z}{\partial m}∂m∂z

固定n为常数（比如n=6），输入m的变化量为Δm\Delta mΔm：

原输出：z(m)=m×6=6mz(m) = m \times 6 = 6mz(m)=m×6=6m

变化后输出：z(m+Δm)=(m+Δm)×6=6m+6Δmz(m+\Delta m) = (m+\Delta m) \times 6 = 6m + 6\Delta mz(m+Δm)=(m+Δm)×6=6m+6Δm

函数变化量：z(m+Δm)−z(m)=(6m+6Δm)−6m=6Δmz(m+\Delta m) - z(m) = (6m+6\Delta m) - 6m = 6\Delta mz(m+Δm)−z(m)=(6m+6Δm)−6m=6Δm

求极限：∂z∂m=lim⁡Δm→06ΔmΔm=6=n\frac{\partial z}{\partial m} = \lim_{\Delta m \to 0} \frac{6\Delta m}{\Delta m} = 6 = n∂m∂z=limΔm→0Δm6Δm=6=n

（2）计算 ∂z∂n\frac{\partial z}{\partial n}∂n∂z

固定m为常数（比如m=4），输入n的变化量为Δn\Delta nΔn：

原输出：z(n)=4×n=4nz(n) = 4 \times n = 4nz(n)=4×n=4n

变化后输出：z(n+Δn)=4×(n+Δn)=4n+4Δnz(n+\Delta n) = 4 \times (n+\Delta n) = 4n + 4\Delta nz(n+Δn)=4×(n+Δn)=4n+4Δn

函数变化量：z(n+Δn)−z(n)=(4n+4Δn)−4n=4Δnz(n+\Delta n) - z(n) = (4n+4\Delta n) - 4n = 4\Delta nz(n+Δn)−z(n)=(4n+4Δn)−4n=4Δn

求极限：∂z∂n=lim⁡Δn→04ΔnΔn=4=m\frac{\partial z}{\partial n} = \lim_{\Delta n \to 0} \frac{4\Delta n}{\Delta n} = 4 = m∂n∂z=limΔn→0Δn4Δn=4=m

神经网络场景（加法+乘法组合）

以加权和 z=wx+bz = wx + bz=wx+b（w=2，x=5，b=3）为例，拆解为"乘法节点+加法节点"的组合计算：

1. 乘法节点：z1=w×x=2×5=10z_1 = w \times x = 2×5 = 10z1=w×x=2×5=10
   偏导数：∂z1∂w=5\frac{\partial z_1}{\partial w}=5∂w∂z1=5，∂z1∂x=2\frac{\partial z_1}{\partial x}=2∂x∂z1=2（计算过程同上）；
2. 加法节点：z=z1+b=10+3=13z = z_1 + b = 10 + 3 = 13z=z1+b=10+3=13
   偏导数：∂z∂z1=1\frac{\partial z}{\partial z_1}=1∂z1∂z=1，∂z∂b=1\frac{\partial z}{\partial b}=1∂b∂z=1（计算过程同上）；
3. 组合偏导数（链式法则）：
   ∂z∂w=∂z∂z1×∂z1∂w=1×5=5\frac{\partial z}{\partial w} = \frac{\partial z}{\partial z_1} \times \frac{\partial z_1}{\partial w} = 1×5 = 5∂w∂z=∂z1∂z×∂w∂z1=1×5=5；
   数值验证：w从2→3，z=3×5+3=18，变化量=18-13=5，变化率=5/1=5。

可视化代码

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Circle, FancyArrowPatch
from math import atan2, cos, sin

# 配置LaTeX渲染（若环境不支持可注释）
plt.rcParams['text.usetex'] = True

# 创建画布
fig, ax = plt.subplots(figsize=(12, 8))
ax.set_xlim(0, 12)
ax.set_ylim(0, 8)
ax.axis('off')

# 定义各层x坐标（输入层、隐藏层、输出层、输出箭头终点）
layer_x = [2.0, 5.5, 8.5, 10.8]  
# 神经元半径（统一）
neuron_radius = 0.5

# ===================== 1. 输入层（无参数，单节点） =====================
input_y = [4.0]  # 单输入节点
for i, y in enumerate(input_y):
    circle = Circle((layer_x[0], y), neuron_radius, fill=True, color='lightgray', ec='black', lw=1.5)
    ax.add_patch(circle)
    ax.text(layer_x[0], y, r'$x$', ha='center', va='center', fontsize=16)

# ===================== 2. 隐藏层（1层，单节点，Sigmoid激活） =====================
hidden_y = [4.0]  # 单隐藏层节点
for i, y in enumerate(hidden_y):
    circle = Circle((layer_x[1], y), neuron_radius, fill=True, color='lightgreen', ec='black', lw=1.5)
    ax.add_patch(circle)
    ax.text(layer_x[1], y, r'$a_1^{(1)}$', ha='center', va='center', fontsize=16)

# ===================== 3. 输出层（1层，单节点，恒等激活） =====================
output_y = [4.0]  # 单输出节点
for i, y in enumerate(output_y):
    circle = Circle((layer_x[2], y), neuron_radius, fill=True, color='lightpink', ec='black', lw=1.5)
    ax.add_patch(circle)
    ax.text(layer_x[2], y, r'$a_1^{(2)}$', ha='center', va='center', fontsize=16)
    
    # 输出箭头（指向预测值ŷ，终点在圆边缘）
    arrow_start_x = layer_x[2] + neuron_radius
    arrow = FancyArrowPatch((arrow_start_x, y), (layer_x[3] - 0.6, y),
                            arrowstyle='->', mutation_scale=20, lw=2, color='black')
    ax.add_patch(arrow)
    ax.text(layer_x[3], y, r'$\hat{y}$', ha='center', va='center', fontsize=16)

# ===================== 4. 绘制层间连接（仅连接到神经元边缘，不穿入） =====================
def draw_connections(x1, y1s, x2, y2s, radius, color='gray', alpha=0.6, lw=1.5):
    """
    绘制层间连接线，避免穿入神经元内部
    :param x1: 起始层x坐标
    :param y1s: 起始层节点y坐标列表
    :param x2: 目标层x坐标
    :param y2s: 目标层节点y坐标列表
    :param radius: 神经元半径
    """
    for y1 in y1s:
        for y2 in y2s:
            # 计算连线的角度（从起始点到目标点）
            dx = x2 - x1
            dy = y2 - y1
            angle = atan2(dy, dx)
            
            # 起始点：从圆心向外偏移半径（避免穿入起始神经元）
            start_x = x1 + radius * cos(angle)
            start_y = y1 + radius * sin(angle)
            
            # 目标点：向圆心偏移半径（避免穿入目标神经元）
            end_x = x2 - radius * cos(angle)
            end_y = y2 - radius * sin(angle)
            
            # 绘制连接线
            ax.plot([start_x, end_x], [start_y, end_y], color=color, alpha=alpha, lw=lw, zorder=1)

# 绘制输入→隐藏层、隐藏→输出层的连接
draw_connections(layer_x[0], input_y, layer_x[1], hidden_y, neuron_radius)
draw_connections(layer_x[1], hidden_y, layer_x[2], output_y, neuron_radius)

# ===================== 5. 层标题与参数标注 =====================
ax.text(layer_x[0], 6.5, 'Input Layer', ha='center', fontsize=18, fontweight='bold')
ax.text(layer_x[1], 6.5, 'Hidden Layer\n(Sigmoid)', ha='center', fontsize=18, fontweight='bold')
ax.text(layer_x[2], 6.5, 'Output Layer\n(Identity)', ha='center', fontsize=18, fontweight='bold')

# 权重/偏置标注
ax.text((layer_x[0] + layer_x[1])/2, 5.8, r'$\mathbf{W}^{(1)}, \mathbf{b}^{(1)}$', 
        ha='center', fontsize=14, color='darkblue', fontweight='bold')
ax.text((layer_x[1] + layer_x[2])/2, 5.8, r'$\mathbf{W}^{(2)}, \mathbf{b}^{(2)}$', 
        ha='center', fontsize=14, color='darkblue', fontweight='bold')

# 调整布局并显示
plt.tight_layout()
plt.show()

# 可选保存
# plt.savefig('2layer_neural_network_no_inside_line.pdf', bbox_inches='tight', dpi=300)
# plt.savefig('2layer_neural_network_no_inside_line.png', bbox_inches='tight', dpi=300)